基于组合代理模型的箱形梁轻量化设计*

陈 杨 秦义校 杨俊乐

太原科技大学机械工程学院 太原 030024

0 引言

由于复杂工程问题的有限元建模时间和求解时间过长，且在寻优过程中需要大量的仿真数据，会使复杂工程问题的寻优耗费大量时间。针对此问题，研究人员迫切需要一种能够高效求解工程问题的代理模型，使复杂工程问题的寻优得到合理的解决方法。

代理模型又称为元模型或响应面模型，是基于少量数据而构建的一种真实模型的模型，即模型的模型，具有结构简单、计算效率高等特点[1]。最常用的代理模型包括多项式响应面（Respones Surface methodology，RSM）、Kriging 模型、径向基（Radial Bssis Function，RBF）函数等，很多学者针对代理模型的精确问题进行了研究[2]，并对RSM、Kriging 和RBF这3 种代理模型进行了对比[3-5]，在实际工程中验证了其优越性[6]。

针对箱形梁、薄板结构的优化主要集中在轻量化设计和对加强筋的优化（如利用有限元软件对桥式起重机合理、轻量化、节能化的箱形梁结构等）[7]。Pinca C B等[8]利用Cosmos/M 有限元软件对冶金起重机的箱形梁截面进行轻量化设计；Abid M 等[9]针对桥式起重机箱形梁中加强筋的个数、形状、位置进行优化，并优化了箱形梁的截面形状，以获得最大的允许弯曲应力；Zhang H 等[10]将函数逼近法与梯度下降法结合，通过对加强筋布局位置的优化，提出了一种非对称的加强筋布局形式；Putra G L 等[11]提出了一种混合遗传算法（GA）对船舶结构的加强筋数量、类型以及加强筋间距和板厚进行优化，得到了更加轻量化的船舶结构；Ehsani A 等[12]提出针对薄板结构的轻量化问题，提出了一种格栅结构的可变肋板模型（VRM）找到网格板的最佳布局方式。

本文针对桥式起重机箱形梁结构进行轻量化设计，首先建立了有限元模型确定箱形梁各部位的优化变量[13]，利用最优拉丁超立方对设计变量抽样，并对RSM、RBF 和Kriging 这3 种代理模型进行拟合和插值[14]。其次，对得到的3 种代理模型进行误差分析。最后，提出了一种基于代理模型和自适应模拟退火算法（Adaptive Simulated Annealing，ASA）以及序列二次规划法（Sequence Quadratic Programing，SQP）相结合的优化策略，对3 种模型在满足强度、刚度和稳定性条件下进行轻量化设计。

1 目标函数及约束条件

桥式起重机的箱形梁通常在高温、重载等恶劣环境中工作。由于箱形梁一般为细长结构，在弯扭、屈曲变形作用下容易产生局部失稳和开裂，从而对桥式起重机的正常运行产生影响。因此，对箱形梁的结构进行优化布局，进而得到更好的力学性能是十分必要的[15，16]。

为了得到更加合理的布局形式，本文以箱形梁跨中最大应力为验证条件，即目标函数为最小化跨中最大应力。在实际情况下，布局方式与箱形梁跨中最大应力是高度非线性方程，代理模型能够模拟这种黑盒特性及计算复杂性。为便于箱形梁的各个部位优化，本文对各个优化部位进行归一化操作，优化结束后再反归一化得到对应的优化结果。

如图1 所示，本文的设计变量共有9 个，各个优化部位用 替代整个优化过程，其中X＝[x1，x2，x3，…，x9]T。x1和x2为主腹板和副腹板的厚度，x3为隔板的厚度，x4和x5为上翼缘板和下翼缘板的厚度，x6为上下翼缘板的间距，x7为腹板的间距，x8和x9为隔板孔宽和隔板孔长。

图1 桥式起重机箱形梁变量设计图

本文用G1（X）表示设计变量与跨中最大应力，箱形梁的变形同样采用代理模型进行模拟，用G2（X）表示设计变量与跨中最大变形的关系，优化前箱形梁满载时跨中最大应力σmax＝200.69 MPa，跨中最大变形Ymax＝20.02 mm，由起重机设计准则可得约束条件。

1）强度条件

式中：G1（X）为变量跨中最大应力，σs为材料屈服强度，σb为材料抗拉强度。

2）刚度条件

式中：G2（X）为变量跨中最大变形，[Y]为箱形梁的许用变形。

最终得到的优化方程为

式中：G1（X）为目标函数，G2（X）为约束条件，Lb[X]为变量的下界，Ub[X]为变量的上界。

为了在优化布局方式的同时不使模型质量增加，加入质量条件约束，设优化前的质量为Mt，优化后的质量为M，则有

2 组合代理模型全局优化算法

本文采用自适应模拟退火算法（ASA）与序列二次规划法（SQP）相结合的算法（即ASA-SQP 算法），以此得到箱形梁的最佳布局方式。模拟退火算法是模拟金属热态加工过程而发展的算法，与遗传算法有很多相似之处。模拟退火算法比遗传算法更易于实现，因为其在每次搜索空间只检查1 个设计点，而遗传算法对1 组寻优点进行寻优。模拟退火算法的基本思路是从初始点开始对目标函数进行评估，函数值下降，新的寻优点即可被接受，如此反复直至找到最优点。为了避免陷入局部最优，根据Metropolis 判断准则函数值上升的点亦可被接受。自适应模拟退火算法具有比模拟退火算法更强大的全局寻优能力和计算效率，为了加速其在找到全局最优解最近的寻优速度，引入了梯度算法（序列二次规划法）有更强的局部寻优能力。

序列二次规划法（SQP）是将目标函数进行二次泰勒级数展开，并将约束条件线性化，通过解二次规划得到下一个设计点，然后根据2 个可供选择的优化函数执行一次线性搜索，其中Hessian 矩阵由BFGS 公式更新。

代理模型的建模首先需要对样本空间进行抽样，目前常见的抽样方法为拉丁超立方设计(Latin Hypercube Design，LHD)，其原理是在n维设计空间中，将每一维坐标区间［xkmin，xkmax］，k∈［1，n］均匀地等分成m个区间，每个小区间被记为随机选取m个点，保证一个因子的每个水平只被研究1 次，即构成维度为n，样本数为m的拉丁超立方设计，记为m×nLHD。

拉丁超立方设计比传统试验设计能够更好地布满整个设计空间，但仍可能存在试验点分布不够均匀、丢失设计区域的情况。最优拉丁超立方设计(Optimal Latin Hypercube Design，OLHD)改善了拉丁超立方设计的均匀性，使因子和响应的拟合更精确真实，图2 为最优拉丁超立方设计能生成更均匀样本点的分布情况。

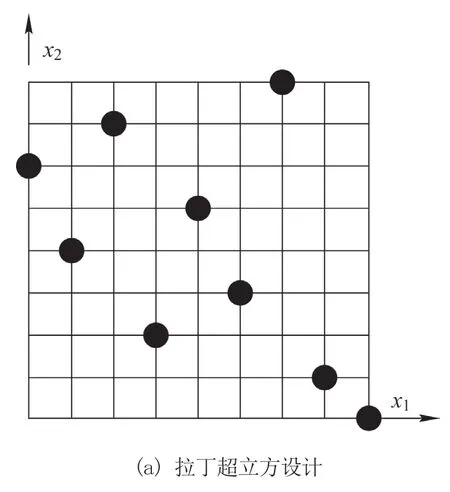
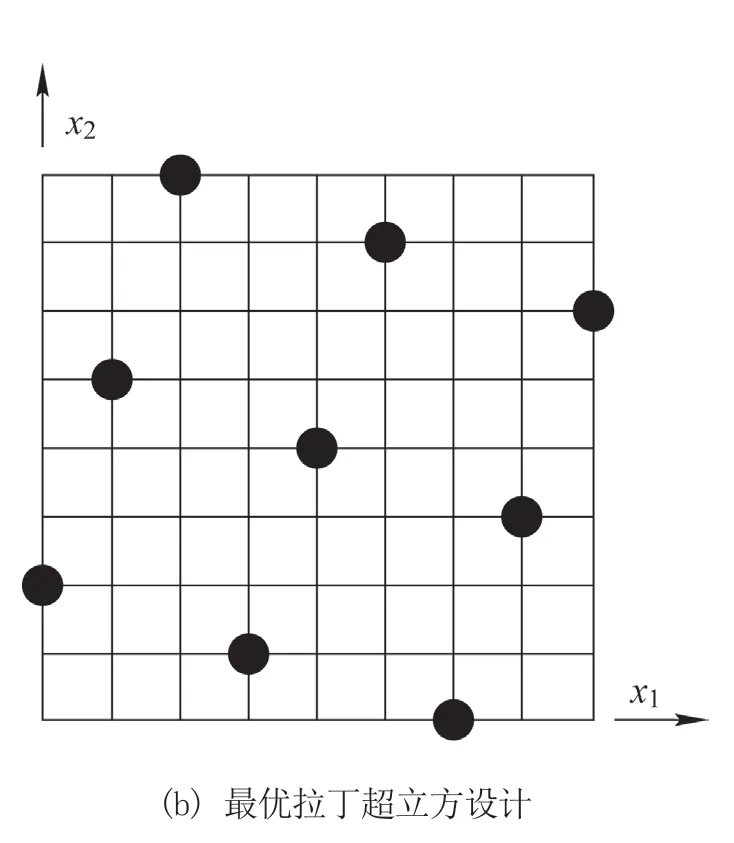
图2 最优拉丁超立方设计对比示意图

本文的优化流程分为建模和优化2 个模块。首先确定优化变量并对其进行参数化建模；其次利用最优拉丁超立方设计对设计变量进行优化，为了得到更好拟合效果，对优化变量进行归一化操作，并在设计空间内随机生成200 个样本点；然后对3 种代理模型分别进行拟合、插值，在设计空间中随机生成50 个误差样本点，对误差进行分析；最后，利用ASA-SQP 算法对3 种代理模型进行优化，并将优化结果与数值仿真进行对比验证，得到最终优化结果。

为了更好地评估3 种不同代理模型的建模精度，采用相同的样本点和误差点对3 种代理模型进行误差评估，工程上常用的代理模型误差分析准则为确定系数R2，即

式中：m为新随机生成的验证点个数，yi为验证点上的真实值，为代理模型生成的替代值，为平均值。

确定系数R2是一种直观反映模型预测能力的评价标准，也是使用最多的一种误差判断准则，其值越接近1 表示预测模型与真实值越接近。一般地，当R2＞0.9 时，代理模型的拟合效果有效。

在约束条件中，共有3 个输出变量，分别是质量Mass、最大应力Maxs 和跨中最大位移Maxu，此时3个输出变量在3 个代理模型下的确定系数如图3 所示。

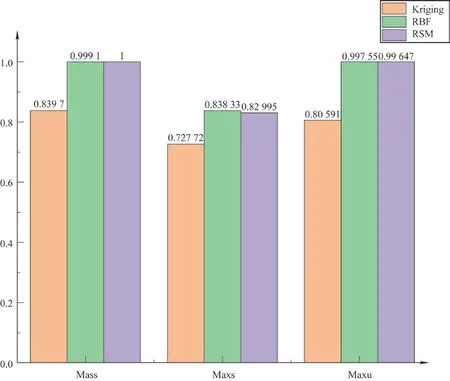
图3 3 个输出变量的确定系数

由图3 可知，Kriging 模型对3 个变量的代理均不符合确定系数的要求，而代理模型RBF、RSM 在Mass和Maxu 上的代理效果趋近于1，而在最大应力上也不符合确定系数的要求。

由有限元软件中改变输入变量可知，最大应力随变量的改变其位置也发生改变，而代理模型的代理效果往往只针对于某一个区域的最大应力，如箱形梁的最大变形总发生于跨中，故其代理效果往往尚佳。对有限元模型进一步分析，可知箱形梁的最大应力基本发生在跨中下盖板及2 个端梁处，如图4 所示。

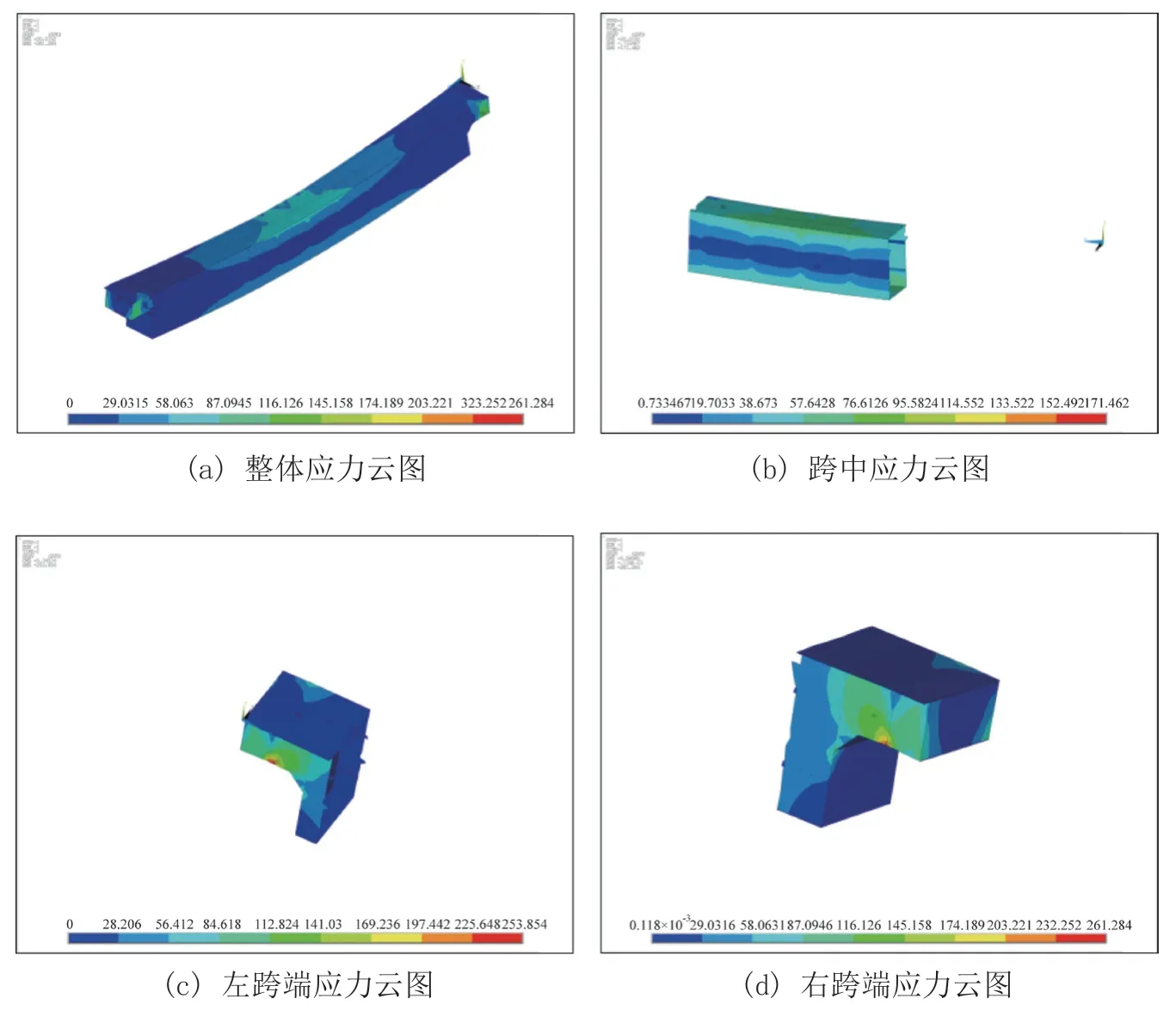
图4 优化前应力云图

综上所述，为了得到更好代理效果，将Maxs 变量替换为跨中下盖板及2 个端梁处的最大应力，分别表示为Maxs_1、Maxs_2、Maxs_3，重复上述代理模型舍弃掉Kriging 模型，得到的确定系数R2如图5 所示。

图5 确定系数R2

由图5 可知，通过添加代理变量，RBF 和RSM 在5 个代理变量下均达到确定系数许用要求。然而为了得到更好代理效果，从5 个变量确定系数的绝对大小分别看，提出一种组合代理模型，即Mass 和Maxs_1 采用RSM 代理，而Maxs_2、Maxs_3 和Maxu 变量采用RBF 代理，得到一种组合代理模型RSM-RBF。

3 优化算法

利用ASA-SQP 算法对3 种代理模型进行优化，并将优化结果与数值仿真进行对比验证，得到最终优化结果。对RSM、RBF 和RSM-RBF 这3 种代理模型进行优化得到迭代图像如图6 所示，3 种代理模型优化结果与有限元的对比如表1 所示。

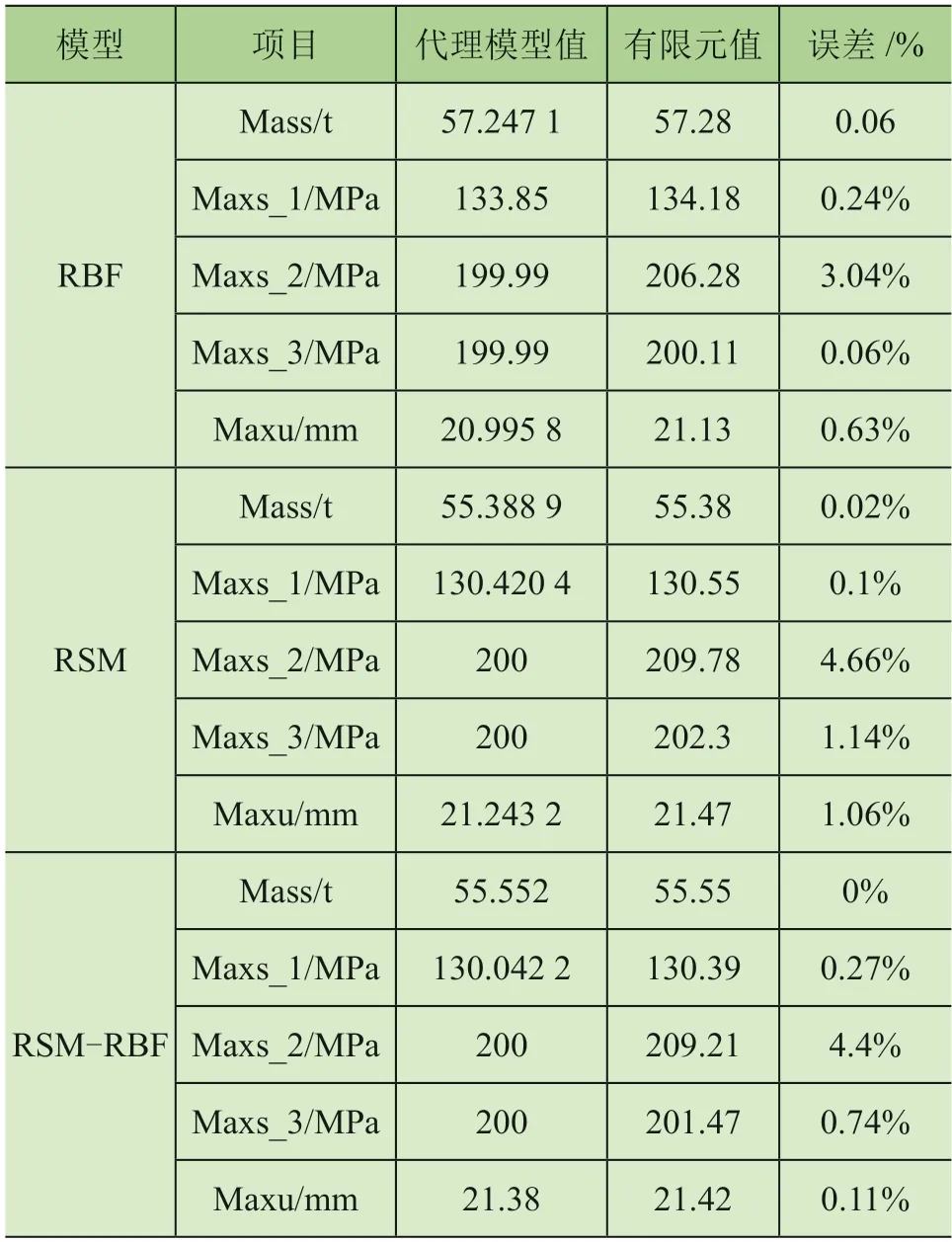
表1 各代理模型优化对比

图6 收敛迭代图

由表1 可知，基于RBF 得到的最小质量最大，但其在Maxs_2、Maxs_3 以及Maxu 这3 个变量的误差要显著小于RBF代理模型，这与确定系数的误差判断一致。RSM 以及RSM-RBF 这2 种代理模型优化得到的质量相差无几，但RSM-RBF 代理5 个变量与有限元结果进行对比所得到的综合误差要优于组合变量之前的两种单独代理模型的误差。综上，本文最终采用RSM-RBF 组合代理模型作为本文最终优化所用的模型。

4 优化结果

各部分的优化结果如表2 所示，所得到优化后的质量为55.33 t，相比于优化前的65.54 t，箱形梁的质量降低了15.59%。

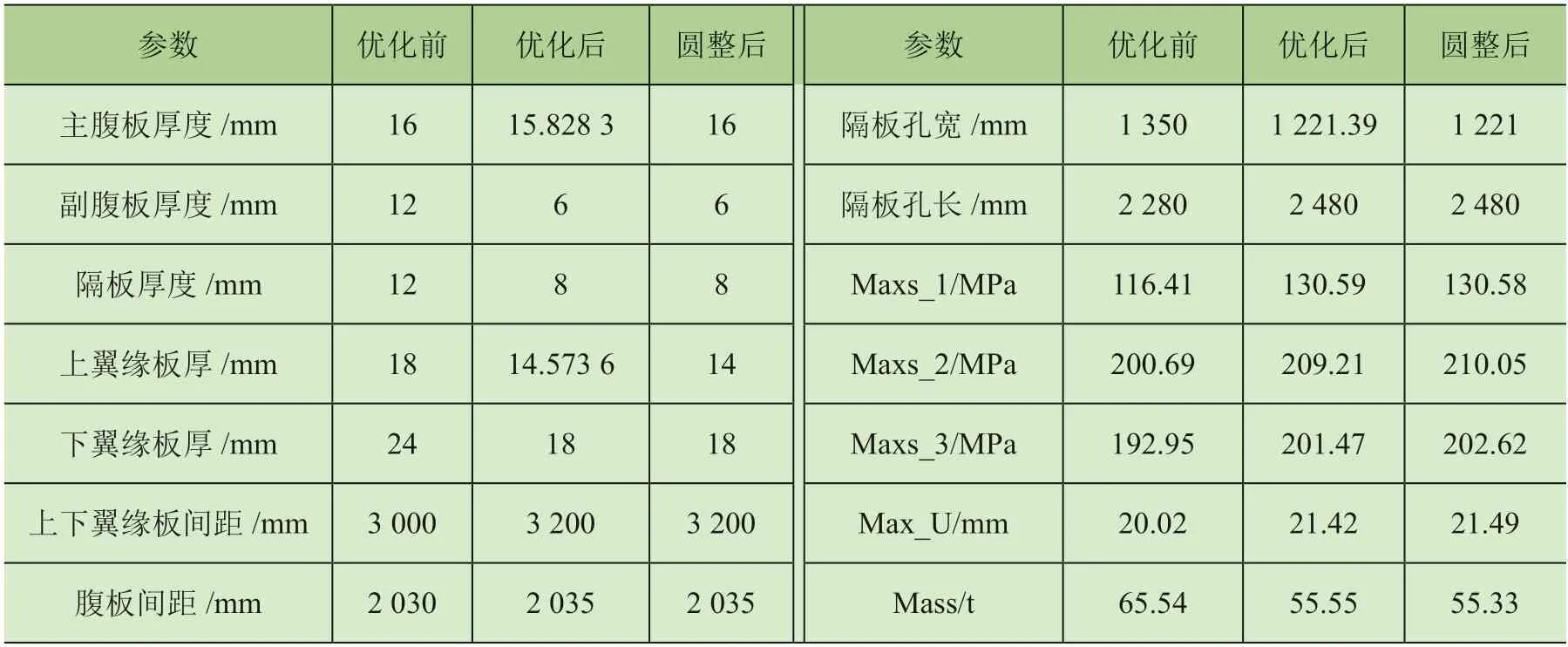
表2 各代理模型优化对比

其优化后的应力云图7 所示，结果符合强度、刚度条件。

图7 优化后的应力云

5 结论

本研究针对工程优化中常用的3 种代理模型，即多项式响应面（RSM）、RBF 神经网络和Kriging 模型进行了比较研究，对桥式起重机的进行轻量化设计。通过对3 种代理模型在确定系数R2的误差分析，按子结构进行分块代理达到了更好的代理效果，根据不同代理模型的代理效果，提出了RSM-RBF 组合代理模型。最后，利用一种智能与梯度组合算法对3 种代理模型进行优化，并将优化结果与有限元分析结果进行对比.结果显示，RSM-RBF 组合代理模型有更好的误差代理效果，且其寻优结果使得质量降低了15.59%，证明了改优化策略具有与一定的工程价值。