基于空间干涉成像的七芯光纤芯间群延时差测量
沈立翠,黄素娟,陈伟,闫成,赵欣鹏
(上海大学 通信与信息工程学院, 特种光纤与光接入网重点实验室,上海 200444)
0 引言
使用多芯光纤(Multicore Fiber, MCF)的不同纤芯作为独立并行的空间通道来传输不同信息,可解决传统单模光纤(Single Mode Fiber, SMF)的传输容量限制问题。近年来,MCF 已经成为空分复用(Space-Division Multiplexing, SDM)系统[1-5]和微波光子学(Microwave Photonics, MWP)领域[6-10]的重点研究对象。MCF 的芯间群延时差(Differential Group Delay, DGD)是一个关键的物理参数。在SDM 系统中MCF 的传播延时差太大会降低可实现的符号速率、传输距离,并增加接收器的设计和信号处理的复杂度[11,12]。在MWP 信号处理中,为了使MCF 作为可调谐采样(True-Time Delay Line, TTDL)工作,每个纤芯需要不同的群延时和色散特性,以实现光波长的可调谐性[13]。
目前MCF 的芯间群延时差的测量方法主要有:脉冲响应法、白光光谱干涉法、差分相移法以及光谱干涉法。2014 年,日本的SAKAMOTO T 等[14]使用脉冲响应法测量了四芯光纤的芯间群延时差,该方法测量精度较低,对脉冲信号质量要求高,且所需测量光纤长度较长,一般为几公里到几十公里。白光光谱干涉法是基于马赫-曾德尔干涉仪原理的测量方法。2015 年,LEE H J 等[15]使用两个空间光调制器将SMF 的基模与MCF 多个芯的模式任意相干叠加,以构成马赫-曾德尔型多径干涉仪,通过测量输出光谱的干涉条纹周期可推算出不同芯间折射率差,它可测量长度较短的MCF(1 m),但其实验装置复杂,对光路调节的精度要求很高。2020 年,SASAKI Y 等[16]使用差分相移法测量了四芯光纤的芯间群延时差,该方法可直接通过相位差获得任意两芯之间的延时差,但它需要对信号进行滤波、放大以及采样处理,测量成本较高,且数据处理复杂。2019 年,GARCíA S 等[17]使用光谱干涉法测量研究了弯曲对七芯光纤芯间群延时差的影响,该方法使用多芯光纤本身作为干涉仪,不需要搭建复杂的干涉仪,具有较好的抗干扰和环境变化的能力,但它对光谱仪的分辨率要求较高,且测量时需要使用光纤扇入扇出模块来实现单模光纤与多芯光纤之间的光源耦合,由于该模块本身就存在延时,会导致测量结果出现误差。
本文提出了基于空间干涉成像的多芯光纤芯间群延时差测量方法。多芯光纤中不同芯间的结构差异和弯曲都会引起不同芯的群延时存在差异,导致不同芯在激光下在空间上发生干涉。使用CCD 记录不同波长下的空间干涉图像,并从干涉图像中提取空间所有点的干涉光谱,通过光谱分析可获得多芯光纤芯间群延时差。
1 测量原理
对于沟槽辅助型弱耦合多芯光纤,其芯间距较大可忽略芯间耦合[18]。假设每个芯独立,则其任意一个芯m(m为纤芯的编号)中的导波模传输常数βm可表示为
式中,k0为真空中的波数,neff,m为芯m中导波模的有效折射率,nm为芯m的折射率,am为芯m的半径,U为阶跃折射率光纤的归一化横向相位参数,可通过求解光纤模式特征方程获得。将传播常数对角频率求导可得长度为L的多芯光纤中任意芯的群延时为[19]
在七芯光纤中当激光只耦合到中间纤芯与外围两个相邻的纤芯中时,由于不同芯具有不同群延时,在任意空间点(x,y)处三个芯会两两相干叠加发生干涉。令中间纤芯的编号为0,当使用系数An(x,y)(n=1,2,…,6)将中间芯与外围任意芯n的电场关联时可得[20]
式中,E0和En分别为中间芯和外围任意芯n的电场分布,Δτn是中间芯与外围任意芯n的芯间群延时差。中间芯与两个相邻的外围芯p 和芯q 相干叠加的总电场分布可表示为
则其总干涉光强可表示为
式中,I0(x,y,ω)为中间纤芯的导波模的光强分布。从式(5)中可看出,在多芯光纤出射端,空间中任意一点(x,y)处的干涉光强值随频率的变化而发生周期性的变化。因此,对式(5)关于角频率ω做傅里叶变换可得多芯光纤的芯间群延时差。
式中,F0(x,y,τ)是I0(x,y,ω)的傅里叶变换;等式右边第二项为中间芯与外围芯p 的干涉项,当τ=±Δτp时会产生一个尖峰,为两个芯中基模的光学拍;第三项为中间芯与外围芯q 的干涉项,在τ=±Δτq时有一个尖峰出现;第四项为外围芯p 和芯q 的芯间干涉项,在τ=±(Δτp-Δτq)时会出现一个尖峰。所以当同时激发多芯光纤的三个芯时由其干涉光谱经傅里叶变换取模值相加后可得三个包含芯间群延时差的尖峰,而当只激发两个芯,只有一个尖峰出现。
多芯光纤中的芯间群延时差不仅与光纤本身的结构有关,还受到弯曲的影响。相较于未弯曲时的纤芯有效折射率,由弯曲引起的纤芯有效折射率分布可表示为[21]
式中,neffb,m为芯m弯曲时的有效折射率,Rb为弯曲半径,(r,θ)是图1(a)中(x,y)笛卡尔坐标系对应的极坐标系。从式(7)可看出,当纤芯m和多芯光纤中心的连接线与曲率面形成的夹角θ=kπ,k∈Z时,由弯曲引起的有效折射率变化最大,而当,k∈Z时由弯曲引起的折射率变化为零,即弯曲时的有效折射率与未弯曲时的有效折射率相同。当七芯光纤沿x轴方向弯曲时,其由弯曲引起的纤芯的折射率变化如图1所示。根据式(7)可知,图1(a)中位于第一和第四象限的纤芯的有效折射率会变大,而位于第二和第三象限的纤芯的有效折射率则会变小。图1(b)展示了纤芯0、2 和5 在弯曲及未弯曲时的折射率分布对比,图中直线表示的是未弯曲时的纤芯折射率分布,虚线表示弯曲时的折射率分布。可看出当多芯光纤弯曲时,位于二、三象限的纤芯5 的折射率变小,而位于一、四象限的纤芯2 的折射率变大。
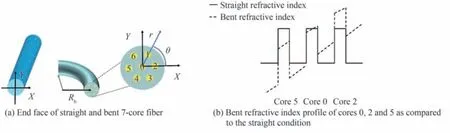
图1 弯曲对多芯光纤纤芯折射率的影响Fig. 1 Influence of bending on refractive index of multi-core fiber
当纤芯的有效折射率发生变化时,纤芯群延时也会随之变化,将式(7)带入式(2)可得弯曲时的纤芯群延时为
因此由弯曲引起的纤芯群延时变化可表示为
由式(9)可看出,由弯曲引起的纤芯群延时变化与弯曲半径成反比,因此大弯曲半径有助于降低弯曲对多芯光纤纤芯群延时的影响。与式(7)类似,式(9)中当纤芯m和多芯光纤中心的连接线与曲率面形成的夹角θ=kπ,k∈Z时由弯曲引起的纤芯群延时变化最大,而当θ=π/2+kπ,k∈Z时由弯曲引起的纤芯群延时变化为零。
2 实验装置
基于空间干涉成像的多芯光纤芯间群延时差测量实验装置如图2 所示,主要由可调谐激光器(Santec TSL-710, 1 480-1 640 nm)、单模光纤(Corning SMF-28e)、准直器(1 550 nm)、透镜、三维调节台、待测多芯光纤、物镜(60×)以及CCD(Hamamatsu C10633-23, 950~1 700 nm)组成。可调谐激光器输出的光,通过光纤连接器被耦合进单模光纤,经准直器准直后通过透镜聚焦再注入到待测纤芯中。其中,准直器和透镜的主要作用是减小入射光束的发散角,降低光能量损失,提升光束的传输和耦合效率。首先将多芯光纤两端擦净切平后分别固定在三维调节台1 和2 上,将多芯光纤的输出端接入光路Ι,组成一个多芯光纤纤芯选择激发系统,当光注入多芯光纤后,调节三维调节台2,使得从CCD 上可观察到清晰的光斑图。然后调节三维调节台1,使得通过CCD 可观察到多芯光纤中待测纤芯的光斑图,而其余芯中几乎或完全无光场分布。当选择完待测纤芯后将光路转换到光路П,此时由于没有物镜的聚焦作用,待测纤芯的出射光处于发散的状态,且由于不同的纤芯具有不同的群延时,待测纤芯的出射光会在空间上相干叠加产生干涉。在多芯光纤出射端使用CCD 记录不同波长下的空间干涉图,并从空间干涉图中提取空间干涉光谱,通过光谱分析可获得任意相邻两芯之间的群延时差。
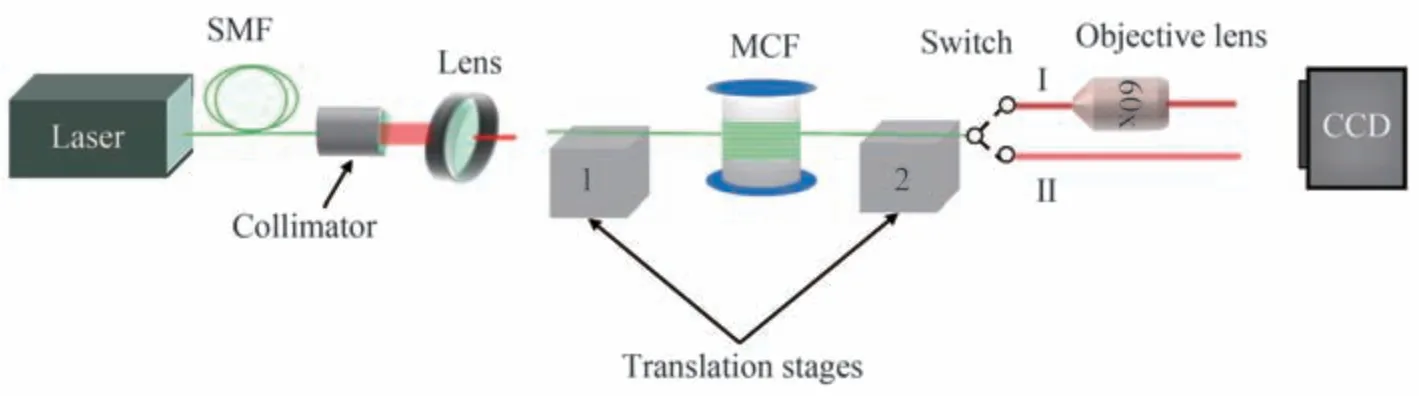
图2 基于空间干涉成像的多芯光纤芯间群延时差测量实验装置Fig. 2 Experimental setup for the measure of the DGD in a multi-core fiber
3 七芯光纤芯间延时差测量结果
测量选取的七芯光纤为每个芯都只传输基模的沟槽辅助型弱耦合多芯光纤,沟槽辅助型多芯光纤通过在纤芯周围引入低折射率沟道,将光场最大限度地束缚在纤芯内部,从而降低相邻纤芯的芯间串扰。图3(a)为沟槽辅助型多芯光纤每个芯的三维折射率分布示意图。图3(b)是所测七芯光纤在显微镜下的端面图,七芯光纤外围的六个芯均匀地分布在以中间芯为中心的正六边形上,其任意相邻两个芯的芯间距为36.64 μm,为弱耦合多芯光纤(一般芯间距在35~60 μm 之间),每个芯的直径为5.55 μm,内沟槽直径为17.90 μm,外沟槽直径为25.72 μm。测量光纤长度为50 m,光纤弯曲半径为75 mm,波长范围为1 548~1 552 nm(带宽为4 nm),波长间隔为0.01 nm。因此,每测量一组数据可采集401 张不同波长下的空间干涉图。
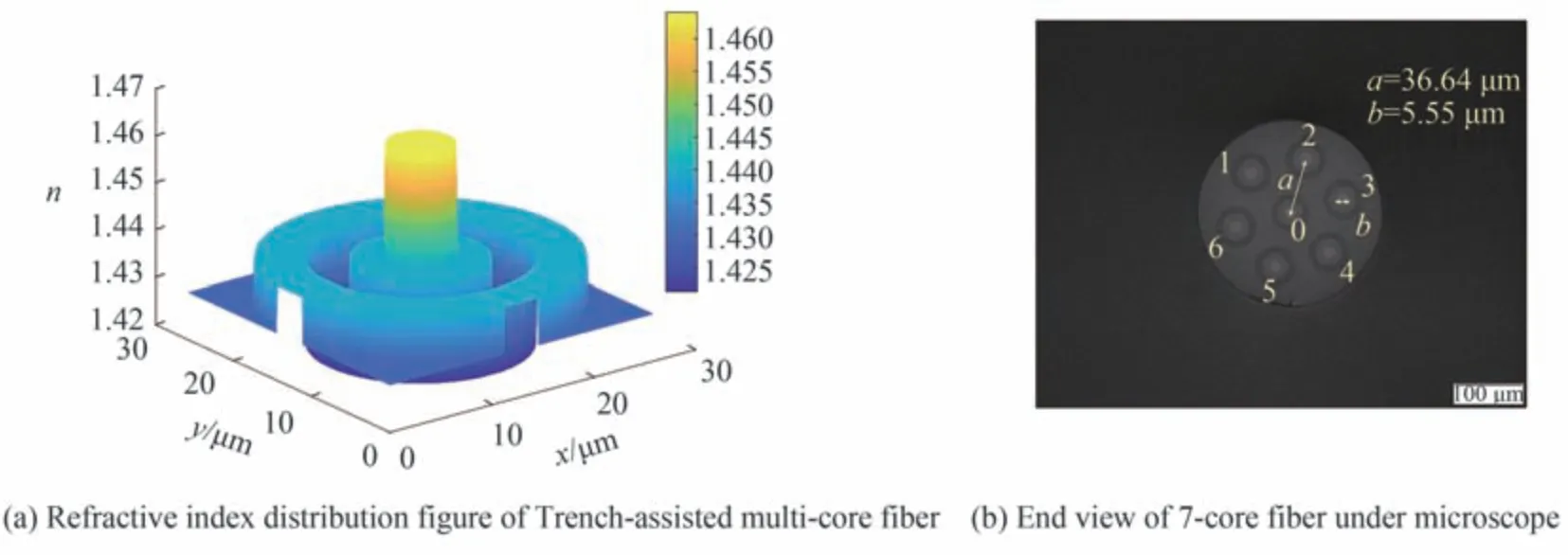
图3 沟槽辅助型多芯光纤Fig. 3 Trench-assisted multi-core fiber
当光只耦合到两个相邻的芯中时,结构参数的差异会导致两个芯之间存在群延时差。因此,在待测光纤的出射端面会在空间上发生干涉。测量时,观察CCD 并调节三维调节台来激发待测纤芯,而使其他芯保持未激发状态,图4(a)为在CCD 上观察到的只激发中间芯和纤芯1 时的情况。当完成待测纤芯的选择激发后,将光路转换到图2 中的光路Π,此时CCD 拍摄到的图像为两芯间的空间干涉图,图4(b)为CCD 采集到的401 张中间芯和芯1 的空间干涉图像,每张图片的分辨率为256×320,深度为14 bit。

图4 纤芯0 和纤芯1 的激发图及空间干涉图Fig. 4 Excitation diagram and spatial interference diagram of core 0 and core 1
图4(b)中,在每个波长下的空间干涉图中选取同一像素点(x,y),该点的光强随波长变化而变化,形成的振荡曲线为这个点的空间干涉光谱,图5(a)为像素点(110, 185)处的空间干涉光谱。将所有像素点的空间干涉光谱在空间上组合在一起可得如图5(b)所示的三维空间干涉光谱。

图5 纤芯0 和纤芯1 的空间干涉光谱Fig. 5 Spatial interference spectra of core 0 and core 1
对图5(a)的空间干涉光谱做傅里叶变换的结果如图6(a)所示,可看出除中间芯与芯1 的干涉尖峰外还有由噪声引起的尖峰,为了降低噪声的干扰,需要对图5(b)所示的所有点的空间干涉光谱同时做傅里叶变换,并将变换后的结果取模进行线性叠加,结果如图6(b)所示。从图6(b)中可看出由噪声产生的尖峰的能量远低于中间芯与芯1 干涉产生的尖峰的能量,由干涉产生的尖峰的横坐标的值为0.399 4 ps/m,为中间芯与芯1 的芯间群延时差。
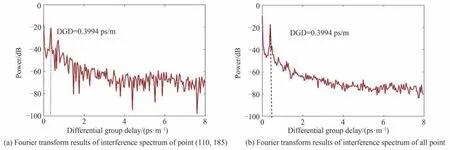
图6 纤芯0 与纤芯1 的空间干涉光谱分析结果Fig. 6 Spatial interference spectrum analysis results of cores 0, 1
同理,当依次同时激发中间芯和一个外围芯时通过对空间干涉图像提取的所有像素点的空间干涉光谱做傅里叶变换并取模相加,可获得七芯光纤的中间芯与外围六个芯的芯间群延时差,图7(a)和(b)分别是中间芯与芯2 以及中间芯和芯3 的光谱分析结果。从图中可知中间芯与芯2 的芯间群延时差为0.559 2 ps/m,中间芯与芯3 的芯间群延时差为0.439 4 ps/m。

图7 中间芯0 分别与外围芯2、芯3 的空间干涉光谱分析结果Fig. 7 Spatial interference spectrum analysis results of cores 0, 2 and cores 0, 3
从图6 和图7 的测量结果来看,中间芯和不同外围芯的芯间群延时差都各不相同,说明在七芯光纤中任意两个相邻外围芯的群延时也会存在差异。图7 中,将中间芯和芯2 以及中间芯和芯3 之间的芯间群延时差相减可获得芯2 和芯3 的芯间群延时差为0.119 8 ps/m。
除了测量中间芯与外围芯的芯间延时差,还可测量任意相邻两个外围芯的芯间延时差。测量时同时激发芯2 和芯3,而让其它芯保持未激发的状态。通过对两芯的空间干涉光谱进行光谱分析可获得两芯的芯间群延时差,分析结果如图8 所示。由图8 可知芯2 和芯3 的芯间群延时差为0.119 7 ps/m,与0.119 8 ps/m 相近,误差为1×10-4。
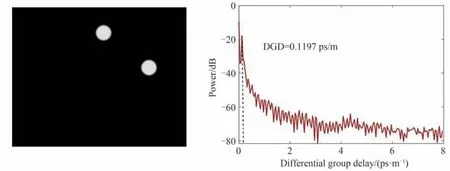
图8 同时激发纤芯2,3 时的空间干涉光谱分析结果Fig. 8 Spatial interference spectrum analysis results of core 2 and core 3
当同时激发三个纤芯时,相邻的芯会两两干涉,对干涉信息做傅里叶变换会出现三个干涉尖峰,图9 是同时激发纤芯0、2 和3 时的测量结果。
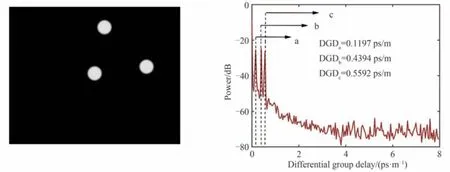
图9 同时激发纤芯0 和纤芯2,3 时的空间干涉光谱分析结果Fig. 9 Spatial interference spectrum analysis results of cores 0, 2 and 3
图9 中a、b、c 三点处的群延时差分别为0.119 7 ps/m、0.439 4 ps/m 以及0.559 2 ps/m,将图9 与图7 和图8对比可看出三个群延时差的值分别一一对应。因此,图9 中点a 的值是芯2 与芯3 的芯间群延时差,点b 和c的值分别是芯0 和芯3、芯2 的芯间群延时差。
同理,其它相邻芯之间也有相同的关系,表1 展示了中间芯与其余6 个外围芯、外围任意相邻两芯以及同时激发3 个芯时的芯间群延时差测量结果。
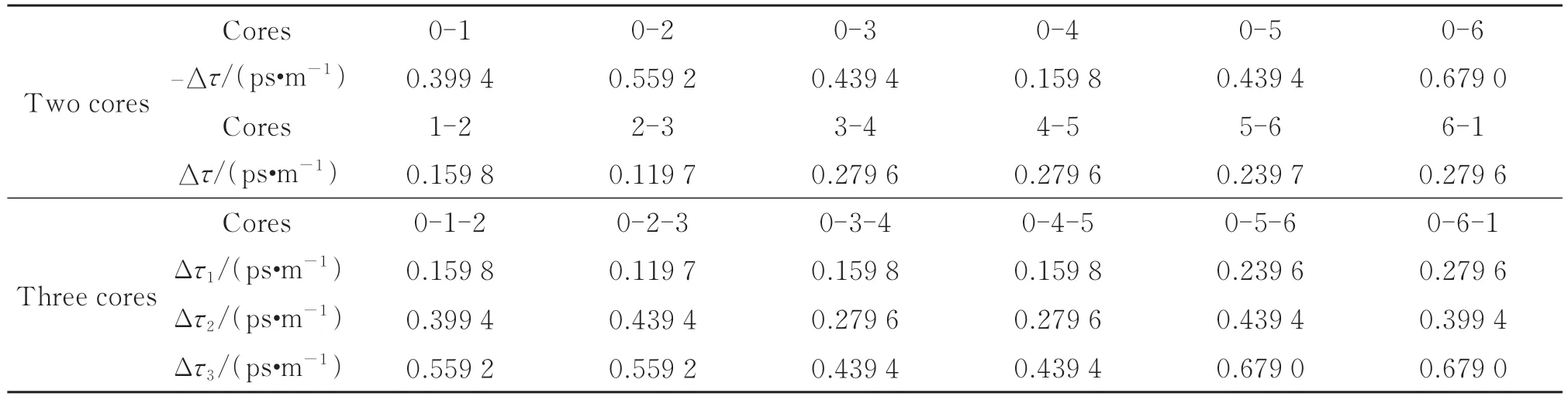
表1 七芯光纤芯间群延时差测量结果Table 1 Measurement results of the inter-core DGD of 7-core fiber
任意两个相邻外围芯的芯间群延时差可通过将中间芯分别与外围两个相邻芯的芯间群延时差相减获得,也可直接测量外围相邻两芯的芯间群延时差。对比表1 中的测量结果可发现任意两个相邻外围芯的芯间群延时差的直接测量结果与相减获得的结果相比,误差为1×10-4。同时激发三个互相相邻纤芯时的测量结果与单独激发两个芯时的测量结果都一一对应,与理论一致且验证了测量结果的准确性。
4 七芯光纤芯间延时差弯曲依赖性测量结果
为了研究七芯光纤芯间延时差的弯曲依赖性,分别测量了长度为50 m,弯曲半径为5 mm、75 mm 以及110 mm 的七芯光纤,测量结果如表2 所示。

表2 七芯光纤芯间群延时差的弯曲依赖性测量结果Table 2 Measurement results of bending dependence of the inter-core DGD of 7-core fiber
比较表2 中三个不同弯曲半径的测量结果可发现,随着弯曲半径的增大,中间芯与外围芯的芯间群延时差不断减小,与理论分析一致。通过中间芯与外围芯的芯间群延时差的测量结果可计算出相邻外围芯之间的群延时差,随着弯曲半径的增大,外围芯的芯间群延时差也呈下降的趋势。
5 结论
本文提出了基于空间干涉成像的多芯光纤芯间群延时差测量方法,测量了七芯光纤芯间群延时差并研究了其芯间群延时差的弯曲依赖性。同时激发3 个芯时的测量结果分别与只激发这3 个芯中任意2 个相邻纤芯时的测量结果一一对应,验证了测量结果的准确性,且测量误差仅为1×10−4ps/m,说明该方法不仅可测量两芯间的群延时差,还可同时测量多个芯之间的群延时差。当改变七芯光纤的弯曲半径时,芯间群延时差的测量结果会随着弯曲半径的增大而呈下降的趋势,与理论分析一致。提出的空间干涉成像法测量简单快速、精度高,可广泛应用于SDM 系统和MWP 信号处理等应用场景中多芯光纤的芯间延时差测量研究。

