共引网络中样本量对相似性测度的选择影响

马振 贾保先

摘 要：选择合适的相似性测度推断共引网络，对于提升网络的关联性和真实性具有重要意义。然而，样本量的大小对相似性测度选择的影响尚未可知。基于样本量大小的敏感性，分别使用两个常用的相似性测度Phi相关系数（简称Phi）和Ochiai系数（简称Och）推断共引网络，通过网络节点属性和拓扑结构对推断的网络质量进行评价。结果显示：与Phi相比，Och推断的共引网络对样本量具有强鲁棒性。随着样本量的变化，Och推断的共引网络一直都遵循小世界特性，而Phi则不符合此特性。研究结论可以推广到其他遵循小世界特性的事务推断网络。同时，研究可以充实网络技术研究领域的基础理论。

关键词：相似性测度;样本量;共引網络;Ochiai系数;Phi相关系数

中图分类号：TP393.0 文献标志码：A

0 引言（Introduction）

共引网络的节点交互是通过两个文献节点之间的共引关系推理得出的[1]。共引关系中的两个节点可视为二元变量，计算共引关系实质就是计算两篇文献节点之间的共引关联性[2]。在共引网络中，由于网络结构和节点属性取决于节点间定义的连接索引，每一对节点之间的相似度是通过事务中的节点本身或共有邻节点的度数进行相似性计算得到的，因此选择合适的相似性测度是创建可靠、健壮的共引网络的必要条件[3]。相似性测度通常选择Phi相关系数（简称Phi）和Ochiai系数（简称Och）。Phi反映了两个变量之间的线性关系，对值为零的节点非常敏感，会导致节点之间的低重叠;而Och对值为零的节点具有强免疫性[4-6]。

尽管学者对Phi和Och已经有了充分研究与讨论[7-8]，然而前人的研究未考虑样本量的大小对相似性测度选择的影响。随着样本量的变化，节点本身及其相互间的关联性都会发生变化，连接的边也可能会受到事务数变化的影响。因此，有必要研究确定哪种相似性测度不受样本量变化的影响。针对上述问题，本文选择两种常用的相似性测度，针对样本量的敏感性，比较哪种相似性测度构建的网络具有强鲁棒性，这对于提升共引网络的质量具有重要意义。

1 相关概念（Relevant concepts）

1.1 计算公式

通过定义连接节点的边构成网络。共引网络是要创建一个无向加权网络，定义包含相关节点的事务，这些事务用于解释两个节点之间是否存在连接。由N 个事务发展而来的网络G 用G=（D，E）表示，其中D 是一组d 节点，E 是一组e 边，E⊆D×D。对称的d×d 矩阵AG =（aij）（ij ）∈D×D 称为G 的邻接矩阵。如果（i，j）∈E 是G 的边，则aij>0;如果（i，j）∉E，则aij=0;如果i=j，则aij=0。由于要比较Phi和Och推断的共引网络，因此基于这两个相似性测度定义了边aij。在Phi网络中，aij 表示PHIij，使用公式（1）计算得到：

由于很难找到Och的统计学定义，因此有学者利用相关系数检验显著性的方法确定Och的阈值，具体步骤如下[8]。

Step1：对于每对节点，计算总体数据集（最大样本量）的Ci、Cj、Cij、PHIij、t值和Ochij。

Step2：求节点对数q，t>2.58（即连接在α=0.01时显著相关）和Cij > ΣCij/p，其中p 是Cij >0的对数。

Step3：在给定的Cij > ΣCij/p 中，求出对数等于q 的Och阈值Sc。

Step4：使用Sc 作为阈值，在不同的样本量中查找边的数量。

由 于Step3中计算Sc 的对数等于Phi的最大对数，因此该方法使用Phi和Och从最大样本量中推断的网络边数相同。

1.2 节点属性和拓扑结构

评价不同相似性测度推断的网络质量可以从局部属性和全局属性两个方面考虑，局部属性主要根据的节点度量指标衡量每个节点，全局属性根据拓扑结构从整体上评价网络质量[9]。网络节点的度量指标主要包括度中心性、加权度、中介中心性等。表1中列出了节点的度量指标定义。

聚类系数反映了网络的连接紧密程度，是衡量网络拓扑结构普遍且重要的指标[12-14]。复杂网络的拓扑结构有很多种，通常比较常见的有随机网络、无标度网络和小世界网络，拓扑结构通常有随机、无标度和小世界。如果一组节点之间的连接是以一定的概率随机连接的，则称为随机网络，随机网络中节点的度中心性服从二项分布。当网络中少数节点起主导作用时，称为无标度网络，无标度网络中节点的度服从幂律分布。当网络中有多个节点簇使得节点之间的距离变小时，称之为小世界网络，小世界网络的度可以服从任意分布，其聚类性能高于随机网络和无标度网络。通常使用特征路径长度和聚类系数衡量小世界网络。

2 数据采样（Data sampling）

选取Web of Sicence数据库中截至2022年12月31日的数据源。为了尽可能地确保研究结果的准确性，同时考虑到工作量，选择Scientometrics 期刊，下载10个数量不同的论文题录数据为样本，涵盖了从小到大10个不同数量的数据样本。评估数据的质量，清理数据（去除社论、校正、会议论文、书评、信函、提前发表论文等），然后分别使用Phi和Och推断出20个共引网络。

样本包括（1）2008年发表的128篇论文;（2）2013年发表的255篇论文;（3）2020年发表的439篇论文;（4）2021—2022年发表的746篇论文;（5）2020—2022年发表的1 185篇论文;（6）2019—2022年发表的1 485篇论文;（7）2018—2022年发表的1 858篇论文;（8）2017—2022年发表的2 230篇论文;（9）2013—2022年发表的3 520篇论文;（10）2008—2022年发表的4 535篇论文。

创建20个共引网络，其中使用p<0.01的Phi推断了10个共引网络，使用阈值为0.04的Och推断了10个共引网络。例如，使用样本（8），Phi推断的共引网络有1 957条边显著相关，Och推断的共引网络有3 894条边显著相关。

3 实证分析（Empirical analysis）

3.1 不同样本量对网络节点的影响

如图1所示，随着样本量的增加，Phi推断的网络中相关边数显著增加。例如，样本量为1 485时，Phi推断的网络包含1 265条边;样本量为746时，Phi推断的网络包含562条边;样本量减半时，Phi推断的网络边数也接近减半。在Och推断的网络中，样本量大于1 185时，Och推断的网络边数变化比较缓慢;样本量小于1 185时，Och推断的网络边数变化较明显。

网络密度如图2所示，Och推断的网络密度在所有样本中基本保持不变;相反，在Phi推断的网络密度发生了较大的变化。这说明样本量的变化对Och创建的共引网络的网络密度影响较小。

从图3—图8中可以观察到，样本量大小对共引网络的其他网络度量指标的影响。在Phi推断的网络中，平均度中心性、平均加权度中心性、平均中介中心性、平均紧密中心性、平均聚类系数及平均特征向量中心性都随着样本量的增加而增加。在Och推断的网络中，平均度中心性、平均加权度中心性、平均紧密中心性、平均聚类系数及平均特征向量中心性基本保持不变，直到样本量减少到128时，指标才有所波动;此外，Och推断的网络的平均中介中心性是所有网络度量中最不一致的，在样本量减少到1 185时，平均中介中心性发生了明显的变化。可见，在样本量较小的情况下，平均中介中心性并不是一个有效的度量指标。

3.2 不同样本量对网络拓扑结构的影响

当网络中特征路径长度很短且存在多个节点簇时，网络具有小世界特性。特征路径长度和聚类系数是小世界网络的度量指标。节点i 和节点j 之间的距离dij 定义为连接这两个节点的最短路径上边的数目。网络的特征路径长度P 就是任意两个节点之间距离的平均值，计算公式如下：

对于具有小世界特性的网络，需要满足条件n ≫k ≫ln n≫1，确保网络不会分割成多个子网络。此外，必须满足两个条件：首先，网络的特征路径长度（共引网络的特征路径长度用Pcom 表示）与相同节点数n 和平均度k 的特征路径长度（随机网络特征路径长度用Prand 表示）大致相同;其次，网络的聚类系数（共引网络聚类系数用Ccom 表示）应大于等价随机网络的聚类系数（等价随机网络聚类系数用Crand 表示）。

为了判断网络的小世界特性，本文将研究重点放在每个网络的最大连通部分上，连通部分包含直接或间接连接的最大连接节点数。例如，样本（8）创建的Phi网络的最大连接组件包含473个节点，该最大连接组件的平均度为25，即n=473和k=25，Prand 和Crand 可分别通过公式（6）和公式（7）计算得到：Prand～1.91，Crand～0.053，Pcom 为2.452（大于Prand），Ccom 为0.641 4（大于Crand）。此外，满足n≫k≫ln n≫1（473≫25≫6.16≫1）。因此，遵循小世界特性。

Prand～ln n/ln k （6）

Crand～k/n （7）

如图9所示，随着样本量的增加，Phi推断的网络中最大连接集的节点数也随之增加。然而，Och推断的网络中最大连接集的节点数量基本没有变化，直到样本量减少到255时才急剧减少。

关于网络特征路径长度的变化，如图10和图11所示，随着样本量的减小，Och推断的网络中的Prand 和Pcom 几乎保持不变，但是Phi推断的网络显示出一些不一致性。在Phi推断的网络中，Prand 随着样本量的增加逐渐增加，Pcom 在样本量增加到439之前先增加，之后随着样本量的增加而减少。

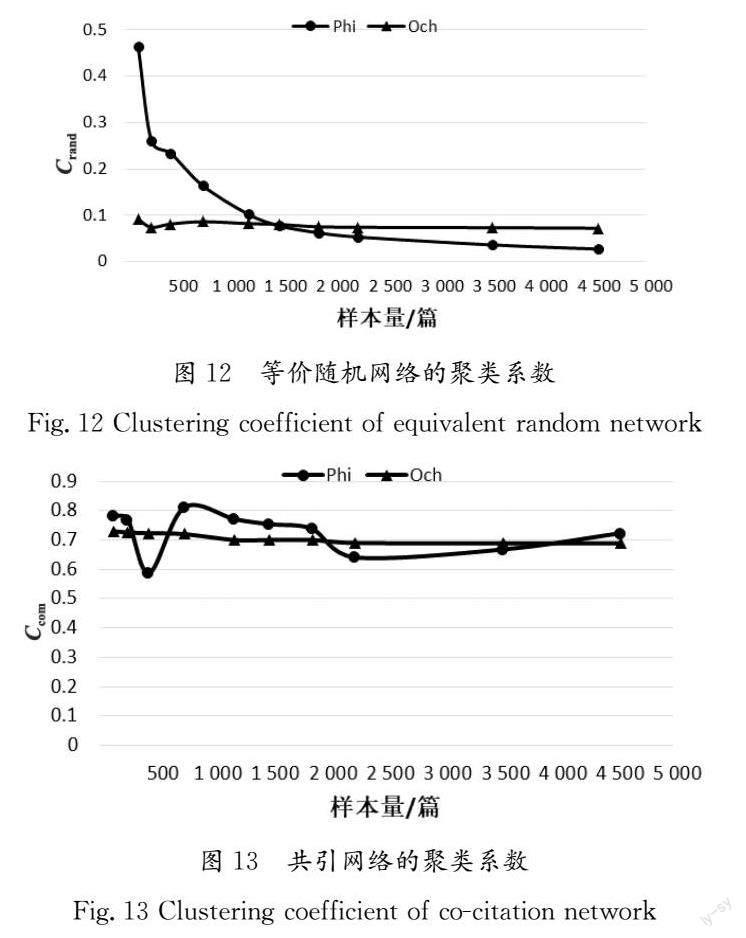
在图12和图13中可以看到，聚类系数的变化也有类似趋势：在Och推断的网络中，Crand 和Ccom 基本保持不变，而在Phi推断的网络中，Crand 随样本量的增加逐渐减少且变化差异较大，Ccom 随样本量的变化有轻微的随机变化。

在Phi推断的网络中，样本量为4 535时，满足小世界特性。但是，随着样本量的减少，k 和ln n 之间的差异变小，这违反了小世界特性的条件要求，形成多个不连通的子网络。此外，在Och推断的网络中，小世界特性始终存在。总体而言，Och保留了网络的整体拓扑结构，样本量较小时也遵循小世界特性，而Phi则不符合这一特性。

4 结论（Conclusion）

本文分析了共引网络中样本量对相似性测度选择的影响，分别使用两个常用的相似性测度Phi相关系数和Ochiai系数推断共引网络，通过网络节点属性和拓扑结构对推断的网络质量进行评价。结果表明：如果目标是寻找高度相关的节点，可以使用Phi;在样本量较小的情况下，建议使用Och。本文研究可以丰富网络技术研究领域的基础理论，提升推断关系网络的关联性和真实性。此外，研究结论可以推广到神经网络、语言网络、文本网络等其他遵循小世界特性的通过事务推断得出的网络。

参考文献（References）

[1] 邱均平. 文献计量学[M]. 北京：科学出版社，2019：252-255.

[2] GUILFORD J P. Psychometric methods[M]. New York：McGraw-Hill Book Company，1936：13-22.

[3] 楊利军，张良友. 期刊共被引相似性测度问题的实证研究[J].图书情报工作，2010，54（18）：139-144.

[4] 曾守桢，骆丹丹. 基于类Pearson综合相关系数的概率语言TOPSIS多属性决策方法[J]. 系统科学与数学，2021，41（1）：126-143.

[5] 高继平，丁堃，刘宇，等. 知识基础与前沿载文间的知识流动分析：以信息领域中的Gerard Salton为例[J]. 情报杂志，2009，28（10）：98-102.

[6] 康耀红，CHANG K W. 关于Salton扩展布尔情报检索模型的一个注记[J]. 情报学报，2002（2）：164-166.

[7] CHARTIER J F，MONGEAU P，SAINT-CHARLES J.Predicting semantic preferences in a socio-semantic systemwith collaborative filtering：a case study[J]. InternationalJournal of Information Management，2020，51：102020.

[8] EGGHE L，LEYDESDORFF L. The relation between Pearson'scorrelation coefficient r and Salton's cosine measure[J].Journal of the American Society for Information Scienceand Technology，2009，60（5）：1027-1036.

[9] 孙睿，罗万伯. 网络舆论中节点重要性评估方法综述[J].计算机应用研究，2012，29（10）：3606-3608，3628.

[10] 胡思文，李兵，何鹏，等. 一种基于h指数的软件网络中重要类的度量方法[J]. 小型微型计算机系统，2017，38（2）：249-253.

[11] 刘向. 知识网络的形成与演化[M]. 武汉：武汉大学出版社，2014：32-33.

[12] HERNÁNDEZ SERRANO D，SÁNCHEZ GÓMEZ D.Centrality measures in simplicial complexes：applicationsof topological data analysis to network science[J]. AppliedMathematics and Computation，2020，382：125331.

[13] 马梦珂，倪静. 基于度值和聚类系数的跨单元调度问题优化[J]. 计算机应用研究，2021，38（9）：2651-2656.

[14] 杨博，刘大有，金弟，等. 复杂网络聚类方法[J]. 软件学报，2009，20（1）：54-66.

作者简介：

马 振（1984-），男，硕士，讲师。研究领域：知識网络，数据挖掘。

贾保先（1982-），男，博士，副教授。研究领域：人工智能，大数据。