德西特时空中RN黑洞的相变动力学

郭雄英，杜云芝，李怀繁

（山西大同大学物理与电子科学学院，山西大同 037009）

1983 年，Hawking 和Page 提出AdS 时空的Hawking-Page(HP)相变可以给出不同阶段的时空演化[1]。也就是说，随着温度的升高，处于支配地位的位形从纯热辐射相，变到AdS 黑洞和热辐射的共存相，最后到稳定黑洞。在文献[2]中，Witten 将其解释为限制/解除限制阶段中规范理论的转变。也可以将宇宙学常数视为压强，共轭变量视为热力学体积，把该相变理解为固/液相变[3]。随后，扩展的AdS/dS 相空间中的相变被广泛研究[4-20]。

众所周知，普通热力学系统的相变是物质微观组分之间竞争的结果。由于黑洞具有与普通热力学系统相似的热行为，黑洞的微观结构成为热门话题。文献[21]利用Ruppeiner 几何的Ruppeiner 标量曲率研究了AdS 黑洞微观结构[22]。引入推测黑洞分子数密度来检查其相变和微观结构。通过不同的Ruppeiner 标量曲率值来表示黑洞分子间不同类型的相互作用，这种方法很快被推广到对其他黑洞的研究中[23-28]。

与平衡热力学相比，研究相变的动力学过程是一个具有挑战性的问题。受吉布斯自由能研究蛋白质折叠的启发[29-30]，蛋白质折叠过程可看作是随机Fokker-Planck 方程描述的状态的相变[31]。最近，Li 和Wang 提出了一种基于吉布斯自由能图谱的黑洞相变动力学过程的启发式处理方法[32-33]。描述随机物理变量分布的Fokker-Planck 方程的随机处理已广泛应用于化学、生物学、物理学和天体物理学[34-38]。从自由能景观的角度来看，黑洞事件视界是序参数，黑洞相变被视为序参数的随机热波动[39]。序参数概率分布的演化由Fokker-Planck 方程控制。

Hawking-Page 相变的运动学过程在广义相对论和有质量引力理论中进行了研究。发现黑洞有一定的概率从黑洞变到热AdS 空间，反之亦然[32,40]。这种方法被推广到带电AdS 黑洞相变动力学过程的研究，其中考虑了亚稳态黑洞和稳态黑洞之间的转换过程[33]。通过对Fokker-Planck 方程进行数值计算，结果表明初始的小黑洞倾向于变换到大黑洞，并且也可以发生相反的过程。对五维中性Gauss-Bonnet AdS 黑洞的自由能景观相变动力学过程的研究表明，物理黑洞对应于离壳吉布斯自由能的极值点，稳定的小/大黑洞相变的势垒高度随温度的升高而降低[41]。此外，对六维带电Gauss-Bonnet AdS 黑洞自由能景观相变动力学特性的研究表明，三相点表现出有趣的振荡行为[42-43]，以及精暗能量对黑洞相变动力学影响的研究表明，精暗能量的状态参数越大，黑洞系统演化得越快[44]。对吉布斯自由能的研究表明它可能揭示黑洞潜在的微观相互作用[39,45]。

另一方面，德西特空间中的强引力理论与共形场论之间存在对应关系[46]。具有黑洞的dS 时空的热力学研究很有趣，也很重要[47]。这是因为早期暴胀阶段的宇宙是一个dS 时空，在遥远的未来它将再次变成dS 时空[48-49]。此外，类似AdS 时空中存在AdS/CFT 对应，dS/CFT 对应可用于dS 时空[50]，其中探讨了有关各个维度可能相变的更多信息。在上述工作的努力下，dS/AdS 时空中黑洞已被广泛认为是热力学系统。更重要的是，黑洞的观测为其热力学研究打开了新的窗口。

dS时空中的黑洞，由于存在具有不同温度的多个视界，一般不能处于热力学平衡状态。由于系统存在引力，需要考虑黑洞视界与宇宙视界的相互作用，即对于黑洞外部视界（一般称为黑洞视界）与宇宙视界之间的空间，两个视界上不同的霍金辐射温度使得dS黑洞不能像普通的热力学系统一样处于平衡状态。由于黑洞视界和宇宙视界具有共同的参数M、Q，因此，两个视界上的热力学量不是独立的。在构造处于热力学平衡状态的dS黑洞的等效热力学量时，必须考虑两个视界之间的相互作用。基于此，研究了四维RN-dS时空中相变的动力学特性，分析了四维RN-dS黑洞的吉布斯自由能景观行为，并探讨大体积/小体积相变的动力学过程，采用自然单位制G=c=k=ℏ=1。

1 四维RN-dS黑洞的相变

四维时空中的RN黑洞解为

式中：M和q是黑洞的质量和电荷。

下面主要讨论Λ >0，k=1 的解，即RN-dS 黑洞解。该系统具有两个视界，一个是黑洞视界r+，另一个是宇宙视界rc。这两个视界均满足方程f(r+,c)=0。两视界的霍金辐射温度由文献[51]给出。将四维RN-dS 时空看成一个处于热力学平衡的普通热力学系统，考虑两个视界的相关性，可计算出有效热力学量(Teff,Peff,V,S,Φeff)。在此需要指出熵不仅是两个视界熵的总和，还包含两个视界之间的相关联项。考虑到黑洞视界与宇宙视界的联系，相应的黑洞热力学第一定律为

两视界之间的热力学体积和熵分别为

注意总熵不仅是黑洞视界熵和宇宙视界熵之和，F(x)中的(x)表示来自两视界关联的额外贡献。

等效温度、等效压强和质量如下：

对于等温、等压过程，黑洞视界半径满足以下关系

一阶相变点可通过麦克斯韦等面积定律得到。图1 中给出Peff-V和Teff-S一阶相变的相图。实际上一阶相变点是RN-dS 黑洞两个不同体积相的共存态。所有这些点构成一条共存曲线。表1 中给出不同条件下两相的热力学量数值。

表1 Teff ≤时两共存相的热力学量

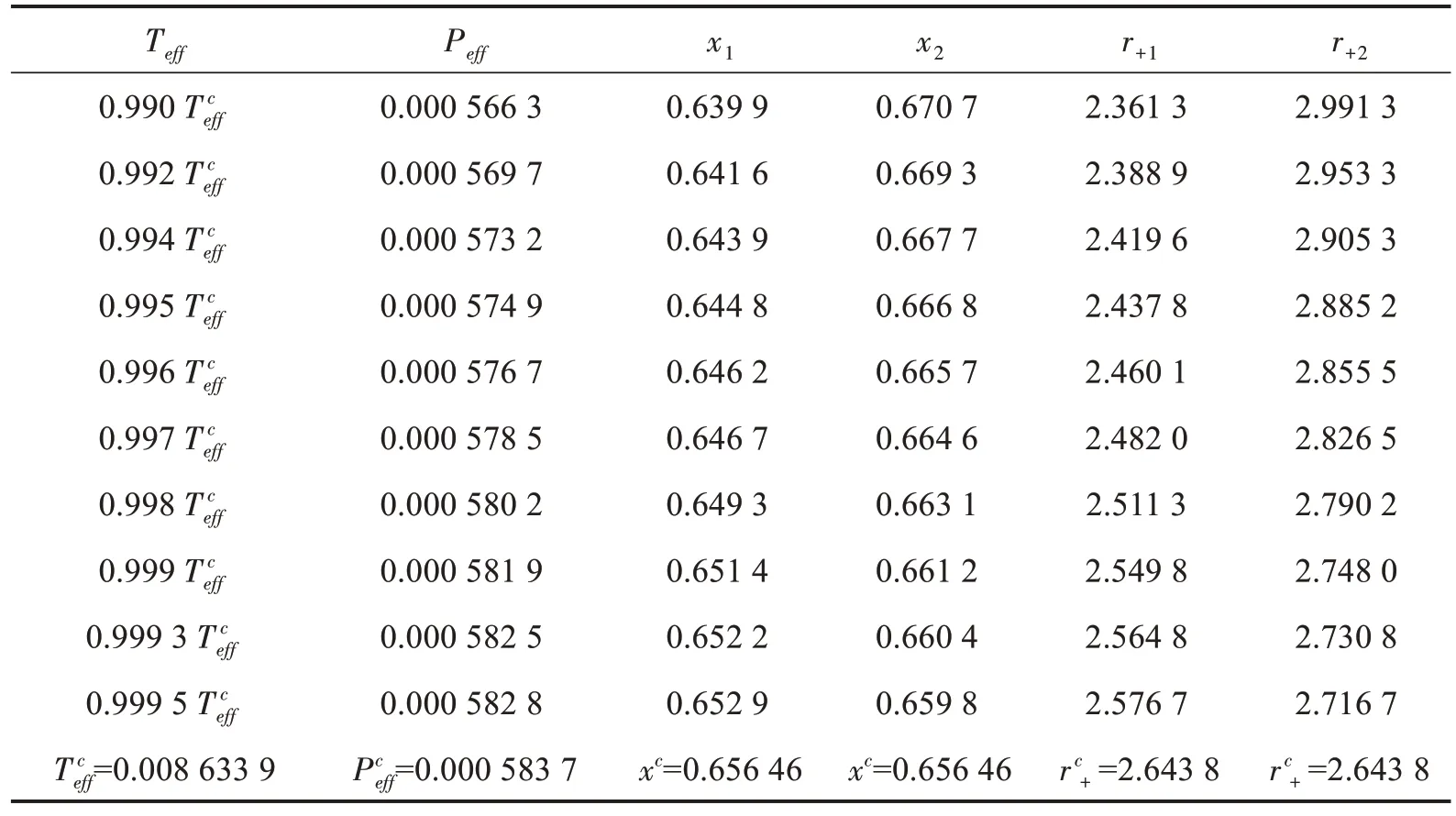
表1 Teff ≤时两共存相的热力学量

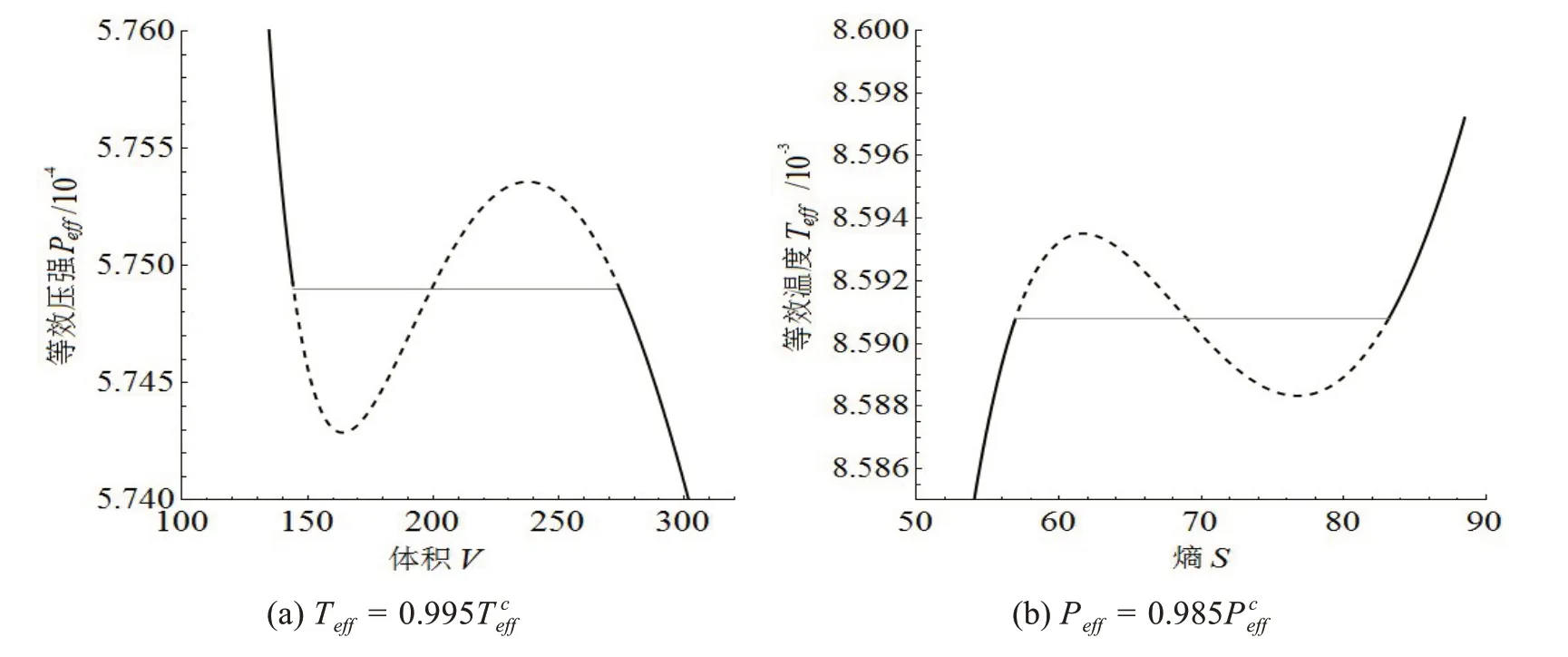
图1 Teff -S和Peff -V相图中的等面积定律

2 热力学相变的动力学性质

与等面积定律一样，吉布斯自由能可看作黑洞视界（或宇宙学视界）的函数，是研究相变的重要热力学量，它在一级相变点表现出燕尾行为。虽然它是连续的但在二阶相变时并不平滑。这两种方法在热力学上是等效的。最近，文献[32]中提出吉布斯自由能也应该对应于黑洞相变的动力学过程。下面从吉布斯自由能的角度研究四维RN-dS 时空的相变动力学。

2.1 吉布斯自由能

对于四维RN-dS 时空，文献[51]中提出存在大/小体积相变。下面将介绍参数q=1 时在相变点处发生的热动力学相变。

系统的吉布斯自由能景观定义为

其中T是相变温度，等于T0。在相变点处吉布斯自由能的行为如图2。从图中可见在相变点处，吉布斯自由能景观呈现出双阱行为，即存在两个局域极小值(图（a）位于rs=2.419 6，rl=2.905 3，图（b）位于rs=2.437 8，rl=2.885 2)，它们具有正热容量，相应于稳定的小/大体积态。位于rm处的局部极大值代表具有负热容的不稳定中间体积状态，并且充当稳定的小体积和大体积状态之间的屏障。在同一温度下，两个局部极小值的深度相同。此外，温度越高阱深越小。从吉布斯自由能的角度表明，在两个阱深度相同的情况下，会发生小体积/大体积相变。在这个问题上，预计重入相变或三相点可能对应于更多的吉布斯自由能阱。

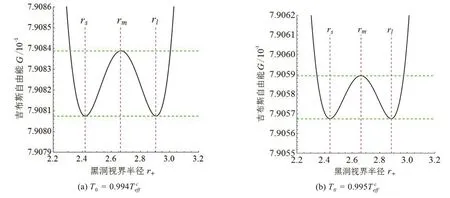
图2 相变点处G - r+图

2.2 Fokker-Planck方程和几率演化

当吉布斯自由能G的双阱具有相同深度时，会出现RN-dS时空的大体积/小体积相变。接下来将研究这个系统的动力学过程。

文献[32]提出黑洞相变的随机动力学过程可以通过吉布斯自由能的相关概率Fokker-Planch 方程来研究，这是一个控制宏观变量涨落分布函数的运动方程。对于黑洞热力学系统，视界r+是序参数，可以看作是相变过程中的随机涨落变量。基于此，将展示该系统在热涨落下的正则系综中的相变动力学过程。需注意正则系综由一系列具有任意视界的黑洞组成。这些黑洞状态的概率分布ρ(t,r+)满足关于吉布斯自由能的Fokker-Planck方程

其中：β=1/kT,D=kT/ξ是扩散系数，k是玻尔兹曼常数，ξ是耗散系数。为了不失一般性，令k=ξ=1。为了求解上述方程，应施加两种类型的边界(r+=r0)条件：一个是反射边界条件，它保持概率分布的归一化；另一个是吸收边界条件。

在这个系统中，左边界的位置应该小于rs，右边界的位置应该大于rl。这里可以将rmin=1 作为左边界rlb，将右边界rrb设为4.5。反射边界条件意味着概率流在左右边界处消失

吸收意味着几率分布函数在边界处消失ρ(t,r0)=0。边界条件的选取取决于所考虑的物理问题。

初始条件选为中心在ri的高斯波包

这里a是一个常数，决定了高斯波包的初始宽度，不影响最终结果。由于考虑小体积/大体积状态之间的热动态相变，ri可以设置为rs或rl。这意味着该热系统最初处于小体积或大体积状态。

概率分布的时间演化如图3，其中T0==0.000 574 9，a=0.1。当t=0 时，高斯波包位于大体积相（图3（a））和小体积相（图3（b）），它们都随着时间t的增加而减小，直到趋于某个常数。然而，与此同时图3（a）r+=rs处和图3（b）r+=rl处的ρ(t,r+)的值从零增加到相同的常数。这表明大体积相中dS 时空趋向于小体积相，如图3(a)，而小体积相的dS 时空则趋于大体积相，如图3(b)。最终系统在短时间内达到大体积/小体积共存的稳定状态。为了使大/小体积相变的动力学过程更加清晰，在图4 中展示了在相变点处ρ(t,rl) 和ρ(t,rs)的概率分布。初始大体积相（或小体积相）概率分布最大，而相应的小体积相（或大体积相）态为零。随着时间的增加，它们都趋近于相同的值。这与G-r+中显示的一致，即大体积和小体积状态在吉布斯自由能景观的双阱中具有相同的深度。

图3 不同初始条件下相变点处ρ(t,r+)图

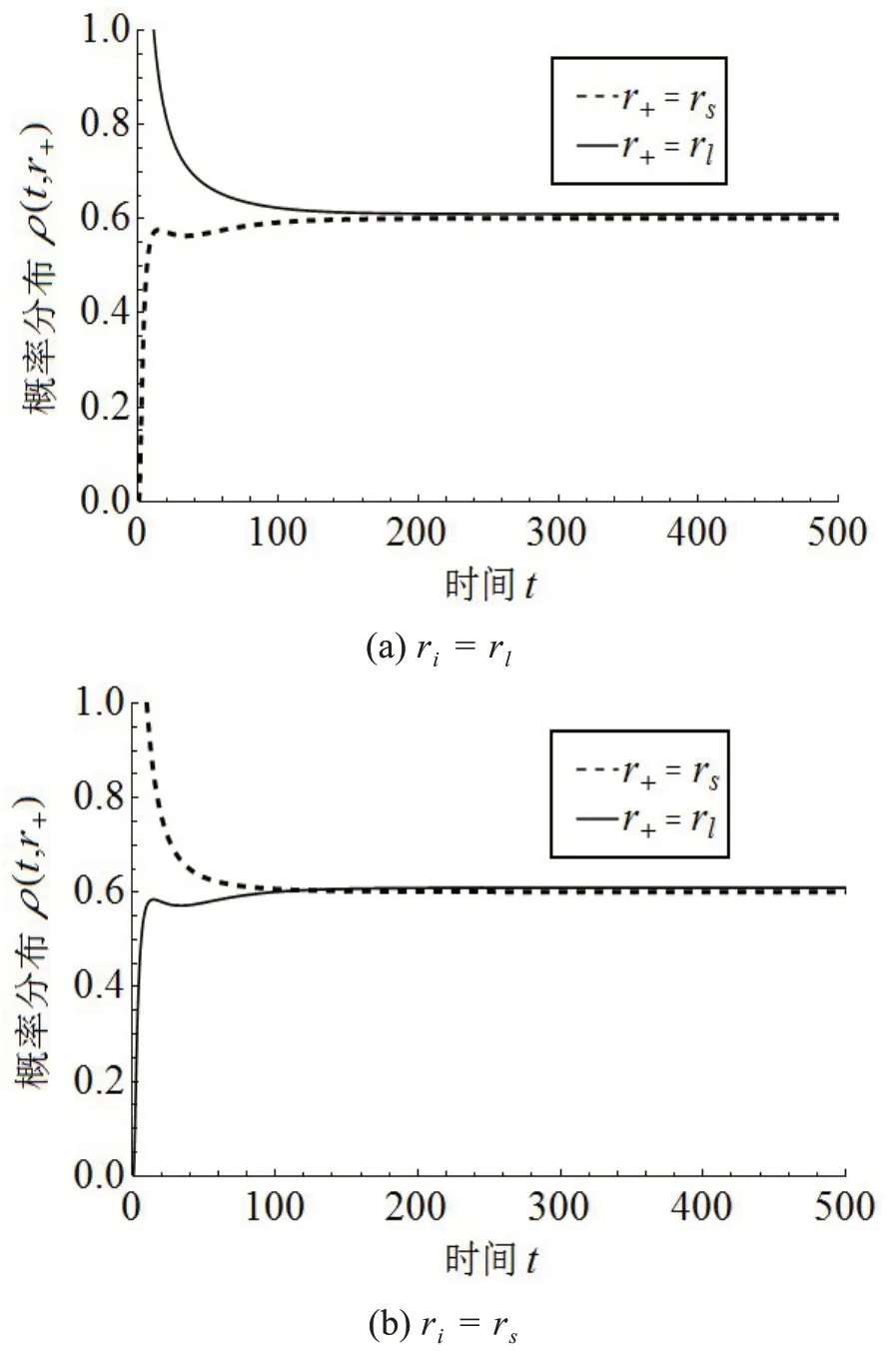
图4 不同初始条件下相变点处ρ(t)图

2.3 首次通过时间

一般来说，大体积/小体积相变动力学过程中的重要量用首次通过时间来表征，其定义为稳定的大体积相或小体积相逃逸到不稳定的中间体积状态（即，从一个阱到吉布斯自由能的势垒）的首次通过时间的平均值。

假设在稳定的大体积相或小体积相中存在一个理想吸收体，如果系统在热涨落下进行了第一次通过，系统将离开这个状态。将∑定义为第一次通过时间内动力过程的总概率，有

其中：rm，rmin，rrb分别为RN-dS 黑洞视界的中间、极小和右边界。当经过的时间足够长时，稳定HPBH或者LPBH 态的几率变为零，即或如上所述，首次通过时间是一个随机变量，因为相变的动力学过程是由热涨落引起的。因此首次通过时间可表示为

显然Fpdt表示系统在时间间隔(t,t+dt)内通过黑洞中间态的几率。考虑方程（10）和（13），首次通过时间的分布变成

此处Fokker-Planck 方程的吸收和反射边界条件位于rm以及另一端(rmin或rrb)。注意几率分布无需归一化处理。

通过求解具有不同相变温度（T0=和T0=的Fokker-Planck 方程（10）并将它们代入方程（13）和（15），得到初始条件ri=rl的数值结果，如图5。由于采用初始条件ri=rs的结果与采用初始条件ri=rl的结果相同，这里只展示一种情况。很明显，对于两个不同初始条件的AdS 黑洞，Fp的行为是相似的。在具有固定温度的Fp曲线中，在t=0 附近出现一个单峰。这可以理解为在很短的时间间隔内发生了大量的首次通过事件，概率分布随时间呈指数衰减。相变点处的温度对Fp的影响与吉布斯自由能的影响一致。这意味着温度越高，概率下降越快，相变越容易发生，势垒深度越小；否则温度越低，概率下降越慢，相变越难发生，势垒深度越高。

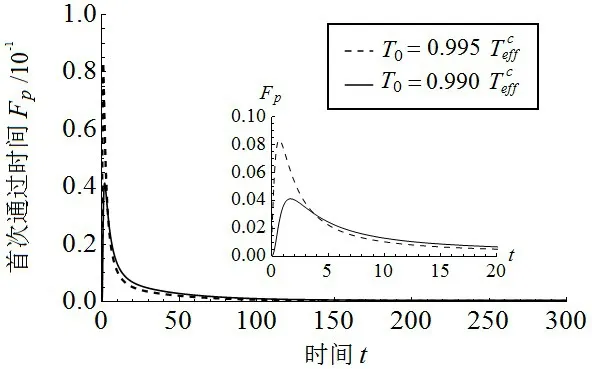
图5 不同温度下的Fp - t关系图

3 讨论和结论

由于黑洞对应的热力学状态的精确统计描述尚不明确，研究黑洞的dS 时空热力学相变成为人们关注的问题。从吉布斯自由能的角度研究了四维RNdS 时空的大/小体积相变的动力学特性。

首先回顾了RN-dS 时空的热力学性质，提出相变是大/小体积相变。当时，可以根据麦克斯韦等积定律构建T-S图中的HPBH/LPBH 相变。由于利用麦克斯韦等面积定律和吉布斯自由能，得到的结果都是相同的，因此文中未介绍吉布斯自由能的燕尾行为。

吉布斯自由能G中存在双阱。G的两个局部最小值对应于稳定的大/小体积状态。局部最大值代表不稳定的中间体积状态，并充当稳定的大体积和小体积状态之间的屏障。此外，两个阱的深度相同。这表明从G的角度来看，当两个阱具有相同的深度时，将发生大/小体积相变。然后研究了由Forkker-Planck 控制的大/小体积相变的动力学过程方程。通过在最小黑洞视界和仅大于大体积状态的值上施加反射边界条件，并以小体积或大体积状态的高斯波包作为初始条件，得到了Forkker-Planck 方程的数值结果：小体积或大体积状态的初始高斯波包随时间的增加而减小，但同时小体积或大体积状态的ρ(t,r+)的另一个峰值状态从零增加到相同的常数。这表明随着时间的增加系统将从初始状态离开到另一个状态，直到它变成一个双态共存状态，这一结果是与在吉布斯自由能G中在两个阱的深度（代表小体积和大体积状态）的值相等是一致的。

最后考虑了首次通过时间。通过对中间势黑洞态施加吸收边界条件，并以小体积或大体积态的高斯波包作为初始条件，也得到了Forkker-Planck 方程的数值结果：无论考虑何种初始条件，Fp的行为对于两个不同的初始条件都是相似的。Fp在t=0附近存在一个单峰。这可以理解为在很短的时间间隔内发生了大量的首次通过事件，概率分布随时间呈指数衰减。从相变点温度对Fp和G的影响可知，温度越高，概率下降越快，相变越容易发生，势垒深度越小；否则温度越低，概率下降越慢，相变越难发生，势垒深度越高。