基于正交贴体网格的黏弹介质地震波模拟

刘志强，黄磊，李钢柱，牛兴国，张晓萌

（1.内蒙古农业大学水利与土木建筑工程学院，内蒙古呼和浩特 010018；2.内蒙古有色地质矿业（集团）物探勘查公司，内蒙古呼和浩特 010010）

0 引言

受到地层黏滞性的影响，地震波在地下介质中传播时能量会衰减，这种衰减在地表附近尤为严重。若用完全弹性模型模拟地下真实介质，结果与实际差别较大。研究表明，黏弹模型可以较精确地反映地层的吸收作用，近似代替实际地下介质更为合理。很多学者对黏弹介质中的地震波场进行了数值模拟。Robertsson等［1］设计了二维速度—应力交错网格模拟方法，并推广至三维黏弹模型［2］；Xu等［3-4］实现了三维起伏地表黏弹模型的数值模拟，并通过定义新的复合记忆变量有效节省了计算机内存；Štekl等［5］在频率域用旋转有限差分算子对黏弹模型进行了精确的数值模拟。在中国，宋常瑜等［6］利用有限差分法进行了井间数值黏弹模拟，并分析了地震波在井间的传播特征；唐启军等［7］利用有限差分法模拟了黏弹单斜各向异性介质中的地震波场；陈玉玺等［8］研究了三维黏弹介质地震波场数值模拟技术；陈豪等［9］利用交错网格有限差分法模拟了三维黏弹性介质中的地震波场，并分析了品质因子对波场特征的影响。

常用的数值模拟方法包括有限差分法［10-12］、伪谱法［13-14］、有限元法［15-16］、普元法［17-18］等。其中有限差分法因具有原理简单、易编程实现、计算效率高、对内存需求相对较小等特点，在地震波数值模拟中使用最广泛。常规有限差分法采用笛卡尔坐标系下的规则网格，在模拟起伏地表时必然会出现阶梯状的边界，从而引起虚假散射波。为减弱这种虚假散射波，需采用精细网格，这会导致存储量的增加和计算量的增大。因此，发展了可变网格和不规则网格地震波数值模拟方法。Hayashi等［19］采用空间变网格法加密起伏地表附近的网格，从而尽量消除阶梯状网格带来的误差，同时能减小计算量。董良国［20］和Tarrass 等［21］利用纵向坐标变换思路，将起伏边界变换为水平边界，然后在变换后的矩形网格中采用有限差分法求解地震波方程。但是他们的方法只适用于地形起伏较缓的情况，在起伏较大时容易出现不稳定现象。Lan 等［22］、Sun等［23］在贴体网格下使用同位网格有限差分法求解波动方程，能够适应任意起伏地表，计算精度较高，但为了满足自由边界条件需要做繁杂的坐标旋转和插值运算。为此，蒋丽丽［24］、丘磊［25］、李庆洋等［26］提出采用正交贴体网格对起伏地表模型进行网格剖分。

在对现有各种起伏地表地震波数值模拟方法进行研究的基础上，本文将Zhang 等［27］提出的改进RL（Ryskin & Leal）正交贴体网格生成技术［28］引入起伏地表下黏弹介质的网格剖分，采用牵引力镜像法实现起伏地表处的自由边界条件。由于采用了正交贴体网格，可以直接实施笛卡尔坐标系下的自由边界条件，从而避免了繁杂的坐标旋转或插值运算。在曲线坐标系中，通常情况下变量并非严格定义在半网格点上［29］，因而必须进行复杂的插值运算求取没有定义在交错位置上的变量值，这不仅会降低计算效率，还极大地影响了差分算法的精度。因此，本文采用Boegy等［30］提出的选择性滤波同位网格有限差分法计算曲线坐标系下的一阶速度—应力方程。最后通过数值算例验证本文方法的精度和适用性。

1 网格剖分方法

正交贴体网格生成实际上是一个数学变换过程，即由任意形状的物理域(x，z)变换到直角四边形的计算域(ξ，η)（图1）。在这个变换中点与点之间存在一一对应关系，在数学上可以表示为

图1 网格映射示意图

RL 正交贴体网格可由（x，z）平面上的一对Laplace方程生成［28］

式中：x，ξ≡∂x/∂ξ表示x对ξ的一阶导数；f是畸变函数，由ξ和η方向的刻度因子给出，具体形式为

式中：hξ和hη分别表示ξ和η方向的正交刻度因子；gξξ和gηη是包含坐标系信息的度量张量分量，计算公式为

如果f= 1，式（2）就变成保角变换，则f= 1称为完全光滑条件。对于地表起伏不大的模型，通过式（2）基本可以确保内部网格具有较优秀的正交性和光滑性。但是，当地表起伏比较大时，为了保证边界上的正交性，往往会造成内部网格点的严重畸变（图2）。为此，Zhang等［27］引入ξ、η方向的光滑刻度因子(ξ)i和(η)j，并通过与正交刻度因子加权平均得到改进的畸变函数

图2 内部网格点严重畸变的网格剖分示意图

式中：i和j分别为ξ和η方向的网格点序号；Nξ和Nη是ξ和η方向的网格点总数；rξ和rη是经验参数，可以取常数，也可以根据以下公式计算

利用改进的RL 算法兼顾了网格剖分的正交性和光滑性，避免了起伏地表附近网格点的畸变（图3）。

图3 改进后的RL 正交贴体网格剖分示意图

2 数值模拟方法

2.1 曲线坐标系下的黏弹介质波动方程

利用链式法则和笛卡尔坐标系下的Kelvin 黏弹介质一阶速度—应力方程，可以推导出曲线坐标系下的二维黏弹介质一阶速度—应力波动方程。矩阵形式的波动方程可表示为

式中：U为由速度和应力组成的列矩阵；为U对时间的一阶微分；A、B、C、D是系数矩阵。具体有

其中：vx、vz分别表示速度的水平分量和垂直分量；τxx、τzz、τxz为应力分量；ρ为密度；λ、μ、λ'和μ'为拉梅系数，与纵、横波速度vP、vS及纵、横波品质因子QP、QS的关系为

式中ω为圆频率。

2.2 空间离散算法

对式（11）的空间导数，本文用优化的7 点同位网格中心差分格式［31］求解。该格式中所有变量和模型介质参数都定义在同一个网格点上（图4）。对于一维问题的差分格式为

图4 优化的7 点同位网格有限差分示意图

式中：Δξ为空间步长；aj为中心差分系数。

中心差分格式只能用于内部网格点上变量偏导数的离散求解，对于模型边界附近的网格点，由于缺少模型外网格点上的变量值，因此必须使用非中心差分格式求解。本文釆用Berland 等［32］提出的7 点非中心差分格式计算边界网格点上的偏导数

式中：P=1或2，Q=5或4；bj为非中心差分系数。

同位网格差分格式在求解一阶速度—应力波动方程时会产生高频的格点振荡现象。为了消除格点振荡带来的影响，对式（18）和式（19）的计算结果做选择性滤波处理

式中：ud为经过滤波后的波场；F为滤波衰减函数；σ∈[0，1]是滤波衰减因子；dj为滤波算法的权系数。当P=Q=3时，对中心差分格式计算结果进行滤波；P=2、Q=4 和P=1、Q=5 时，对非中心差分格式计算结果进行滤波。

2.3 边界条件的实施

图5 是自由界面附近垂直方向导数的离散求解示意图。设j=n为自由界面。图中点A、B为内部网格点，采用7 点中心差分格式求解。点C、D为边界网格点，分别采用非中心差分格式求解。在正交贴体网格下，由于地表处网格线上的法向量与地表正交，因此可以直接采用水平界面时的自由边界条件。根据自由边界条件，地表网格点上的两个应力分量为零，即

图5 自由边界处有限差分格式示意图

自由地表以上虚拟网格点上的应力则可以根据应力镜像法求得，即

在自由地表处对式（11）中的应力水平分量进行求解时，需要用到速度分量在η方向上的导数。将式（21）代入式（11）并整理，可得速度自由边界条件

利用式（23）可求出vx在η方向的导数，vz在η方向的导数可以用相同的方法求取。因此，利用式（21）～式（23）就可以完整的实施自由边界条件。

其他边界采用基于辅助微分方程的完美匹配层（ADE-PML）吸收边界条件［33］消除人工边界反射。

3 数值算例分析

3.1 起伏地表均匀介质模型

为了测试本文方法对起伏地表模型的有效性和精度，设计如图6a 所示的起伏地表均匀介质模型，参数为：vP=3.3 km/s，vS=2.2 km/s，ρ=2.0 g/cm3，QP=25，QS=20。图6b 为利用本文方法得到的正交贴体网格，其计算域中两个方向的空间网格步长都为5 m。可以看出，本文提出的网格剖分法不仅能够精确描述起伏地表，而且在边界上具有精确的正交性。主频为75 Hz的Ricker子波作为震源，位于（500 m，5 m）处，分别采用本文方法和规则网格有限差分法进行模拟。图7为利用两种方法模拟的0.15 s时刻的波场快照，可以看出，本文方法能够有效压制边界处阶梯状网格引起的虚假散射波。图8为利用本文方法模拟的直达波在（500 m，600 m）处的单道地震记录与黏弹解析解及弹性波解析解的对比，可以看出，本文方法的数值解与黏弹解析解完全吻合，且与弹性波解相比振幅明显衰减。

图8 本文方法模拟的直达波与黏弹解析解及弹性解析解的对比

3.2 起伏地表多层介质模型

为了测试本文方法对起伏地表模型的适用性，建立了起伏地表两层和三层黏弹介质模型（图9），各层参数如表1所示。采用与起伏地表均匀模型相同的方法对起伏地表两层和三层模型进行网格剖分（图6b，地形相同，网格剖分相同）。

表1 起伏地表多层介质模型参数

图9 起伏地表两层（a）和三层（b）黏弹介质模型

以主频为75 Hz 的Ricker 子波作为震源，位于（500 m，5 m），图10和图11分别为两层模型本文方法模拟的0.20和0.25 s时刻的波场快照。由图可见，地震波在传播到山峰和山谷的拐点时都会产生强烈的散射波和绕射波，且发生面波和体波之间的相互转换，散射面波的能量要强于散射体波；当地震波传播到界面时会产生反射波、透射波和转换波。图12为三层模型本文方法模拟的两分量单炮记录。从图中可以观察到起伏地表拐点处产生的强烈散射波和两个介质分界面上的反射波、转换波。由于地层界面是崎岖的，因此反射波同相轴发生了畸变，不再是以炮点为中心的双曲线。起伏地表两层和三层黏弹介质模型计算结果表明本文方法对复杂模型同样有较强的适用性。

图10 两层模型本文方法模拟的0.20 s 时刻的波场快照

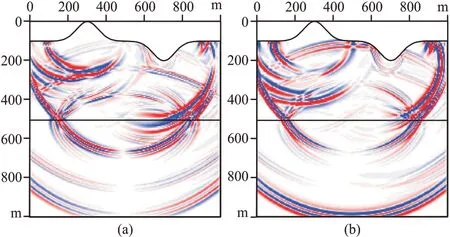
图11 两层模型本文方法模拟的0.25 s 时刻的波场快照

图12 三层模型本文方法模拟的单炮记录

4 结论

地震波数值模拟是研究地层中地震波传播规律的有效方法。本文采用改进的RL 正交贴体网格生成方法对起伏地表下的黏弹性介质进行网格剖分，并利用优化的选择性滤波同位网格有限差分法模拟曲线坐标系下的一阶速度—应力方程。数值算例表明：

（1）改进的RL 算法能够对起伏地表模型进行精确的正交贴体网格剖分，从而有效消除阶梯状网格引起的虚假散射波；

（2）网格的正交性使得在实施自由边界条件时无需做复杂的坐标转换和插值运算，从而有效提高了模拟精度；

（3）因为二维和三维使用的是相同的差分格式，所以本文算法很容易向三维推广。