常见公路拓宽路基的稳定性分析方法
王剑英,王天成
(1.黑龙江工程学院 土木与建筑工程学院,黑龙江 哈尔滨 150050;2.哈尔滨职业技术学院建筑工程与应急管理学院,黑龙江 哈尔滨 150076)
0 前 言
早期的高速公路由于对未来交通量的预测不够准确,同时受当时社会经济条件、施工技术水平、设计理念等因素影响,大部分高速公路按双向四车道建设,随着我国经济的飞速发展和车辆保有量的迅速提高,很多早期修建的高速公路无法满足当前的交通量[1,2],公路改扩建是解决这类问题的有效方法,同时拓宽路基稳定性也成为广大学者研究热点。本文以高速公路四车道改建为六车道为例,分析拓宽路基稳定性。原有路基宽度26 m,改建路基宽度34.5 m,采用双侧加宽,每侧需增加4.25 m宽度,其中土路肩宽度0.75 m,硬路肩宽度3 m,假设硬路肩边缘作用一车辆荷载,荷载大小25 kPa[3]。
高速公路路面结构型式、结构层力学指标,拟定如表1[4,5]。路基填料为碎石土,地基为粉质粘土。以8 m高路基为例,分析路基稳定性。
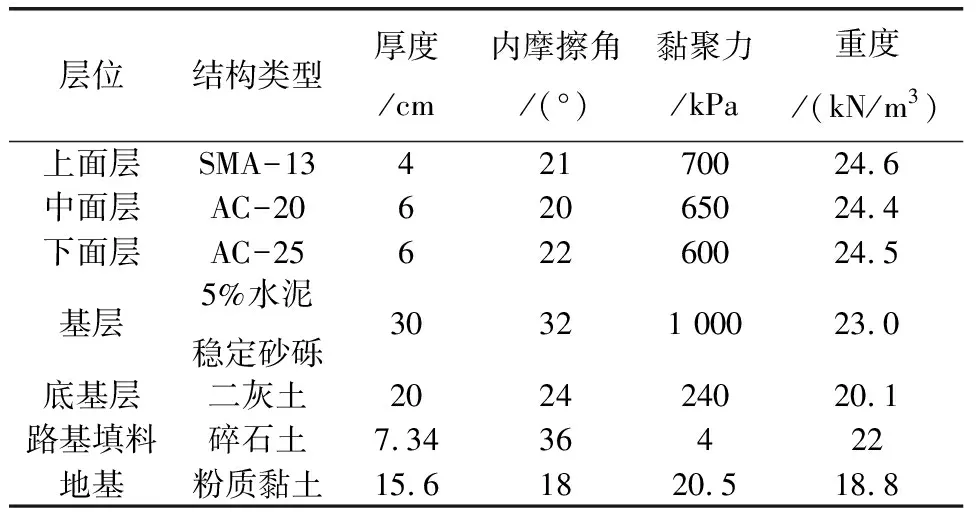
表1 高速公路路面结构型式
1 应用理正深基坑软件7.0分析路基稳定性
新旧路基结合良好,成为一个整体,没有差异沉降,路面面层没有开裂,如图1。
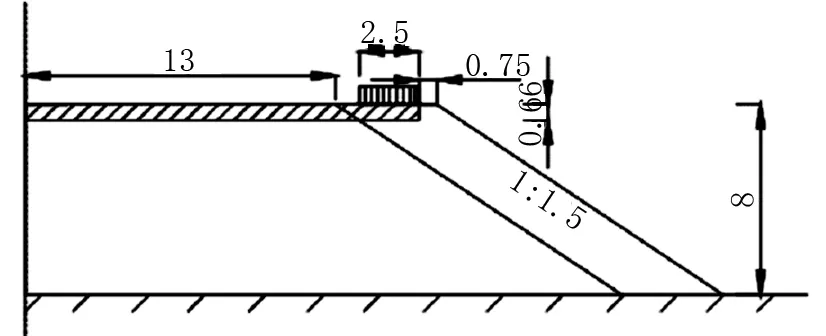
图1 拓宽路基示意图
应用理正深基坑软件7.0找到最不利圆心及滑动圆弧半径,此种情况最不利圆弧位于坡面上,如图2,最不利圆心及半径见表2(圆弧序号3),坐标原点(0,0)位于坡脚。
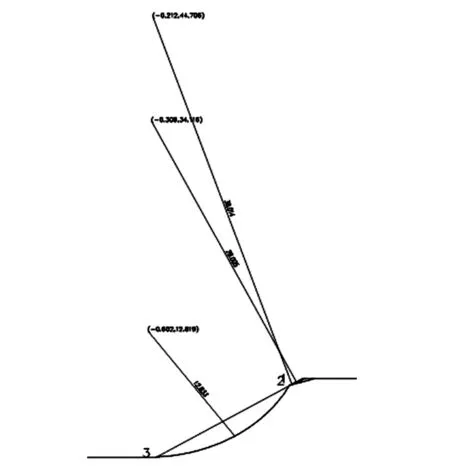
图2 最不利圆心及滑动圆弧半径
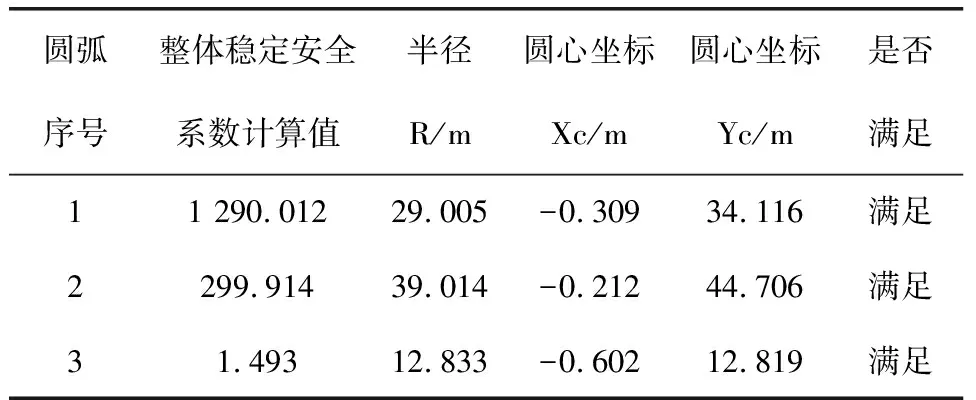
表2 滑弧圆心及半径
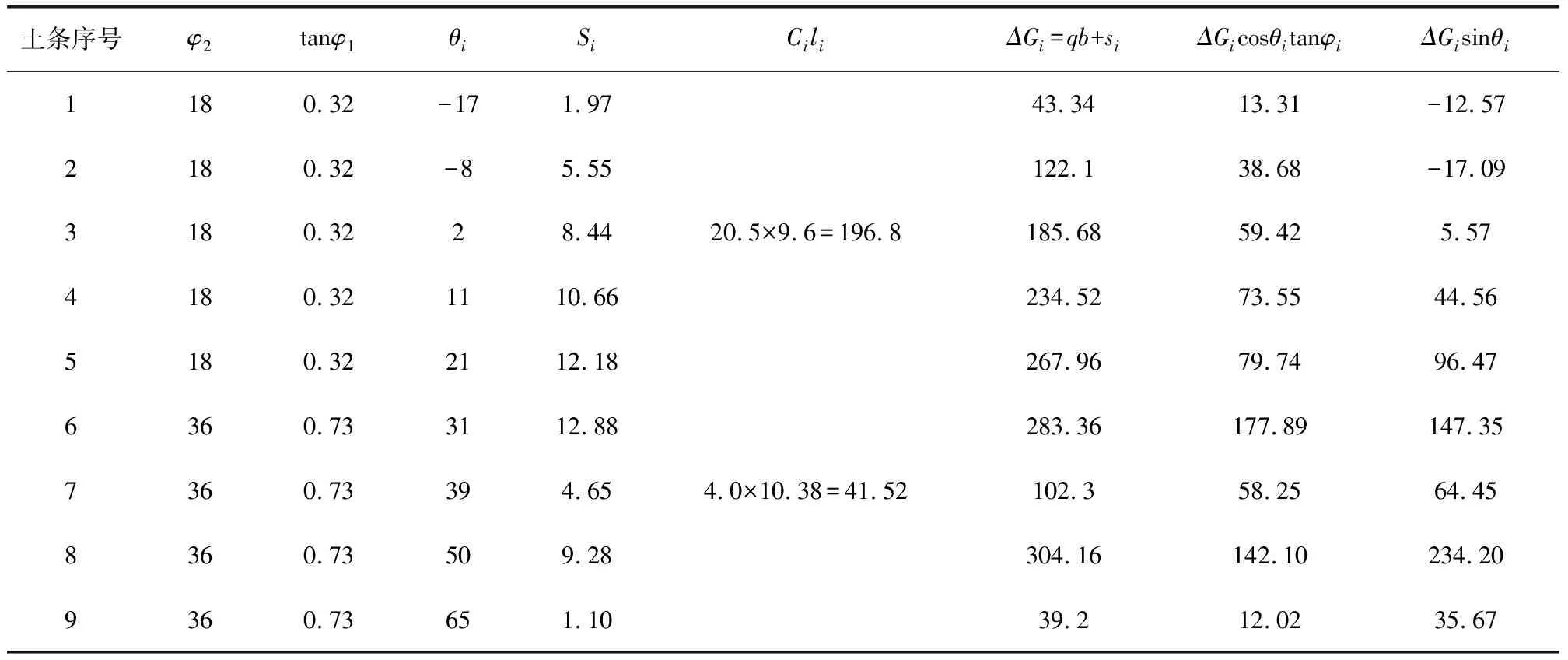
表3 土条计算指标
通过计算得出此边坡最小稳定系数Kmin=1.493大于1.25,所以边坡稳定。由于路面面层没有开裂,面层、基层抗剪强度高,不会发生贯穿路面结构层的破坏,因此稳定系数最小的滑动面在边坡坡面部位。
2 条分法分析边坡稳定性
新旧路基结合良好,但存在差异沉降,路面面层开裂,如图3,假设此时面层的抗剪强度为零,滑动圆弧通过路面结构层底新旧路基结合处,并且通过坡脚,圆心在36°线上,如图。采用条分法[6,7],利用公式1计算边坡稳定性。
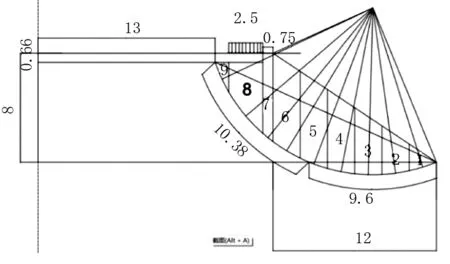
图3 条分法计算示意图
(1)
式中:k为边坡整体稳定安全系数;ci、φi为第i个土条滑动面上的粘聚力、内摩擦角,(kPa、°);Si为第i个土条的面积;ΔGi为纵向取1延长米第i个土条的重量(包括土条范围内的路面及荷载),kN;θi为第i个土条滑弧中点切线与水平面的夹角,即法线与竖直面的夹角;li为第i个土条在滑动面上的滑弧长度。
通过1、2两种情况对比,Kmin=1.493和Kmin=1.492,发现路面开裂对路基稳定性的影响并不大,说明路基的稳定性决定了路基路面的稳定性。
3 不平衡推力法分析边坡稳定性
新旧路基结合不良,产生差异沉降,路面面层开裂,并已断开,新建路基可能会沿原边坡表面和原地面滑动,采用不平衡推力法,应用公式2、3分析路基稳定性[8],如图4。
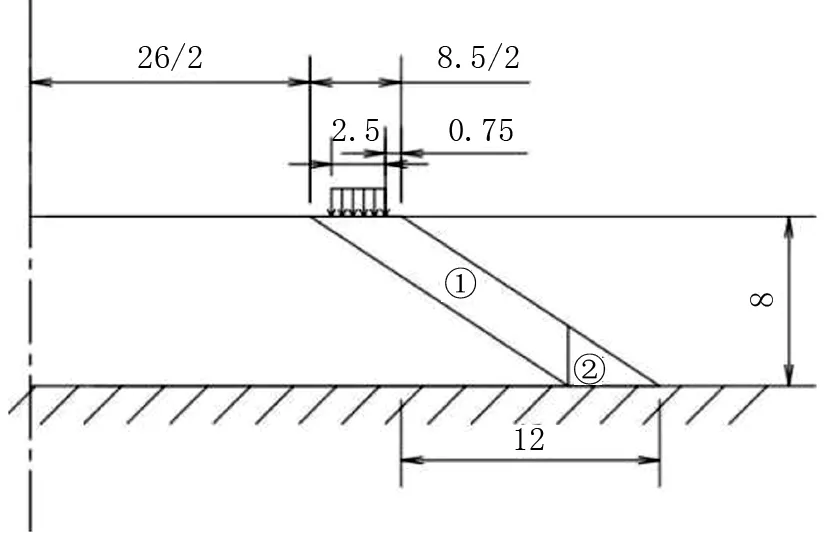
图4 不平衡推力法计算示意图
将滑动土体按滑动面坡度分为两部分,计算参数如表4,为简化计算,加宽路面结构层厚度0.66 m范围内的重度用路基填料重度代替,为提高安全度,假定路基填土与地基之间的粘聚力为零。

表4 滑体计算指标
(2)
E2=E1cos(α1-α2)-
(3)
式中:K为安全系数取1.25;ci、φi为第i个滑动土体的粘聚力、内摩擦角,kPa、°;si为第i个滑体的面积;Gi为纵向取1延长米第i个滑体的重量(包括滑体范围内的路面及荷载),kN;αi为第i个滑体滑动面倾角;li为第i个滑体滑动面长度;Ei为第i个滑体的剩余下滑力。
经计算E1=4.86,E2=-30.98,第二个滑块的剩余下滑力E2为负值,说明路基边坡稳定。
从计算结果分析,第一块滑体的剩余下滑力已经大于零,说明第一块滑体不稳定,如果原地面横坡变陡,或雨水从裂缝渗入导致路基填土或原地面抗剪强度变低,路基有失稳的可能性。
4 结 语
本文介绍了拓宽路基稳定性分析的方法,应用理正深基坑软件7.0、条分法、不平衡推力法等路基稳定性分析方法,并附详细计算过程,由于本人学识有限,不当之处敬请同行指证。

