基于深度神经网络的短波特定信号识别研究*

王 鹏，黄伟强

（广州海格通信集团股份有限公司，广东 广州 510663）

0 引言

短波天波通信是典型时变色散信道，不仅具有多径延时、衰落、多普勒频移等特性，其接收信号的信噪比等参数也是实时变化的。此外短波信号种类繁多，各信号间有一定的相似性，这都对短波特定信号的识别造成了较大影响。

短波特定信号识别实质上是典型的模式识别问题，即首先通过对信号样本进行预处理实现信号特征提取，其次通过特征统计和比对实现特定信号识别。特定信号的识别方法大致可以分为时域匹配法[1]、频域匹配法[2]和时频域匹配法[3]3 类。目前，已有很多研究结合时频分布图像，利用图像增强、图像分割、形态学去噪等图像处理方法对信号进行检测和识别[4-9]，但在低信噪比和信道强干扰情况下效果欠佳，提取的特征不能很好地表征受信道强干扰的信号。近年有研究利用独立卷积神经网络（Convolutional Neural Networks，CNN）、双向长短时记忆（Bi-directional Long Short Term Memory，Bi-LSTM）网络[10-11]和深度神经融合网络[12-13]将同相正交（In-phase/Quadrature，I/Q）信号作为序列处理来识别调制种类，在I/Q 信号序列较长时识别概率较高。还有研究利用I/Q 信号序列同时识别调制方式和信道编码类型的方式来识别信号种类，这种方法在信号质量较好时取得了良好效果[14]。

本文基于短波信号本身的帧特征，使用CNN、LSTM 和注意力机制搭建深度神经融合网络模型对短波基带信号直接进行检测识别。

1 短波波形识别建模

根据短波天波传播特性可知，其信号帧结构中都含有同步帧和发射电平起控帧，如图1 所示。同步帧（也称为报头帧）是指在信号发送的帧结构数据中一段具有特定规律的数据码，一般在数据帧的前面部分，起到帧同步、符号同步、载波同步等作用。发射电平起控帧用来抵消功放功率上升时间，以保证同步帧可以满功率输出。

图1 短波信号帧结构

不同种类的短波信号的同步帧也不同。相同同步帧在不同调制方式下的特征图呈现出不同的特性，然而即使在相同调制方式下，相同同步帧若具有不同的数据帧结构也会产生不同的特性。因此，本文提出一种基于同步帧注意力机制的卷积神经网络结构，用于特定信号类型的识别。

1.1 一维卷积神经网络

相比于传统的二维基带I/Q 波形，利用一维基带信号进行特征处理的运算量更低。因此本节构造了尺寸相对较小的一维卷积模块对一维波形的短波信号结构信息进行提取，以降低计算成本，并在堆叠后实现了高效的特征提取。

设接收的短波信号波形序列为{X(n):n=1,…,N}。在第一个卷积层中，构造的K个尺寸为M的一维卷积核可表示为{Wkm:m=1,…,M,k=1,…,K}，则该层有N个输入节点和K个输出特征序列，其中，Wkm为第m个输入节点和第k个输出特征序列之间的连接权值，又设bk为第k个输出特征序列对应的偏置值，那么，第k个输出特征序列是输入序列的一维非线性卷积变换，可表示为：

式中：f()为非线性激活函数，一般选用ReLU 函数。类似于二维卷积，一维卷积在计算同一个输出特征序列时采用相同的连接权值来减少参数数量，且每次卷积仅取部分输入节点进行运算，即通过局部连接和参数共享来提高特征提取的效率和质量。经过第一个一维卷积层后，输出的K个特征序列集合为[S1=S1l,…,Skl]，[Sk=Skl,…,SkN]，k=1,…,K。之 后，利用尺寸为1×q的一维最大值池化对每个特征序列进行降维操作，得到新的特征映射矩阵。最后，再将多个卷积层堆叠形成级联结构，构建深度卷积网络对输入的结构特征进行层次化变换提取。

1.2 双向长短记忆网络

LSTM 对时间序列的预测只与前向时间段的信息相关，而在实际的短波信号时序数据集中，对一时段的信号数据预测不仅受到前一时刻序列的影响，而且后向时段的数据特征变化也同样能够影响当前时段的模型输出。双向连通的Bi-LSTM 网络是由两个上下反向叠加的单向LSTM 连接组成，模型输入包含预测时间之前和之后的时间序列，因此能够同时处理正向和反向的时间序列数据。Bi-LSTM网络结构如图2 所示。图中，ht和ht'分别指代t时刻的向前和向后向量，yt为输出序列。W1～W6为各层网络之间信息连接的权重矩阵。

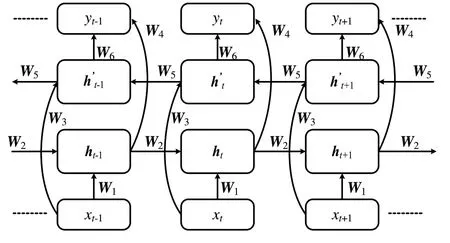
图2 双向Bi-LSTM 网络结构

1.3 基于残差网络的注意力模块

为了学习更加具有判别性的局部同步帧特征，在残差网络的基础上引入卷积块注意力模块，即在每个残差block 中插入注意力机制，具体做法如图3 所示，在原来输出的特征图之后，分别插入通道注意力模块，然后插入空间注意力模块。

图3 基于注意力机制的残差网络

基于同步帧注意力机制的卷积神经网络结构依次使用通道注意力模块和空间注意力模块得到特征图，因此模型可以分别在通道和空间上学到帧同步头的位置及特征。

注意力机制特征优化原理如图4 所示，将样本标签表示为Yi，将故障特征表示为Ki，Ki={Ki1,Ki2,…,Kij}，其中，i表示不同的样本，Kij(j=1,2,…,n)为j个不同特征。通过全连接神经网络计算由每个特征Kij所得到的特征权重参数Wij，用来表示由Kij所得的目标值Yij与Yi的相关性，并经过Softmax 归一化处理，得到所有特征权重和为1 的概率分布，并对原始特征Kij进行加权，得到优化后的特征矩阵。

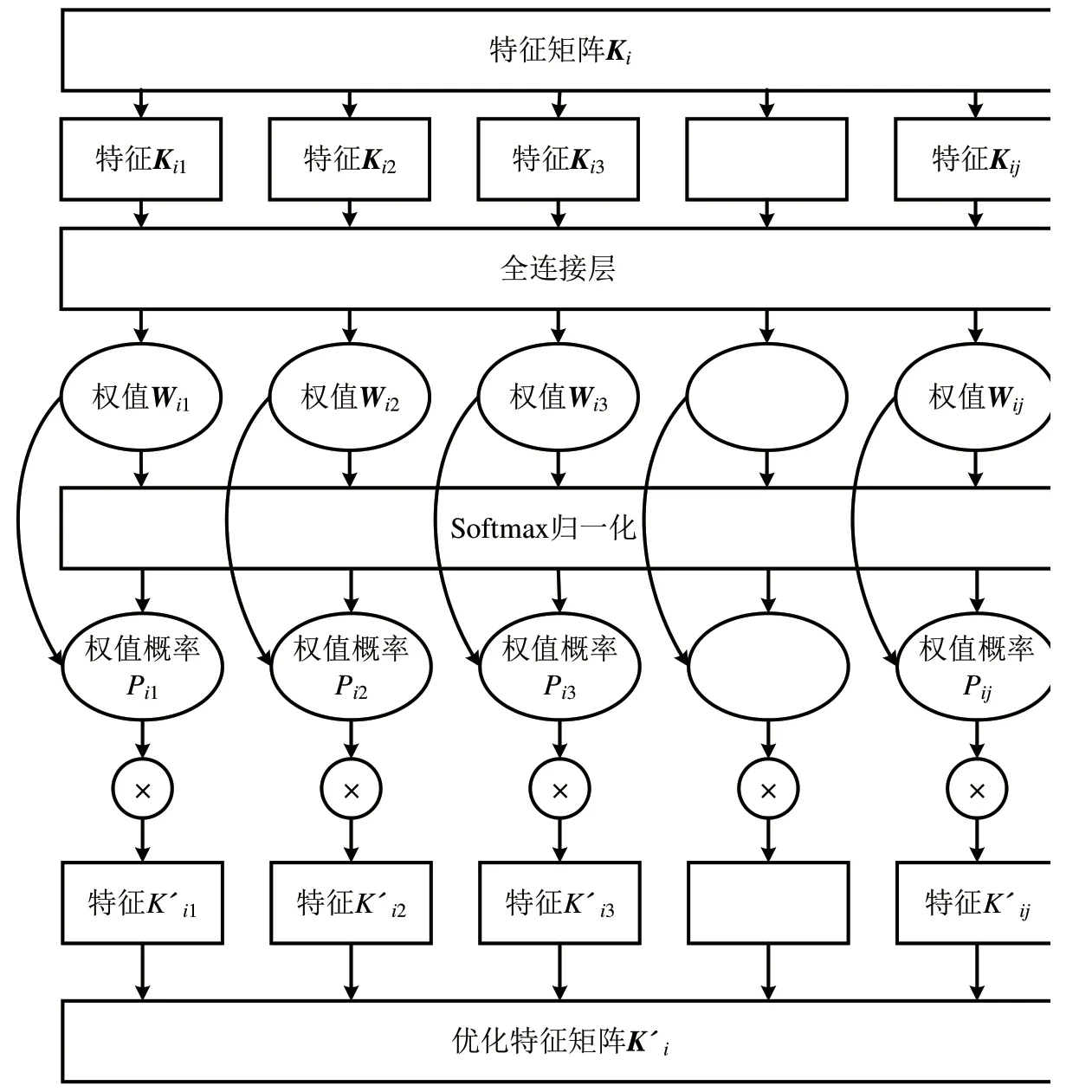
图4 注意力机制特征优化原理

1.4 短波特定信号识别模型

在模型设计上，基于CNN、LSTM 和注意力机制搭建深度神经网络模型。使用该模型，经过3 层全连接层后的输出结果是对输入的短波数据的信号种类的最终预测，如图5 所示。

图5 结合CNN、LSTM 与注意力机制结构

首先，将短波信号进行预处理之后输入卷积层得到的每帧的高级表征拼接成时间序列数据，并交给LSTM 来处理。

其次，使用注意力池化层，根据LSTM 的输出（Hidden State）来计算权重并归一化，将权重系数与LSTM 的输出矩阵相乘作为全连接层的输入信息，通过加权求和的方式，就能很好地抓住与上下文相关的部分。而从接收的实际信号看，信号中TLC 部分由于功放的起控时间慢不能全部发出来，即接收到的信号起始符号不完全一致，因此尝试把LSTM替换成双向的（Bidirectional）LSTM，它可以被看作是两层LSTM，一层从信号起始点开始输入，一层从信号末端开始输入，在t时刻分别保存两个状态值At和，最终该时刻的输出（hidden state）由两个状态值共同决定，这样就联系了信号的上下文信息。

再次，在注意力层其实是引入了一个外部的权重得分，对LSTM 或Bi-LSTM 中每个时刻的输出做了一个重要度评分。由于这里LSTM 和Bi-LSTM 的本质还是对时间序列数据提取出高级特征表示，而不是实现所有的帧级别（frame-level）的特征对信号种类识别都有同样的贡献，因此注意力机制是帮助寻找哪些时刻的输出（hidden state）是强特征，从而得出一个高层的具有判别性的表征，使得模型专注于重要的部分。

最后，把这些高级表征传入一个含有512 个节点的全连接层，通过几层全连接层来进行最终的决策识别。

2 识别实验结果及分析

2.1 实验数据集

选择Codan 16 音[15]（C16）、XK852[16]（X5）、Mil-Std-188-110A[17]（MS110A）、Link11A Clew[18]（LC）、Link11A Slew[18]（LS）这5 种典型信号的真实样本，进行信号种类的识别。

（1）MS110A、XK852、Link11A Slew。这3 种信号属于串行单音，其载波频率均为1 800 Hz，调制方式同为8PSK，符号率为2 400。XK852 与Link11A Slew 的发射电平起控帧（TLC）和同步帧相同，MS110A 的发射电平起控帧（TLC）和同步帧与XK852、Link11A Slew 不同。这3 种信号的空口接收后的时频图如图6、图7 和图8 所示。

图6 Link11A Slew实际信号时频图

图7 XK852实际信号时频图

图8 MS110A 实际信号时频图

（2）Codan 16 音和Link11A Clew。Codan 16 音是并行多音信号，其两个相邻的子载波间隔为112.5 Hz，共16 个子载波。Link11A CLEW 也是并行多音信号，14 个相邻的子载波间隔为110 Hz、605 Hz 和2 915 Hz，共16 个子载波。这3 种信号的空口接收后的时频图如图9、图10 所示。

图9 Codan 16 音实际信号时频图

图10 Link11A Clew 实际信号时频图

采集整理并标记这5 类实际信号样本，样本数量如表1 所示。

表1 5 类信号样本的数量

实际信号被采集后，其数值范围分布差异很大。为了更好地适应深度学习网络模型的计算，需要对信号进行预处理，主要包含：

（1）约束输入长度处理：实际信号的采样率为9 600 波特，为与同步帧长相匹配，模型输入长度设定为2 000 个样点。

（2）信号归一化：本文选取了0 均值标准化，输入Xin与输出Xout之间的关系为：

式中：μ为输入序列的均值；σ为输入序列的标准差。

2.2 训练结果分析

首先为了对比融合网络的效果，设置了5 个对照实验：第1 个是去除注意力层和LSTM 层，仅使用CNN 神经网络模型，将CNN 提取的特征经过一个全局平局池化层之后输入3 层全连接层中；第2个是去除了卷积层和注意力层，仅使用LSTM 的神经网络模型，将LSTM 的最后时刻的状态向量输入3 层全连接层中；第3 个是去除了注意力层，仅使用CNN+LSTM 的神经网络模型，将LSTM 的最后时刻的状态向量输入到3 层全连接层中；第4 个和第5 个都是使用结合了CNN、LSTM 和注意力机制的网络，第4 个使用的是LSTM 网络，第5 个使用的是Bi-LSTM 网络。

实验使用了Dropout、Early Stopping 等手段防止模型过拟合，并使用均方误差作为损失函数。此外，在实验中为了避免随机性影响结论的稳定性，每次模型测试都进行了10 次交叉验证。

采用不同的网络结构对信号种类数据集进行训练，得到了不同网络结构训练和验证的损失值曲线，如图11 和图12 所示。图中横轴表示训练的周期数，纵轴表示损失值的大小。从图中可以看出，不管是训练集还是测试集，结合CNN、LSTM 和注意力机制网络的拟合效果都是最好的，主要表现为更小的损失值。而仅使用LSTM 网络的拟合效果最差。

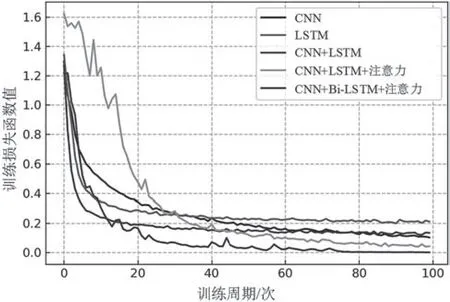
图11 不同网络的训练损失函数对比

图12 不同网络的验证损失函数对比

不同网络的训练准确率如图13 和图14 所示。可以明显看出，CNN+LSTM 结合注意力机制的模型在各个评价指标上都比仅使用CNN 或LSTM 的模型表现好很多。最终的训练结果是CNN+Bi-LSTM 结合注意力机制的模型对5 种信号达到了99%的识别准确率。

图13 不同网络的训练准确率对比

图14 不同网络的验证准确率对比

2.3 测试结果分析

图15 显示了5 种不同的模型对测试样本的识别准确率的混淆矩阵。图中横轴表示模型的预测类别，纵轴表示输入信号的真实类别，对角线代表每个信号种类对测试集的平均识别准确率。

图15 不同网络模型的测试准确率对比

从图中可以看出，5 种模型对Link11A Clew 的识别准确率都很高，基本没有和其他类型混淆，这是因为Link11A Clew 的信号结构与其他信号种类的差别很大。除了CNN+Bi-LSTM+注意力模型，其他模型对Link11A Slew、MS110A 和XK852 的识别效果都相对较差，且错误识别的样本都存在相互混淆，这是因为串行单音PSK 调制信号区分没有并行信号之间那么明显，且由于Link11A SLEW 与XK852 的同步帧相同，仅后面数据部分有差异，因此采用Bi-LSTM 的模型识别效果更好。5种模型对5 种信号（未参加训练）的识别准确率如表2所示。

表2 不同模型的平均识别准确率

从表2 可以看出，CNN+Bi-LSTM+注意力模型对5 种信号种类的平均识别准确率达到了0.984，高出单一模型2%～6%。

3 结语

本文探索了基于深度神经网络的短波特定信号识别技术，设计了适用于处理基带信号的结合CNN、LSTM 和注意力机制的神经融合网络模型。最后，采用实际信号的训练样本和测试样本，对不同的融合网络进行训练，并用不同地理位置上的短波信号测试集进行测试验证，训练好的模型达到了预期的目标。本文所提技术相较于传统短波信号种类识别算法，不需要人为提取信号的特征，计算复杂度相对较低，鲁棒性相对更高。