扩频信号检测技术综述*

王在昌，程 剑，苏荣辉

（1.中国人民解放军陆军工程大学，江苏 南京 210001；2.中国人民解放军73636 部队，福建 福州 350000）

0 引言

扩频通信信号是最早提出的低截获设计信号形式，具有功率谱密度低、抗干扰能力强、隐蔽性能好、抗多径等优点，能够在低信噪比条件下实现可靠通信，且具有良好的抗截获性能，广泛运用于通信、雷达、导航、数据链等各种军事通信系统中。随着技术的进步，逐步发展出跳频、跳码、非周期扩频、大扩频比混沌序列扩频、变载波频率扩频、线性调频等信号，使得当前军事通信信号隐蔽性得到极大提高。

信号检测是指对接收的一段信号利用信号概率和噪声功率等信息按照一定的准则判定信号是否存在，是实施通信侦察的基础，也是进行通信信息截获、干扰与情报提取的关键前提。而由于扩频技术的发展，传统检测方法的性能急剧下降，对信号进行检测变得更加困难。面对更加复杂多变的通信环境和日趋严峻的军事对抗形势，实现高效、准确、快速的信号检测是掌握军事信息对抗主动权、抢占信息制高点的基本前提，是提高信息化作战能力、打赢现代战争的重要保障，是当前和今后一段时期信息化作战研究领域的重要课题。因此，开展信号检测技术的研究工作具有重要意义。

1 扩频通信研究现状

扩频通信是扩展频谱（Spread Spectrum，SS）通信的简称，是指用来传输信息的信号带宽远远大于信息本身带宽的一种传输方式[1]。扩频通信最早用于军事通信中，它通过扩展通信信号的带宽来达到将信号隐藏在信道噪声中的目的，由此增强军事无线通信信号的隐蔽性和保密性。扩频通信的基本工作方式有直接序列扩频（Direct Sequence，DS）、跳变频率（Frequency Hopping，FH）、跳变时间（Time Hopping，TH）、线性调频（Chirp Modulation，Chirp）4 种。此外，还有采用以上两种或两种以上工作方式的混合扩频形式，如跳扩（FH/DS）、TH/DS、多进制扩频等，近些年又逐步发展出软扩频技术、多进制正交扩频、可变速率通信等扩频形式。

1.1 直接序列扩频

直接序列扩频（Direct Sequence Spread Spectrum，DSSS）是最早发展起来的扩频技术，也是现代扩频技术的基础。直接序列扩频通过将待传信源信号与扩频码相乘得到扩频信号，使信号在时域上周期变小，从而达到在频域中频谱展宽的目的。下面以BPSK/DSSS 调制为例介绍直扩的具体调制解调过程，其系统原理如图1 所示。

图1 BPSK 调制直扩系统原理

直扩信号模型为：

式中：P为信号的功率；d(t)∈{-1,1}为信息数据序列，信息码元宽度为Tb；c(t)∈{-1,1}为扩频序列，扩频码元宽度为Tc；f0为载频，φ为载波初相；n(t)为零均值高斯白噪声。直扩调制采用常规短码扩频方式，生成复合码序列时一个扩频码周期对应一个信息码长度，即Tb=pTc，其中，p为扩频码长。

系统的抗截获和通信质量等性能都与系统所用的扩频码的性能相关。要想实现较好的通信效果和低截获性能，扩频码应具有如下特点：有足够多的扩频序列，尽可能大的序列复杂度，尽可能小的互相关性，尽可能尖锐的自相关性，还要工程易于实现等。常见的扩频码有m 序列、Gold 序列、M 序列、Walsh 序列、OVSF 序列、Kasami 序列等。

随着扩频技术的发展，罗卫兵提出了一种多电平扩频码进行连续相位调制，在调制带宽不变的条件下，解决了传输信号容易被平方检波器和比特延迟检波器侦测的问题[2]。为进一步提高频带利用率和信息传输效率，此后方旭又提出并行组合扩频、码索引调制技术和时移位置调制等方法[3]。

随着混沌系统的提出，使用混沌序列取代PN 码作为扩频码的直扩通信系统得到进一步发展[4]。常用的混沌序列产生方法有Logistics 映射、Chebyshev 映射及Tent 映射等方法。混沌序列的应用使码元间具有较好的低相关性，进一步提高了系统的保密性与安全性。文献[5]通过对混沌序列进行加权分数阶傅里叶变换（Weighted Fractional Fourier Transform，WFRFT），进一步增强了混沌直扩通信系统的抗截获性。

1.2 跳 频

利用扩频码对发送信号的载波频率进行跳变控制的扩频方式称为跳频扩频。与直接序列扩频不同的是，这种扩频方式是让载波频率在一定范围内规律性跳变，进而展宽传输信号的带宽，而不是对信息码频谱进行扩展[6]。跳频扩频受远近效应影响小、对抗跟踪式干扰的能力强，且跳频频率的数目越多，跳速越高，系统的抗干扰性能也就越好[7]。

瑞典学者J.Zander 于1995 年提出自适应跳频通信，之后，在军事通信和蓝牙系统等慢跳速系统中得以成功应用，大大提高了无线通信系统的抗干扰性能。目前，自适应跳频技术正由慢速跳频向快速跳频方向发展[8]。为达到避开频率集之中被干扰的频点的目的，杨晓文提出基于概率的自适应跳频通信，进一步提高了系统抗干扰性能[9]。为对抗“灵巧式”干扰，严季提出变跳速、变间隔跳频通信[10]。

由于跳频序列的设计是跳频通信的核心技术，对扩频码的研究也逐渐深入。由m 序列扩频码发展出采用具有良好初值敏感性的混沌映射构造跳频序列，例如，文献[11]提出了改进的4 分段Tent 混沌映射，文献[12]提出一种混沌多音调调制解调技术，文献[13]提出将Logistic 混沌映射序列作为卫星导航信号扩频码，利用构造的组合混沌映射产生跳频序列控制导航信号发射频率的跳变，进一步增强了跳频通信的性能。文献[14]提出用混沌序列来控制卫星通信系统的跳频和跳码，文献[15]设计了一种基于混沌标准映射（Chaotic Standard Map，CSM）的低截获概率跳频图案，文献[16]提出基于随机跳频的保密通信系统，都能有效提高系统的低截获性能。

1.3 线性调频扩频

线性调频（Linear Frequency Modulation，LFM）扩频，又称Chirp 扩频，与传统扩频技术的区别在于无需伪随机扩频码，仅利用其自身的线性频率特征，具有信号处理增益高、抗干扰能力强、多普勒容限较大等优点。线性调频的频率与时间呈线性关系，用信号的频率变化率来表示发送信息，常用Chirp-BOK 调制。为了提高发送波形的LPD 性能，文献[17]提出将调制信号等时宽模式扩展为变时宽模式，即变时宽Chirp 率调制（VT-CRM）方式。文献[18]结合跳频与跳时的设计思想，提出一种由PN序列控制的多波形基Chirp扩频（Multi-Waveforms Chirp Spread Spectrum，MW-CSS）通信方案，提升了系统隐蔽性能。

1.4 跳 扩

直接序列扩频与跳频扩频是最为常见的两种扩频方式，且都具有很强的抗干扰能力和隐蔽性能，但是两种扩频方式也各自存在不足，单独使用其中一种扩频方式很难使系统满足各种应用场景的需求。将两种或两种以上的扩频技术合理地结合起来组成新的扩频方式能够极大地提高扩频系统的综合性能。直接序列－频率跳变的混合扩频通信系统（DS-FH）是最常用的混合扩频系统，美军战术数据链正是用的此种扩频方式。

传统的跳扩信号采用了固定通信参数设计，在通信信号波形及其参数域中引入循环平稳特征，为非合作截获方通过统计分析获取通信参数提供了突破口，针对传统扩跳频通信信号的这一固有弱点，研究者们提出了基于变参数的跳扩通信技术[19]，提高了系统性能。

1.5 其他扩频方法

软扩频技术（Tamed Spread Spectrum），也叫作M 元扩频、缓扩频，它的频谱变换是一个缓慢变化的过程，该技术是将编码技术与直接序列扩频技术有机结合而演变出新一代基带扩频技术[20]。文献[21]提出了一种基于单向耦合映像格子（One-way Coupled Map Lattice，OCML）模型的时空混沌序列的缩短码移位键控（OCML-TCSK）技术，利用改进型logstic 映射的不变分布特性生成混沌伪随机序列，并采用镜像对称的方式，在保证传输信息量相同的条件下，缩短了原扩频序列的码长，提高了系统的传信率。

此外，二进制偏移载波（Binary Offset Carrier，BOC）调制[22]、双通道轨道角动量（Orbital Angular Momentum，OAM）扩频系统[23]、滤波器组多载波扩 频（Filter-Bank Multi-Carrier-SS，FBMC-SS）[24]等新技术的提出更增加了信号检测的难度，亟须研究性能更好、鲁棒性更强的检测方法和技术。

2 扩频信号检测技术研究现状

经过多年的研究发展，发展出多种针对扩频信号的检测算法。根据对扩频信号不同特征的检测特点，如图2 所示，将检测算法分为5 类，分别是：基于能量的扩频信号检测、载波频率检测、扩频码周期检测、扩频码速率检测和其他检测法。上述介绍的低截获技术的运用使得通信信号的检测变得更加困难，常规的检测方法可能不能取得很好的检测效果，需要根据相应的技术提出相对应的检测方法。

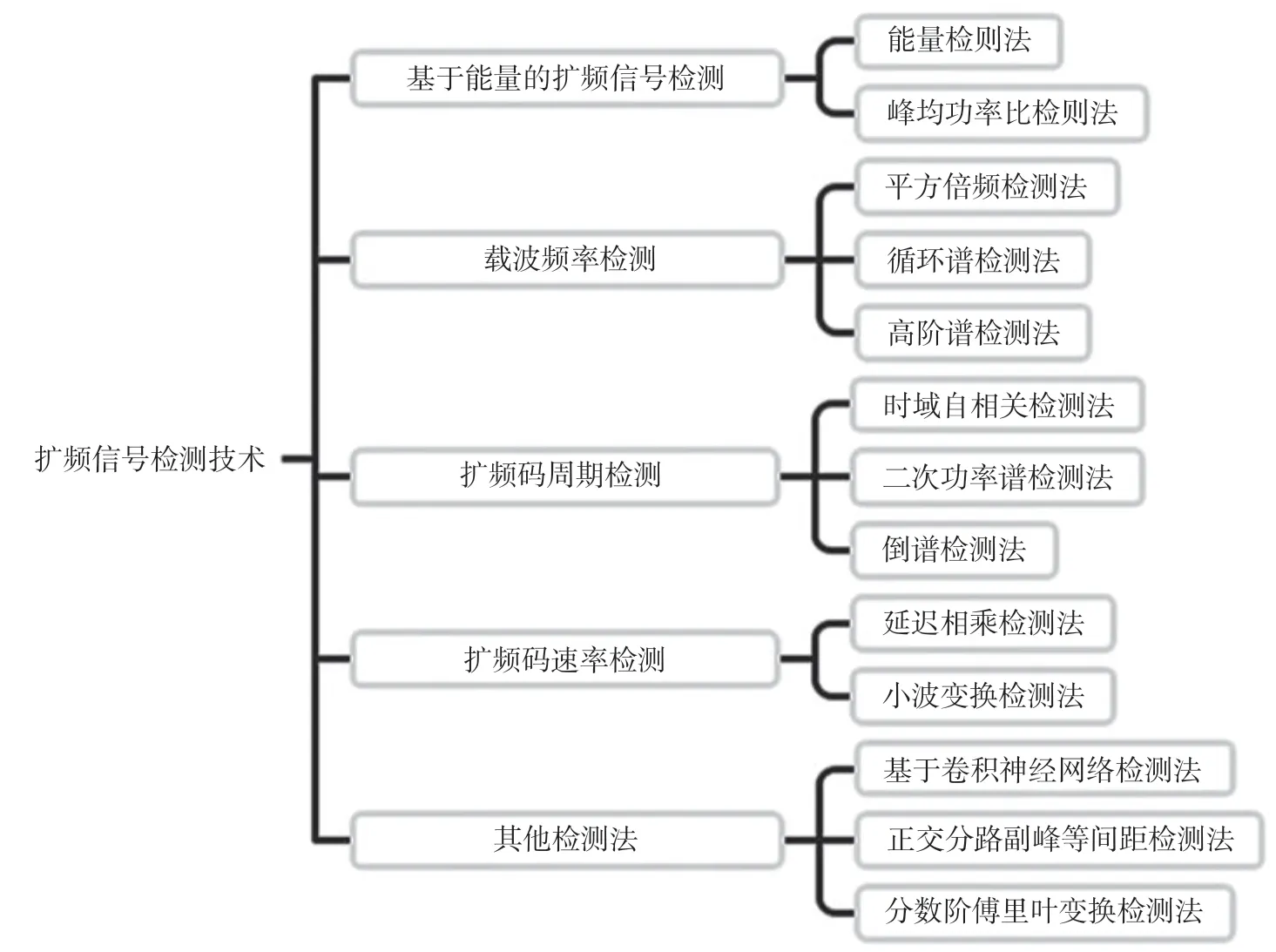
图2 扩频信号检测方法

2.1 基于能量的扩频信号检测

2.1.1 能量检测法

能量检测法[25]是针对低截获信号的最基础的检测手段，其理论依据为：在高斯白噪声环境下，当待检测信号存在时，信号与噪声的能量总和大于仅有噪声时的能量，即通过观测信号是否存在的两种假设条件下接收机收到的信号能量幅值差异，来解决的信号检测问题，故找到了合适的判决门限就能检测信号的有无。在背景噪声平稳且没有干扰的情况下，能量检测法的性能较好，且易于实现。但当背景噪声非平稳或背景噪声远大于信号时，很难确定合适的检测门限，其检测性能急剧下降。因此采用能量检测法对直扩信号进行检测，检测性能很差。

2.1.2 峰均功率比检测法

文献[26]提出基于信号峰均功率比（Peak to Average Power Ratio，PAPR）的直接序列扩频信号检测算法，该算法通过计算信号的峰均功率比，并将峰均功率比的平均值作为检验统计量，实现扩频信号的检测。该算法克服了能量检测法存在信噪比墙的缺点，在保证较低计算复杂度的同时，表现出较好的检测性能。

2.2 载波频率检测

2.2.1 平方倍频检测法

常见信号的相移键控调制方式是用不同的相变来表征信息的，而经过平方则能够消除这些相变。例如，对于BPSK 调制方式，信息码主要反映在0和π的相变上，经过平方倍频处理，这种相变就被消除了，信号就变成含有载频的二倍频的简单形式，对其进行傅里叶变换会在二倍载频位置出现明显谱峰。该算法在检测信号的同时能够估计出信号载频，但其缺点是只适用于一定的调制方式。

接收信号x(t)经平方后，其结果为：

平方－相关累积法[27]是平方法的一种改进，在平方倍频法的基础上，将相关累积技术应用到平方倍频法中。根据噪声的不相关和正弦信号的相关特性，可对平方后的信号进行自相关，谐波信号相关后的结果仍然是一个同频率的谐波信号，再在相关域做积累，这样大大提高了抗噪声检测能力。

2.2.2 循环谱检测法

由于一般直扩信号都具有周期平稳特性，而噪声没有周期平稳特性，因此循环谱检测法通过计算接收信号的循环谱密度函数来检测是否存在直扩信号。该算法是对功率谱的一种推广，增加了用于分析信号的信息，并且由于信号和噪声的循环谱特点，使得该算法有着很好的抗噪声和抗干扰能力。但是，该算法计算复杂度高，计算量大，因此需要通过改进算法来减小其计算量以便增强算法的实时性。

循环谱密度计算方法为：

直扩信号的循环谱密度函数为：

式中：Q(f)为码元包络q(t)的傅里叶变换，是一个sinc 函数；α是信号s(t)的循环频率。

对高斯白噪声来说，在α≠0 时，其循环谱密度函数(f)=0。这样，可以利用在α≠0 处是否有谱线出现来判断是否存在通信信号。

取f=0 截面的循环谱密度函数(f)|f=0，其表达式如式（6），其最大值出现在α=±f0处，由此可估计出信号载频。

此后，更多学者对循环谱算法进行了更深入的研究。文献[28]提出有限时间平均循环自相关法（Time-variant Finite-average CyclicAutocorrelation，CA）。通过观察谱相关密度函数有无谱线，可以检测信号的有无，并能估计信号载频和伪码速率。而后将该方法与有效抑制噪声的集平均法相结合，进一步提高了检测性能。文献[29]在循环谱法检测法的基础上使用深度残差收缩网络（Deep Residual Shrinkage Network，DRSN），利用机器学习的方式识别信号类型，并结合软阈值判决和注意力机制对抗噪声和干扰，获得了更高的检测精度。文献[30]提出基于分数低阶循环谱（Fractional Lower Order Cyclic Spectrum，FLOCS）的检测算法。文献[31]提出了一种基于循环相关熵谱的AMC 方法，可以有效地抑制脉冲噪声。文献[32]提出结合卷积神经网络去噪模块的循环谱检测方法，可有效对抗噪声，并提出使用二维（2-D）截面方法减少计算数据量，提高了检测效率。文献[29]将3 维循环谱图转换为灰度图像组成数据集，并开发了具有软阈值和注意力机制的DRSN，具有良好的抗噪性能。文献[33]提出了基于广义二阶循环谱的参数估计算法，该算法在alpha 稳定分布噪声中具有良好的检测效果。文献[34]提出结合奇异值分解（Singular Value Decomposition，SVD）降噪的循环谱算法，实现了在弱信号中检测扩频信号的频率分量。

2.2.3 高阶谱检测法

高阶统计量是指阶数大于二阶的统计量。由于任何高斯过程的高阶累积量均等于零，高斯噪声在进行高阶运算后，其值应为0，而直扩信号的信息将会得到增强，然后根据检测接收信号高阶谱线的有无判断是否存在直扩信号。高阶谱检测法的优点：一是可以完全抑制高斯白噪声，二是高阶累积量比二阶累积量具有更丰富的信息。

文献[35]提出采用四阶谱来检测直扩信号，同时估计载频和伪码周期。文献[36]提出了四阶累积量2-D 切片算法，它是高阶累积量的一种简化算法，能够降低计算复杂程度，并且能够取得较好的检测性能。文献[37]提出基于小波分解与延时相乘的四阶累积量改进算法，进一步提高了算法抗噪声性能。

2.3 扩频码周期检测

2.3.1 时域自相关检测法

自相关检测算法利用了信号和噪声在自相关域上的差别来构造检测器，信号在不同时刻间具有关联特性而随机噪声间并无关联。针对直扩信号，该算法利用了伪码良好的自相关特性和周期性。并且，该算法不单单能检测短码直扩信号，对于长码直扩信号也能进行检测。但该算法在低信噪比下的性能并不理想。信号自相关计算方法为：

直扩信号在经过自相关运算后会在整数倍码周期位置上出现尖锐的相关峰，由此可得到码周期估计结果。

此后，Bouder 等人[38]在此基础上，提出进行分段叠加、平滑的思想，并且进行二阶矩计算来改进自相关算法的性能，大大加强了算法的抗噪声性能。张铮提出基于分段集平均和区域能量检测的改进自相关检测方法[39]。孔德阳提出了基于预测的时域相关算法，通过增加数据长度可以提升算法的性能，相比于最原始的时域相关算法，检测不需要扩频码的周期及同步位置，解决了时域相关算法在实际应用中的难点[40]。文献[41]研究了结合时域自相关法和相关函数二阶矩法来改进算法性能的方法，并在此基础上加入改进的自适应噪声抵消器，使得该方法比传统自相关检测算法检测性能更优异，提升了传统检测算法的抗噪声容限，并能有效地实现低信噪比下直接序列扩频信号的检测。李思佳针对低信噪比下传统自相关检测法的自相关峰不易提取，以及相关函数二阶矩算法每段数据点个数不易确定的问题，提出基于小波分解与延时相乘的自相关检测改进算法，使得最终的自相关峰更加清晰，更易于直扩信号的检测[37]。文献[42]提出了基于估计和加权累积的时域滑动相关累积（ETSCA）算法，可在更低信噪比条件下，实现信号检测。文献[43]提出基于适当阈值准则的自相关波动检测法，在密集多信号环境下可有效检测直扩信号。文献[44]提出了一种基于分数低阶自相关的抗脉冲噪声的扩频信号检测算法，具有较好的鲁棒性。

2.3.2 二次功率谱检测法

二次功率谱方法首先对接收信号求取功率谱，其次对求得的功率谱进行一次功率谱求解计算。根据直扩信号的特点，直扩信号的二次功率谱会在扩频码周期的整倍数处出现一系列离散的谱线，由此来估计扩频信号的扩频码周期。扩频码的长度越长，能成功估计出码周期时信号的信噪比容限越低，估计性能越好[45]。该算法的估计性能稳定且时效性较好，同时可以很好地抑制噪声的影响。

二次谱算法计算方法为：

式中：FFT[·]为傅里叶变换；S(f)为信号的功率谱。

文献[46]采用基于分数阶原点矩统计量的最大熵概率密度谱（PDF）估计的方法估计出窄带脉冲干扰的概率密度谱，而后设计滤波函数对信号滤波来抑制窄带脉冲干扰。在此基础上，进行二次谱估计，大大提高了二次谱检测算法的性能，并进一步利用Viterbi 算法提取直扩信号的扩频序列及周期等信息，从而实现对扩频信号的盲解调。文献[47]通过修改分段长度、提取不相邻峰值和重叠分段等方法对二次谱法进行改进，使得算法在低信噪比下实用性更强、估计精度更高。文献[48]研究了二次谱算法对可变扩频长度直扩信号的检测。

2.3.3 倒谱检测法

倒谱法是利用直扩信号扩频码序列的周期性重复和有尖锐的自相关峰的特性，先对直扩信号求取功率谱，然后对其求对数运算，再进行一次求取功率谱计算。直扩信号经过两次功率谱和取对数运算处理后，在谱图上会出现周期的谱峰，并且相邻谱峰间距即为扩频码的码周期。这种算法具有检测效率高、实时性强、结构简单的优点。

倒谱法计算方法的公式为：

倒谱法[49]通过检测单根谱线来判断直扩信号的有无，但在信道环境较差、直扩信号信噪比较低时，特征谱线常常“淹没”于噪声中，难以检测。文献[39]提出通过Welch 法改善功率谱估计，在一定程度上提高了谱检测性能，并通过集平均处理突出低端谱线，再通过检测谱线附近区域平均幅度与整个倒谱域幅度的差值避免检测单根谱线所受干扰，提高了检测稳定性。

2.4 扩频码速率检测

2.4.1 延迟相乘检测法

延迟相乘检测法先将直扩信号与自身经过固定延时的信号相乘，而后再求其功率谱。由于直扩信号在基带上是经过相同的扩频码序列调制过的，所以经过延时相乘后的功率谱表现出了一系列连续的谱线，这些谱线不但能够证明直扩信号的存在，而且可以通过处理，计算出扩频码的码速率。

由于延迟相乘法在噪声功率较大、信噪比较低环境下的信号检测和参数估计效果不是很理想，此后学者对其进行了改进。文献[41]对延迟相乘后的信号进行自相关运算，而后分析信号的频谱，提升了算法检测性能，在噪声功率较大时，也可以检测出谱线，抗噪声能力更强，检测性能更优异。文献[50]提出了基于延迟相乘-相关及谱分析的直扩信号检测法，该方法不仅适应直扩信号检测的低信噪比要求，而且能够更方便地实现对直扩信号符号周期和码片时宽的估计，提高了检测性能。

2.4.2 小波变换检测法

小波变换（Wavelet Transform，WT）是一种时频变换分析方法，它继承和发展了短时傅立叶变换局部化的思想，同时又克服了窗口大小不随频率变化等缺点，能够提供一个随频率改变的“时间-频率”窗口，是进行信号时频分析和处理的理想工具。在扩频信号Haar 小波变换的频谱图中，在码速率为整数倍时会出现峰值，由此，可以通过峰值来检测信号，并可以用来估计信号的码片速率[51]。虽然小波变换方法检测效果较好，但是随着小波基的确定，会造成信号能量的泄露，产生虚假谐波的现象。

另外，小波变换还有一个重要应用就是小波去噪。其原理是通过对含噪信号进行小波分解，对分解得到的小波系数进行某种处理，以去除其中包含的噪声；然后对处理后的小波系数进行重构，进而得到去噪后的信号。多位学者提出了结合小波去噪的扩频信号检测算法，进一步提高了检测性能。杨凯提出了基于小波去噪的延迟相关算法，其性能要优于单纯小波变换检测算法[52]。文献[53]采用小波包能量分解方法去噪，能够对截获的通信信号进行去噪处理，从而提高信号的信噪比，提高检测性能。

2.5 其他检测法

2.5.1 基于卷积神经网络检测法

文献[54]提出一种基于卷积神经网络的直接序列扩频信号检测方法，利用深度学习的方法自动识别扩频信号和噪声的特征，获得了比传统检测统计特征方法更好的检测性能。同时，为降低计算复杂度，提出基于混合卷积神经网络和自相关（Convolutional Neural Network-Correlation，CNNCORR）的检测方法，也能较好地保证算法检测性能。

2.5.2 正交分路副峰等间距检测法

文献[55]针对BOC 调制信号具有的多峰值特点，提出了正交分路副峰等间距检测法，实现了对新形式扩频信号的检测。

2.5.3 分数阶傅里叶变换检测法

文献[56]提出了基于分数阶傅里叶变换（Fractional Fourier Transform，FRFT）的线性调频信号参数快速估计算法。该算法首先对信号进行一次短时傅里叶变换来判断调频斜率的正负，而后利用所提出的高效FRFT 获得初始旋转阶次，最后利用分数阶频谱4 阶原点矩，进一步确定搜索区间和步长，实现对线性调频信号调频率的精准搜索。

3 结语

随着通信技术的不断发展，扩频通信的应用将会越来越广，同时新型扩频信号的提出会导致信号的可检测性能不断降低，迫切需要性能更好的信号检测技术。本文结合国内外信号检测研究现状，总结出了5 种扩频信号检测算法，希望能对同行学者提供一定参考。