基于深度学习的变宽度浓度梯度芯片性能预测

俞俊楠，俞建峰，程洋，齐一搏，化春键，蒋毅

（1 江南大学机械工程学院，江苏 无锡 214122；2 江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122）

由于各个人体间的药物反应、生理状态和遗传特征都存在着一定的差异，个性化医疗对特定个体的精准治疗有着巨大潜力[1]。3D打印作为个性化医疗中极具前途的手段[2]，需要指定的药物混合溶液作为原料。细胞分选[3]、药物筛选[4]和液滴生成[5]等研究则要求药物混合溶液具有指定的浓度和流速。目前主要通过手动移液[6]和移液机器人[7]等方式制备溶液，但是手动移液效率低且精度差，移液机器人造价贵且不易携带。

浓度梯度芯片拥有着溶液制备效率高、样品耗费量少和能够指定出口浓度和流速等特点[8-9]，在化学[10-11]、生物[12-13]和医疗[14-15]等领域得到了广泛的使用。Walker 等[16]在2004 年利用交叉混合微流控装置实现病毒浓度的钟形分布，用于在微尺度环境内进行病毒感染细胞的研究。Saad 等[17]在2019 年提供了一种优化培养藻类的浓度梯度芯片，在200s之内可以生成不同浓度的培养液液滴，节省了制备溶液所需的试剂和时间。关尧[18]在2021 年提出了一种用于生成药物微球的浓度梯度微液滴芯片，实现了浓度可调、粒径可控的药物微球制备。目前，为了得到符合预期性能的浓度梯度芯片，首先需要在三维建模软件中设计具有特定结构的芯片模型，然后制造芯片并通过实验验证性能；如果芯片的性能不符合预期，研究人员就需要重新设计芯片结构，重新制造并验证芯片的性能。设计的芯片结构存在着一定的盲目性，从而导致浓度梯度芯片的设计效率低。

深度学习为建立不同几何结构下的浓度梯度芯片性能预测模型提供了新的途径[19-20]。人工神经网络作为一种可靠的建模和预测工具，常用于解决复杂的实际问题[21]。卷积神经网络通过卷积层、激活函数和池化层理解图像的特征并将其与对应的标签建立联系，以实现图像分类和目标识别任务[22-23]。Wang等[24]在2016年提出了一种随机等宽度（REW）浓度梯度芯片的设计方法，将通过仿真模拟方法得到芯片的几何结构和出口浓度存储在数据库中，用户根据浓度需求在数据库中查询就可以得到对应的芯片结构设计。在此基础上，Ji等[25]在2018年提出了一种基于人工神经网络的REW 浓度梯度芯片自动设计方案，在研究中通过改变部分出口流道的长度来改变浓度梯度芯片的出口浓度，并基于人工神经网络预测模型构建了芯片部分出口流道长度和出口浓度的数据库。为进一步提高浓度梯度芯片的设计效率，Wang 等[26]在2021 年提供了一种基于卷积神经网络的REW浓度梯度芯片流体行为预测方法，采用仿真模拟得到的REW 浓度梯度芯片出口流体行为数据集训练卷积神经网络并建立预测模型。综上所述，目前在REW 浓度梯度芯片的设计研究中仍存在三个方面的不足：①REW 微流道出口浓度和出口流速的分布范围狭窄，出口流速主要集中在4～10mm/s 的范围内，出口A 的浓度主要集中在90%～100%的范围内，出口C 的浓度主要集中在0%～10%的范围内；②一个BP神经网络预测模型只能满足4320 个出口浓度的预测，为了实现更多出口浓度的预测需要建立更多的预测模型，导致预测时间的增加、设计效率的下降；③目前研究中采用的卷积神经网络模型准确率较低，模型预测准确率仅为88%，仍存在提升的空间。

为解决上述三个问题，本研究提出了一种基于深度学习的随机变宽度（RVW）浓度梯度芯片性能预测方法。在单相流网格微流道的基础上，通过不同变宽度微流道的组合来设计RVW 浓度梯度芯片。采用RVW 浓度梯度芯片出口流体行为COMSOL模拟数据训练卷积神经网络并建立预测模型。在3D打印的RVW浓度梯度芯片上验证不同初始入口条件下预测模型的准确性。结果表明，本研究中提出的RVW 浓度梯度芯片拓展了出口浓度和出口流速的分布范围，建立的卷积神经网络预测模型准确率高，可实现RVW 浓度梯度芯片的高效准确设计。

1 浓度梯度芯片流道结构设计

浓度梯度芯片中流道流阻的计算如式(1)所示。

式中，R为流道流阻，Pa·s/m3；μ为流体动力黏度，Pa·s；l为流道长度，m；d为流道宽度，m；h为流道高度，m。

由式(1)可知，通过改变微流道的宽度可以改变浓度梯度芯片的出口浓度和流速。为了改善REW微流道的出口浓度与流速分布，在REW微流道的基础上，通过组合不同变宽度微流道来设计RVW 浓度梯度芯片，两种微流道的结构如图1所示。

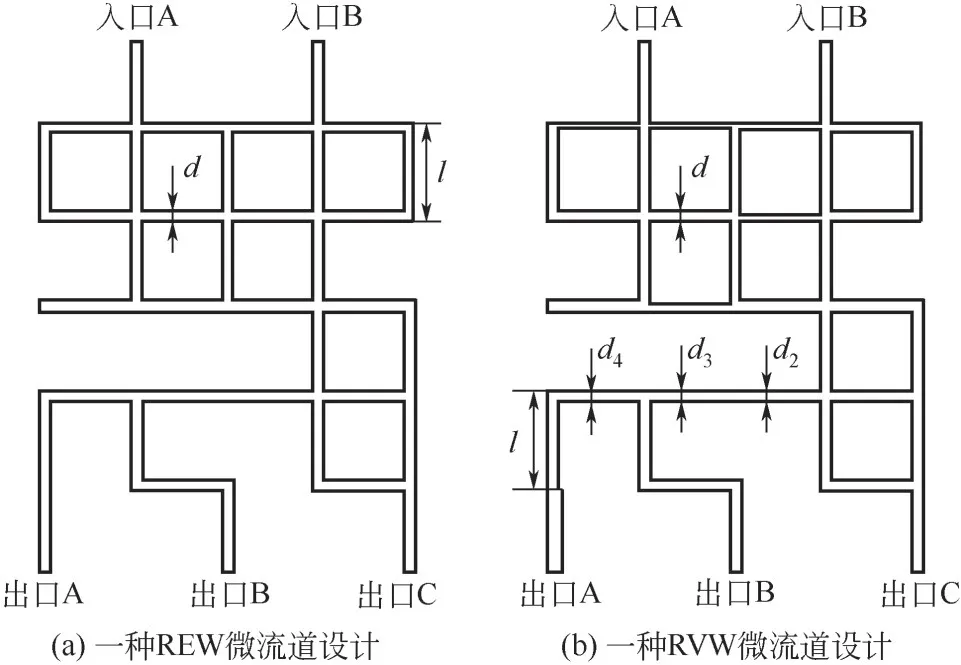
图1 两种微流道结构设计

REW 微流道宽度均为d，在设计中随机出现，有22n2-2n种可能的设计方案，其中一种REW 微流道的结构设计如图1(a)所示。RVW微流道宽度为随机的d、d1、d2和d3，不同宽度的微流道在设计中随机出现，有52n2-2n种可能的设计方案，其中一种RVW 微流道的结构设计如图1(b)所示。在上述的微流道结构设计方案中，微流道高度h为0.05mm；微流道宽度分别有以下4 种情况，即d为0.6mm、d1为0.5mm、d2为0.4mm 和d3为0.3mm；微流道长度l为5.0mm。

2 研究方法

2.1 技术路线图

根据本研究内容，制定了如图2所示的技术路线图。首先，通过不同变宽度微流道的组合，设计了RVW 浓度梯度芯片。其次，通过MATLAB 控制COMSOL 仿真模拟软件对RVW 浓度梯度芯片的出口流体行为进行模拟，随后构建了RVW 浓度梯度芯片出口浓度数据集和RVW 浓度梯度芯片出口流速数据集。再次，提出了KD-MiniVGGNet 模型，采用出口浓度数据集和出口流速数据集分别训练后得到了Concentration NET模型和Velocity NET模型。然后，使用Concentration NET 模型和Velocity NET模型分别预测了测试集中RVW 浓度梯度芯片的出口浓度和出口流速。最后，在3D打印的RVW浓度梯度芯片上验证了不同初始入口条件下的预测模型准确性。

图2 技术路线

2.2 仿真模拟方法与参数设置

通 过COMSOL Multiphysics 5.6 和MATLAB 2020a 联合完成RVW 浓度梯度芯片与REW 浓度梯度芯片的仿真模拟。在本研究的条件下扩散系数影响有限[24]，故将水作为流体材料。模拟条件设置如下，入口A 和出口B 的初始流速均为10mm/s，入口A和入口B的初始浓度分别为1mol/m3和0，在后续的研究中若无明确说明，所述浓度均表示当前溶液浓度占入口A浓度的百分比，表示为百分比浓度但是不指代具体浓度类型。比如，采用百分比浓度表示的入口初始浓度分别为100%和0。流道壁面设定为不可压缩的非滑移界面，模拟参数和边界条件的具体设置见表1。在多物理场耦合中，将层流模块设置为源接口，稀物质传递模块设置为目标接口。在每完成1 个浓度梯度芯片的仿真模拟之后，通过MATLAB 2020a 将模拟得到的出口浓度矩阵、出口流速矩阵和几何模型文件存储在MySQL 数据库中。模拟得到的出口浓度矩阵、出口流速矩阵和几何模型文件将用于后续的仿真模拟结果讨论和卷积神经网络训练。

表1 模拟参数和边界条件设置

2.3 浓度梯度芯片的数学表达

为了加速卷积神经网络的训练，采用如图3所示的几何特征矩阵表示微流道的几何结构作为神经网络的输入。其中，数字1 代表微流道的交叉结点，数字d、d1、d2和d3分别代表微流道的不同宽度，数字0表示此处没有微流道出现。

图3 几何特征矩阵

2.4 模型搭建

2.4.1 KD-MiniVGGNet模型

作为预测模型输入的几何特征矩阵大小为9×9，为了保证卷积运算的连续性，首先尝试了如表2 所示的MiniVGGNet[27]模型。然而，该模型只有4个卷积层，模型非线性变化不足，特征表达能力差，导致了预测准确率相对较低。因此，本研究基于卷积核分解原理在MiniVGGNet 的基础上构建了KD-MiniVGGNet模型。

表2 MiniVGGNet模型主要结构

KD-MiniVGGNet模型的主要结构见表3。主要有以下特点：①在卷积层中使用32 和64 的通道数，限制了模型参数量以及模型计算复杂度；②将通道数不变化的卷积层分解为2 个使用2×2 卷积核[28]的叠加卷积层，增加了模型的深度；③在模型的阶段一中连续使用8个卷积层Conv2～Conv9，在阶段二中使用2个卷积层Conv11～Conv12，且均采用2×2卷积核，保证了模型的非线性变化能力与特征表达能力。此外为了保证分解效果，Conv1 与Conv10两个通道数发生变化的卷积层均保持3×3卷积核。模型共有14 个权重层，激活函数均采用ReLU激活函数。

表3 KD-MiniVGGNet模型主要结构

2.4.2 模型性能表征

基于KD-MiniVGGNet 构建ConcentrationNET（出口浓度）与VelocityNET（出口流速）。上述模型的输入均为9×9的几何特征矩阵，但是Velocity NET的输出为[V'outA，V'outB，V'outC]，Concentration NET的输出为[C'outA，C'outB]。由于Concentration NET 在实际训练时难以适应出口C中的浓度分布，所以出口C的浓度采用如式(2)所示的质量守恒定律计算。

式(2)中，VinA和VinB为入口A 和B 的初始流速，mm/s；CinA和CinB为入口的初始浓度，%；V'outA、V'outB、V'outC为出口A、B 和C 的流速预测值，mm/s；C'outA、C'outB和C'outC为 出 口A、B 和C 的 浓 度 预 测值，%。

在训练过程中，使用均方误差（MSE）计算ConcentrationNET 与VelocityNET 的损失。损失函数值越小，表示神经网络模型预测值和目标值之间的差异越小，神经网络模型的性能越好。准确率计算如式(3)和式(4)，准确率越接近于100%，表示模型性能越好。

式中，k为芯片序号；n为芯片数量；；CoutA,k和CoutB,k分别为出口A 和B 的浓度目标值，%；VoutA,k、VoutB,k和VoutC,k为出口A、B和C的流速目标值，mm/s；ΔCoutA,k和ΔCoutB,k分别为出口A 和B 的浓度预测值和浓度目标值之间的差值，%；ΔVoutA,k、ΔVoutB,k和ΔVoutC,k分别为出口A、B和C的流速预测值和流速目标值之间的差值，mm/s。

2.4.3 卷积神经网络的求解过程

前向传播算法，具体是指将上一层神经元的输出作为下一层神经元的输入，然后计算得到下一层神经元的输出，直到完成最后一层输出层的计算。反向传播算法，具体是指将通过损失函数计算得到的误差反向传递到输入层，在此期间通过对权重参数和偏置项的不断迭代更新来提高模型的准确性。模型的训练和应用共同组成了卷积神经网络模型的求解过程，具体步骤如图4所示。从图中可知，模型的训练由前向传播算法和反向传播算法实现。模型的应用过程则是通过训练好的模型，由前向传播算法输出结果。

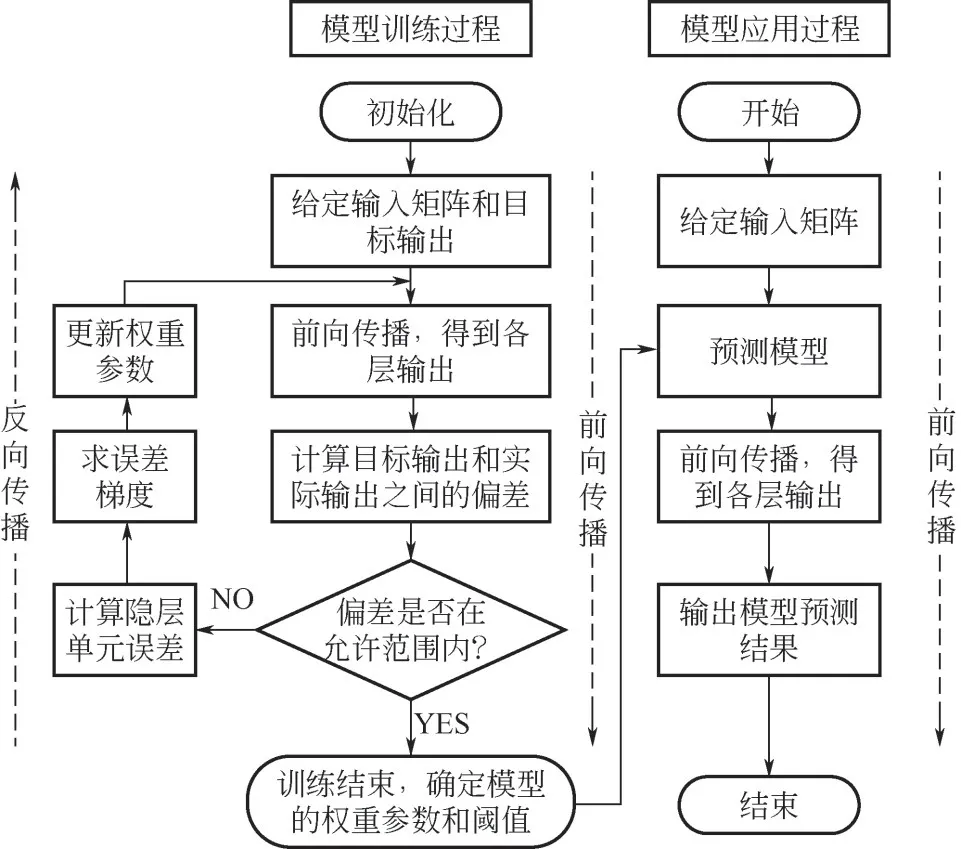
图4 卷积神经网络的求解过程

模型的具体训练过程如下：

（1）假设输入样本数量为m，最大迭代次数S，当前的隐层序号为l，随机初始化模型中的权重参数w和偏置项b。

（2）迭代开始，迭代步数s从1至S。

①输入样本为ai,1，样本序号i从1至m。

②前向传播计算。

对于隐藏层，式(5)～式(7)分别对应卷积层、池化层和全连接层中前向传播的计算过程。此时l范围为2～(L-1)。

③对于输出层，前向传播的计算过程如式(8)所示。

④通过损失函数计算得到输出层的误差δi,L。

⑤反向传播计算。

对于隐藏层，式(9)～式(11)分别对应全连接层、卷积层和池化层中反向传播的计算过程。此时l范围为(L-1)～2。

⑥权重参数w和偏置项b的更新只发生在全连接层和卷积层中，此时l的范围为2～L。

当第l层为全连接层时，更新方式如式(12)和式(13)所示。

当第l层为卷积层时，更新方式如式(14)和式(15)所示。

⑦当权重参数和偏置项的变化值小于停止迭代阈值ε时，固定权重参数w和偏置项b。

（3）迭代结束，得到预测模型。

2.4.4 训练策略

将浓度梯度芯片的几何特征矩阵作为模型输入，出口浓度矩阵与出口流速矩阵作为模型输出，构建出口浓度数据集与出口流速数据集。按9∶3∶4的比例将上述数据集分别分割出训练集、验证集和测试集，并且三者中均不存在重复数据。每个训练轮次之后，在验证集上验证模型性能，得到当前权重参数下的损失，并与前一个训练轮次中得到的损失进行比较，保存损失较小的模型权重参数，以便在收敛后获得最佳的预测模型。ConcentrationNET和VelocityNET 通过PyTorch 在Python 3.8 中实现，并在一台搭载着AMD Ryzen 5 4800h CPU 芯片、16GB 运行内存和NVIDIA GTX 1650 GPU 的计算机上进行训练和测试。

2.5 实验材料和方法

2.5.1 试剂与设备

实验所用试剂见表4。在本次实验中采用亚甲基蓝溶液作为入口物料，浓度可以通过分光光度法来进行检测。实验所用试剂中，亚甲基蓝为标准溶液，质量浓度为1mg/mL；双氧水的质量分数为30%。实验所用设备见表5，包括设备型号及生产厂商。

表4 实验所用试剂

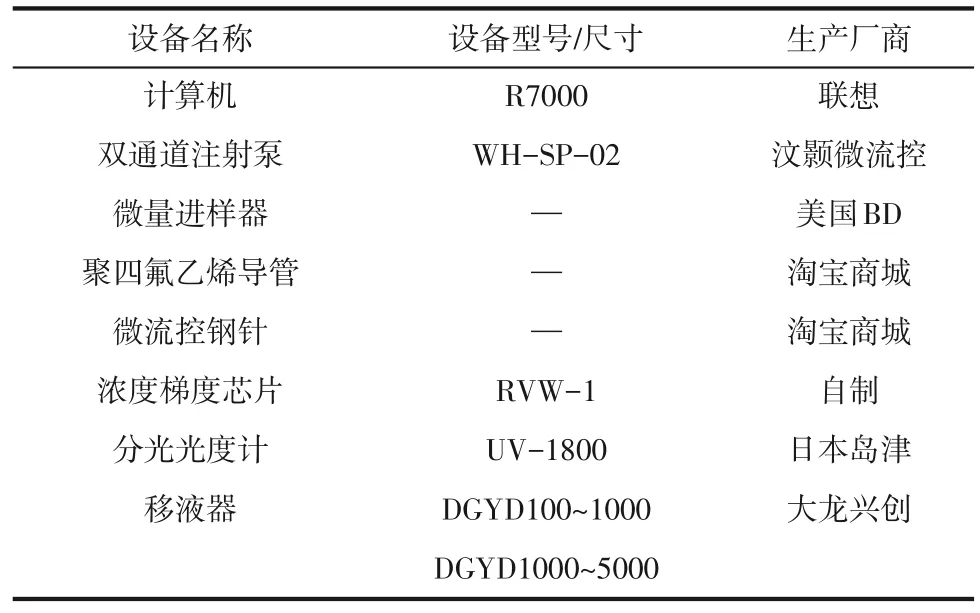
表5 实验所用设备

2.5.2 浓度梯度芯片验证实验研究系统组建

首先在RVW 浓度梯度芯片出口流体行为的测试集中随机挑选一个微流道；然后将在COMSOL Multiphysics 5.6 中建立的几何模型导入SolidWorks 2021 中完成修改，浓度梯度芯片的模型结构如图5(a)所示，主要由进料区A、浓度梯度生成区B 和出料区C 三个区域组成；最后通过3D 打印得到如图5(b)所示的浓度梯度芯片样品。将浓硫酸和质量分数为30%的双氧水以7∶3 的体积比混合，配置食人鱼溶液用于去除微流道内部杂质并提高表面亲水性。

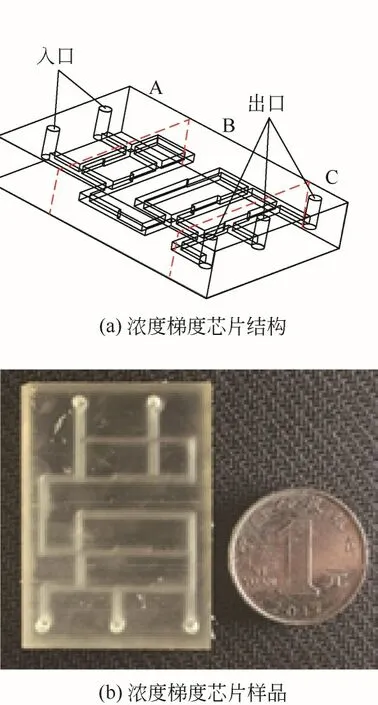
图5 浓度梯度芯片结构及样品

如图6 所示，实验系统主要由双通道注射泵、浓度梯度芯片、集液瓶、分光光度计和电脑组成。首先，将直径为2.0mm的微流控钢针通过热熔胶安装在浓度梯度芯片的入口和出口处；其次，通过内径为1.8mm的聚四氟乙烯导管将微量进样器和浓度梯度芯片入口处的微流控钢针连接；然后，将内径为1.8mm的聚四氟乙烯导管通过热熔胶固定在出口的微流控钢针处，聚四氟乙烯导管的出口与集液瓶相连；最后，通过分光光度计检测集液瓶中溶液的吸光度。连接处的热熔胶都起到了固定和密封的作用。

图6 实验系统

2.5.3 实验方法

讲练结合法是讲授法和练习法相结合的方法。教师边讲，学生边练既可以活跃学习气氛，又能够及时发现问题和解决问题。电工基础课具有课程内容比较多，公式比较多，习题量比较大，课时比较紧张，解题技巧比较灵活的特点，在教学中发现，学生在教师讲授时听懂了，可是自己做练习时却无从下手或出现错误比较多的现象。例如在讲授支路电流法这一节课的内容时，学生似乎掌握了列写回路电压方程和节点电流方程，但在实际练习过程中会出现各种各样的问题：不能正确标注回路的绕行方向，回路中各电阻元件的电压参考方向不能正确标识，回路中各电阻元件电压的正负号把握不准等等。所以在教学过程中，采用讲练结合法时非常有必要的。

分别在不同入口流速和不同入口浓度两种初始条件下验证预测模型的准确性，通过迁移学习得到不同初始入口条件下的模型预测值。

（1）取1mg/mL 亚甲基蓝标准溶液1mL 定容至50mL，得到20μg/mL的亚甲基蓝溶液。

（2）保持其他入口条件一致，改变入口溶液的流速。使用两个微量进样器分别吸取去离子水和20μg/mL 的亚甲基蓝溶液各10mL，改变浓度梯度芯 片 的 入 口 流 速（10mm/s、15mm/s、20mm/s、25mm/s和30mm/s），使用分光光度计分别对得到的出口溶液样品进行检测，在同一条件下重复实验5次。

（3）保持其他入口条件一致，改变入口溶液的质量浓度。使用两个微量进样器分别吸取去离子水和5μg/mL、7μg/mL、10μg/mL、15μg/mL、17μg/mL、20μg/mL 的亚甲基蓝溶液各10mL，浓度梯度芯片的入口流速设定为10mm/s，使用分光光度计分别对得到的出口溶液样品进行检测，在同一条件下重复实验5次。

2.5.4 分析方法

亚甲基蓝溶液的浓度通过分光光度法确定。配置0、5μg/mL、7μg/mL、10μg/mL、15μg/mL、17μg/mL、20μg/mL 的亚甲基蓝溶液，在吸收波长为664nm处检测吸光度，并绘制如图7所示的标准曲线。预测结果与实验结果的绝对误差可由式(16)计算得到。

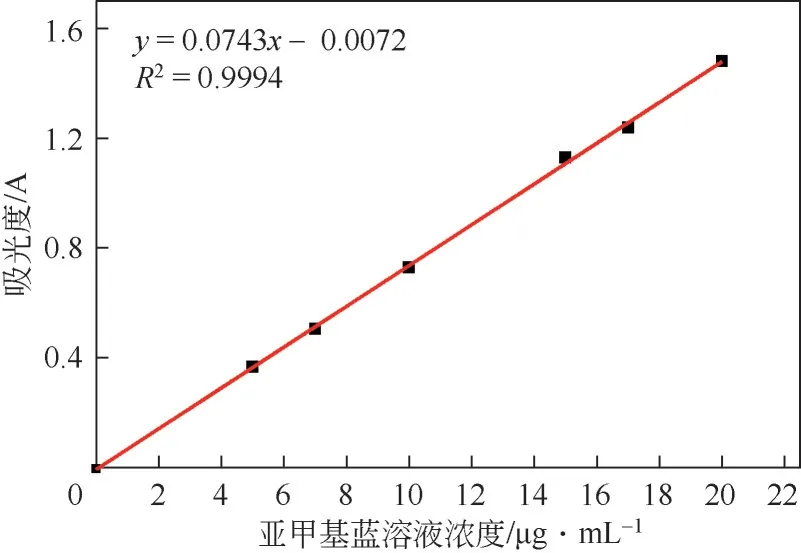
图7 亚甲基蓝溶液标准曲线

式中，n取A、B和C，分别代表出口A、出口B和出口C；C'n为模型预测结果，%；Cn,E为实验结果，%；E为绝对误差，%。

3 结果与讨论

3.1 仿真模拟结果

通过2.2节中仿真模拟方法分别得到包含2000个样本的REW 浓度梯度芯片出口流体行为数据集和RVW 浓度梯度芯片数据集，将模拟结果绘制成出口浓度-出口流速分布图，结果如图8(a)、(b)所示。

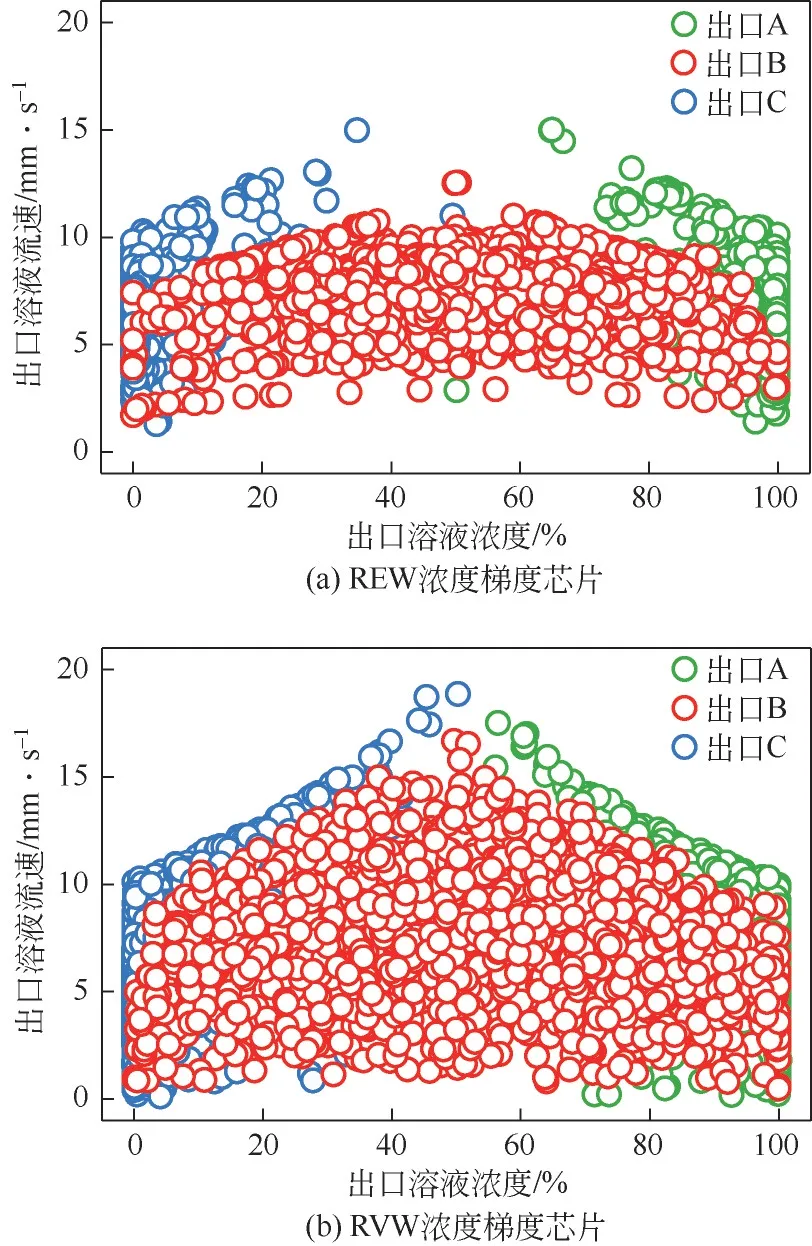
图8 出口浓度-出口流速分布

如图8 所示，REW 浓度梯度芯片的出口流速主要集中于4～10mm/s 之间，其中出口A、B 和C的具体流速范围为1.4～15.0mm/s、1.7～2.5mm/s和1.2～15.0mm/s；RVW 浓度梯度芯片的出口流速主要集中于2～12mm/s 之间，其中出口A、B 和C 的具体流速范围拓展到了0.2～18.9mm/s、0.4～16.8mm/s 和0.2～17.5mm/s。在REW 浓度梯度芯片中，超过90%的出口A、B和C的流速分别位于4～9mm/s、5～10mm/s 和4～10mm/s 之间。在RVW 浓度梯度芯片中，对于同样的流速范围，比例分别为61%、62%和70%，远小于90%，说明RVW 浓度梯度芯片有效地拓展并改善了出口的流速分布。

从图8 可知，REW 浓度梯度芯片中出口A、B和C 的浓度范围分别为50%～100%、0～100%和0～50%；RVW 浓度梯度芯片中的出口浓度范围没有明显改变。这主要是因为出口位置的分布，出口A 靠近高浓度的入口，总能得到较高的浓度输出；出口C则靠近低浓度的入口，总能得到较低的浓度输出；出口B位于入口A和入口B之间，总能提供最广泛的浓度输出。在REW 浓度梯度芯片中，98%出口A的浓度大于90%，90%的出口B浓度位于20%～80%之间，98%出口C 的浓度小于10%。在RVW 浓度梯度芯片中，上述比例分别为89%、74%和87%，可见RVW 浓度梯度芯片有效且显著地改善了出口的浓度分布。

可以看出通过改变流道的宽度确实可以改善浓度梯度芯片出口的浓度和流速分布。这主要是因为随机改变微流道的宽度可以增加流道流阻的组合方式，而浓度梯度芯片中的流道流阻直接影响着着出口浓度和出口流速，所以RVW 浓度梯度芯片可以有效拓展出口浓度与流速的覆盖范围，改善出口浓度和出口流速的分布。

3.2 RVW浓度梯度芯片数据集的建立

本研究中使用MATLAB 2020a 控制COMSOL Multiphysics 5.6 完成所有RVW 浓度梯度芯片出口流体行为的模拟，共花费174h 生成13730 个RVW浓度梯度芯片。在训练中采用几何特征矩阵表示微流道的几何结构作为预测模型的输入，出口浓度矩阵和出口流速矩阵作为预测模型的输出，并与几何特征矩阵一一对应，分别构建RVW 浓度梯度芯片的出口浓度数据集与出口速度数据集。数据集中包括13730个RVW浓度梯度芯片样本，共计41190个出口浓度和出口流速。按2.4.4 节中所述的方法划分上述数据集，训练集中包含有7722 个芯片，验证集中包含有2575 个芯片，测试集中包含3433 个芯片。

3.3 卷积神经网络训练结果

使用RVW 浓度梯度芯片出口流速数据集训练VelocityNET 模 型，其 输 出 为[V'outA，V'outB，V'outC]。批尺寸取16，学习率设为0.0014，采用Adam 优化器训练模型。在200 个训练轮次后，结果如图9(a)所示。VelocityNET 在验证集上的预测准确率为93.5%，损失为2.1×10-7。在测试集上进行测试，获得模型准确率为92.7%。图9(b)显示了测试集中模型预测结果与目标结果之间的绝对误差，其中出口A、B 和C 中分别有95.8%、97.7%和95.3%的出口流速绝对误差小于1mm/s；当出口流速的绝对误差为2mm/s，三个出口中分别有99.5%、99.9%和99.7%的出口流速满足误差要求；当设定的绝对误差为3mm/s时，三个出口的出口流速满足绝对误差要求的比例分别达到了99.9%、100.0%和99.9%。说明VelocityNET 的预测结果与目标结果呈现出了高度的一致性。

图9 VelocityNET训练结果

使用RVW 浓度梯度芯片出口浓度数据集训练ConcentrationNET 模型，其输出为[C'outA，C'outB]，出口C 的浓度采用质量守恒定律计算。批尺寸取32，学习率设为0.002，采用Adam优化器训练模型。如图10(a)所示，为250个训练轮次后的得到的训练结果。ConcentrationNET 在验证集上的预测准确率为92.71%，损失为2.4×10-3。在测试集上进行测试，获得模型准确率为91.5%。图10(b)显示了测试集中所有芯片浓度预测值与浓度目标值的绝对误差，在出口A中有86.9%的出口浓度的绝对误差小于5%，与出口C 的85.9%基本持平，显著高于出口B 的69.9%；当绝对误差为10%时，3 个出口中分别有98.6%、91.8%和98.5%的出口浓度满足误差要求；当出口浓度的绝对误差来到15%时，这个比例分别到达了99.8%、97.2%和99.2%。ConcentrationNET的预测性能略低于VeolocityNET，但仍能取得令人满意的结果。

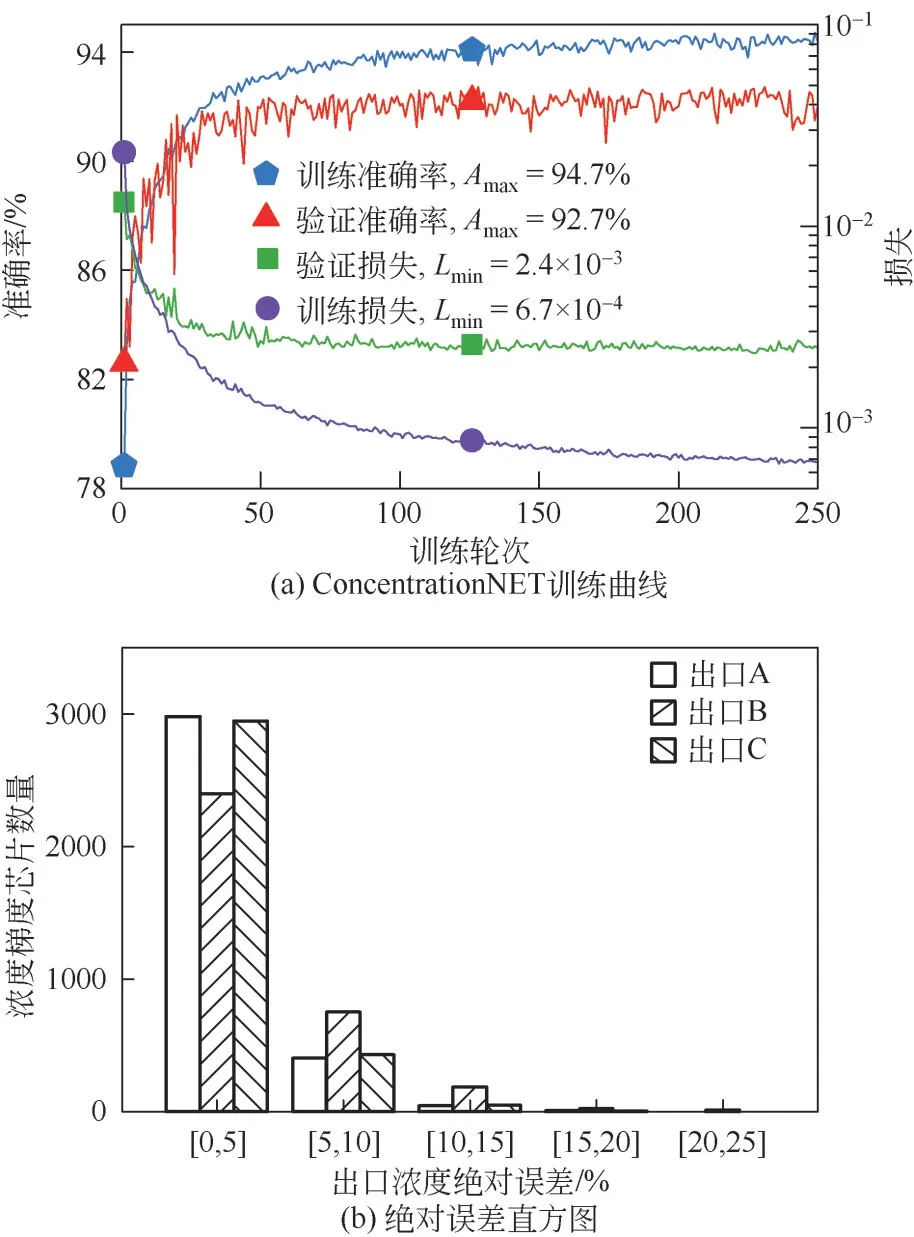
图10 ConcentrationNET训练结果

3.4 不同的初始入口条件下，模型准确性验证

为考察ConcentrationNET 模型在不同入口流速条件下的预测性能，将入口流速为10mm/s、15mm/s、20mm/s、25mm/s和30mm/s范围内的模型预测结果与实验结果进行对比。如图11 所示，随着入口流速的增加，预测结果与实验结果呈现出相同的变化趋势；出口A的出口浓度呈现出缓慢下降的趋势；出口B 的出口浓度呈现出缓慢上升的趋势；出口C 的出口浓度同样呈现出缓慢上升的趋势。这主要是是因为溶液流速的影响了微流道内的传质效率，所以模拟结果和预测结果的出口浓度都呈现出相对一致的变化。将出口浓度换算成入口浓度的百分比，得到每个出口处预测结果与实验结果的平均绝对误差为出口A 的3.4%、出口B 的4.1%以及出口C 的3.0%；最大绝对误差为5.5%，最小绝对误差为2.4%；在不同的入口流速下，综合所有出口的平均绝对误差为3.5%。

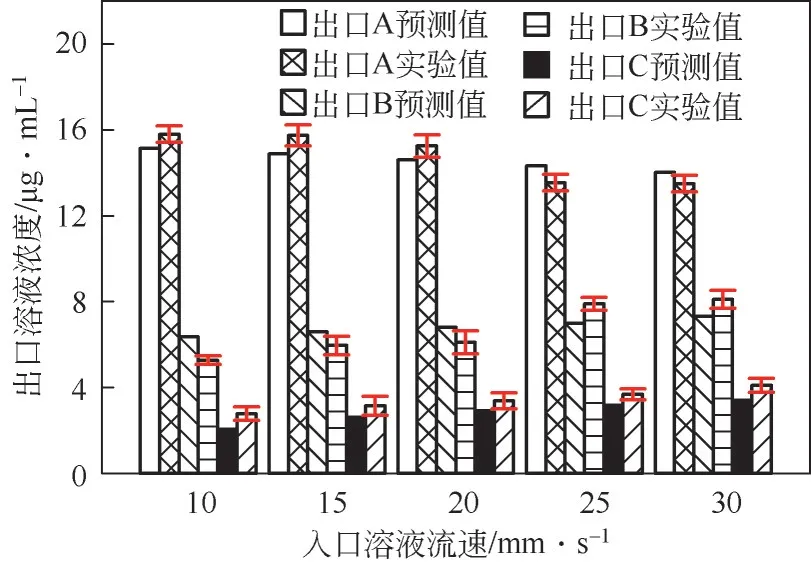
图11 不同入口流速条件下预测结果与实验结果的对比

为考察CconcentrationNET模型在不同入口浓度条件下的预测性能，将入口浓度为5μg/mL、7μg/mL、10μg/mL、15μg/mL、17μg/mL 和20μg/mL范围内的预测结果与实验结果进行对比。如图12所示，预测结果中出口浓度占入口浓度的百分比没有出现显著变化，出口A 的浓度为75.7%，出口B的浓度为31.8%，出口C 的浓度为10.2%。将出口浓度换算成入口浓度的百分比，将模型预测结果与实验结果进行了对比。得到当入口浓度为10～20μg/mL时，出口A的平均绝对误差为4.5%；出口B的平均绝对误差为4.2%；出口C的平均绝对误差为3.8%；最大绝对误差为5.5%，最小绝对误差为3.3%。当入口浓度为5～7μg/mL时，预测结果与实验结果之间呈现出了较大的差距。出口A的平均绝对误差为6.0%；出口B 的平均绝对误差为5.9%；出口C 的平均绝对误差为9.6%。这可能是因为出口浓度过低从而导致实验测量结果出现了较大的偏差，最后造成预测结果和实验结果之间出现了相对较大的差距。在不同的入口浓度下，综合所有出口的平均绝对误差为5.2%。

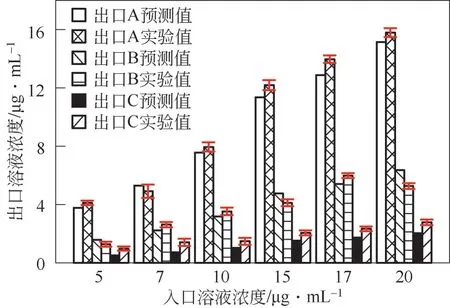
图12 不同入口浓度条件下预测结果与实验结果的对比

4 结论

（1）通过RVW 浓度梯度芯片结构的创新设计实现了出口浓度和出口流速范围的拓展。相较于REW浓度梯度芯片，RVW浓度梯度芯片的三个出口流速分布范围分别拓宽了29%、28%和30%；三个出口浓度分布范围分别拓宽了9%、16%和11%。

（2）基于KD-MiniVGGNet 建立的VelocityNET模型和ConcentrationNET 模型可分别实现对RVW浓度梯度芯片出口流速和出口浓度的精准预测。VelocityNET 模型在出口流速测试集上的预测准确率为92.7%，三个出口中分别有99.5%、99.9%和99.7% 的出口流速的绝对误差小于2mm/s；ConcentrationNET 模型在出口浓度测试集上的预测准确率为91.5%，三个出口中分别有98.6%、91.8%和98.5%的出口浓度的绝对误差小于10%。相较于BP 神经网络预测模型，通过VelocityNET 模型和ConcentrationNET 模型能分别实现41190 个出口流速和出口浓度的预测，显著提高了设计效率。

（3）通过实验在3D打印的RVW浓度梯度芯片上验证了出口浓度预测模型的准确性。当入口流速不同时，浓度梯度芯片出口浓度的平均绝对误差为3.5%；当入口浓度不同时，浓度梯度芯片出口浓度的平均绝对误差为5.2%。