基于LASSO 算法的波束空间信道估计

张珍凤,张文芳

(山西能源学院 电气与控制工程系,山西 太原 030006)

0 引言

在5G 及以上频段毫米波(mmWave)大规模的移动通信中,多输入多输出(MIMO)是其中的关键技术之一[1]。 为了降低大量天线的硬件成本和相关射频链所带来的功耗,透镜天线阵列作为一种高效节能的混合预编码在毫米波大规模MIMO 技术中得到广泛应用[2-3]。 因为透镜天线阵列可以用不同加权系数的天线实现发射或接收空间不同方向的信号。 透镜天线阵列线由于具有空间波束赋形能力,它可以将空间信道转换为波束空间信道,对信号进行空域滤波[4]。 由于在毫米波频率下,只有少数具有较大路径增益的主导传播路径,因此,毫米波大规模MIMO 系统的波束空间信道中很多值为零,只有部分值不为零,所以波束空间信道是稀疏的[5]。 因此,通过选择增益较大的主要波束连接到数字基带的射频链(Radio Frequency,RF),可以使频链数量大大减少。由于信道维度高,而且波束选择需要波束空间中准确的信道状态信息(Channel State Information,CSI)[6],特别是当射频链的数量远远小于天线的数量时[7],如何获得波束空间信道是一个非常具有挑战性的问题。

1 系统模型建立

1.1 空间波束信道

基于毫米波的时分双工(Time Division Duplex,TDD)系统如图1 所示。 基站(Base Station,BS)是一个由N 根天线和NRF条射频链路组成的透镜天线阵列,此透镜天线阵列为K 个单天线用户服务。

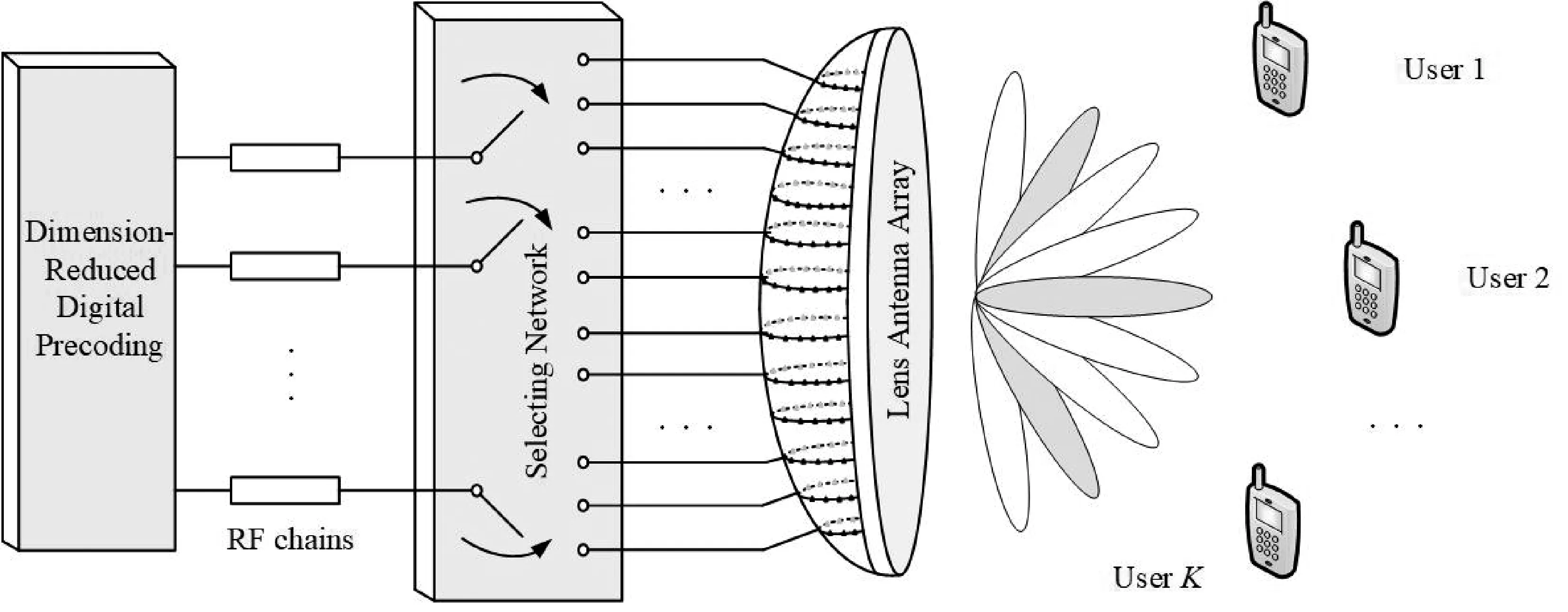
图1 透镜天线阵列多波束空间发射系统

为得到波束信道估计问题,首先,在传统的毫米波MIMO 信道中,根据广泛使用的Saleh-Valenzuela信道模型[8],在第k 个用户和M 根天线的基站之间大小为M×1 信道矢量hk表示为:

其中, Lk是可分辨的信道路径数,ck,l=是第l 条路径,其中,分别是第l 条路径的水平角、俯仰角和复增益。是一个M × 1 维的阵列导向矢量,它和阵列几何结构有关。 对于均匀线性阵列(Uniform Linear Arrays,ULAs),阵列导向矢量与一个角度有关,表示如下[10]:

其中,m = [0,1,…,(M - 1)]T。 空间域信道使用透镜天线阵列转换成波束信道。 透镜阵列相当于空间离散傅里叶变换矩阵F 大小为M × M。 对于ULAs,矩阵F 表示为:

1.2 波速信道估计问题形成

为了获得信道状态信息(CSI),通过Q 个时隙,所有用户把已知的导频符号发送给基站(BS)。 由于TDD 信道的互易性,只考虑上行链路来获得信道估计。 然后,根据估计的上行通道直接得到下行通道。本文采用了广泛使用的正交导频传输策略,其中由于导频的正交性,每个用户的上行信道估计是独立的。 因此可以逐个估计所有K 个用户和BS 之间的波束空间信道向量。 一般情况下,以第k 个用户和BS 之间的波束空间信道向量为例来描述信道估计问题。

在导频传输的第q 时刻,基站侧基带经过波束选择后,NRF×1 维的测试信号yk,q表示为[9]

其中,Ak,q是NRF× M 波束选择网络,sk,q是传送的导频信号,是有效的噪声向量,其中是M × 1 噪声向量,其中为噪声功率。

在经过Q 时刻的导频传输后,假定sk,q=1,q=1,2,…,Q,可以得到N×1(N=QNRF)维的测试信号yk为

由于导频的正交性,所以信道估计算法对于K 个用户是相同的,问题可以进行简化,表示为:

由于l0-范数的非凸性,上式中的问题为NPhard[10]。 因此,通常用l1范数代替l0范数[11],将该问题转化为凸优化问题。 目前已有一些传统的贪心算法, 如有正交匹配追踪(Orthogonal Matching Pursuit,OMP)[8]算法,它可以从带噪测量信号中获得稀疏的空间波束信道信息,还有基于压OMP 改进的缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)[11]算法等都可以实现稀疏信号恢复。 但是,这些贪心算法不能达到令人满意的估计精度。 特别是随着稀疏度的增加,这些贪心算法的计算复杂度也会增加。

2 LARS 算法和改进LASSO 算法

2.1 LARS 算法

最小绝对收缩和选择算子(LASSO)问题描述的是一类有约束的优化问题[12]。 具体定义如下:

其中,X=[x1,…,xm]∈Rn×m是自变量矩阵,y =[y1,…,yn] ∈Rn×1是因变量,取常数。 用xi∈Rn对yi∈Rn进行线性回归,并且回归系数β 的l1范数不超过ε 值。 LASSO 问题是在回归系数β 的l1范数满足一定约束条件下的线性回归问题。 目前,在压缩采样(Compressive Sampling,CS)技术中大多采用LASSO 问题的方式描述。

对于线性压缩采样信号恢复问题,可以用下面的方程描述:

其中,Φ∈Rn×m,n ≪m 为采样矩阵。 y ∈Rn为经过压缩采样后得到的数据。 为了获得原始被测信号x ∈Rm需要求解下面一个优化问题:

或存在误差时

在近似求解方程(11)的所有解中,当x 的l1范数最小时,得到的就是最优稀疏解。 由上可知,LASSO问题中回归系数β 的最优解问题就是稀疏信号恢复优化问题的最优x 求解。 由于波束信道估计问题本质上是一个稀疏信号恢复的问题。 因此,通常在波束信道估计中,把l0- 范数非凸优化问题转化为l1- 范数凸优化问题后,波速信道估计优化问题的求解就和信号恢复优化问题对应,只要把原始被测信号x 换做h,采样矩阵Φ 换做感知矩阵A。 那么就可以使用求解LASSO 问题的方法进行波束信道估计。

最小角回归(Least Angle Regression, LARS)算法能够高效地求解LASSO 问题。 LARS 算法利用高维向量的“角分线”,先找到与因变量相关度最大的自变量,并用其对因变量逼近。 多次逼近直到残差足够小或已取得了所有自变量,算法结束。 下面将介绍LARS 算法解决LASSO 问题(波束信道估计)的具体过程[12]。

在前向逐步回归算法中,它按顺序构建子空间,每次向子空间添加一个变量。 在每一步中,它都确定要在活动集中添加最佳变量,然后更新最小二乘拟合以包含所有活动变量。 LARS 采用相似的策略。 首先,它确定与测量值最相关的活动变量。 LAR 不是完全拟合该活动变量,而是将该活动变量的回归系数连续地沿其最小二乘值方向移动。 在移动的过程中,其与残差的相关性减弱。 当有新的自变量在与残差的相关性“相同”时,这个过程就会停止。 然后,将第二个新自变量加入活动集,将它们构成的回归系数移动到一起,使它们的相关性保持紧密和残差的相关性递减。 这一过程一直持续到所有自变量都在子空间中,并在完全最小二乘拟合时结束。 具体如算法1 所示。

在第k 步开始时,设Jk为活动变量集,hAk为系数变量;将会有k - 1 个非零值,并且刚刚输入的值将为零。 如果当前的残差为rk=y - AJkhJk,则这一步的方向为:

则预测参数将变为hJk(α)=hJk+αδk。 如果这一步开始时的拟合向量是,那么它就演变为+ α·uk,其中,uk=AJkδk是新的拟合方向。 “最小角”这个名字来源于对这个过程的几何解释;uk与Jk中的每个预测值形成最小(且相等)的角度。

算法 1:最小二乘回归(LARS)

(1)将自变量因子A 标准化,使之具有零均值和单位范数。 以残差开始。

(2)找到与r 最相关的自变量aj。

(3)将hj从0 移向其最小二乘系数〈aj,r〉,直到其他自变量ak与当前残差的相关性与aj相同。

(4)沿着〈aj,ak〉 上当前残差的联合最小二乘系数定义的方向移动hj和hk,直到其他自变量al与当前残差有相同的相关性。

(5)按照这种方式继续下去,直到输入了所有k个自变量。 经过min(N - 1,k) 步,得到完整的最小二乘解。

2.2 改进LARS 算法求解LASSO 问题

LAR(LASSO)算法是一种高效的算法,因为它与使用k 个自变量的单个最小二乘拟合具有相同的计算顺序。 最小角度回归总是需要k 步才能得到完整的最小二乘估计。 虽然两种算法有相似之处,但LASSO 算法需要经过多于k 步才能得到最小二乘估计的解。 为此对算法1 进行修正得到算法2。 算法2是计算任何LASSO 问题解的一种有效方法,特别是当k 远远大于N 的时候。 Osborne 等[12]还发现了计算LASSO 问题的分段线性路径,称之为同伦算法。

算法2:最小二乘回归(LARS)——改进LASSO如果非零参数达到零,则将其自变量从活动变量集中删除,并重新计算当前联合最小二乘方向。

2.3 近似消息传递算法

迭代近似消息传递(Approximate Message Passing,AMP)算法收敛速度快,可以恢复计算复杂度低的稀疏信号,特别是对高维稀疏信号。 在本小节中,将介绍AMP 算法如何估计波束空间信道,如算法3 所示。

在算法3 中,步骤1 中的项btvt-1和被称为Onsager 修正,它们被引入AMP 算法以加速收敛。AMP 算法的关键步骤是步骤4,通过软阈值收缩函数ηst获得第t 次迭代中估计的。 收缩函数ηst是非线性元素运算,它考虑了矢量的稀疏性,使得的估计值更稀疏。 对于第i 个元素rt,i=| rt,i| ejwt,i(i=1,2,…,N) 的输入向量rt,有

其中,wt,i为复值元素rt,i的相位,λt为第t 次迭代中预先确定的固定参数,通过估计步骤2 中的噪声方差来更新。 由(15) 可以发现,软阈值收缩函数ηst可以将低功率复值输入的幅值缩小到零。 在步骤5 和步骤6 中,分别计算了收缩函数ηst在输入向量r 及其共轭向量r∗处的逐元素导数,得到bt+1和ct+1。 AMP 算法能很好地处理大规模稀疏信号恢复问题。

算法3:近似消息传递(AMP)

输入:测量矩阵y,感应矩阵A,迭代数目T

初始化:v-1= 0,b0= 0,c0= 0,

for t = 0,1,…,T - 1 do

end for

3 实验仿真

在仿真实验中,笔者认为BS 有M=256 个透镜天线阵列和NRF=16 个射频链。 单天线用户数设置为K=16。 测量次数设置为N=128。 上行信道估计的信噪比定义为1/σ2m。 然后,根据Saleh-Valenzuela 信道模型生成空间信道样本。 对于(1) 中的Saleh-Valenzuela 信道模型,路径数为Lk= 3,βk,l~ CN(0,1),,l =1,2,3。 笔者为每个用户k设置相同的信道参数验证LARS 算法和改进LASSO算法。 最后,利用归一化均方误差(NMSE) 评价LARS 算法的性能。

为了找出训练阶段的最佳信噪比设置,笔者对不同信噪比下算法的NMSE 性能进行了比较,如图2 所示。 在 本 小 节 中, 笔 者 考 虑 了 ULA 的 Saleh -Valenzuela 通道模型,并提供了OMP 算法、改进LASSO 算法和LARS 算法的波束空间信道估计性能比较。 图2 中为在不同信噪比下上述3 种算法的NMSE 性能比较。 如图2 所示,随着信噪比增加,波束空间信道估计精度逐渐提高。 同时,从图1 可以得出与传统的OMP 算法相比,所提出的改进LASSO 算法和LARS 算法在所有考虑的信噪比区域都具有更低的估计误差,改进LASSO 算法比LARS 算法具有更好的NMSE 性能。

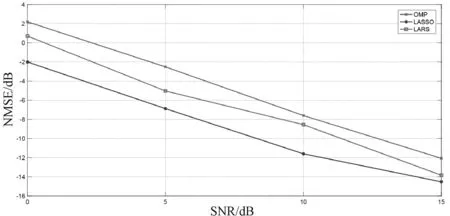
图2 基于Saleh-Valenzuela 信道模型的ULAs NMSE 性能比较

在图3 中,笔者进一步比较了OMP 算法、改进LASSO 算法和AMP 算法在不同信噪比下的NMSE 性能。 如图3 所示,随着信噪比增加,波束空间信道估计精度逐渐提高。 与传统的OMP 算法相比,AMP 算法和所提出的改进LASSO 算法在所有考虑的信噪比区域都具有更低的估计误差。 而且AMP 算法和所提出的改进LASSO 算法具有相似的NMSE 性能。 仿真结果表明,LARS 算法和所提出的改进LSSSO 算法能够获得比传统OMP 算法有更好的波束空间信道估计精度。

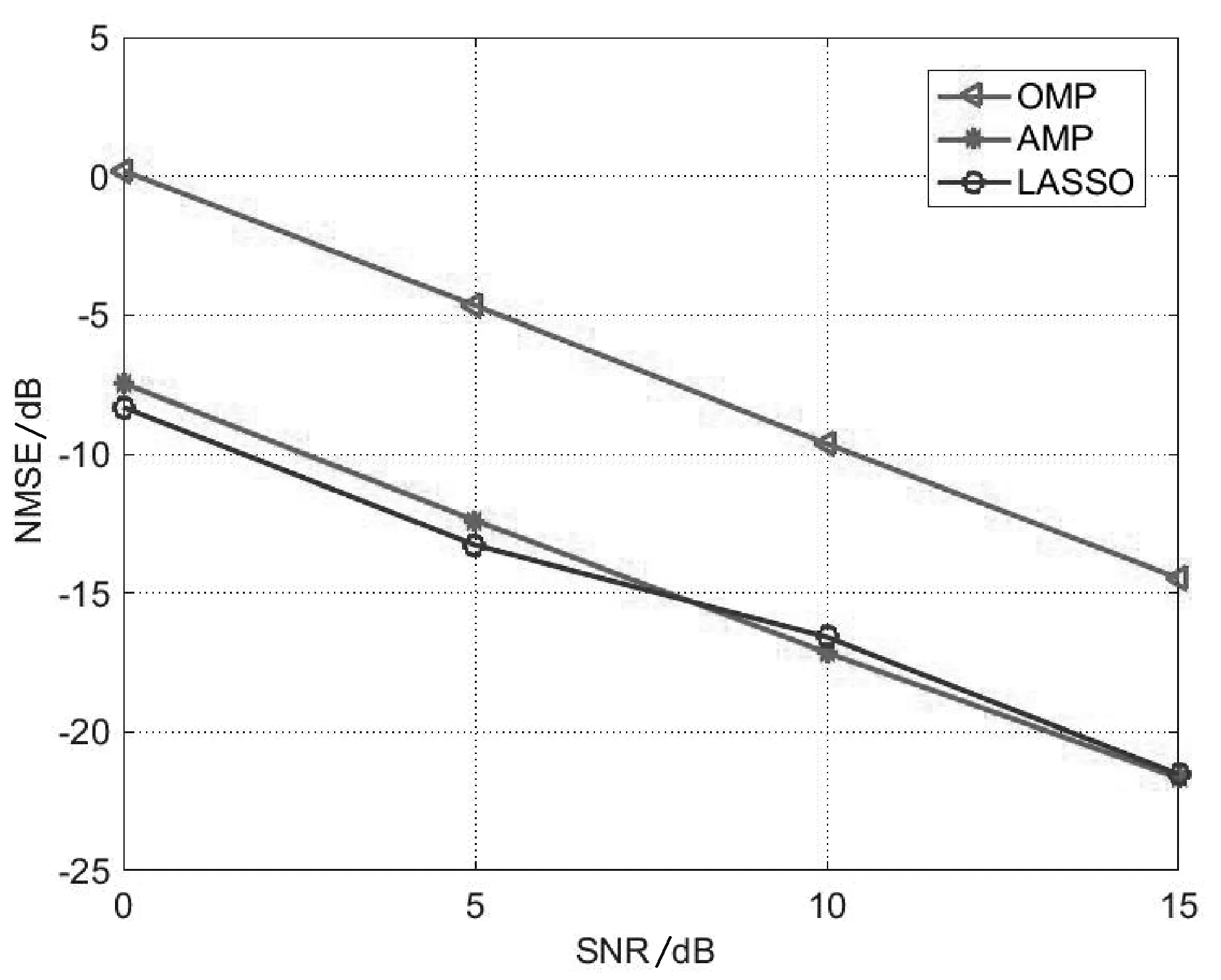
图3 基于Saleh-Valenzuela 信道模型的ULAs NMSE 性能比较

4 结语

本文提出了基于LARS 算法和改进LASSO 算法来解决毫米波大规模MIMO 系统中的波束空间信道估计问题。 仿真结果表明,与现有的OMP 和其他传统的波束空间信道估计方案相比,考虑基于LARS算法和改进LASSO 算法的信道估计能够以较低的导频开销获得更好的估计精度。 在未来的工作中,笔者将遵循所提出的LARS 算法的思想,通过考虑太赫兹信道特性来解决太赫兹通信中的信道估计问题。