基于改进狼群算法的AGV路径规划
程 俊, 董学平, 张志军
(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.工业自动化安徽省工程技术研究中心,安徽 合肥 230009)
随着社会经济发展和工业智能信息化的深入,智能化物流逐渐成为商业和工业领域必不可少的基础设施,这使得自动引导小车(automated guided vehicle,AGV)得到越来越广泛的应用,同时也促进了对AGV关键技术的深入研究。路径规划作为该领域核心技术之一,具有非常广泛的应用场合,比如手机导航、无人驾驶车辆的避障和规划路径、智能物流等。
针对路径规划问题,国内外学者做了大量的深入研究,提出了很多解决方法,其中包括遗传算法[1]、蚁群算法[2]、粒子群算法[3]和神经网络[4]等。其中,文献[5]基于狼群捕猎过程中的分工协作提出了狼群算法(wolf pack algorithm,WPA),该算法将狼群的捕猎活动抽象为游走、召唤、围攻3种行为,并引入“胜者为王”的头狼选择机制和“适者生存”的更新机制。狼群算法的提出引起了国内外学者的广泛关注。文献[6]将狼群算法成功应用于无人机航迹规划;文献[7]在原始狼群算法的基础上引入次头狼召唤和围攻的更新策略,提高了算法的全局寻优能力,并将其应用于空战目标火力分配问题上;文献[8]提出了根据游走次数的奇偶性改变探狼搜索方向的方法,并且引入自适应调节搜索步长的策略,提高了算法的求解精度。
狼群算法作为群体智能算法的一种,具有广泛的应用领域,同样也适用于AGV最优路径求解问题。本文针对狼群算法易陷入局部最优、搜索效率低等问题,提出了一种改进狼群算法(improved wolf pack algorithm,IWPA),并将其应用于AGV路径规划。本文介绍了AGV运动空间的环境建模以及改进的狼群算法,比较了IWPA和WPA在函数优化问题上的求解效果,并对2种算法分别进行了AGV路径规划仿真实验和结果分析。
1 AGV路径规划问题
1.1 环境建模
在AGV路径规划研究中,描述环境的建模方法有很多种,常用的有可视图法、自由空间法、拓扑法和栅格法等[9-11]。本文采用栅格法进行环境建模,将运动环境映射成大小相同的网格矩阵,每块栅格的边长都为1,AGV视作地图中的一个质点。一个5×5的栅格环境如图1所示,以栅格左下角为坐标原点,横向为X轴,竖向为Y轴,则栅格j的坐标为(aj,bj)。对地图中的栅格采用实数编码,则在M×M的栅格环境中,栅格坐标与编号N的对应关系为:
(1)
其中:mod为取余运算;fix为向靠近取整的运算。
带障碍物的栅格地图如图1所示,AGV路径规划即要求在图1中白色的可行区域内规划出一条从起始点到目标点的最优路径。
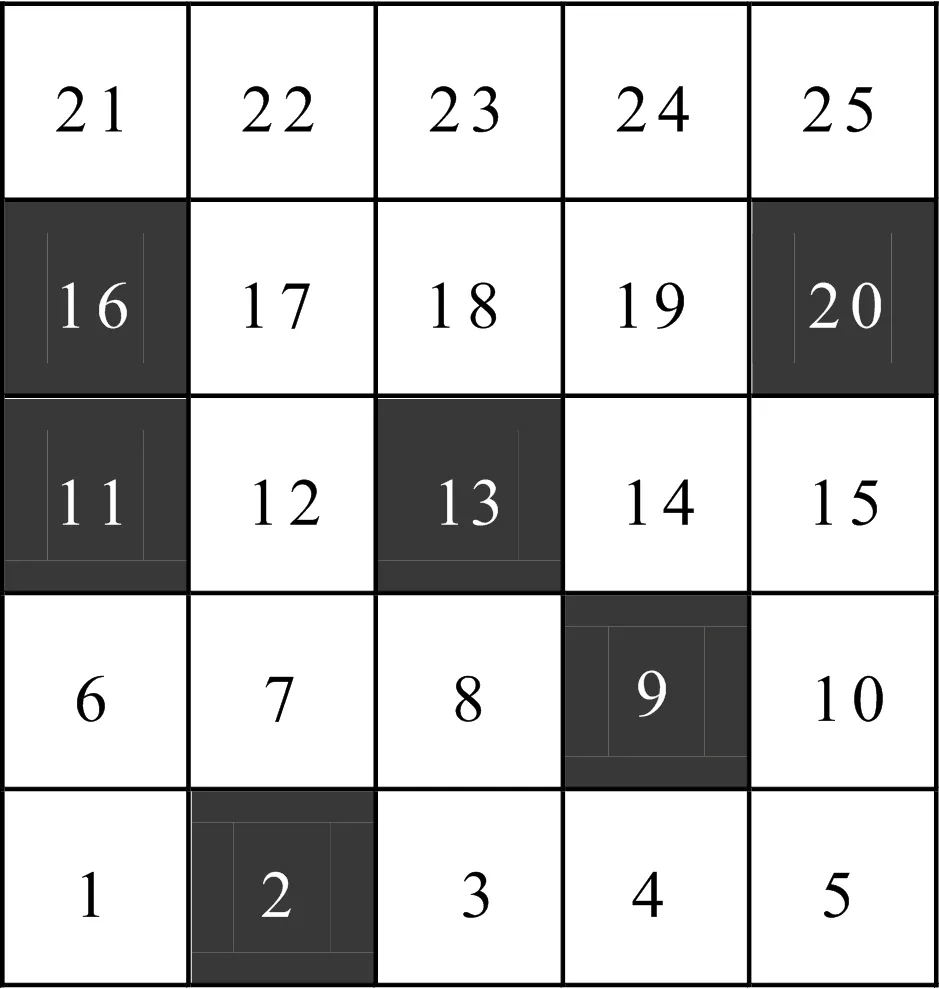
图1 带障碍物的栅格地图
1.2 适应度函数的建立
利用狼群算法进行路径规划时,种群中的每匹狼都代表一条潜在的可行路径,适应度函数则是评价这条路径优劣程度的唯一标准。本文适应度函数采用路径长度、平滑度以及安全度作为评价指标。
1) 路径长度评价函数f1。计算公式为:
(2)
其中:a、b为当前路径中所经过栅格的位置坐标;t为路径节点个数。
2) 路径平滑度评价函数f2。采用相邻路段之间夹角之和的大小作为评价平滑度的指标,即
(3)
其中,θ(ljlj+1,lj+1lj+2)为相邻2条路段ljlj+1和lj+1lj+2的夹角。f2值越小,路径越平滑。
3) 路径惩罚函数f3。路径与障碍物相交的次数越多则函数值就越大,越容易在迭代过程中被淘汰。
(4)
其中:m为与障碍物相交的次数;C为一个取值较大的正常数。
将f1和f2进行归一化处理后,AGV路径规划的适应度评价函数为:
f=μ1f1/dpath+μ2f2/(180°Nnum)+f3
(5)
其中:dpath为起点和终点与它们之间垂直交叉点的距离之和;Nnum为路径的拐点总数;μ1、μ2为权值,且μ1+μ2=1。
故AGV的最优路径规划即为求解使适应度函数f最小的坐标集。
2 改进的狼群算法
2.1 狼群算法基本原理
狼群算法的基本过程主要包括以下步骤:
1) 狼群初始化。在D维空间中随机初始化n匹人工狼的位置,则第i匹人工狼的位置可表示为Xi=(xi1,xi2,…,xiD),i=1,2,…,n。
2) 选取距离猎物最近的人工狼为头狼,并将除头狼外最优的S-num匹狼选取为探狼,S-num随机取[n/(α+1),n/α]中的整数,α为探狼比例因子,并执行游走搜索行为,向四周h个方向以步长Sa搜寻猎物。探狼i向第p(p=1,2,…,h)个方向游走后,在第d维空间位置更新为:
(6)
若探狼搜索到距离猎物更近的位置,则更新其当前位置,并重复游走行为,直到某人工狼搜索到优于头狼的位置时,该探狼将代替头狼发起召唤或直到游走达到最大游走次数Tmax。
3) 将头狼和探狼以外的其余狼作为猛狼,在头狼发起召唤后,猛狼以步长Sb向头狼移动,猛狼i在第k+1次迭代后,其在第d维空间位置更新为:
(7)
在奔袭的过程中,若猛狼所处位置优于头狼,则该猛狼将代替头狼发起召唤行为;否则猛狼将继续奔袭,直到与头狼的距离小于dnear时,对猎物发起围攻。判定距离dnear的计算公式为:
(8)
其中:ω为距离判定因子;dmax、dmin为狼群在第d维空间位置坐标的最大值和最小值。
4) 当猛狼与猎物的距离小于dnear时,便联合探狼以步长Sc对猎物进行围攻,以期捕获。狼群位置更新公式为:
(9)
其中,λ为[-1,1]间均匀分布的随机数。若进行围攻之后人工狼离猎物更近,则更新位置;否则保持原位置不变。
3种搜索步长在第d维空间中存在如下关系:
(10)
其中,S为步长因子。
5) 狼群的更新机制。根据适者生存的更新策略,淘汰适应度最差的R匹狼,然后随机生成R匹狼。R为随机整数,取值在[n/(2β),n/β]之间,其中β为比例因子。
2.2 狼群算法的改进
针对传统狼群算法初始种群多样性不足,探狼游走方向固定,易陷入局部最优,迭代后期搜索效率低等缺陷,本文从如下4个方面进行了改进,以进一步提高算法的寻优效率。
2.2.1 改进的Sine混沌映射优化初始种群
狼群算法中种群的初始位置和狼群的更新机制均采用随机生成的方式,这种方式容易导致种群分布不均匀、多样性不足,影响后期的迭代寻优效率。而混沌映射具有遍历性、规律性、随机性等特点,可以有效避免这些缺陷。
产生混沌变量的Sine混沌模型映射公式为:
zk+1=φsin(πzk)
(11)
其中:zk为迭代序列,k∈N,z0∈(0,1];φ为控制参数,φ越接近1时混沌性能越好。
当取φ=1,迭代2 000次后,Sine混沌映射序列分布图如图2、图3所示,可以发现序列的分布并不十分均匀,在[0,0.1]和[0.9,1.0]区间内出现的频率较高。

图2 Sine映射分布直方图

图3 Sine映射分布图
依据文献[12]所提方法对Sine混沌映射进行改进,如式(12)所示,并利用式(13)将序列映射到狼群空间位置上。
(12)
xid=dmin+yid(dmax-dmin)
(13)
其中:y∈[0,1]为混沌迭代序列;φ为控制参数。
改进后的Sine映射分布图如图4、图5所示。从图4、图5可以看出,混沌值分布更加均匀,出现的概率更加相近。因此采用改进的Sine映射进行狼群初始化和更新,有利于提高种群多样性,进而提高算法的寻优效率。
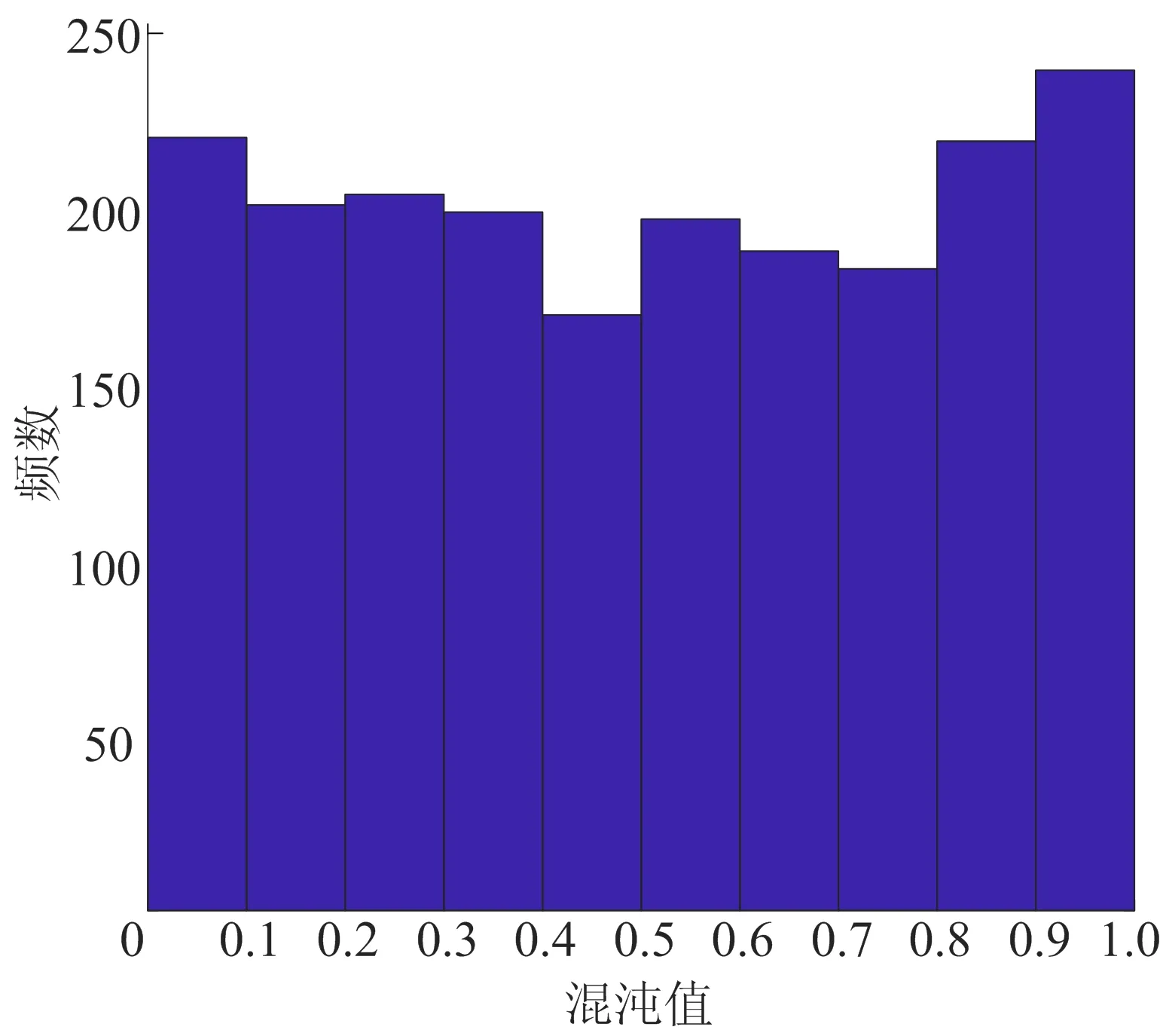
图4 改进的Sine映射分布直方图

图5 改进的Sine映射分布图
2.2.2 探狼随机游走策略
在传统的狼群算法中,探狼游走行为由式(6)决定,这使得探狼i不论迭代搜索多少次,方向只有h个,搜索方向固定,且每代之间的搜索方向都是平行的,削弱了算法的随机性。文献[8]提出根据游走次数的奇偶性改变搜索方向的方法,文献[13]在游走行为中引入相位因子,以提高探狼搜索的灵活性。为了进一步丰富搜索方向,本文对探狼游走公式进行了改进,公式如下:
(14)
其中,v为随机方向向量,计算公式为:
v=V(:,p)T,V=rand(D,h)
(15)
其中,rand为生成随机数的运算。
这样探狼在每次游走时,会随机选择h个方向进行搜索,方向不固定,增强了搜索的随机性,从而提高了算法的全局寻优能力。
2.2.3 头狼选择引入Metropolis准则
原始算法中总是选择适应度最好的人工狼作为头狼,执行召唤行为。在迭代后期,种群多样性降低时,易使种群陷入局部最优,降低算法的全局搜索能力。针对该问题,在探狼游走搜索后,对头狼的选择方式上引入Metropolis准则[14]使得算法具有概率突跳的能力。
本文以种群迭代次数k来表示Metropolis准则中的温度,改进公式为:
(16)
其中,Kmax为种群最大迭代次数。
当探狼i搜索到优于头狼的位置时,探狼i取代当前头狼发起召唤;当所有探狼搜索至最大游走次数依然未搜索到优于头狼的位置时,按式(16)概率接受非最优人工狼作为当前种群的头狼,随着迭代次数的增加,算法接受非最优人工狼作为头狼的概率逐渐减小。
2.2.4 猛狼奔袭策略的改进

(17)
其中,λ为[0,1]内的随机数。
2.3 改进狼群算法步骤
1) 采用栅格法对AGV运动环境进行建模,对栅格进行编码,并获取障碍物信息。
2) 采用实数编码,对狼群进行初始化。利用2.2.1节所述方法构造人工狼初始位置,则第i匹人工狼位置为Xi=(xi1,xi2,…,xiD),i=1,2,…,n,每匹人工狼代表一条潜在的可行路径;初始化算法的迭代次数Kmax、探狼比例α、狼群更新比例β、游走步长Sa、奔袭的步长Sb等。
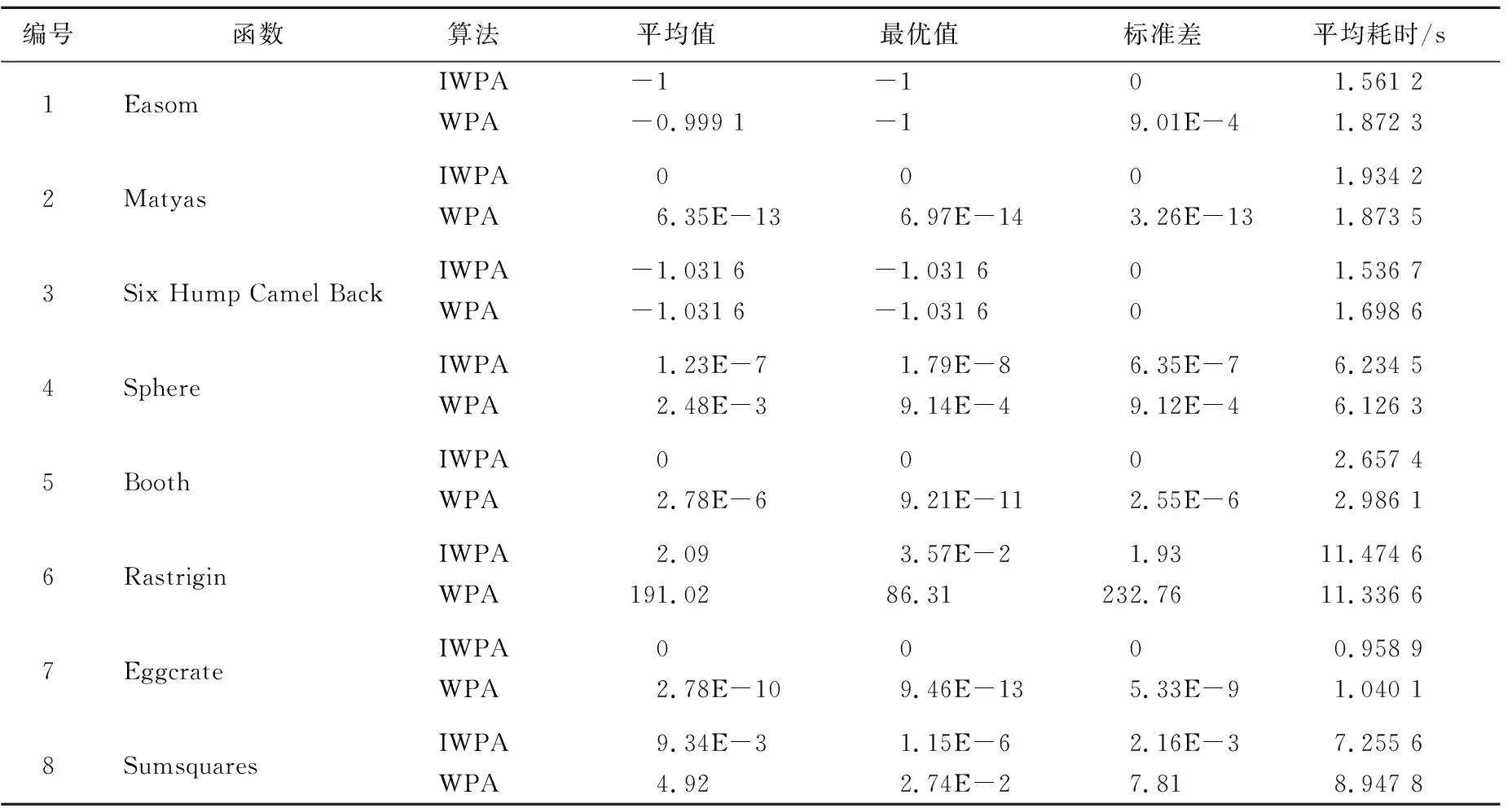
3) 按照式(5)计算每匹狼的适应度f(Xi),将适应度最好的人工狼暂定为头狼,除头狼外适应度最好的前S-num匹狼作为探狼。按照式(14)执行游走搜索,若f(Xi) 4) 猛狼按式(9)向头狼奔袭,若途中发现适应度优于头狼,则将取代头狼发起召唤。 5) 猛狼联合探狼按式(17)执行围攻行为。 6) 更新头狼位置,并淘汰掉适应度最差的R匹狼,按改进的Sine混沌映射规则重新生成R匹狼。 7) 判断是否满足终止条件,若满足,则算法结束;否则转至步骤3)继续进行搜索。 为了验证本文所提的IWPA的有效性和可行性,本文选择了在函数优化中广泛使用的8个标准测试函数进行测试,并与WPA进行实验对比。测试函数的基本信息见表1所列,表1中:U表示此函数为单峰;M表示多峰;S表示可分;N表示不可分。 实验设置最大迭代次数为1 000,种群数量为100,探狼比例因子α=4,狼群更新比例因子β=5,ω=500,S=100,其他参数参考文献[5]设置,分别进行100次的独立实验。实验结果见表2所列,若结果小于1E-16,则视为0。 表1 8个标准测试函数 表2 函数优化结果对比 由表2可知,首先在平均值与最佳值的对比上,IWPA比WPA寻优能力更强,收敛精度更高。对Eason、Matyas单峰函数寻优接近理论最优值,体现了IWPA具有较强的开采能力,这得益于种群的多样性以及猛狼良好的围攻行为;对Rastrigin、Sumsquares等多峰函数具有较好的优化效果,体现了IWPA跳出局部极值的能力,这得益于对头狼的选择上引入了Metropolis准则,使得算法具有概率突跳的能力。从标准差的对比可以看出IWPA具有更好的鲁棒性,在平均耗时上IWPA与WPA处于同一级别,说明IWPA在提升性能的基础上并没有明显增加运行时间。 为了更直观地说明IWPA的优越性,给出了Rastrigin、 Eggcrate、Sumsquares 3个函数的收敛曲线,如图6所示。从图6可以看出,IWPA在收敛速度和求解精度上均有优势。 为了验证改进的狼群算法在AGV路径规划问题上的可行性,本文进行了仿真实验。仿真环境为20×20的栅格地图,起始坐标为(0,0),终点坐标为(20,20),种群维数为18,种群个数N=100,最大迭代次数K=200,探狼比例因子α=4,狼群更新比例因子β=5,最大游走次数T=10,步长因子s=20,μ1=3/5。在相同的条件下,将IWPA和WPA 2种算法各自运行100次,路径规划的数据统计结果见表3所列,各自规划的最优路径如图7、图8所示。 表3 2种算法运行100次的数据比较 图7 WPA的最优路径规划 图8 IWPA的最优路径规划 从表3可以看出,在仿真环境中,IWPA规划的最优路径距离比WPA的短1.7 m左右,总转角度数小45°,从平均值和方差上可以看出IWPA寻优更加稳定、鲁棒性更好。从图7和图8可以看出IWPA规划的路径更加平滑,充分说明了IWPA在AGV路径规划上的有效性和稳定性。 本文在栅格法环境建模的基础上,针对AGV路径规划问题,提出了一种改进的狼群算法。该算法利用改进的Sine混沌映射进行种群的初始化和更新,提高了种群的多样性;探狼的随机游走策略,增强了算法搜索的随机性;在头狼的选择上引入Metropolis准则,提高了算法跳出局部最优解的能力;猛狼奔袭策略的改进有利于加快算法收敛。仿真实验表明,在AGV路径规划的问题上,IWPA比WPA更加有效,具备一定的实用价值。3 仿真实验
3.1 函数测试与分析

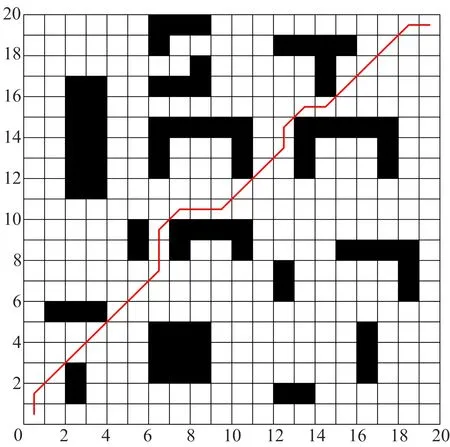
3.2 路径规划仿真实验


4 结 论

