联合SIFT-GPU和整体平差法的隧道影像拼接研究

张栋樑, 宫志群, 杨世廷, 陆业宁, 占 静, 安晓亚

(1. 中国建设基础设施有限公司, 北京 100029; 2. 武汉天际航信息科技股份有限公司, 湖北 武汉 430074; 3. 西安测绘研究所, 陕西 西安 710054; 4. 地理信息工程国家重点实验室, 陕西 西安 710054)

0 引言

影像拼接是指将2张或2张以上具有重叠区域的影像,通过坐标系之间的变换关系,拼接成1张视场更大、信息更丰富的影像[1]。目前已广泛应用在城市街景影像拼接、卫星影像拼接等领域。隧道受光照等因素限制,比普通道路巡检更加复杂,利用车载移动测量技术和影像拼接技术获取隧道内壁影像,可为其内壁安全巡检工作提供新的巡检手段。影像匹配是影像拼接过程中最耗时的环节之一,常用的影像匹配算法包括SIFT算法[2-3]、SURF(speeded up robust features)算法[4-5]。Mikolajczyk等[6]选取了10种算子,在光照变化、几何变形等6种不同情况下对其进行测试与比较,发现SIFT算子匹配效果最好。后续有多位学者使用SIFT算法进行影像匹配。例如: 周杰等[7]使用SIFT算法和泊松融合对无人机遥感影像进行融合; 张冬梅等[8]结合SIFT算法、LM(Levenberg-Marquardt)法和RANSAC算法进行特征点匹配和误匹配点剔除,并将最小生成树算法引入到拼接路径中,实现了影像的有效拼接; 喜文飞等[9]利用SIFT算法和改进的RANSAC算法进行影像拼接,提升了影像匹配点粗差剔除率; Dong等[10]采用SIFT算法提取图像中的特征点,并利用LATCH描述符和RANSAC算法对特征点进行描述和误配点剔除,最后利用平移单应矩阵拼接图像,解决了影像拼接中的黑线问题。但随着待拼接影像数量的增加,SIFT算法存在匹配效率低的问题。如何有效提升影像匹配速度是影像拼接研究中亟待解决的问题之一。

此外,误差累积是影像拼接过程中的另一问题。Ait-Aoudia等[11]使用影像间同名点的均方根误差评价拼接结果。何敬[12]通过分块拼接,采用最优拼接路径的方法减少误差累积。张冬梅等[8]通过SIFT算法进行特征点匹配,采用LM方法和RANSAC算子剔除误匹配点,有效减少了影像拼接过程中的误差累积。岳广等[13]利用航空平台的姿态信息和位置信息完成了各图像的投影变换和图像粗拼接,有效减少了误差累积。然而,以上算法多考虑相邻影像间的误差关系,未考虑待拼接影像的整体关系,误差会随着拼接次数的增加而逐渐累积。

基于以上问题,本文联合SIFT-GPU协同处理算法和整体平差法进行隧道影像拼接试验研究。在隧道影像匹配过程中,融合SIFT匹配算法和GPU-CPU协同处理技术[14],通过分解SIFT算法处理过程,将其中可以并行处理的步骤通过GPU加速运算,提高影像匹配效率。在影像配准过程中,使用整体平差算法整体求解待拼接影像的变换参数,降低传统算法中因拼接次数增加而导致的误差累积问题。

1 数据采集与预处理

1.1 隧道影像数据采集

研究使用车载移动测量平台(见图1)采集隧道内壁数据,其搭载有全景相机、陀螺仪、Lidar、计步器和人工光源5个硬件模块。全景相机为4镜头相机; 陀螺仪用于获取外方位元素; Lidar用于获取隧道内壁点云; 计步器用于控制相机快门和计算所拍摄的相邻2站影像的重叠度; 人工光源为相机拍摄提供辅助光源支持。作业时,汽车搭载设备沿道路中轴线以10 km/h的速度前进,每前进2.5 m拍摄一次;Lidar在汽车前进过程中连续扫描。

图1 车载移动测量平台Fig. 1 Vehicle-mounted mobile measuring platform

1.2 隧道影像数据预处理

1.2.1 隧道影像纠正

受拍摄过程中影像倾斜和被摄景物的深度影响,可能存在影像变形。使用Lidar点云数据对原始影像进行初步纠正。使用Lidar采集到的隧道点云数据建立隧道内壁模型,基于成像点和其对应物方点的共线方程进行影像纠正,最后选用双线性内插法对纠正后的影像进行灰度内插和赋值,得到纠正后的影像。隧道影像纠正过程如图2所示。

1.2.2 隧道影像匀光匀色

隧道内部的特殊环境决定了必须使用人工光源辅助影像拍摄,但人工光源强度有限,辐射不均匀,需对其进行匀光匀色处理。

1.2.2.1 MASK匀光算法

采用MASK匀光算法对单张隧道影像进行处理,保证单张隧道影像中间与边缘亮度一致[15],算法公式为式(1)—(3)。

(1)

(2)

(3)

1.2.2.2 Wallis滤波匀光法

采用Wallis滤波匀光法对所有隧道影像进行处理,保证隧道不同影像间色调一致[16],公式如式(4)所示。

(1-b)mg。

(4)

式中:w(x,y)为Wallis匀光后的影像;g(x,y)为原始影像;mg为原始影像的局部灰度均值;c为影像方差的扩展常数,c∈[0,1];Sf为匀光后影像局部灰度标准偏差的目标值;Sg为原始影像的局部灰度标准偏差;mf为匀光后影像局部灰度均值的目标值;b为影像的亮度系数,b∈[0,1]。

2 基于特征点的隧道影像匹配

2.1 基于SIFT匹配算法的GPU-CPU协同处理

影像匹配的目的是寻找2张或多张影像之间的同名点或同名直线。GPU-CPU协同处理是: CPU作为控制中心负责数据的传输、GPU的调用和并行程度低的计算等串行程序的执行; GPU负责并行程度高且耗时长的大规模计算,并将计算结果输出到CPU。依据各自运算的特点和SIFT匹配算法的关键步骤可以发现,影像的读取、高斯核函数的计算、DOG(difference of Gaussian)金字塔的建立、候选关键点位置的确定、特征向量的提取等需要依靠CPU来完成;而高斯金字塔的建立、关键点位置的确定以及SIFT特征向量的匹配等并行程度高的计算步骤可以利用GPU加速运算,简称为SIFT-GPU匹配算法。其计算方案如图3所示。

图3 SIFT-GPU匹配算法具体计算方案Fig. 3 Detailed calculation scheme of SIFT-GPU matching algorithm

2.2 基于RANSAC算法的误配点剔除

得到基准影像与待配准影像的特征点后,需完成2张或多张影像间特征点的一一匹配。SIFT算法采用基于欧氏距离的最邻近匹配法进行粗匹配,虽能去除一些外点,但仍会存在少量误配点。为得到影像间精确的变换矩阵,采用RANSAC算法对误配点进行剔除。其主要思想是基于某一模型,通过反复随机提取处理数据的子集来估计模型参数,通过设置阈值将处理数据分成“内点”和“外点”,将对应“内点”数目最多的模型参数视为最优模型参数[17-18]。RANSAC算法流程图如图4所示。

图4 RANSAC算法流程图Fig. 4 RANSAC algorithm flowchart

3 隧道影像拼接模型

3.1 拼接模型选择

常用的影像拼接模型有平移旋转缩放变换、仿射变换、透视变换、非线性变换等[12,19]。不同影像拼接模型的几何特征不同,所能够消除的变形类型也有所不同。隧道内壁的形状类似于柱面而非平面,但人们在观测二维影像时通常习惯于观测平面视觉的影像,在后续拼接模型选择中充分考虑人们的视觉习惯和拼接精度。

3.2 基于GLS算法的影像配准整体平差

使用普通最小二乘法(LS算法)求解2张待拼接影像的误差方程时,会默认为一张影像上的特征点(xi,yi)具有误差,另一张影像的特征点(xi′,yi′)完全正确。这会造成变换参数的有偏估计,在影像数量较少的情况下,对结果影响不明显,但随着影像数量的增多,在影像连续拼接中会造成误差累积。广义最小二乘法(GLS算法)通过为解释变量加上一个权重,可以得到误差的无偏和一致估计。本文使用整体平差法,即在整个待拼接区域中,对所有具有重叠区域的影像进行匹配,将匹配出的所有同名点全部纳入平差,整体求解变换参数,整个过程只需进行1次平差。

以仿射变换作为拼接模型为例对整体平差算法进行说明。对于整个待拼接区域的所有影像,可将它们之间的重叠关系分为2类: 1)重叠像对中包含基准影像; 2)重叠像对中不包含基准影像。以第1张影像作为基准影像,如果影像与其具有重叠区域,则误差方程可用矩阵表示为:

(5)

式中: (x1,y1)和(xi,yi)为影像I1与Ii上的一对同名点;a1i,0、b1i,0、c1i,0、d1i,0、e1i,0、f1i,0为影像Ii变换参数的初值;vx和vy分别为x和y的误差;Da1i、Db1i、Dc1i、Dd1i、De1i、Df1i为影像Ii变换参数的绝对偏差。

如果影像Ii和Ij(i≠1,j≠1)具有重叠区域,则该像对上所有同名点的坐标值在基准影像所在坐标系上的坐标值完全相等,误差方程可用矩阵形式表示,如式(6)所示。

(6)

式中: (xi,yi)和(xj,yj)为影像Ii与Ij上的一对同名点;a1j,0、b1j,0、c1j,0、d1j,0、e1j,0、f1j,0为影像Ij变换参数的初值;Da1j、Db1j、Dc1j、Dd1j、De1j、Df1j为影像Ij变换参数的绝对偏差。

如果有m+1张影像参与拼接,共匹配出n对同名点,则可以列出2n个误差方程,误差方程用矩阵形式表示为:

(7)

4 试验与结果

4.1 隧道影像匀光匀色试验

试验样本为经过预处理后的若干张某隧道内侧壁的影像。采用MASK匀光算法对单张隧道影像进行匀光处理。图5(a)为典型的“中间亮、四周暗”的隧道影像,图5(b)为经MASK匀光后的隧道影像,匀光后光照均匀。

采用灰度均值、信息熵、标准差、平均梯度4种图像质量评价指标,评价MASK匀光后的影像在R、G、B通道下的变化,结果见表1。由表可以发现,采用MASK匀光算法改善了隧道影像的光照强度,影像反差变小,图像清晰度得以提高。

表1 MASK匀光前后图像质量评价指标对比Table 1 Comparison of evaluation indexes before and after smoothing light using MASK algorithm

采用Wallis匀光算法进行色差调整。图6(a)和图6(b)为经过MASK匀光处理后的位于隧道不同地段的2张影像,光照都很均匀,但图6(b)相对于图6(a)明显偏暗。因此,以图6(a)为基准影像对图6(b)进行Wallis匀光,结果如图6(c)所示。对比图6(a)和图6(c)可知,经过Wallis匀光后的影像与基准影像的色调一致。

(a) 基准影像 (b) 待匀光影像 (c) Wallis匀光后的影像图6 Wallis匀光前后的隧道影像对比图Fig. 6 Comparison of tunnel imaging before and after smoothing light using Wallis algorithm

使用上述4种指标对Wallis匀光结果进行评价,结果见表2。由表可见: Wallis匀光后隧道影像亮度与基准影像十分接近,影像反差变小。

表2 Wallis匀光前后图像质量评价指标对比Table 2 Comparison of evaluation indexes before and after smoothing light using Wallis algorithm

4.2 隧道影像匹配试验

将已被纠正且进行匀光匀色处理后的隧道影像进行匹配处理,采用原始SIFT算法和SIFT-GPU算法分别进行匹配试验。为验证不同条件下的匹配效果,分别选用3组纹理、光照、尺寸等特点不同的隧道影像进行试验。试验采用的硬件平台: CPU为Intel Core i5-3470 3.20 GHz,GPU为NVidia GeForce GTX 650。试验采用的软件平台为: Microsoft Windows 10,Visual Studio 2010。

4.2.1 试验1

选用2张具有一定重叠度、隧道内壁纹理丰富、光照充足、辨识度高的影像进行匹配试验,影像大小均为3 000×2 000,匹配结果如图7和表3所示。由结果可知: SIFT-GPU匹配算法的运算时间显著减少,RANSAC算法能够较好地剔除影像中的误配点,提高后续拼接精度。

(a) SIFT-GPU匹配结果

(b) 剔除误配点后的匹配结果图7 试验1的影像匹配结果Fig. 7 Image matching results in experiment 1

表3 隧道影像匹配试验结果Table 3 Tunnel image matching experiment data

4.2.2 试验2

选用2张具有一定重叠度、内壁纹理单一、光照不足、辨识度低的隧道影像进行匹配试验,影像大小为2 000×3 600。匹配结果如表3和图8所示。由结果可知: 试验2相比试验1加速比小,原因在于内壁纹理单一的影像匹配出的同名点数量明显减少。由此也可以发现,SIFT-GPU匹配算法在特征明显的复杂影像匹配中效率优势更加明显。

(a) SIFT-GPU匹配结果 (b) 剔除误配点后的匹配结果图8 试验2的影像匹配结果Fig. 8 Image matching results in experiment 2

4.2.3 试验3

选取2张尺寸更大、特征更加明显的隧道影像进行匹配试验,影像大小为7 952×5 304,匹配结果如表3和图9所示。由结果可知: 与试验1相比,加速比有一定降低,这与匹配出的同名点数量增加有关,但SIFT-GPU匹配算法的运算时间仍明显小于SIFT匹配算法的运算时间。

(a) SIFT-GPU匹配结果

(b) 剔除误配点后的匹配结果图9 试验3的影像匹配结果Fig. 9 Image matching results in experiment 3

4.3 隧道影像拼接试验

4.3.1 拼接模型选择试验

1.2.1节中影像初步纠正的共线方程的本质是透视变换,因此选择平移旋转缩放变换、仿射变换和二次多项式变换进行影像拼接试验。为对比3种影像拼接模型对于拍摄环境较为恶劣的隧道影像的拼接效果,选择纹理单一、重复率高、特征不明显的隧道影像进行试验。3种拼接模型的影像匹配对数量和误差值如表4所示。由表4可以看到: 3种拼接模型的匹配精度差别不大,二次多项式变换的拼接精度稍高。然而,隧道特殊的形态和成像环境使得影像的变形和基准影像特征十分复杂,如果完全继承这些特征,可能导致拼接结果误差值低,但缺乏观赏性与实用性。图10示出采用3种拼接模型对5张隧道影像的拼接结果。综合考虑拼接精度和拼接结果的可观赏性,选用平移旋转缩放变换模型对隧道影像进行拼接。

表4 3种拼接模型的影像匹配对数量和误差值Table 4 Number of image matching pairs and error value of three splicing models

(a) 二次多项式变换 (b) 仿射变换 (c) 平移旋转缩放变换图10 采用3种拼接模型对5张隧道影像的拼接结果Fig. 10 Comparison of five tunnel images with serious deformation by three splicing models

4.3.2 传统算法与整体平差算法对比试验

选用隧道侧面内壁的10张序列影像,采用平移旋转缩放变换模型对影像进行拼接,并分别使用传统平差算法和整体平差算法进行误差剔除,比较2种算法的误差结果(见表5)。由表可以看出: 整体平差算法的单位权中误差值是传统算法的1/3左右。表明采用整体平差算法进行误差剔除可有效提升影像拼接结果精度。

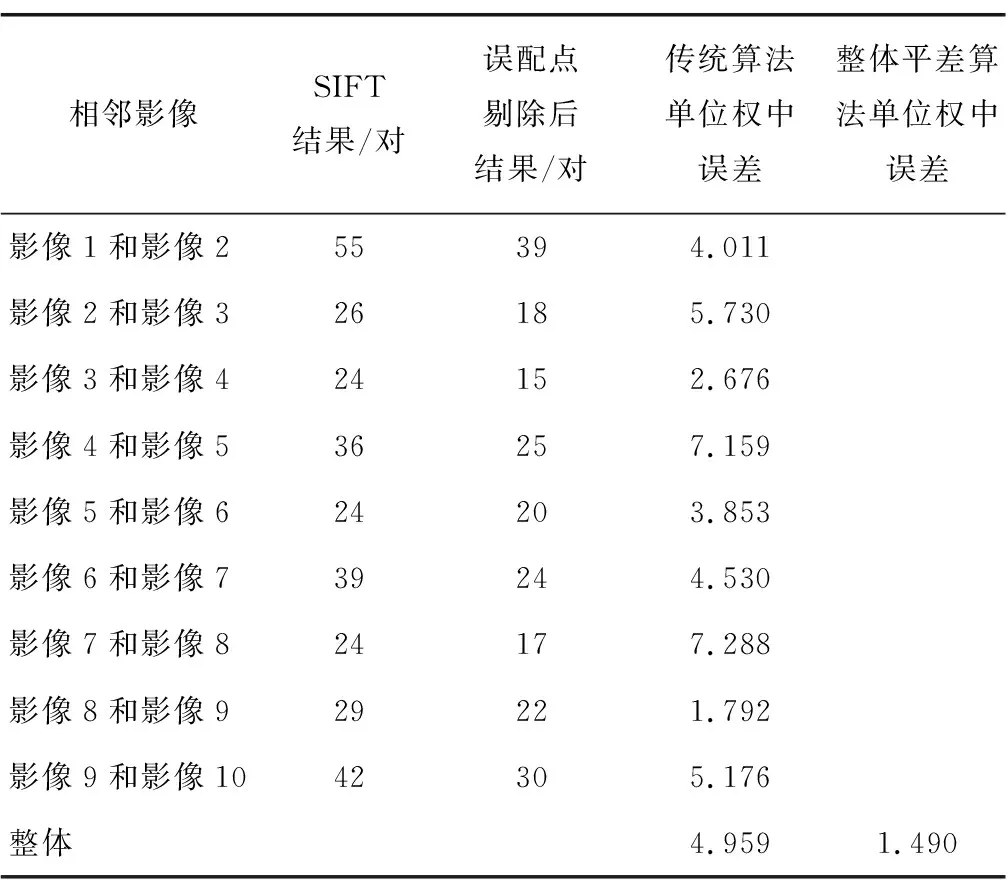
表5 10张隧道影像匹配对数量及2种算法的单位权中误差Table 5 Number of matching pairs of ten tunnel images and unit weight error of two algorithms

4.4 大范围隧道影像拼接结果

试验数据共包含400张隧道内壁的影像,隧道长度约为250 m,影像大小均为5 000×9 000。各阶段处理时间如表6所示。为防止影像拼接结果输出过程中计算机内存溢出,使用GDAL分块处理技术对影像拼接成果进行输出。图11(a)示出全景相机在某摄站拍摄的4张影像。首先,对所有摄站的4张影像进行拼接(见图11(b));然后,将拼接好的单站影像进行站与站之间的拼接,结果如图11(c)所示。最终拼接成果清晰地展示了该段隧道两侧壁、顶部以及部分地面纹理,整个拼接浑然一体,方便观察。

表6 影像拼接各阶段处理时间Table 6 Image processing process and corresponding time

(a) 某摄站的4张影像

(b) 单站4张影像的拼接结果

(c) 试验区域隧道所有影像拼接结果图11 试验区域隧道影像拼接结果Fig. 11 Tunnel image stitching process and final results

5 结论与讨论

针对隧道影像拼接问题,本文联合SIFT-GPU匹配算法和整体平差法进行了隧道影像拼接研究,并通过相关试验验证了该算法的有效性。

1)基于隧道内壁点云数据和匀光匀色算法对原始影像进行预处理,有效提高了待拼接隧道影像的质量。

2)选取3组纹理、光照、尺寸等特点不同的隧道影像进行拼接试验,结果表明,相比传统SIFT算法,研究使用的SIFT-GPU匹配算法使得影像匹配效率明显提升。

3)选取400张隧道内壁影像,使用平移旋转缩放变换模型、整体平差算法分别进行影像拼接和误差补偿,最终较好地呈现了隧道内壁的景观。相较于以往的研究,影像间衔接自然,无明显黑边,展示效果较好。

本文在影像匹配过程中引入GPU-CPU技术对提取所有待拼接影像特征点的效率进行了提升,然而并未对整个拼接过程的效率进行提升,下一步可继续研究影像拼接效率提升算法,进一步提升高分辨率长距离隧道影像的拼接速率。