脉搏波信号预处理方法研究
杨云龙, 杨海马, 赵晨阳, 张文婷, 宋智超, 石志介
(上海理工大学 光电信息与计算机工程学院,上海 200093)
脉搏波诊断又称脉诊,是中医诊断的一种重要方式,同时也在韩国、印度等东方国家的医疗保健中扮演着重要的角色[1]。传统脉诊依赖医生的主观评价,使得诊断结果往往存在争议,因此脉诊客观化显得尤为重要[2-3]。使用微型压力传感器采集桡动脉的寸、关、尺三部的脉搏波波形图分析脉象,是脉诊客观化的主要方式。而人体脉搏是一种微弱的信号,传感器直接采集的波形往往有较大的噪声,需要进行预处理后才能进行后续分析,预处理的好坏也直接影响了后续分析的准确与否。因此,对脉搏波预处理的方法进行研究具有重要的意义。
脉搏波信号是低频信号,采集到的信号中往往存在各种高频噪声,同时,采集的信号中也有部分低频噪声干扰,存在基线漂移的情况。因此,脉搏波信号预处理聚焦于解决上述两个问题:高频噪声干扰和基线漂移。对于高频噪声的去除,数字滤波器和小波阈值滤波器由于其使用简便、滤波效果较好,算力需求比目前流行的各类智能算法小,被广泛使用[4-8]。但设计的数字滤波器较复杂时,滤波后的信号可能会有一定的失真,需要进一步改进;使用小波阈值滤波器时许多关键参数需要人为确定,难以达到最佳滤波效果,需要进一步探讨。对于基线漂移的去除,常采用滤波器去除[9]、小波变换去除[10-11]、拟合基线去除[12-13]等这些计算量小、操作简便的方法,但是这些方法也各有利弊。
因此,本文介绍了去除高频噪声中相关参数的方法,建立了针对脉搏波的无参考信号的评价参数,并使用新研发的脉搏波采集手环采集多名受试者的原始脉搏波,着重探讨去除高频噪声的最佳方法。接着,对比了几种常用的去除基线方法的优缺点,从而确定最适合脉搏波信号的去除基线漂移方式。最后将上述两步骤最佳方法加以整合,得到脉搏波预处理的最佳方式。
1 脉搏波信号的预处理方法
1.1 脉搏波信号的基本特性
脉搏波作为人体较微弱的生理信号,其标准波形如图1所示,主要具有以下特性[9,14-15]。

图1 标准脉搏波波形图
① 低频性。脉搏波信号是低频信号,绝大多数在10 Hz以下。
② 差异性。脉搏波信号往往因受试者的年龄、状态等不同而存在差异,并没有一个绝对的标准信号,这点在评价滤波效果时需要着重考虑。
③ 信噪比低。采集得到的脉搏波十分微弱,往往会受到外界环境和人体自身的生理干扰。采集传感器的工频干扰是外界环境的干扰因素之一,由电力系统的交流电频率引起,会给信号带来高频噪声。人体自身生理干扰主要有测量时的人体呼吸频率带来的呼吸干扰,测量时身体的晃动带来的运动伪差干扰,以及测量时紧张造成的肌电干扰,这些干扰往往会给信号带来基线漂移干扰。
因此,脉搏波信号预处理环节就是要将高频噪声去除,并改善基线漂移现象。
1.2 去除高频噪声
1.2.1 数字滤波器
使用数字滤波器滤波是最基本的滤波方式,其利用离散系统的特性对信号进行转换,输出目标频率信号,抑制其他信号[16]。按冲激响应分类,数字滤波器可分为无限长单位冲激响应(Infinite Impulse Response,IIR)滤波器和有限长单位冲激响应(Finite Impulse Response,FIR)滤波器。
IIR滤波器有着与模拟滤波器相匹配的单位响应性质,利用成熟的模拟滤波器相关理论可使设计更加便捷[16]。通过选用合适的模拟滤波器模型并将模拟滤波器离散化转换为数字滤波器就可以完成IIR滤波器的设计。
FIR滤波器的设计方法主要有窗函数法、频率抽样法和最优化方法,其中窗函数法在时域中进行,后两种在频域中进行。窗函数法是使用最为广泛的方法,其将要求的理想频率响应Hd(ejω)利用离散傅里叶逆变换转换为时域上的理想冲击响应hd(n)后,使用一个有限长度的窗函数ω(n)来截断,从而得到有限长冲激响应序列h(n),即
h(n)=hd(n)·ω(n),0≤n≤N-1
(1)
式中:N为窗的长度;hd(n)为理想冲击响应,计算公式为
(2)
数字滤波器的设计较为简便,参数确定方法明确,滤除效果较好。但是在信号和噪声频带相互重叠的情况下,会将有效信号和噪声一起去除,从而丢失原有信息。同时若设计的滤波器较为复杂,滤波后的信号可能会存在相位延迟和自适应振铃噪声,需要加以改进。
1.2.2 小波阈值滤波去噪
小波变换则具有良好的时频局部化特性,在信号和噪声的频带相互重叠的情况下也可以很好地分离噪声并去除[17]。小波变换去噪的基本原理如下。
设长度为n的信号xn被噪声en所污染,所测得的含噪数据Xn为
Xn=xn+en
(3)
根据小波变换的线性特性可以得到变化后的含噪数据Xn,其为信号xn和噪声en小波变换之和。因此,对含噪数据Xn进行多尺度小波变换后,在各尺度下抑制噪声en的小波系数,保留信号xn的小波系数,最后重构即可实现去噪。其中,利用小波阈值收缩法实现对信号的保留和噪声的抑制是小波变换去噪中使用最广泛的方法,该方法在最小均方差意义下可达到近似最优[18]。
与传统的数字滤波器相比,使用小波阈值滤波去噪可以很好地处理噪声和信号的混叠,适应性更广。但是在使用此方法时需要确定大量参数,参数选择也无明确标准,这给设计带来一定的不便。
1.2.3 滤波效果评价
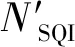
(4)
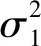
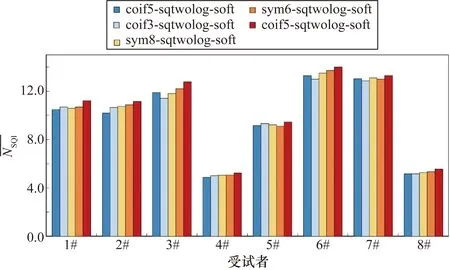
但是滤波前后数据的离散程度改变量较小,使得滤波前后的方差差异并不大,使用比值的方式定义评价参数会将差异进一步缩小。同时,方差的量纲和数据的量纲不一致,统计学描述波动一般使用的是标准差。因此,将评价参数定义修改为
NSQI=σ1-σ2
(5)
式中:σ1为滤波前信号的标准差;σ2为滤波后信号的标准差。σ2越小,则NSQI越大,代表滤波器的效果越好。
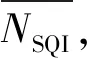
(6)
式中:NSQI,cun、NSQI,guan、NSQI,chi分别为寸部、关部、尺部信号的NSQI值。
1.3 去除基线漂移
常用于去除基线漂移的方法主要有滤波法、小波变换法、拟合基线法。
基线漂移主要由低频噪声引起,而脉搏波信号也为低频信号,使用滤波法容易损失低频信号。小波变换法和拟合基线法的去除基线效果基本相同[22],两者主要差异在于小波变换法的计算量稍低于拟合基线法,但拟合基线法可以将所有脉搏波周期的起始点和结束点拉至同一条直线上,小波变换法则无法做到。同时,拟合基线法可以预测未来短时间内的趋势,在信号的实时处理上具有优势。因此,对于脉搏波信号的基线漂移去除,采用拟合基线法最为适合。
2 预处理方案设计
2.1 实验材料
使用新研发的脉搏波手环[23]对预处理所需要的脉搏波信号进行采集,采集手环的硬件设计框图如图2所示。手环使用3枚DA17-01BA-00压力传感器同时高速采集寸、关、尺三部脉搏波信号,采样频率为200 Hz。采集到的数据通过通信模块的数据线或蓝牙可传输至上位机,可以使用手机或电脑端接收和分析数据。采集手环及电脑端采集的三部脉搏波如图3所示。
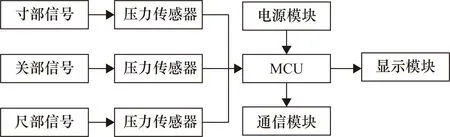
图2 采集手环的硬件设计框图
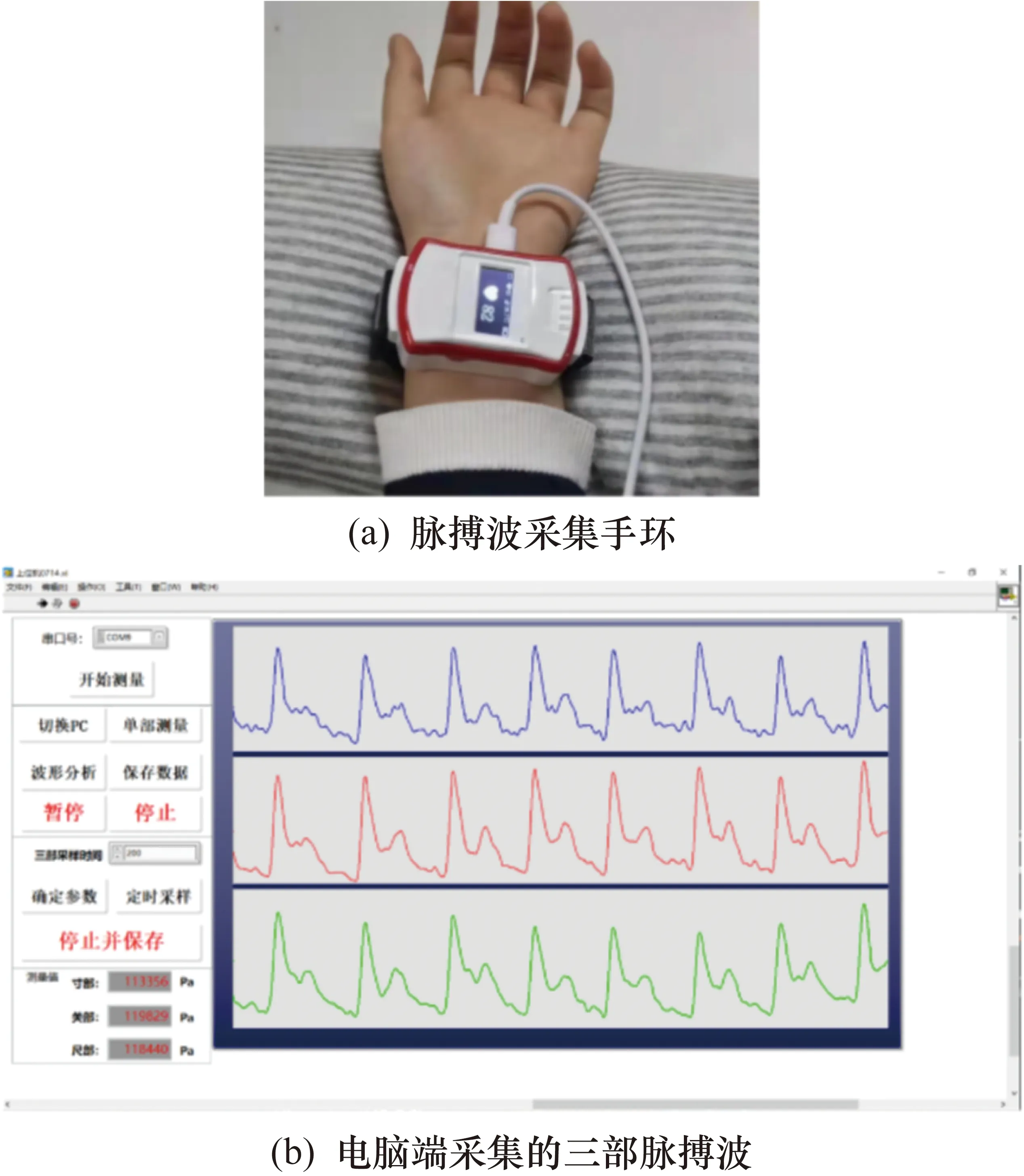
图3 脉搏波采集手环及电脑端采集的三部脉搏波
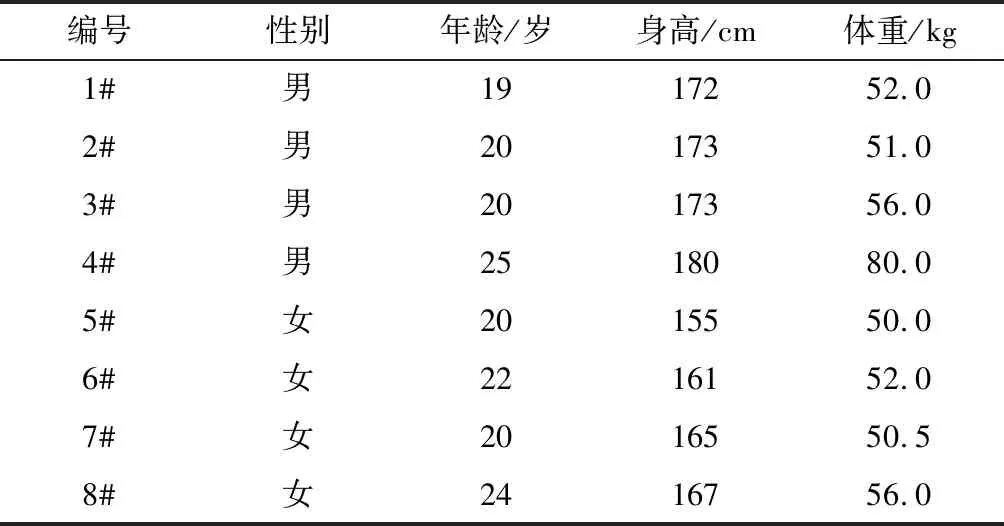
表1 受试者信息表
2.2 数字滤波器设计
IIR与FIR数字滤波器的设计流程已比较成熟,但是若设计的滤波器比较复杂,滤波后的信号可能会存在部分失真,而目前常用的处理方法较为烦琐,因此需要进一步改进。同时,设计过程中参数设定不当也会加剧滤波后信号的失真,因此需要再次明确参数的确定方法。
首先,要根据信号特点和实际情况确定滤波器参数。由于实际滤波存在过渡带,设计时还需考虑过渡带对信号衰减的影响。同时,过渡带也不能过窄,过窄的过渡带会引起幅度的陡峭衰减,产生振铃噪声[24]。因此,根据脉搏波信号的特点并考虑实际滤波器的特点得到设计低通滤波器的参数,其通带频率为15 Hz、阻带频率为30 Hz、通带波纹为1 dB、阻带衰减为70 dB。
接着,根据确定的滤波器参数设计滤波器。对于IIR滤波器而言,需要确定使用的滤波器类型。根据确定的滤波器参数,分别使用4种滤波器设计得到的幅频特性曲线如图4所示。从图4中可看出,4种滤波器中Butterworth滤波器在过渡带内衰减最快,没有通带波纹。因此,使用Butterworth滤波器来设计IIR数字滤波器最为合适。
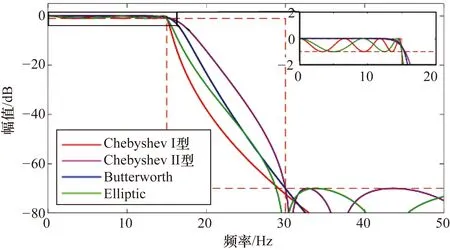
图4 4种不同的IIR数字滤波器的幅频特性曲线
对于FIR滤波而言,则需要考虑窗函数使用的类型,主要考虑阻带衰减指标,同时考虑窗函数的特性。凯塞窗是一种灵活的窗函数,它可以通过调节β值来灵活调整窗函数的旁瓣衰减和主瓣宽度,从而调节滤波器的阻带最小衰减值[25]。同时,使用凯塞窗设计的滤波器与其他常用窗函数设计的滤波器相比,通带波纹较小,对通带信号影响较小。因此,使用凯塞窗设计FIR滤波器较为合适。
但是由于在此参数下设计的IIR和FIR滤波器阶数均较高,若直接将信号通过上述设计好的滤波器进行滤波会产生一定的相位延迟。同时,滤波后的信号输出前端存在自适应的过程,会产生振铃噪声,如图5中绿色波形所示。
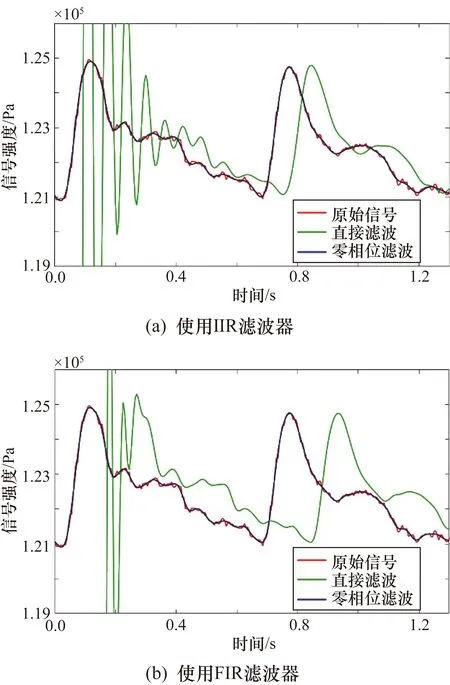
图5 寸部信号使用不同数字滤波器在不同滤波方法下的对比图
对于此种情况的处理,常用的处理方法是对滤波后的信号增加信号修正环节,分别对相位延迟和自适应振铃噪声进行处理。为消除相位延迟,FIR滤波器可以在计算滤波器的群时延后将信号前移以消除时延;非线性相位的IIR滤波器可以通过在滤波器后接全通滤波器来消除时延。为消除自适应振铃噪声,采用在原始数据前延拓产生部分数据,滤波后再去除延拓数据的方式。但是以上处理方式仍然比较烦琐,需要根据每个信号的实际情况逐个处理,工作量大。
因此,本文对设计好的滤波器改用FRR(Forward Filter-Reverse Filter-Reverse Output)零相位滤波法对脉搏波信号滤波。具体方法为:首先,仍按照上文所述方法设计好IIR和FIR滤波器,然后将原始脉搏波信号从首到末顺序滤波;之后,再将滤波得到的信号逆转,从末到首反向滤波,得到与原始信号顺序相反的信号;最后,逆转信号输出,得到最终的波形。使用此方法只需要设计一个滤波器即可完成滤波和信号修正两个环节,从而大幅减轻了工作量。
使用FRR零相位滤波法对寸部信号进行滤波,滤波后的波形图如图5所示。由此可见,滤波后的信号无相位延迟且无自适应振铃噪声,很好地改善了传统滤波器滤波的缺点。因此,本文对设计好的IIR和FIR滤波器采用FRR零相位滤波法滤波,并讨论滤波器的滤波效果。
2.3 小波阈值滤波器设计
设计小波阈值滤波器的过程中,小波分解和阈值处理两个步骤往往有许多参数需要确定,确定这些参数是设计小波阈值滤波器的关键。
小波分解中,需要确定小波基的选择与分解层数。对于小波基的选择标准,往往从不同小波的支撑长度、对称性、正则性、与信号波形的相似性等方面考虑[14]。对于分解层数的选择,则根据各个频段的范围与实际要求,结合奈奎斯特采样定理确定。分解层数越多,噪声和信号的分离程度越明显,但是信号重构后的失真程度也越严重[14]。
分解层数中各个频段的分解范围下限值fn为
(7)
式中:Fs为信号的采样频率。
由于采集到的脉搏波信号为离散信号,因此小波基必须满足可以进行离散小波变换的条件,并综合小波基的对称性、支撑长度、相似性等方面,采用Coiflets系列小波基的coif3、coif4、coif5和Symlets系列小波基的sym4、sym6、sym8。分解层数根据脉搏波信号的频域特性,选择分解层数为4层。
阈值处理中,需要选取阈值和阈值函数,从而抑制含噪信号的小波系数。阈值主要有4种选择:固定阈值(sqtwolog)、无偏似然估计阈值(rigrsure)、极大极小阈值(minimaxi)和启发式阈值(heursure)。sqtwolog阈值和heursure阈值去噪效果相对另外两种阈值更彻底,但是也可能会把有用的信号去除。阈值函数有硬阈值(Hard Threshold)和软阈值(Soft Threshold)两种阈值函数。硬阈值对信号的细节信息保留得较为完整,但也存在部分噪声残留;软阈值处理的信号较为平滑,也使得部分细节信号丢失[18]。
此步骤的参数一般难以直接确定,因此本文阈值选取上述的全部阈值,即固定阈值、无偏似然估计阈值、极大极小阈值和启发式阈值,选取硬阈值和软阈值2种阈值函数,结合选取的几种小波基,对比多种小波阈值滤波去噪方法的效果,以及其中的最佳去噪方法。
2.4 去除基线漂移
拟合基线法更适合于去除脉搏波基线漂移。其中,三次样条插值法拟合曲线是使用较广泛的方法,其可以保证曲线节点处的光滑特性。简单来说,其插值原理为对离散的点使用满足三次插值条件的函数进行拟合,从而得到拟合曲线。
使用三次样条插值拟曲线去除基线漂移的具体方案如下:首先,进行插值以拟合基线。三次样条插值法拟合曲线的关键步骤是要确定好拟合的基准点[26]。使用已去除高频噪声的信号作为去除基线漂移信号,以便于基准点的识别。采用脉搏波信号周期的起始点和结束点作为基准点,拟合插入的点的个数与采样频率相匹配,从而保证曲线精度。拟合基线后,将拟合得到的基线与原始信号相减,即可将基线漂移去除。
3 实验结果与分析
3.1 去除高频噪声效果
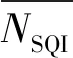
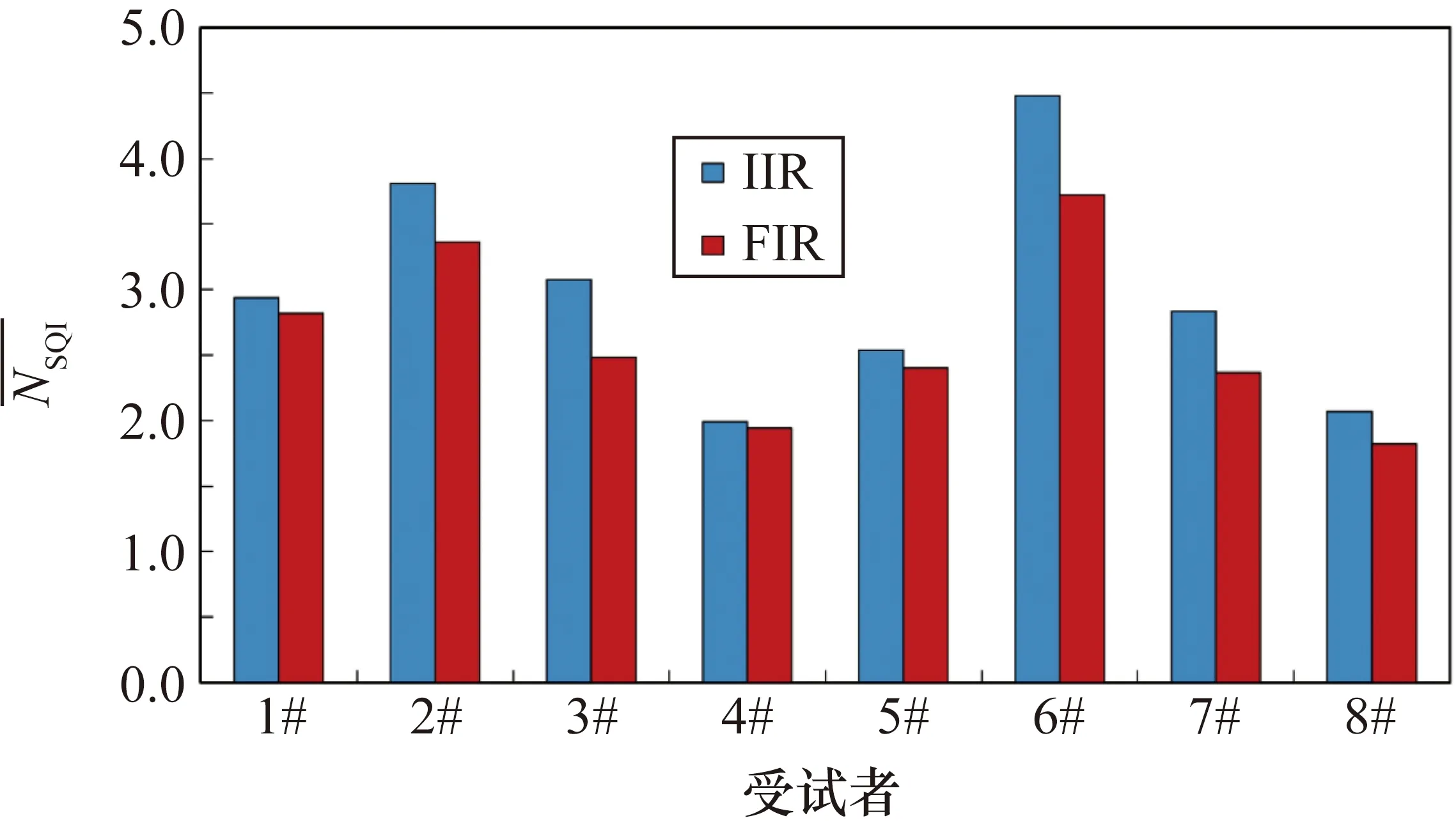
图6 使用IIR和FIR数字滤波器进行滤波的效果对比图
在同一要求下设计滤波器, FIR滤波器的阶数往往比IIR滤波器要高,造成了过大的相位延迟。通过仔细对比2个滤波器的波形可知,FIR滤波器对细节的处理与IIR滤波器相比也有所欠佳,但是整体差异不大,与使用NSQI评估滤波效果的结果相同,证明了NSQI参数评估的准确性。
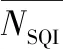
表2 8位受试者均值排名前5的处理方式

表3 配对t检验、效应量指标分析结果
图均值排名前五的小波阈值去噪方法效果对比图
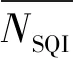
使用最佳滤波方式滤波,滤波前后的脉搏波信号如图8所示。从图8中可以看出,寸、关、尺三部的原始脉搏波信号的高频噪声已很好地去除,滤波后的信号无毛刺、光滑,同时特征点也被保留。
图8 滤波前后的寸、关、尺三部脉搏波信号
3.2 去除基线漂移效果
使用三次样条插值拟合曲线对滤波后的信号去除基线漂移,去除寸部基线漂移的效果如图9所示。去除基线前的原始信号存在一定的基线漂移,去除后所有脉搏波信号周期的起始点和结束点都在同一条水平线上,去除基线漂移效果较好。
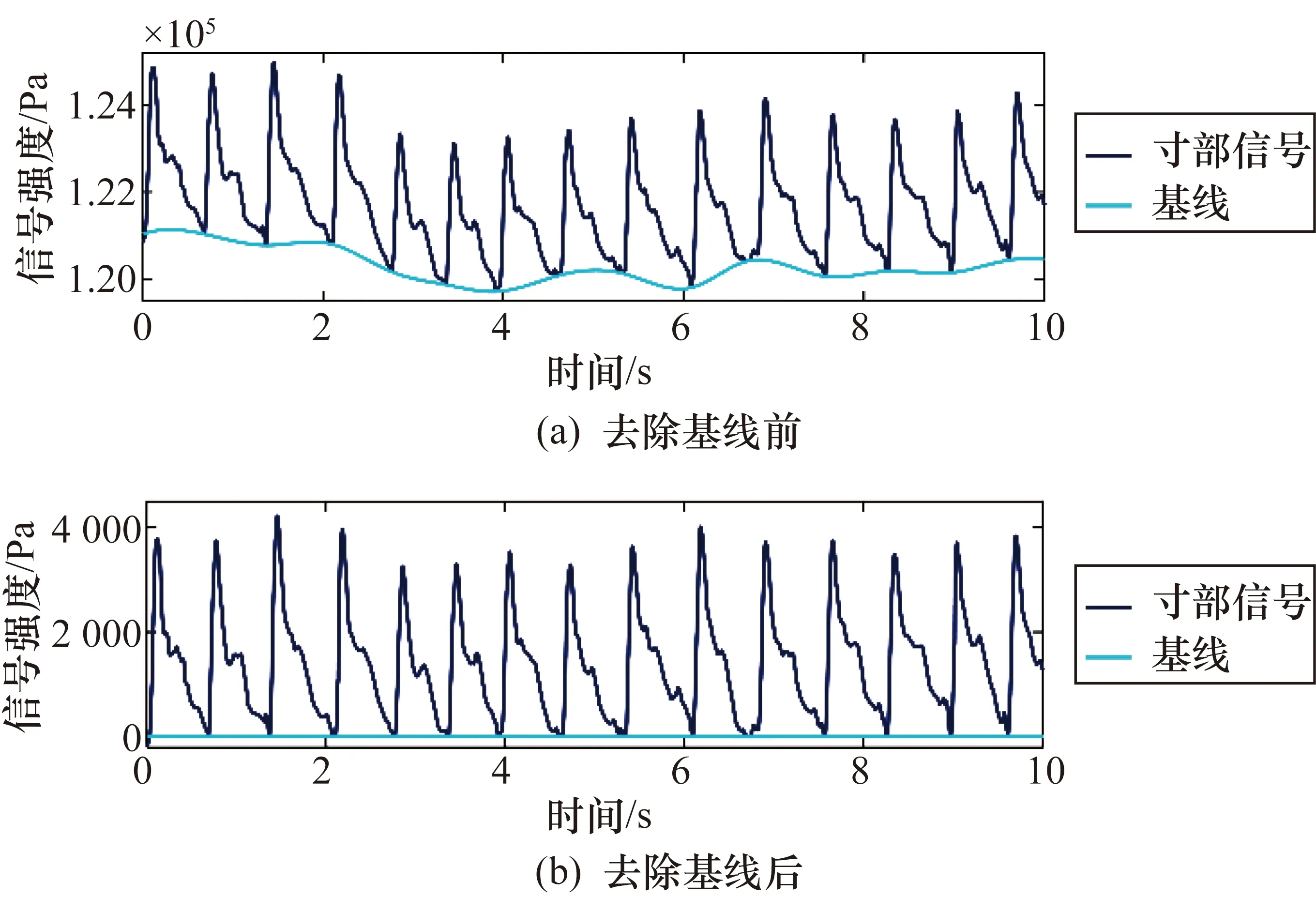
图9 去除基线漂移前后的寸部脉搏波信号
三部脉搏波信号经过预处理的最终结果如图10所示。经过预处理后,脉搏波波形光滑,基线漂移也全部去除,三部脉搏波信号在同一条水平线上。
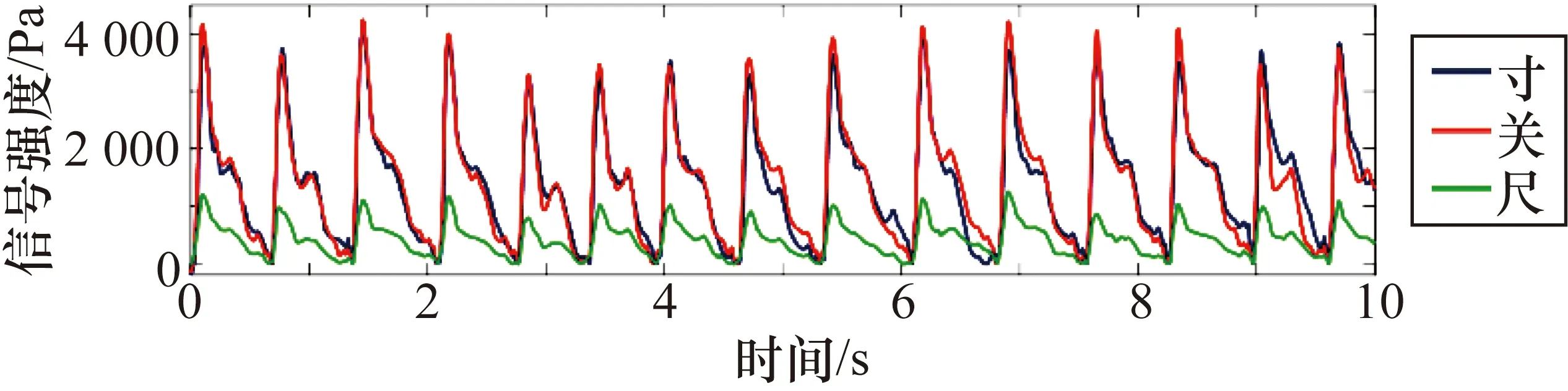
图10 经过预处理后的寸、关、尺三部脉搏波信号
4 结束语
本文针对脉诊客观化中对脉搏波信号预处理的问题进行了探讨。给出了预处理中的基本流程以及其中相关参数确定的方法,使用FRR零相位滤波法改善了传统数字滤波器直接处理脉搏波信号的输出失真问题,建立了对滤波效果的评价参数NSQI,为实际测量中此类无参照信号的评价提供了一定的思路。
对于去除高频噪声的方法,结果表明,使用sym4小波基、sqtwolog阈值、软阈值函数的小波阈值去噪方式效果最好。对于脉搏波信号的基线漂移去除,使用三次样条插值拟合曲线的方式更为合适。将上述2种方法相结合,可以很好地完成脉搏波信号的预处理。
脉搏波信号预处理是脉诊客观化的重要环节,预处理后的信号可以用于通过识别特征点和结合机器学习的相关理论进行智能脉诊,也可以建模计算出血液流速、血压等相关的血液动力学参数,该方法可应用在中西医结合诊断、智慧医疗、健康监测领域。

