深度学习视角下孤电子对数计算方法的建构

赵旭东

(云南省巍山县第二中学)

一、问题提出

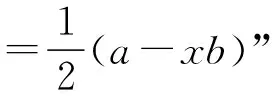
二、中心原子孤电子对数计算的深度学习

(一)辩证看待孤电子对数计算公式的优点和缺陷

(二)理解公式的化学意义、原理,迁移扩展

1.不会确定HCN、CH2O分子中孤电子对数的原因分析

学生不会确定HCN、CH2O分子中孤电子对数的原因,表象:公式用不上;深层次的原因:不理解公式的化学意义、原理;更深层的原因:缺乏深度学习的意识、没有发生深度学习。

2.孤电子对数计算公式的化学意义和原理

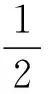
“a”:A的价层电子数;

“x”:与A成键的B有x个;

“b”:B用掉的A的价层电子数(B达稳定结构还需要的电子数,A用自己的价层电子无条件满足);

“-”:减去。

此公式立足于与中心原子A成键的B原子达稳定结构还需多少个电子,这些电子都由A给出,遇到以下两种情况就会出问题:万一A没有那么多价层电子,就会出现负值;如果B不仅与A成键,还与其他原子成键,仍然按与B成键的电子只来源于A处理,那么用此公式计算与客观事实不符。

3.孤电子对数计算公式的迁移扩展

怎样迁移扩展呢?先从教材入手。

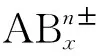
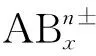
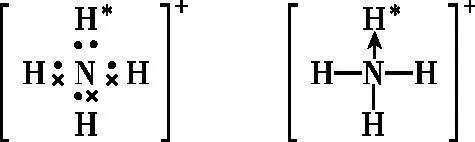
图1

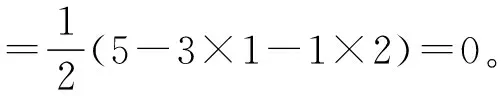
综上,形成离子时失去(得到)的电子,既可以看成中心原子失去(得到),也可以看成该离子中某一个原子失去(得到)。

以上分析,最有价值的是利用成键时中心原子价层电子的使用情况确定孤电子对数,这为孤电子对数计算方法的扩展提供了借鉴。由此推测,只要清楚非ABx型分子中心原子成键时用掉的电子数,就能计算出未参与成键的电子对,进而就能计算出孤电子对数。

(2)CyABx型分子中心原子孤电子对数计算原理及公式

对于ABx型分子,利用乘法原理进行逆向思维,将公式中“xb”换成加法,见图2。

图2

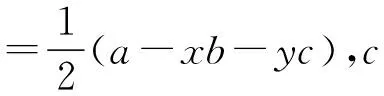
(3)多中心原子的分子(离子),各中心分别计算

(4)用取代观点,化繁为简

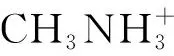
(5)巧记代表性和特殊性物质,用好类比推理

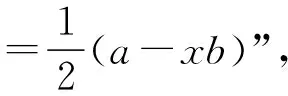
图3

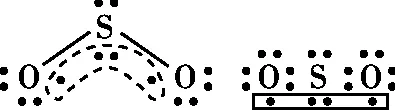
图4

三、启示

本文利用深度学习,从成键时各原子价层电子的使用情况,厘清中心原子孤电子对数的计算原理,促使学生建构新的计算方法。建构这些计算方法,不仅需要付出时间,还需要付出精力,是否值得让学生去做?从高考考查的必备知识、关键能力、学科素养来看,值得去做也必须去做。只有在学习过程中“究其所以然”,即深度学习,才能适应高考的要求。学生在深度学习中,获得的思维能力的提升是死记硬背、机械刷题永远不可能达到的。深度学习能让学生体验到成功的喜悦,这份喜悦又能作用于深度学习,从而形成良性循环。站在立德树人的高度上,教师必须促成学生深度学习。