列生成算法的改进策略研究

罗凤娥，张 鑫，赵 强，杨思瀚

（中国民用航空飞行学院空中交通管理学院，广汉 618307）

0 引言

列生成算法是一种用于解决大规模线性规划问题的迭代算法。该算法的核心思想是通过逐步添加列来构建松弛问题的最优解，从而逼近原问题的最优解。在算法的初期阶段，只考虑少量的变量和约束条件，随着计算的进行，逐渐添加新的变量和约束条件，直到得到原问题的最优解。在每次迭代中，它解决了一个受限的主问题（restricted master problem，RMP）和一个定价问题（pricing issues，PP）。受限的主问题是原始线性规划（linear programming，LP），被限制在其变量的子集中，并由原始线性规划求解器求解，例如原始单纯形算法。与传统的线性规划算法相比，列生成算法在处理大规模问题时具有更高的效率和精度，尤其适用于包含大量稀疏约束条件的问题。此外，该算法还具有较好的可扩展性和灵活性，可以通过调整算法参数和优化策略来满足不同的求解需求。

1 列生成算法的基本原理

列生成算法通过求解子问题（sub problem，SP）来找到可以进基的非基变量，该非基变量在模型中并没有显性地写出来［1］（可以看成是生成了一个变量，每个变量其实等价于一列，所以该方法被称为列生成算法）。如果找不到一个可以进基的非基变量，那么就意味着所有的非基变量的检验数（reduced cost，RC）都满足最优解的条件，也就是说，该线性规划的最优解已被找到。其思路如下：

（1）先把原问题（master problem，MP）转换到一个规模更小（即变量数比原问题少）的问题上，这个只使用部分变量的模型被称为原问题的RMP 问题。在RMP 上用单纯形法求最优解，注意此时求得的最优解只是RMP 上的，并不是MP的最优解。

（2）然后需要通过一个子问题去检测在那些未被考虑的变量中是否有使得RC 小于零的情况，如果有，那么就把这个变量的相关系数列加入到RMP 的系数矩阵中，返回第一步。经过反复迭代，直到子问题中的RC 都大于等于零，此时就找到了MP的最优解。流程如图1所示。

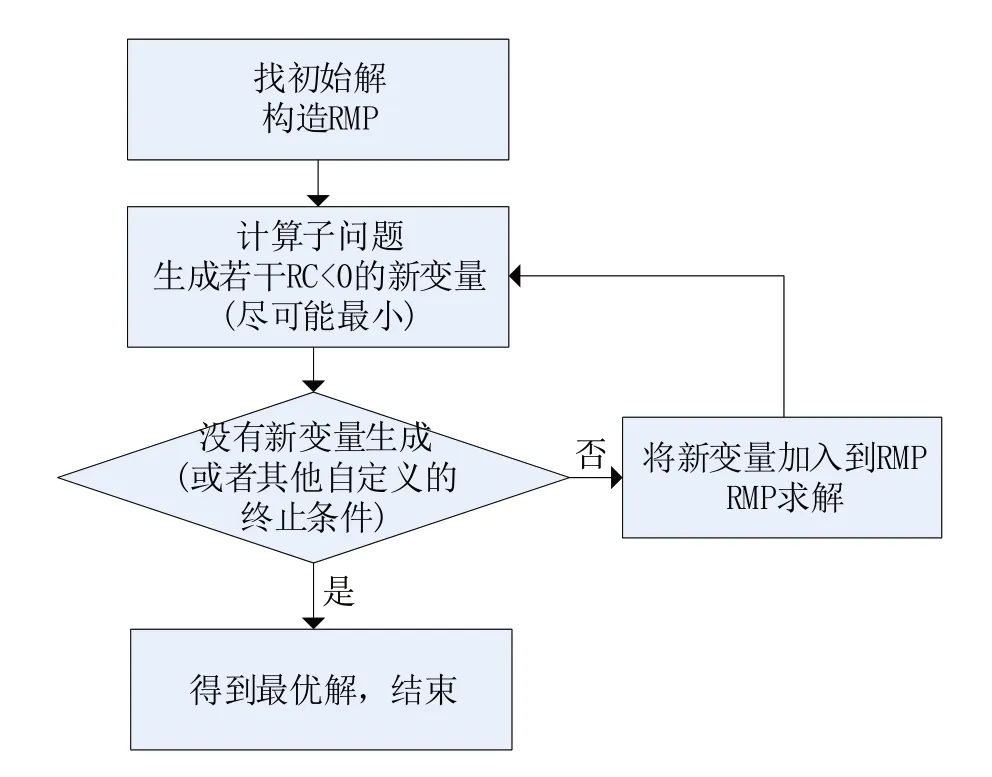
图1 列生成算法流程

2 列生成算法的改进思路

列生成算法的改进思路主要有以下四个方面。

2.1 加速松弛问题的求解

松弛问题的求解是列生成算法中的瓶颈，因此加速松弛问题的求解可以提高整个算法的效率。可以通过优化线性规划求解器、改进算法的分支策略和剪枝技术、引入启发式算法等方法来加速松弛问题的求解。

优点：通过优化线性规划求解器、改进算法的分支策略和剪枝技术、引入启发式算法等方法来加速松弛问题的求解，可以大幅提高算法的效率和精度。

缺点：一些优化方法可能会增加算法的复杂度，导致运算时间和空间开销增加。

2.2 改进列选择策略

列选择策略是列生成算法中的关键因素，决定了列的质量和数量，因此改进列选择策略可以提高算法的精度和效率。可以通过引入先进的列选择策略、基于贪心策略的启发式算法等方法来改进列选择策略［2］。

优点：通过引入先进的列选择策略、基于贪心策略的启发式算法等方法来改进列选择策略，可以提高算法的精度和效率。

缺点：列选择策略的改进需要对问题本身有深入的理解和分析，可能需要大量的实验和测试，才能找到合适的列选择策略。

2.3 优化列集合的管理

列集合是列生成算法中的关键数据结构，对算法的效率和精度有着重要的影响。可以通过优化列集合的更新策略、管理策略、排序策略等方法来提高算法的效率和精度。

优点：通过优化列集合的更新策略、管理策略、排序策略等方法来提高算法的效率和精度，可以改善列生成算法的求解速度和质量。

缺点：列集合管理的优化可能会增加算法的复杂度，导致运算时间和空间开销增加。并且需要仔细选择优化策略，以避免出现不稳定的情况。

2.4 结合其他方法

列生成算法可以结合其他方法来进一步提高算法的效率和精度，如将列生成算法与分支定界算法、混合整数规划算法、模拟退火算法等方法相结合，可以得到更加高效和精确的求解方法。

优点：通过结合其他方法，如将列生成算法与分支定界算法、混合整数规划算法、模拟退火算法等方法相结合，可以得到更加高效和精确的求解方法。

缺点：不同方法的组合需要进行合适的调整和实验，才能找到最优的求解策略。而且，不同方法的结合可能会导致算法的复杂度增加，导致运算时间和空间开销增加。

总体来说，不同的思路和方法在不同的问题和情况下具有不同的优缺点。为了提高算法的效率和精度，需要根据具体问题的特点和求解需求来选择合适的改进方法，并对改进方法进行适当的组合和调整，同时进行大量的实验和测试，以验证改进方法的有效性和性能。

3 基于机器学习的列生成算法改进策略

在用列生成求解时，一些大规模模型容易出现高度简并，导致收敛速度较慢。对于这些问题，可以在每次迭代中生成许多列并添加到受限的主问题中。然而，这样做只会增加处理简并的难度，从而产生反效果。在过去的几年里，研究人员对使用机器学习算法来解决组合优化问题或加速现有的优化方法越来越感兴趣。Bengio等［3］对组合优化的机器学习技术进行了很好的概述。

3.1 列生成算法的基本模型

在每次列生成迭代中，优化受限的主问题并求解定价问题后，得到一组列β。目标是选择要添加到受限的主问题的列βs⊆β的子集。这种列的选择可以被认为是一个二元分类问题，其中我们尝试将每个生成的列分为两个类y∈{ 0,1} ，即如果要选择列，则为1；否则为0。设l为列生成迭代号，αl为迭代开始时受限的主问题中出现的列集l，βl为此迭代中生成的列。对于每一列p∈βl，我们定义了一个决策变量yp，如果选择列p则取值1；否则取0。由此得到用于列分类任务的混合整数线性规划模型如下：

其中：p是变量θp的指数集；cp∈R,ap∈Rm分别为θp的代价系数向量和约束系数向量；b∈Rm是约束条件（2）的右边向量。注：这些约束条件中的一些或全部也可以是不等式。如果没有yp变量和约束（4）和（5），模型（1）～（5）将恰好是迭代l+ 1 时的受限的主问题。假设足够小，这些变量和约束只考虑最小化所选列的集合。这些列对应于yp= 1的列，即yp列与正值θp变量相关（约束（8））。因此，迭代l时受限的主问题中要添加的列子集为

3.2 图神经网络概述

图神经网络（GNNs）为图结构化数据的学习提供了一个有效的框架。它们可以用于节点分类、链接预测、图预测、文档分类甚至组合优化等任务。它们最初由Gori 等［4］提出，并由Scarselli 等［5］进一步发展。GNN 的目标是以迭代的方式聚合来自邻居节点的信息来学习节点表示。然后，使用节点表示形式为节点分类任务生成输出标签。

GNN 概述：给定一个图G=(V,E)，其中V是节点的集合，E是边的集合，每个节点v∈V由其特征向量xv来表示。目标是通过聚合来自邻居节点的信息，迭代地更新节点的表示。设h(k)v是节点v∈V在迭代k处的表示向量k=0,1,…,K。设N(v)为v∈V作为相邻节点集合，如图2 所示，通过聚合邻居节点的表示来迭代更新表示向量。在迭代k＞0 时，该聚合函数（aggr）首先用于计算每个节点v∈V的聚合信息向量a(k)v:

图2 图神经网络

h(v0)=xv,∅(k)是一个学习函数。函数aggr对于节点顺序的排列应该是不变的。然后，使用一个表示comb的函数，我们将聚合的信息与给定节点的当前状态结合起来，以获得更新的节点表示向量:

其中φ(k)是另一个学习函数。

随着迭代的进行，节点从较远的节点收集信息。在最后的迭代K中，节点v∈V的表示h(K)v可以用来预测它的标签，记为fv，通过应用最终习得的变换，记为out，即:

学习的函数∅(k)，φ(k)，out通过使用多层感知器前馈神经网络实现。

3.3 算法模型

上述内容中存在明显的架构是用一个节点表示每一列，如果两个节点对应的列至少有一个共同的约束，就用一条边连接它们。但是，在这种情况下，边的数量会非常大，模型中很难包含对偶值信息。另一种架构使用具有两种节点类型的二部图：列节点V和约束节点C。如果列v对约束c有贡献，则在节点v∈V和节点c∈C之间存在边(v,c)。这种表示的优点是可以将特征向量附加到约束节点上，这将允许我们轻松地包含双重信息。

因为有两种节点类型，所以每次迭代都分两个阶段进行，且在一次迭代之后，每个列节点都包含一些关于对相同约束有贡献的其他列的信息。然而，通过执行额外的迭代可以传递更好的信息。

列表示h(vK),v∈V，然后用于预测标签yv∈{ 0,1} 。以下为算法示例：

4 结语

本文通过对列生成算法进行探索，针对列生成算法求解子问题的速度，进行相应的分析研究并提出对应的改进策略，同时通过相应的实验验证了本文提出内容的可行性。本文提出的改进策略对于提高列生成算法的计算速度具有很大的增益，也为各个应用领域运用列生成算法提供了一些改进思路。