基于蒙特卡洛法与GUM评定测量不确定度的对比分析

黄 钰，廖芳芳，付 玉，赵 豆，闫晓钰 礼 莹，罗玉珺，王建宇

（中国核动力研究设计院，成都 610213）

0 引言

在核电厂现场，仪器仪表产生的大量数据需要进行采集、处理、分析和记录，如何保证这些数据的准确性和可靠性对核电厂的安全运行和质量管理都至关重要[1]。HAD 102/14《核电厂安全相关仪表和控制系统》中明确规定，对仪器仪表必须考虑其不确定性条件下的运行状态，使设计限制符合安全标准[2]。在检测和校准过程中，测量不确定度是表征合理地赋予被测量之值的分散性，是与测量结果相关联的参数[3]，是评定测量水平的技术指标，是判定测量结果质量的重要依据，是保证量值准确、可靠传递的有效手段。对仪控专业来说，需要准确计算核电厂仪器仪表的测量不确定度，设定安全合理的整定值[4,5]，以保障核电系统的稳定有效运行[6]。

近年来，测量不确定度的评定普遍采用GUM 法。该方法采用线性化模型评定不确定度，要求输入量的概率分布具有对称性，测量模型可用线性化表示且易求偏导数等条件限制[7]，使评定结果易产生偏差。MCM 采用大量样本进行概率密度传播[8]的方式，可以有效弥补GUM 的缺陷和不足，而现代科技的发展推动了数字化进程，使蒙特卡洛法能在仪器仪表检测校准领域更广泛有效地应用。本文结合已广泛用于核电厂中的压力表，采用GUM 和MCM 两种测量不确定度评定方法对其测量误差不确定度进行评定与对比分析，并利用MCM 验证GUM 评定结果的准确性和可靠性。

1 仪表基本信息

某核电厂氢气供应系统（GRV），系统正常运行期间压力为0.3MPa，所用压力表作为一次测量元件，对其进行不确定度分析与评定。标准器和被检表参数见表1。

表1 标准器和被检表参数表Table 1 Parameter list of measurement standard and measurement object

1.1 检定前准备工作

根据JJG52-2013《弹性元件式一般压力表/压力真空表和真空表》对标准器和被检压力表进行外观和结构检查，应当符合通用技术要求[9]。检定温度（20±5）℃，相对湿度≤85%，环境压力符合大气压力。

1.2 检定方法

采用0.02 级活塞式压力计对1.0 级一般压力表进行检定。活塞式压力计是基于作用在活塞下端面流体压力所形成的力，与施加于活塞上端面砝码以及活塞自身所产生的重力F 相平衡的流体静力学原理。当整个系统平衡时，读取被检压力表的示值。该示值与活塞压力计加砝码产生的压力值之差，即为被检压力表的示值误差。

1.3 测量模型

一般压力表的测量误差数学模型：

式（1）中：

ΔP——被检测表的示值误差（MPa）。

P测——被检测表的显示值（MPa）。

P标——活塞式压力计的标准值（MPa）。

2 蒙特卡洛测量不确定度评定与表示（MCM）

蒙特卡洛方法（MCM）是利用测量模型进行传播，通过输入量的概率密度函数计算出输出量的概率密度函数，利用现代仿真技术对输入量进行随机离散抽样，再根据函数模型得到输出量的样本值。根据输出量的离散分布得到最佳估计值、标准不确定度和选定概率下的包含区间，适用于多个输入量对应单个输出量的测量模型[10,11]。

MCM 蒙特卡洛评定测量不确定度的步骤如下：

1）建立模型，分析不确定度来源

测量不确定度是经过分析和评定得到的说明测量结果分散性的参数。使用活塞式压力计对压力表进行测量时，其测量不确定度来源可从测量仪器、测量环境、测量方法以及测量人员等方面进行分析。应尽量减少操作过程中引入不确定度，及时对检定中的数据进行分析，避免产生不必要的误差。本文从图1 所示几方面，对一般压力表的测量不确定度的来源进行分析与评定。

图1 不确定度分量Fig.1 Components of uncertainty

可以将误差数学模型式（1）表示为：

2）确定输入量Xi的分布类型及概率密度函数（PDF）g（X）

① 重复测量的概率密度函数

测量重复性导致的测量不确定度中，包含了测量时各种随机影响的贡献。如果其中包含由于分辨力不足引起的测得值的变化，这种情况下只要评定测量重复性导致的不确定度，就不必再重复评定分辨力导致的不确定度。

选取0.3MPa 校准点为例，通过连续测量获得测量列，见表2。

表2 0.3MPa点的测量数据Table 2 Measurement data of 0.3MPa

平均值为：

标准不确定度：

根据最大信息熵原理，重复测量服从正态分布。

② 示值估读的概率密度函数

按照一般压力表检定规程，估读时要求读到分度值的1/5，因此估读的不可靠性以1/5 分度值估计。该表的最小分度值0.02MPa，则估读误差下限a 为-0.004MPa，估读误差上限b 为0.004MPa。根据最大熵原理，估读误差服从均匀分布。

③ 数值修约的概率密度函数

按照一般压力表检定规程，修约要求到被检表最小分度值的1/5，修约误差为估读误差的1/2，则修约误差下限a 为-0.002MPa，修约误差上限b 为0.002MPa。根据最大熵原理，服从均匀分布。

④ 环境温度变化的概率密度函数

温度变化对被检表的稳定性会产生一定影响，实验室保持在（20±5）℃的温度条件下，一般压力表的弹性元件膨胀系数为k=0.0004/℃，Δt=±5℃，a=kpΔt。温度的变化下限a 为0℃，上限b 为5℃。根据最大熵原理，服从均匀分布。

⑤ 活塞压力计准确度的概率密度函数

选用的活塞式压力计根据校准证书，准确度等级为0.02 级，在0.3MPa 点的最大允许误差为±0.00006MPa，在该点下限a 为0.29994MPa，上限b 为0.30006MPa。根据最大熵原理，服从均匀分布。

⑥ 活塞压力计工作面与一般压力表指针中心高度差的概率密度函数

根据一般压力表检定规程可知，当实验不可避免地产生静压差时，应当引入修正压力ΔP=ρgΔh，其中变压器油在20℃时的密度为ρ=0.86×103kg/m3，本地重力加速度9.7913m/s2，高度差Δh=0.1m，最大允许误差为±0.2mm。以上可得ΔP的下限a 为0.000840MPa，上限b 为0.000844MPa。因此，高度差根据最大熵原理，服从均匀分布。

3）确定样本量M

抽样次数M 的取值越大结果越准确，但相对地也增加了程序运行时间。M 取值应远大于1/(1-P)，其中p 为包含概率（取值一般为95%或99%），本次仿真M 取106。

4）求出Y 的模型值

运用MATLAB 对输入量的概率密度函数g(X)抽取M个样本值xir，i=1~N，r=1~M，将该数值按严格递增次序排序带入模型y=f(x1r,x2r,...,xNr)，得到Y 的概率密度函数（PDF）的离散表示为G。

5）报告结果

由G 计算出Y 的估计值y

y 的标准不确定度u(y)由标准偏差u(y)表示

由G 计算出Y 的95%包含区间[ylow，yhigh]

Matlab 仿真运行结果：

95%的包含区间的端点：[ylow，yhigh] = [-0.0011,0.0120]

3 测量不确定度的评定方法对比分析

3.1 测量不确定度评定与表示法（GUM）

根据GUM 的定义，该方法是利用线性化模型传播，通过输入量的标准不确定度来确定输出量的标准不确定度，通过置信区间来表征输入量和输出量之间的关系。

由第2 节分析可计算出不确定度分量的标准不确定度见表3。

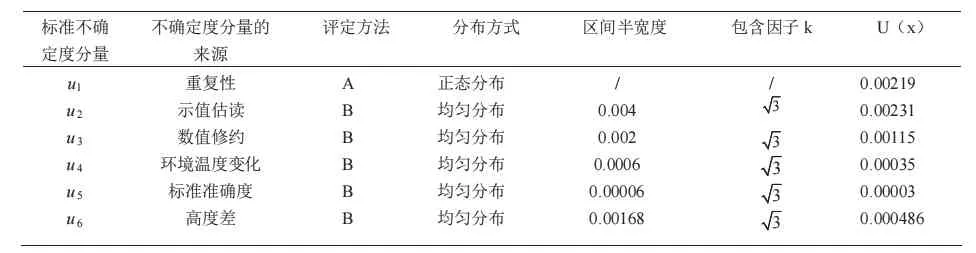
表3 不确定度分量明细表Table 3 List of standard uncertainty components

由一般压力表的测量数学模型可知，其测量误差包括被检表产生的不确定度U测和测量标准产生的不确定度U标，并且这两个不确定度分量互不相关。灵敏度系数为：

将6 个不确定度分量进行合成，得到测量误差的合成标准不确定度：

扩展不确定度，按置信概率95%估计，取k=2。

3.2 采用蒙特卡洛法验证GUM的过程与结果分析

目前，GUM 法在不确定度评定的大多数场合仍然适用，但是其应用条件不易满足，所以在JJF1059.2-2012《蒙特卡洛测量不确定度评定与表示》中建议采用GUM 和MCM两种方法对不确定度进行评定，并将结果进行比较验证，最终采用比较结果较好的方法进行不确定度的评定。

由3.1 节GUM 可得在约定的95%包含区间的左右端点值为：

由3.2 节MCM 可得约定的95%包含区间的左右端点值为：

由标准不确定度u(y)=0.0034=34×10-4，l=-4，确定数值容差：

对GUM 和MCM 获得的相同包含区间进行比较，即比较两个包含区间的各自端点的绝对偏差与数值容差的大小。若小于δ，则GUM 法通过验证。反之，则GUM 法未通过验证。

由结果可知，dlow和dhigh均大于δ，GUM 法未通过MCM验证。表明GUM 法在对压力表测量误差的不确定度评定中存在一些问题。由表4 和图2（曲线为GUM 法的概率密度曲线，直方图为MCM 法的概率密度分布情况）可以看出，GUM 的最佳估计值发生偏移，从而导致包含区间产生一定的偏移。GUM 在95%的包含区间大于MCM，GUM 的评定结果较为保守，MCM 的评定结果较为精确。

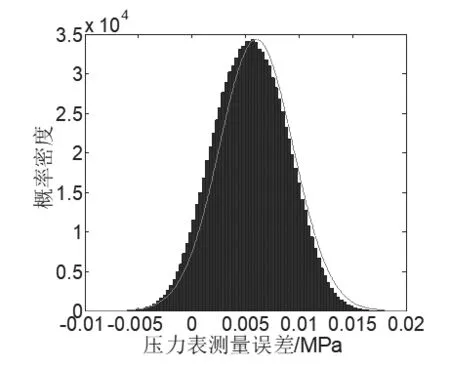
图2 GUM和MCM概率分布Fig.2 Probability distribution of GUM and MCM

表4 GUM与MCM评定结果Table 4 The evaluation results of GUM and MCM

4 结束语

在对核电厂仪器仪表进行质量控制时，测量不确定度是评定测量结果质量的一个重要指标。本文重点研究了蒙特卡洛法在测量不确定度评定中的应用，并以核电厂氢气供应系统中使用的压力表为例，详细对其运用MCM 法和GUM 法进行不确定度的来源分析、过程评定和结果分析，并采用MCM 法对GUM 法的评定结果进行验证。结果表明，传统的GUM 法是对线性化模型的不确定度进行传递，在实际测量模型中做出一些假设和近似，使得对压力表测量误差输出量的概率分布会产生偏差，造成评定结果不够精确，较为保守，从而造成整定值的计算也较为保守，对经济效益造成一定的影响。而MCM 是对输入量的概率密度进行传递，不受分布区间的影响，比GUM 适用范围广。同时，由于现代数字化技术的进步，使得MCM 可以采用模拟仿真大量数据样本进行统计分析与计算，克服了GUM 人工计算存在的缺点，缩短了计算时间，可靠程度更高。