电磁感应中双杆模型归类探究
李宁宁 刘立毅
(山东省德州市第一中学)
两根平行导轨置于水平面或斜面上,处于垂直导轨平面的匀强磁场中,两个金属杆垂直放在导轨上切割磁感线,我们称此类问题为双杆问题。下面将此类问题的三种模型进行归纳总结,供参考。
一、导轨等间距,一杆有初速度
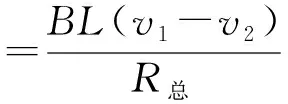
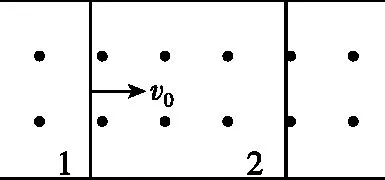
图1
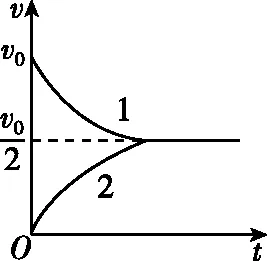
图2
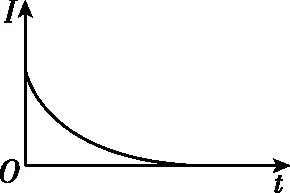
图3
【例1】(2022·辽宁卷·15)如图4所示,两平行光滑长直金属导轨水平放置,间距为L,abcd区域有匀强磁场,磁感应强度大小为B,方向竖直向上。初始时刻,磁场外的细金属杆M以初速度v0向右运动,磁场内的细金属杆N处于静止状态。两金属杆与导轨接触良好且运动过程中始终与导轨垂直。两杆的质量均为m,在导轨间的电阻均为R,感应电流产生的磁场及导轨的电阻忽略不计。
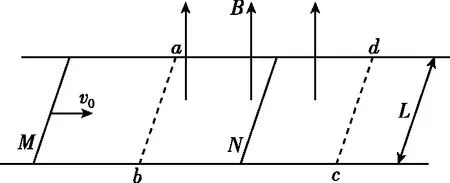
图4
(1)求M刚进入磁场时受到的安培力F的大小和方向;
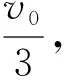
(3)初始时刻,若N到cd的距离与第(2)问初始时刻的相同、到ab的距离为kx(k>1),求M出磁场后不与N相撞条件下k的取值范围。
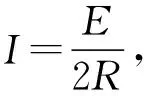
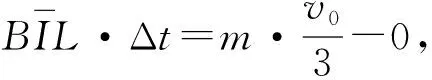
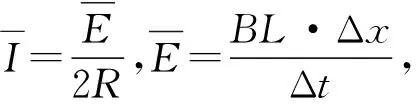
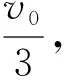
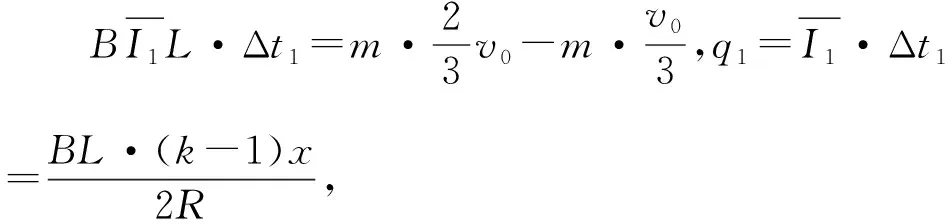
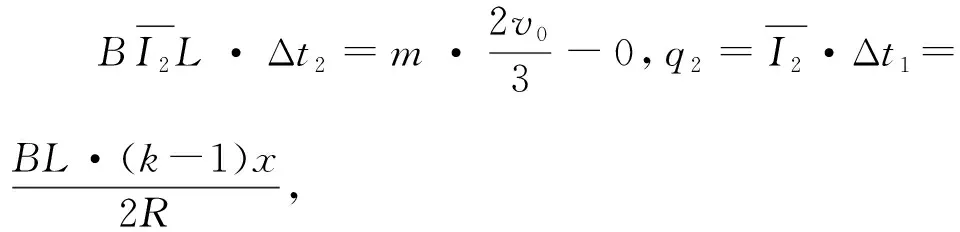
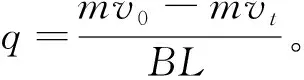
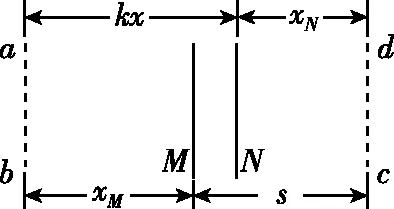
图5
二、导轨等间距 一杆受外力
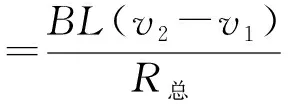
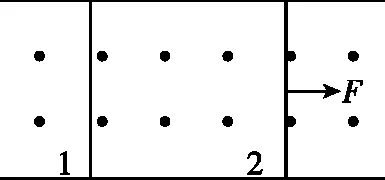
图6
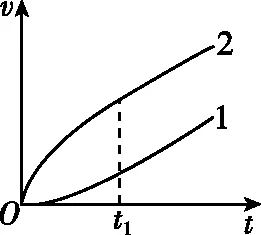
图7
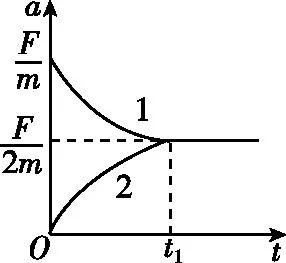
图8
【例2】如图9所示,水平放置的平行粗糙金属导轨间距为L,导轨处在竖直向上、磁感应强度为B的匀强磁场中,两个相同的金属棒ab、cd垂直导轨平行放置,与导轨始终接触良好,每个金属棒质量均为m,接入电路的电阻均为R,两个金属棒与导轨间的动摩擦因数均为μ,重力加速度为g,开始时cd棒锁定在导轨上,对ab棒施加水平向右的恒定拉力F1=3μmg,棒ab前进的距离为d时速度达到最大值,此时将恒力大小变为F2=2μmg,方向不变,同时解除对棒cd的锁定,再经过一段时间金属棒cd做匀速运动。导轨足够长且电阻不计。求:
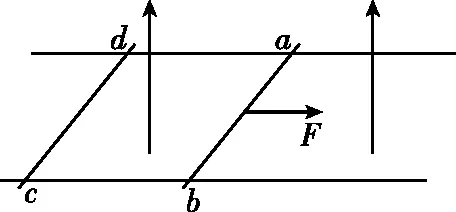
图9
(1)棒ab的最大速度v的大小;
(2)棒ab从开始运动到最大速度的过程中产生的焦耳热Qab和安培力做的功W安;
(3)棒ab和cd匀速运动的速度v1和v2的大小;
(4)棒cd匀速运动后经时间t,回路中产生的焦耳热Q焦2和总热量Q总。
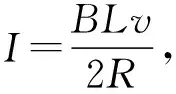
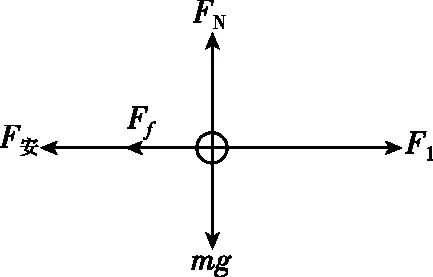
图10
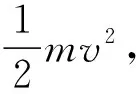
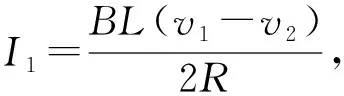
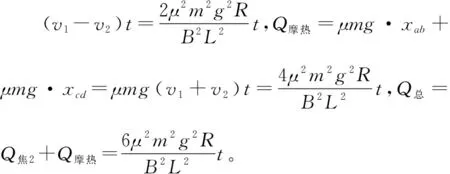
【评析】第(2)问,解题关键是掌握焦耳热公式Q焦=-W安及适用条件:①纯电阻电路;②动生电动势;③单棒为闭合回路的唯一电源,无反电动势;④单棒所受安培力做负功;⑤磁场静止(或以相对磁场静止的物体为参考系计算安培力的功)。本问符合这5个条件,公式可用,即闭合回路的总焦耳热等于安培力对棒ab做功的负值。第(4)问,两棒均为电源,不符合前述5个条件,安培力对任一单棒ab(或cd)做的功W安单≠-Q焦。当两棒都切割磁感线时,电路中的总焦耳热等于一对相互作用的安培力对两棒所做总功的负值,即Q焦=-W安总。因此本题中Q焦=-(W安ab+W安cd)。电流通过导体时产生的热量(电热)叫焦耳热,常用Q焦=-W安、Q焦=I2Rt计算,物体间因滑动摩擦力做功产生的能量叫热能,即内能,俗称摩擦生热,常用Q摩=Ff·Δx计算。两者无必然关系,需注意区分。
三、导轨不等间距 一杆有初速度
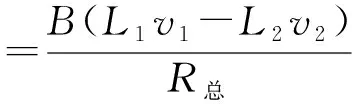
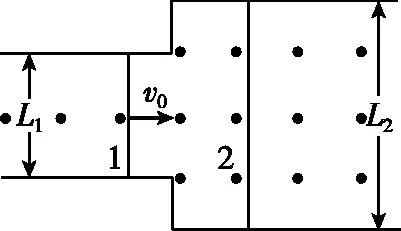
图11
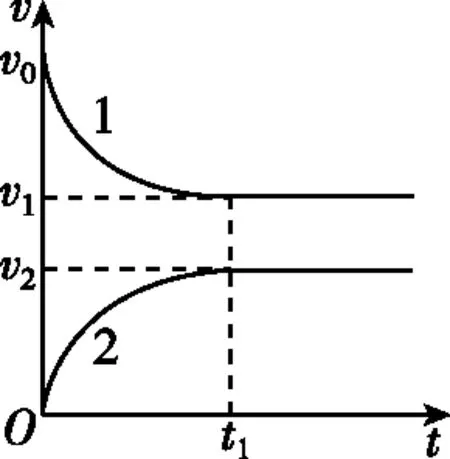
图12
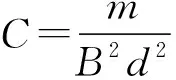
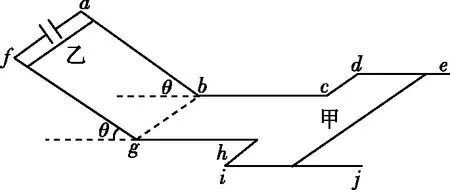
图13
(1)导体棒乙到达bg时的速度v1大小;
(2)导体棒乙在水平导轨上运动的过程中,闭合回路面积的改变量ΔS;
(3)导体棒乙在水平导轨上运动的过程中,导体棒乙上产生的焦耳热Q乙。
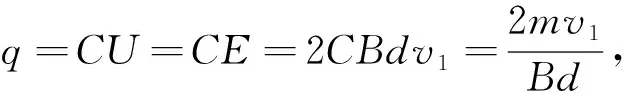
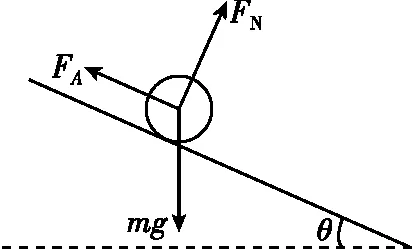
图14
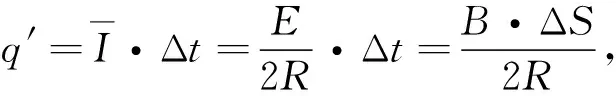

——以2023年高考湖南卷物理第14题为例
——以一道物理竞赛题为例

