用于雷达信号分选的连通k近邻聚类算法

司伟建, 张 悦, 邓志安,*

(1. 哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工程大学先进船舶通信与信息技术工业和信息化部重点实验室, 黑龙江 哈尔滨 150001)

0 引 言

雷达信号分选是无源探测中的关键处理过程,其本质是依据由接收机产生的信号脉冲描述字(pulse descriptor word,PDW)数据与由已有雷达信号先验知识中提取的雷达信号的规律性对雷达信号进行分类的过程。由于现代电子战信号环境中信号形式复杂多样,随着雷达反对抗技术的发展[1-3],传统的基于脉冲重复间隔(pulse repetition interval,PRI)的信号分选方法已无法有效提取雷达信号数据中的信息[4]。如何利用不同雷达之间参数的差异性以及同部雷达信号参数的相关性与规律性对雷达信号进行实时有效的分选,是一个有待深入研究的课题。

聚类分析的目的在于发现密切相关的观测值簇,使得与属于不同簇的观测值相比,属于同一簇的观测值之间尽可能相似[5]。因此,信号分选领域目前的研究热点是聚类信号分选。文献[6]对近年来研究和发展的聚类分选算法进行了综述。目前大多数聚类分选算法有基于原型、基于密度以及基于图的聚类分选算法。

基于原型的聚类,簇由这样的对象组成:簇中任何对象距离该簇的原型比距离其他簇的原型更近[5]。典型的基于原型的聚类有k均值(k-means)聚类[7]与模糊c均值(fuzzycmeans,FCM)聚类[8]。这类算法需要指定聚类数目并随机初始化聚类中心,不适用于未知信号环境中的分选;其次,原型即为簇中心点,因此这类算法适用于球形簇,不适用于参数捷变雷达所形成的矩形簇。后续有众多学者在聚类数目和聚类中心确定等方面进行了研究,分别采用统计直方图[9]、自组织映射(self-organizing feature mapping,SOFM)[10]、主成分分析(principal component analysis,PCA)[11]以及支持向量聚类(support vector clustering,SVC)[12]等方法确定聚类数目与聚类中心,而上述方法均只适用于球形簇。Cao等[13]于2018年提出的基于密度的FCM多中心重聚类算法适用于非凸数据集,同时引入基于快速搜索和发现密度峰值(clustering by fast search and find of density peaks,CFSFDP)算法来生成初始中心点,解决了基于原型聚类算法的两大缺陷,但该算法运算量较大。

基于密度的聚类,簇是对象的稠密区域,被低密度区域所环绕[5]。1996年,Ester等[14]提出经典的基于密度的聚类算法——基于密度的噪声应用空间聚类(density-based spatial clusering of applications with noise,DBSCAN),其具有可发现任意形状簇的优点,但其对于密度变化数据集聚类效果较差,可能造成低密度区域被丢弃或高密度区域被合并为同一簇等问题。DBSCAN需要确定两个参数簇的半径Eps与簇的最少点数MinPts,文献[14]提出了基于k距离图的确定方式,需要人工参与。为自动确定聚类参数,多位学者提出了多种方法,分别采用核密度估计[15-16]、K平均最近邻与数学期望法[17-18]相结合的方法确定聚类参数,实现自动化聚类。2021年,王星等[19]提出了基于云模型的CMDBSCAN算法,其结合距离曲线倾角突变获取Eps参数并根据信号密度分布设置MinPts,同时结合多维云模型对分选结果进行有效性评估,进一步优化参数设置。Chen等[20]引入差分法和反三角函数确定聚类参数,并将其用于聚类分选,提高了算法可靠性和分选精度。

基于图的聚类,将簇定义为图的连通分支[5]。2005年,张兴华[21]提出的模糊聚类算法通过计算各数据点的相似度,将相似度高于阈值的归为一类;实质上是在由数据点构成的图中将相似度高于阈值的数据点连通,而簇为连通的数据点形成的集合,因此其属于基于图的聚类算法,适用于发现任意形状的簇。2008年,贺宏洲等[22]将模糊聚类算法用于雷达信号分选。2009年,刘旭波等[23]提出了熵值法,用于确定聚类中各维参数的权重。2014年,尹亮等[24]提出了基于有效性函数确定最佳聚类的算法,使用Calinski-Harabasz (CH)指标确定最佳阈值完成聚类,但该方法需要多次运行模糊聚类,造成算法复杂度较高。2020年,文献[25]提出了低复杂度模糊聚类算法,降低了时间复杂度与空间复杂度。

本文在模糊聚类算法的基础上,将模糊聚类原有的λ邻域范围搜索变为λ邻域内k近邻搜索。在使用合适的数据结构与搜索算法[26]的情况下,以牺牲空间复杂度(扩大至k倍)为代价将时间复杂度降低(由平方阶降低至线性对数阶),这在计算机技术与存储技术飞速发展的今天是可以接受的。同时,基于k距离图提出了一种新的阈值确定方式,结合刘旭波等[23]提出的熵值法可实现无参数自适应聚类,可在复杂信号环境中进行实时、有效的信号分选。

1 低复杂度模糊聚类算法

1.1 算法原理

文献[25]中提出的低复杂度模糊聚类算法结合文献[23]中提出的熵值法确定参数权重后得到的算法,可表述为算法1。

算法 1 低复杂度模糊聚类算法输入:数据集X,距离阈值λ输出:簇标签1. 对数据集X进行标准化与归一化处理;2. 使用熵值法确定各维参数权重;3. 初始化并查集;4. 依次选取数据集X中两数据点计算距离d,当距离d低于阈值λ时,进行集合归并;5. 查询并查集,分配簇标签并返回。

在低复杂度模糊聚类算法中,数据集X是一个n×m的矩阵,其中每一行均为一个数据点,每个数据点具有m个维度,共n个数据点;距离阈值λ的取值范围为[0,1],距离度量可使用各种Minkowski距离度量,通常使用曼哈顿距离或欧氏距离。对应于聚类雷达信号分选,数据集X即为脉冲描述字向量,每个数据点对应一个信号的脉冲描述字或其子集。

假设有图1所示数据分布的数据集,其中点划线方框所标识的是数据集中的簇,簇以外的数据点即为环境中的噪声点或离群点。

图1 数据分布Fig.1 Data distribution

对于低复杂度模糊聚类算法,其依次计算数据集中两点间距离,距离小于阈值λ时,便将两点连通。如图2所示,数据点a与b之间的距离小于阈值λ,因此将其连通。

图2 距离小于阈值时连通两点Fig.2 Connecting two points when the distance is less than the threshold

聚类结束后,得到的结果如图3所示。簇为图中的连通分支,如簇A、簇B;而对于图2中的噪声点c,由于没有数据点位于其λ邻域内,因此形成单点簇。

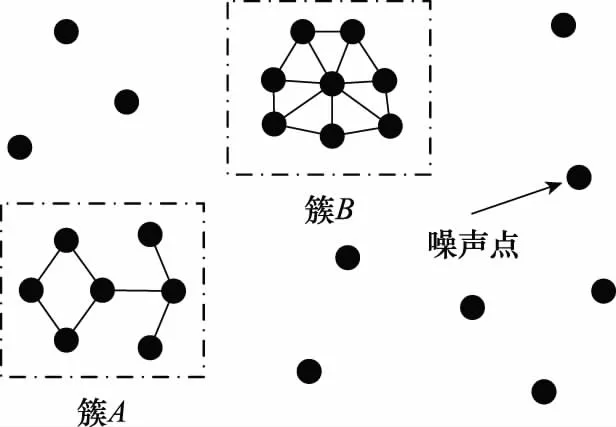
图3 聚类结果Fig.3 Result of clustering

1.2 低复杂度模糊聚类算法存在的问题

低复杂度模糊聚类算法存在如下两点问题:

(1) 由于低复杂度模糊聚类算法需要依次计算数据集中两点间的距离,共需要进行n(n-1)/2次距离计算与并查集归并,具有O(n2)的时间复杂度,对于高脉冲密度的信号环境以及对实时性要求较高的场景,仍无法满足实时性的需求。

(2) 阈值参数的确定基于文献[24]所提出的确定最佳聚类的方法,该方法需依次调整阈值参数λ进行算法1的聚类过程,并计算聚类结果的CH指标,选取CH指标最大值所对应的阈值λ为最佳阈值,导致算法复杂度进一步增加,时间复杂度变为O(l·n2),其中l为算法迭代次数。经过实验,阈值参数的步进会影响聚类参数的确定效果与算法复杂度,进而影响最终聚类效果。

为解决低复杂度模糊聚类算法存在的上述问题,提出了一种连通k近邻聚类算法。

2 连通k近邻聚类算法

2.1 连通k近邻

低复杂度模糊聚类算法也可理解为:对于每个数据点而言,搜索位于其λ邻域内的其他数据点并与其连通,簇为图的连通分支。由于范围搜索具有O(n)的时间复杂度,因此低复杂度模糊聚类算法具有O(n2)的时间复杂度。

为降低其时间复杂度,将范围搜索变为k近邻搜索,即连通每个数据点与其k个近邻,簇为图的连通分支。如图4所示,将数据点a和噪声点d分别与其k近邻连通,此处k=3。

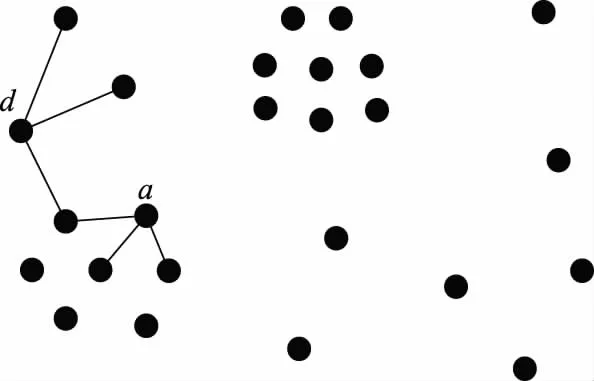
图4 连通数据点与其k近邻Fig.4 Connect the data point to its k nearest neighbors

在使用合适的数据结构(如kd树、bd树)时,k近邻搜索的时间复杂度为O(k·log2n)[26],因此可将算法整体的时间复杂度降低至O(k·n·log2n),log2n为对n取以2为底的对数。

然而如图4所示,仅将范围搜索变为k近邻搜索会导致噪声点d也与其k近邻连通,进而造成将信号环境中的噪声点d与有效数据点a相连通,从而使结果簇中包含了噪声点。在某些特殊的场景中,甚至会将数据集中所有数据点聚为一簇。为解决这一问题,仍引入距离阈值λ,即将数据点与其λ邻域内的k近邻相连通,如图5所示。由于实际场景中噪声点相对稀疏,因此可通过设置合适的距离阈值区分噪声点与有效数据点。

图5 将数据点与位于λ邻域内的k近邻连通Fig.5 Connecting the data point to the k nearest neighbors in the λ neighborhood

2.2 基于k距离图的阈值确定

阈值λ的选取十分重要,其直接影响聚类效果。为清晰地说明聚类效果随阈值λ变化而变化的情况,按表1所列雷达参数生成序列时长为100 ms的雷达信号并混合脉冲流密度为10 000脉冲每秒的噪声构成测试数据集。对测试数据集在不同λ阈值下进行聚类,统计聚类结果的3个指标:簇数量nc(即聚类所得簇数量,不包括噪声点形成的单点簇)、可能存在雷达的簇数量nr(含有10个以上数据点的簇数量)以及平均纯净度pavg(各个簇纯净度的平均值)。其中簇的纯净度定义为簇中主要雷达信号(同一簇中可能存在来自于多部雷达的信号,其中占比较大的雷达信号称为主要雷达信号)所占的比例。

表1 雷达列表

图6为簇数量nc、可能存在雷达的簇数量nr随阈值λ的变化曲线图,图7为平均纯净度pavg随阈值λ的变化曲线图。从图中可看出阈值λ的变化对聚类结果整体上有如下影响。

图6 簇数量nc、nr随阈值λ的变化曲线Fig.6 Change curve of the number of clusters nc andnr with the threshold λ

图7 平均纯净度pavg随阈值λ的变化曲线Fig.7 Change curve of the average purity pavg with the threshold λ

若λ较小,会使得聚类所形成的各个簇较小,簇的数量较多,来自于同一雷达的信号被划分至多个簇中,但此时各个簇的纯净度较高;当λ→0时,聚类所形成的簇均为单点簇,即被视为噪声。若λ较大,会使得聚类所形成的各个簇较大,簇的数量较少,来自于多部雷达的信号会被聚为一个簇,各个簇的纯净度较低;当λ→1时,所有数据点被聚为一个簇,纯净度达到最低。

为确定合理的距离阈值λ,引入k距离图。即各数据点到其第k个最近邻的距离排序后形成的曲线图,如图8实线所示为测试数据集的k距离图。图8中横轴n为排序后k距离序号,纵轴dk为k距离。

图8 k距离图Fig.8 k-distance graph

由于数据集中噪声点相对稀疏、有效数据点相对密集,因此k距离图中k距离较小且增长较为缓慢的区域代表的是有效数据点,而增长较快的区域代表噪声点,位于这两部分区域之间k距离变化率急剧变化的点所对应的k距离可作为距离阈值λ,该点称为“膝点”,即图8中的标记点。

为确定“膝点”,文献[15-18]提出了多种方法,但均计算复杂,为此提出一种距离确定法。如图8虚线所示,连结k距离曲线首尾两点,计算k距离曲线上各点到该虚线的距离,取距离最大点为“膝点”,“膝点”对应k距离为阈值λ。

由图8可知,对测试数据集使用本文所提距离确定法得到的阈值λ为0.053。该阈值对应的图6中的nr为10,表明聚类所发现的雷达数量为10;同时该阈值对应的图7中的pavg为99.50%,表明各个簇均有较高的纯净度。这表明使用本文所提距离确定法确定的阈值λ在被用于第2.1节所提聚类算法时,可有效发现数据集中存在的雷达。

2.3 连通k近邻聚类算法

综合第2.1节、第2.2节提出的连通k近邻聚类算法,算法描述如算法2所示。

算法 2 连通k近邻聚类算法输入:数据集X输出:簇标签1. 对数据集X进行标准化与归一化处理;2. 使用熵值法确定各维参数权重;3. 对各数据点进行k近邻搜索;4. 绘制k距离图,使用距离确定法确定阈值λ;5. 初始化并查集;6. 将各数据点与位于其λ邻域内的k近邻连通;7. 查询并查集,分配簇标签并返回。

为保证各数据点能够有效地与近邻连通形成簇,近邻搜索数目k与数据点维数m应满足

k≥2m

(1)

且k越大越好。而由对kd树的相关研究,当近邻搜索的搜索数目k与数据集中数据点数n满足

2k≤n

(2)

则对kd树的近邻搜索具有O(k·lbn)的时间复杂度。为保证算法效率与有效性,算法中k值可通过下式确定:

(3)

式中:m为数据点维数;n为数据点数。

由于基于k距离图的阈值距离确定法只需要遍历一条与数据点数n长度相同的曲线,因此时间复杂度为O(n);对各数据点进行k近邻搜索的时间复杂度为O(k·n·lbn);对并查集进行归并与查询的时间复杂度分别为O(k·n)与O(n)。由上述分析,本算法时间复杂度为O(k·n·lbn)。

本算法需要维护各数据点的k近邻以及并查集,空间复杂度分别为O(k·n)与O(n),因此本算法空间复杂度为O(k·n)。

3 算法仿真与对比

3.1 算法仿真

按第2.2节表1所示雷达列表生成序列时长为100 ms的雷达信号,并混合脉冲流密度为10 000脉冲每秒的噪声。使用连通k近邻聚类算法进行信号分选,分选所得簇标号统计结果如图9所示,横轴为簇标号,纵轴为簇标号频次;分选准确率如表2所示,准确率定义为各簇中正确分选信号数量占分选所得信号数量的比例。由分选结果可知,连通k近邻聚类算法在较为复杂的信号环境中能够实现正确分选。

图9 分选结果统计Fig.9 Statistics of sorting result

3.2 算法对比

为对比连通k近邻聚类算法与低复杂度模糊聚类算法用于信号分选的分选性能,将二者用第2.2节所述表1所列雷达参数生成的雷达信号数据集(为使低复杂度模糊聚类算法能够自动确定阈值,使用文献[24]所提出的使用CH指标确定最佳聚类的方法,阈值λ步进为0.05),重复运行5次分选,统计分选准确率如表3和表4所示。

表3 连通k近邻聚类Table 3 Connected k-nearest neighbor clustering

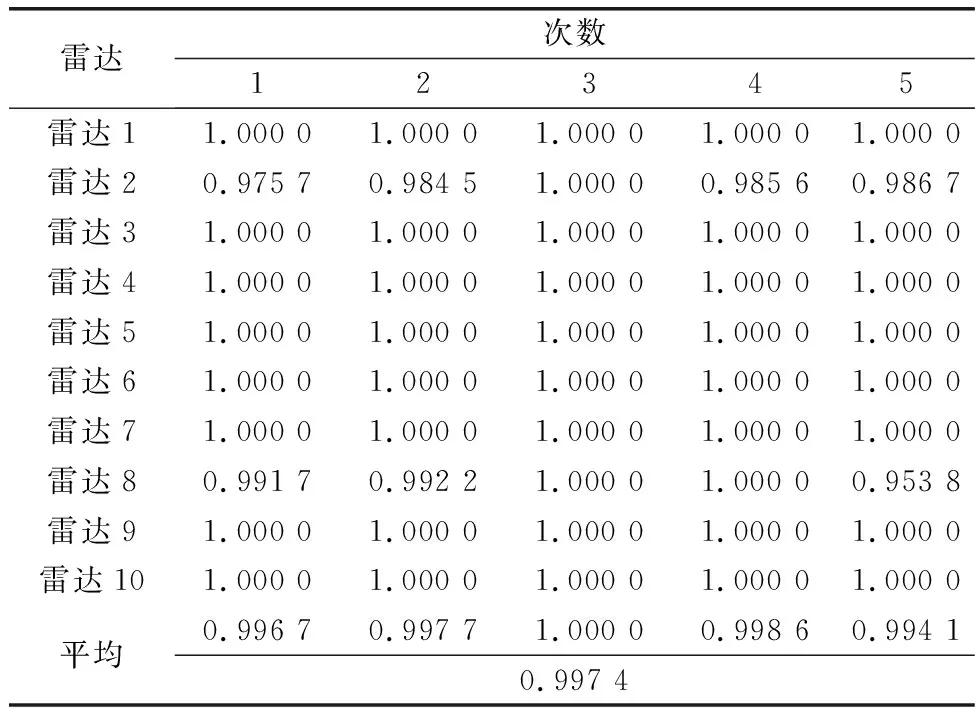
表4 低复杂度模糊聚类Table 4 Low-complexity fuzzy clustering

由表3和表4可知,连通k近邻聚类算法与低复杂度模糊聚类算法(使用CH指标确定最佳阈值)分选准确率相近,分选性能相近。

为对比连通k近邻聚类算法与低复杂度模糊聚类算法的时间复杂度,将连通k近邻聚类算法、低复杂度模糊聚类算法(使用固定阈值)、低复杂度模糊聚类算法(使用CH指标确定最佳阈值)应用于不同信号数量的数据集进行聚类分选,消耗时间曲线如图10所示。图中横轴为信号数量n,纵轴为算法运行消耗的时间t(由于时间差异较大,纵轴使用以s为基准的对数时间dBs)。由图10可知,所提算法相对于低复杂度模糊聚类算法,时间复杂度明显下降。

图10 3种算法消耗的时间对比Fig.10 Comparison of time consumption of three algorithms

3.3 算法缺点

本文所提连通k近邻聚类算法中,阈值的自动确定是基于噪声点相对于有效数据点而言较为稀疏的前提实现的。当数据集密度不平衡时,即信号环境中某雷达信号密度相对于其他雷达相差较大时,该雷达信号可能被当作噪声而丢弃。

按表5所示雷达列表生成序列时长为100 ms的雷达信号,并混合脉冲流密度为10 000脉冲每秒的噪声。使用连通k近邻聚类算法进行信号分选,分选准确率如表6所示。由分选结果可知,雷达5未被成功分选,这是由于雷达5的PRI较大,从而造成该雷达信号数量较少,密度较低,信号空间中分布稀疏,被连通k近邻聚类算法视为噪声而丢弃。因此,连通k近邻聚类算法不适用于密度不平衡的数据集。

表5 雷达列表(密度不平衡数据集)

表6 分选准确率(密度不平衡数据集)

4 结 论

为了能够在密集且复杂多变的信号环境中进行实时、有效的信号分选,提出了一种连通k近邻聚类算法。

(1) 使用k近邻搜索结合阈值的方式,相对于低复杂度模糊聚类算法,以空间复杂度增加为代价(由O(n)增加至O(k·n)),降低了时间复杂度(由O(n2)降低至O(k·n·lbn)),提高了算法的实时性;

(2) 提出了基于k距离图的阈值距离确定法,使得算法参数可根据信号环境自适应调整。

通过算法仿真对比,验证连通k近邻聚类算法与使用CH指标确定最佳阈值的低复杂度模糊聚类算法分选效果差距不大、性能相近,同时时间复杂度大幅下降;所提算法具有较低的时间复杂度以及无需人工设置聚类参数的优势,但其在面对密度不平衡的数据集时,聚类效果较差。