不确定环境下巡飞弹群动态资源管理

李 兵, 刘正敏, 赵新路

(四川航天系统工程研究所, 四川 成都 610100)

0 引 言

美国战略与预算评估中心2007年发布的《制导弹药与作战网络》[1]研究报告中明确指出,现装备的制导弹药对于大多数目标的精确打击问题已基本解决,但对于面目标,时间敏感和加固或深埋目标的攻击仍然是挑战。巡飞弹具有传统制导弹药所不能实现的一些功能,如攻击反斜面的洞内目标;在目标隐藏区域上盘旋监视与封锁;侦察并打击在崎岖道路上运动的目标等[2]。陆战场上可以深入敌方腹地,有选择性地打击高价值目标和时间敏感目标,适应城区作战、山区作战等不确定环境作战条件,以较小的投入换取较大的战场效益,是活跃在陆军信息化战场上的“幽灵”,担负陆军战术纵深内的点目标精确打击和任务地域协同封控等作战任务,不仅可以弥补传统炮兵弹道投送火力对时敏目标、活动目标、有遮蔽目标等类型目标打击能力的不足,而且通过侦察、打击、评估的一体化,可大幅提高对敌火力打击的综合作战效能[3]。

随着集群技术的进一步发展,通过巡飞弹群的自组网,实现网络化协同作战,能够实现全覆盖地毯式的封控压制和毁伤攻击,火力打击变化表现为,发射前瞄准或锁定的对象从目标变为区域,每次发射的效果从瞬间释能转变为连续封控与瞬间释能复合,火力打击方式变化产生“时空压制”新质能力,形成新的群蜂作战样式[4]。

作战任务的实现需要建立在对任务科学合理的管理基础上,这也是动态资源管理研究的出发点。实际应用中,战场环境的不可预测性、攻防双方的对抗性、目标信息的时变性等不确定因素,要求在实施作战过程中,根据作战任务使命,要在考虑对方所有可能的策略的基础之上选择有利于己方的策略,实现实时的最大作战效能。关于动态资源管理当前通用的做法是将目标抽象为多目标组合优化问题,Schumacher等为实现多无人机协同决策问题,利用网络流模型,以多无人机总的航迹最短为目标,面向具体的使命任务实现高效的协同任务分配[5]。文献[6-8]以无人机集群OODA(observation,orientation,decision,action)自闭环为作战任务,研究了无人机集群和目标规模不匹配问题,重点研究了集群规模大于目标数目饱和打击问题,利用最优化方法给出了协同决策最优任务匹配。文献[9]在研究动态目标分配问题时,以全局航行距离最短为目标,以OODA自闭环典型任务场景下,建立了动态任务分配模型,利用智能优化方法实现了任务分配。Marjorie等[10-11]在集中式任务分配问题中,利用遗传算法实现了巡飞弹群集中式协同任务分配。在分布式任务分配研究过程中,Wang等[12]采用合同机制利用Petri网实现了协同任务分配。文献[13] 考虑任务适应度和机群关系特征,针对任务需要多机协同完成现实需求,利用优化算法实现了协同任务分配。文献[14]设计了两层耦合的任务规划求解策略,利用模拟退火算法实现了协同对地打击任务分配问题。张赟[15]等利用空间自适应博弈算法实现了分布式任务分配。彭雅兰[16]等利用交替方向网络进化博弈的方法实现了无人机集群任务分配。谷旭平[17]等利用细菌觅食算法实现异构无人机协同任务规划。

动态资源管理的过程中往往会遇到巡飞弹或敌目标的动态加入和退出等问题。为了更好地利用和协调巡飞弹的资源,提高其作战效能,需要给出合适的方法来进行动态目标分配。本文首先对动态资源管理问题进行分析,给出了概念和内涵,其次建立了巡飞弹群的动态目标分配模型,并给出了主要的计算步骤,最后利用Hungarian算法求解了动态目标分配问题。

1 问题建模

为了更好地利用巡飞弹群的资源和提高弹群的作战效能。根据巡飞弹察打一体和一次性作战使用的特点,给出其目标分配的原则是在打击目标前保存自己,提高杀伤敌目标的概率,力求最大限度的发挥巡飞弹群的作战效能[18]。

同时部署n个巡飞弹构成巡飞弹群,不妨设巡飞弹具有相同的性能,每个具有固定值tmax的巡飞时间,则

V={1,2,…,n}

(1)

表示一系列部署的巡飞弹群。目标类型已知,这里用m来为目标编号,Nt表示被发现目标的数量并且T={1,2,…,Nt}。

动态资源管理问题的模型可描述为

(2)

式中:C=(Cij)n×m为威胁矩阵,Cij表示为第j个敌目标相对于第i枚巡飞弹的威胁程度;X=(Xij)n×m为目标分配解矩阵,Xij表示是否把第j个敌目标分配给第i枚巡飞弹,其值为0或1,1表示已分配,0表示未分配。

2 动态目标分配算法

2.1 复杂环境下目标对巡飞弹的威胁估计

未来信息化条件下的弹群集群作战将是以体系与体系对抗为特征的一体化作战。敌目标威胁评估是弹群中一项重要内容,同时也是动态资源管理系统中目标分配的基础。

目前,国内外对威胁评估进行了深入的研究,根据目标特点和规模采用的方法不同,主要包括:基于知识智能体的方法、基于模糊数学多准则决策系统、基于统计学Bayes推理、基于不确定的D-S(Dempster-Shafer)证据理论、博弈论、基于云计算模型推理的方法等。可以综合以上方法,结合具体任务提高威胁估计的准确度[19]。

威胁评估的目标是确定对方目标对我方形成威胁的程度,其可通过威胁要素提取、威胁度估计以及威胁等级确定来实现对威胁的估计。

(1) 威胁要素提取

对于巡飞弹群来讲,威胁主要来自防空、干扰、诱导等反弹群作战的威胁,其主要因素是威胁类型、敌我距离、威胁目标的速度以及敌打击、干扰或者诱骗的能力等。

(2) 威胁度估计

威胁度是充分考虑敌作战意图的前提下定量描述防空、干扰、诱导等对巡飞弹群威胁程度,利用概率计算的方法完成威胁要素统计分析,凝练敌威胁对巡飞弹群威胁程度的量化指标。

(3) 威胁等级确定

根据威胁度的估计,综合考虑目标特性和威胁程度,构建威胁等级的评价指标体系,判定敌目标的威胁等级。

2.2 巡飞弹群作战效率函数的构建

目标的威胁系数矩阵为C=(Cij)n×m,作为巡飞弹群任务决策模型中的效率矩阵。

本文将影响决策的要素分为如下两部分:一是敌目标对我弹群的威胁,二是弹群对敌目标的作战效能。根据使命任务,利用加权平均的方式将威胁和效能组合可以实现对敌目标不同的作战意图,具体步骤如下。

步骤 1面向使命任务,利用威胁估计的方法构建威胁矩阵,并进行无量纲归一化处理:

步骤 2根据巡飞弹平台的性能构建基于作战效能的效能矩阵,并进行无量纲归一化处理:

式中:B为效能矩阵,Bij为第i枚巡飞弹对第j个目标的攻击效能值。

步骤 3效率矩阵的构建方式如下:

Z=αC-βB

(3)

式中:Z为评价矩阵,C为威胁矩阵,B为效能矩阵,α,β为权重系数,满足0≤α≤1,0≤β≤1,α+β=1。根据作战使命可以选择优先对敌打击模式、优先巡飞弹群生存模式、打击和生存平衡模式以及自定义模式。根据实际需求,当选择已打击效能为目标的风险模式时,α=1,β=0;当选择保存弹群为目标效益模式时,α=0,β=1;当选择风险和收益均衡模式时,α=0.5,β=0.5;可自选权重值以决定攻击和防御的比重。

不确定环境下,敌我作战决策是一个典型的非合作非零和对策问题,本文根据巡飞弹集群作战的特点,综合考虑敌目标的威胁程度与弹群的效率函数模型进行动态目标分配研究。

2.3 动态资源管理Hungarian算法

Hungarian算法是基于Hall定理的二部图匹配最有效的算法,可快速高效的求解目标函数为线性函数、分配策略为敌我目标规模相当的优化问题。对于敌我目标规模不匹配问题[20],可利用增补变量的方法变成匹配问题,求解巡飞弹群的规模和目标的规模动态变化使得动态资源管理具有很好的扩展性,其步骤如下。

步骤 1效率矩阵的构建。

步骤 2根据矩阵行、列减去一个常数最优解等价进行效率矩阵的变换。

步骤 3根据定理Hall寻找最优解。

经过步骤2后形成新效率矩阵,新的效率矩阵利用步骤2中矩阵变换后求得行、列都有了0,根据Hall定理一定存在并m个相互独立的0。其具体操作步骤如下:

步骤 3.1标记只有一个0的行,不妨将0记作※,表示行所代表的巡飞弹对列对应的敌目标执行作战任务,然后划去※所在列,记作◎,表示列所代表的目标已被分配。

步骤 3.2标记只有一个0元素的列,将0元素记作※,然后划去※所在行。

步骤 3.3重复步骤3.1和步骤3.2,直到找不到包含1个0元素的行或列为止。

步骤 3.4经过步骤3.1和步骤3.2以后,如果存在至少2个0元素行或列,此时问题的解不唯一。可从含有0元素少的行或列进行标记,然后将同行或列中0元素忽略,反复步骤3.1和步骤3.2,直到矩阵中0元素标记或划掉。

步骤 3.5标记※的数目等于效率矩阵的维数,可得最优解。否则转至步骤4。

步骤 4标记※的数目小于维数,为得到效率矩阵中最多的独立0元素。其具体操作步骤如下:

步骤 4.1标注为标记※的行,记作X。

步骤 4.2标注X的行所包含0元素的列同样记作X;

步骤 4.3再对标注X的列所包含0元素的行记作X;

步骤 4.4重复步骤4.2和步骤4.3操作,直到结束;

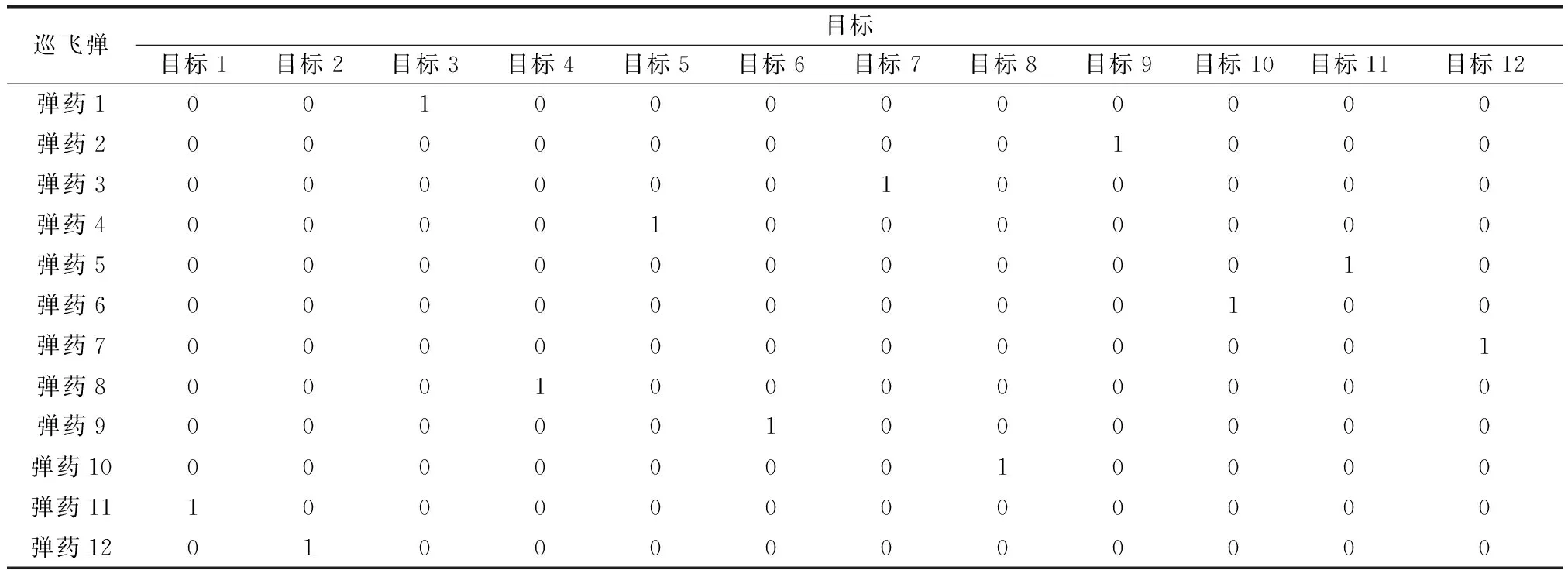
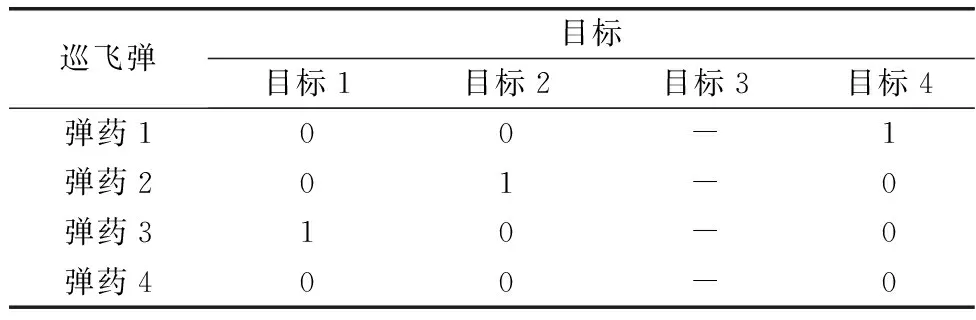
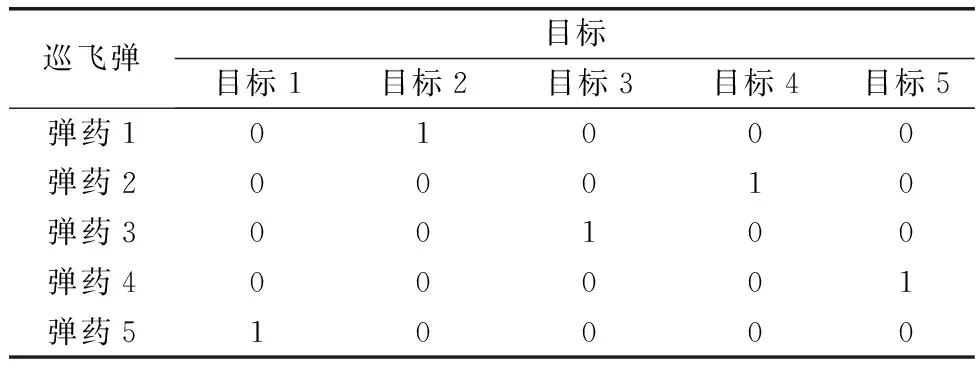
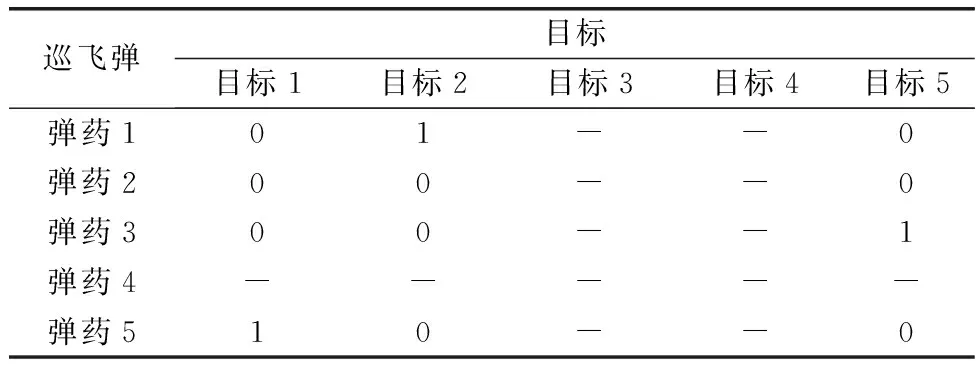
步骤 4.5横线划过未被标注的行,竖线划过未被标注的列,可得效率矩阵中全覆盖0元素的最少直线数。若k

步骤 5重新变换得到的效率矩阵是为尽快找到最优解,得到更多0元素。经过步骤4后行或列中还未找到最小值,将此行按照步骤2矩阵运算的性质减去最小值,此列都加上最小值,经过变换后得到n个相互独立的0元素,则为最优分配方案,否则回到步骤3重复进行。

2.4 不确定环境下态势变化及策略研究

敌我双方的态势通过效率矩阵来体现,态势分析是弹群作战过程中目标分配的基础,根据作战任务的需求,巡飞弹的动态加入或巡飞弹自身的故障及其他原因退出弹群。此时,进行目标分配时,根据效率矩阵的定义和变量的含义可利用增补变量(可取效率矩阵相应的行或列为较大数值)的方式实现突发状况的目标分配。

针对上述突发状况及复杂战场环境和目标时敏特性,使得战场敌我态势信息具有动态性,即效率矩阵中对应的元素随时间变化,为了得到稳定的目标分配结果,不妨构建一个稳定的目标分配机制,可设置一个体现作战的效能阈值,作为是否重分配的依据。

为了减少可能目标的丢失和重分配的计算量,当敌目标分配给巡飞弹并执行打击任务时,重新分配可能会导致原目标的遗漏,从而影响整体的作战效能。为提升分配效率,本文拟建立弹目一定条件下的锁定机制来确保在当前任务进程中,目标一旦锁定,被分配的巡飞弹不再参与其他作战任务。

3 动态资源管理算例分析

3.1 基于锁定目标的任务决策

将战场区域设置为2 km×2 km。巡飞弹从阵地打出后,快速由阵地介入到战场区域。其携带的探测传感器锁定目标的距离为200 m,敌我规模皆为12且初始任务分配的位置随机生成,如表1所示。任务分配结果如表2所示,1表示该行的巡飞弹打击该列的目标,后文同此。

表1 算例的初始条件

表2 基于Hungarian的任务决策方案

此时评价矩阵如下:

定义巡飞弹的锁定距离为200 m,所以当已配对的距离小于200 m时,则该敌目标已被锁定,从上述锁定距离矩阵来看,巡飞弹3、5、6分别对目标7、11、10进行了锁定,则锁定目标后任务分配结果如表3所示。

表3 基于锁定目标的任务决策方案

3.2 敌目标动态加入或退出战场

敌我目标规模均为4,此时若敌目标5加入战场,此时的评价矩阵如下:

计算可得到分配方案如表4所示。

表4 敌目标加入任务决策方案

若敌目标3由于自身故障或敌作战方案的需要退出战场,则根据本文构建规则,得到如下评价矩阵:

得到的分配结果如表5所示。

表5 敌目标退出任务决策方案

3.3 巡飞弹动态加入或退出巡飞弹群

巡飞弹动态加入或退出弹群时,弹群规模针对现有敌目标出现以多打少或以少打多现象,为此,重新分配任务。本文拟采用对初分配未使用的巡飞弹,采取作战效能最大,对弹群威胁最小策略来进行再决策。

巡飞弹5加入到弹群中,此时的评价矩阵为

按照新的策略经过计算得到的目标分配方案如表6所示。

表6 巡飞弹动态加入任务决策方案

巡飞弹3退出弹群,则按照规则得到如下评价矩阵:

按照二次分配的方法经过计算得到的目标分配方案如表7所示。

表7 巡飞弹退出任务决策方案

3.4 敌我双方各有单元退出的情况

设敌我双方规模为5,其评价矩阵为

利用Hungarian算法得到的目标分配方案如表8所示。

表8 基于Hungarian算法的任务决策方案(有退出)

此时,若巡飞弹4和敌目标3和目标4退出战场,则根据上述规则,此时评价矩阵为

按照二次分配的方法经过计算得到目标分配方案如表9所示。

表9 巡飞弹和敌目标退出任务决策方案

4 结 论

本文研究了不确定环境下巡飞弹群动态资源管理问题,充分考虑现实环境下,目标态势的动态更新和巡飞弹群规模的动态变化,利用增补变量的方式将非平衡匹配问题变为平衡匹配问题。数值实验中,本文方法较好地实现了平衡/非平衡问题的动态资源管理,比传统的最优化方法具有更好的扩展性,为巡飞弹群完成作战任务,实现科学的集群化“侦、控、打、评”提供了重要支撑,对推动巡飞弹群的实战化运用具有重要学术价值。