新高考背景下的数学建模教学探究——从一道跨学科融合题的命制说起

陈 敏 叶事一 林迪迪

(1.浙江省永嘉县罗浮中学;2.浙江省温州市教育教学研究院;3.浙江省永嘉县罗浮中学)

从近三年的新高考卷(即2020-2022年)、全国高考卷分析,高考中的基础性、综合性、应用性和创新性的“四翼”理念不断呈现.传统、机械化的题型正在被结构不良题、多选题、情境题等所取代,数学素养的考查尤为重要.题海战术已经无法适应高考,数学能力的培养成为考核的方向.高考正引领教学回归基础、回归规律、回归本质、彰显数学的科学价值.因此,在“以考选人,以考促教”的教育模式背景下,各地市积极开展了高考题型的研究.

数学建模是高中数学学科六大核心素养之一,也是新高考热门题型.该题型充分体现了“价值引领、素养导向、能力为重、知识为基”的命题理念,很好地体现了数学核心素养.但与此同时更为棘手的是在数学建模的过程中往往超越了数学学科的边界,需要与其他学科知识融合,通过各学科之间的支撑,完成建模过程.这就需要我们根据实际需要重组各学科的知识,构建全面的认知体系,并运用于教学实践中,形成跨学科融合教学.

笔者参与2021—2022学年温州市普通高中高一上数学期末考试的命卷、审卷以及后期数据统计工作.通过这次组织活动中,笔者通过数据发现学生对于数学建模能力严重不足,教师对于新高考研究以及对待策略欠缺.因此,笔者希望通过自行车建模问题生成过程,以及衍生出的跨学科问题,浅谈建模问题研究和应对的新策略.

1.高中数学建模

什么是数学建模?目前高中数学学科有六大核心素养,其中数学建模是对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型,解决问题的素养.具体的数学建模的过程,即数学建模所经历的分析问题、模型假设、模型建立、模型求解和模型检验这5个过程.而在平时的教学中,我们发现目前建模的概念和过程较为范广,基本等同于大学建模的概念.

笔者认为的高中数学建模,利用数学寻求现实问题的多快好省解决方案.从命卷的角度分析,除了传统的数学建模的五步骤,总结出学科融合建模的四部曲:“三归,一融”,即

1.1 归真——数学建模要回归到真实生活,回归到教材

模型引入：筒车问题(书本P231)与摩天轮问题(书本P238).

在人教版必修第一册三角函数中,课本典例中出现了筒车问题和摩天轮问题.筒车,中国古代发明的农业生产工具,为中国古代农业的发展提供帮助,成为璀璨的中国文化之一.新教材第一次出现(与旧教材),也是在三角模型的第一个问题,筒车中蕴含着中国数学文化史,体现中国古人利用数学创造生活、改善生活.摩天轮的问题进一步阐述了圆的三角形问题,特别体现三角函数中周期性变化的特征.

通过上述课本的两个例子,可以鲜明的发现数学与生活、文化等紧密联系一起,强烈体现了数学即生活.因此观察生活时,我们就能发现自行车,它是生活中常见的交通工具,特别是它的车轮就是圆形,当车轮运动时,其轮胎相对地面成周期性变化,符合筒车模型.进一步研究发现,自行车有两个轮胎,每个车轮上的都有点的运动轨迹,组成起来情况就多了,也复杂的数学问题.

1.2 归本——再复杂的数学问题最终还是数学

接下我们用另外一道纯数学——拓展题,思考自行车问题.

已知圆心在坐标原点的定圆O的半径为1,另外一个半径为1的动圆M始终与定圆外切,已知动圆上一点P(x0,y0)的初始位置在(1,0)处,当动圆在定圆外沿着定圆无滑动地滚动时,x0的取值范围是________.

解法一:如图建立平面直角坐标系,设∠MOA=θ,

显然M(2cosθ,2sinθ),

延长MO交定圆于C,则C(cos(π+θ),sin(π+θ)),

逆时针旋转θ,则P1(cos(π+2θ),sin(π+2θ)),

利用平移,可得P(cos(π+2θ)+2cosθ,sin(π+2θ)+2sinθ),

∴x0=2cosθ+cos(π+2θ)=2cosθ-cos2θ=-2cos2θ+2cosθ+1,

当cosθ=-1时,(x0)min=-3,

解法二:延长MP交x轴于D,过点M作x轴垂线,垂足为E,过点P作PF⊥ME于F.

设∠MOD=∠OMP=θ,

∴∠MDE=2θ.

∵PF∥DE,

∴∠MPF=2θ,

显然OE=2cosθ,PF=cos2θ,

∴x0=OE-PF=2cosθ-cos2θ,

接下来过程同解法一.

显然此题已经属于较难题范畴,解决问题的基本有两种思路.第一种:学生引入平面直角坐标系,目标以代数形式完成解决,显然定圆的圆心O(0,0),半径r=1,动圆圆心C(2cosθ,2sinθ),这些坐标点较为容易.难点是动点P该如何表示,根据题意,则运动的弧长一样,即转过相同的弧度角.利用对称性,将动圆的动点转换到定圆上,则P1(cos(π+2θ),sin(π+2θ)),转化得出P(cos(π+2θ)+2cosθ,sin(π+2θ)+2sinθ),即x0=2cosθ-cos2θ,显然就是三角函数的计算.再通过二倍角,以及二次函数的性质,较容易计算可得.第二种:学生利用几何图象,通过构造两个直角三角形,把横坐标直接用OE-PF表示,最终回到三角函数计算.显然,第二种方法易求不易想,偏向初中的方法,缺陷是只能解决锐角问题,其他角的研究还需要说明.第一种建系,常规而基础,是高中生需要掌握的基本能力.

1.3 归合——通过不断演示检验模型的合理性

如图,自行车前后轮半径均为rcm(忽略轮胎厚度),固定心轴间距|O1O2|为3rcm,后轮气门芯P的起始位置在后轮的最上方,前轮气门芯Q的起始位置在前轮的最右方,当自行车在水平地面上往前作匀速直线运动的过程中,前、后轮转动的角速度均为ωrad/s,经过t(单位:s)后P,Q两点间的距离为f(t).

(Ⅰ)求f(t)的解析式;

(Ⅱ)求f(t)的最大值和最小值．

【解析】(Ⅰ)如图建立平面直角坐标系.

∴|PQ|2=(xP-xQ)2+(yP-yQ)2=[3r+r(cosωt-sinωt)]2+[r(cosωt+sinωt)]2,

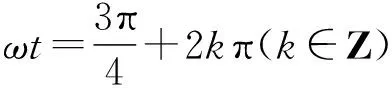
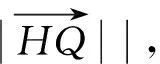
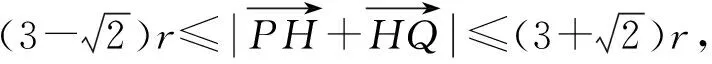
通过问题1和问题2对比,如何建立适当的平面直角坐标系是解题的关键点和共同点,但是数学问题生成的过程也存在差异,筒车研究纵坐标的变化得到余弦,双圆问题研究横坐标变化得到正弦,而车轮问题研究点与点之间的距离得到正、余弦.从逻辑上,考查知识点的螺旋上升,不再局限书本的概念,关注概念的生成过程,“授之以渔”的教学模式进入数学建模课堂.

2.数据背后的思与教

2021年温州市高一期末考试采取分卷考核,即为A,B卷(A卷为一类学校,B卷为二、三类学校),自行车模型同考核,分别是A卷的21题,B卷的22题.从题型分布看,建模题以压轴题的形式出现,从命题者角度认为,一类学校建模教学更为有效,学生落实较为扎实,情况真是如此吗?

2.1 学生的实际情况

从自行车模型题的成绩数据来看,A类学校(代表使用A卷学校,后面类同,不再说明)学生平均分为1.86分(满分12分),标准差为3.182 9分,区分度0.383 4,B类学校学生平均分为0.33分,标准差为1.130 5分,区分度0.073 6.两份试卷结果远远低于预期,A类学生两级分化显于B类,即“优生通吃”原则,但大部分学生基本无法动笔,跨学科融合与数学建模创新性成为学生“噩梦”,充分暴露出学生数学创新能力、素养能力、建模能力的缺失,知识掌握不扎实,学习停留表面.

从试卷整体失分情况分析,有几方面:一、学生概念不清,抽离不出与之对应数学模型或者建立错误模型;二、运算能力不足,学生在求点或者计算时出现错误;三、字迹潦草,步骤错乱;四、时间安排不合理,缺少思考时间;五、创新能力不足,仍习惯于应试模型.

2.2 教师的教学现状

对于数据分析,让我们深刻明白学生自身学习态度和能力不足,同时也在反思教师的教学.从调查数据看,目前大多数一线教师对于建模题态度往往分成两类:1.因为题目简单,不需要讲太多,学生自然而然会做;2.题目难度较大,许多时候讲了学生不一定会,部分教师选择不讲,通过简单讲述思路及答案,随意带过.绝大部分教师,会讲解但是重心在计算上,忽略最原始的生成过程;3.不重视知识生成过程,往往依靠习题或者题海落实教学.这种教学,往往让中下层学生忽略数学建模的核心价值,失去对建模的兴趣,甚至产生恐惧心理,背离了数学建模的核心素养.

2.3 教师建模的教学改进

从命卷角度出发,做好五点建议:(1)回归课本,回归概念,特别是核心概念,需要教师强化辨析,深化数学理解;(2)数学问题的讲解,注意回归数学逻辑,重视计算能力;(3)加强情景题,建模题的整理和练习,培养学生阅读能力和抽取数学问题能力;(4)教学过程中,重视知识交叉,关注跨学科的知识融合,培养学生立意能力;(5)增加探究式、开放式的课堂,让学生学会用数学的角度看待问题.

3.结束语