基于高考情境化试题的命题研究
——以四省联考数学试题为例
朱 彬 胡晓静
(1.湖南省长沙市南雅中学;2.湖南省长沙市雨花区雅境中学)
2023年度高考蓝皮书《中国高考报告(2023)》中,对2023年高考数学命题变化提出“考试加入复杂情境”,这一变化在不久前出炉的由教育部命制的四省(安徽、云南、吉林、黑龙江)联考数学试题中得以落地生花,整套试卷突出情境命题,像球形几何、圆周率中的强弱率、开关阵列、养鱼、椭圆曲线区块链等新颖情境试题悉数登场,既融入了中国传统文化,又体现了中国现代数学的应用,充分呈现出“无情境,不成题”的特征,对2023年的全国新高考复习备考有着非常明确的指导意义和导向作用.为此,本文对四省联考出现的新情境试题进行研究,并从中得到教学启示,供2023届全国新高考地区师生在临考阶段复习备考时参考.
一、试题解析
1.新定义情境
这类题型是指试题给出中学数学没有出现过的一些新概念、新性质、新符号、新运算等情境,在读懂、理解新定义的基础上,要求考生主动思考,通过将新定义信息迁移,建立新知识与已有知识的联系,进而分析并解决问题.
【例1】(2023·四省联考·22)椭圆曲线加密算法运用于区块链.

(Ⅰ)当4a3+27b2=0时,讨论函数h(x)=x3+ax+b零点的个数;

(Ⅲ)已知P(x1,y1)∈C,Q(x2,y2)∈C,且直线PQ与C有第三个交点,求P⊕Q的坐标.
参考公式:m3-n3=(m-n)(m2+mn+n2).
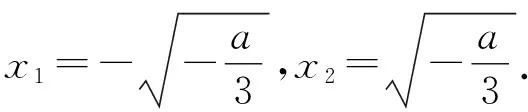
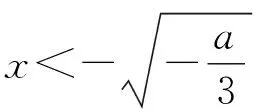
当b>0时,h(x2)=0,所以h(x)有2个零点;
当b<0时,h(x1)=0,所以h(x)有2个零点.
当a=0时,b=0,则h(x)有1个零点.



【点评】本题情境丰富,对数学素养要求高,既有新定义运算情境,又有高等数学情境;既考查导数在求解函数单调性中的应用,但又不全尽然,需要在充分阅读、理解所给信息的基础上,通过推理论证才能完成解答,有效考查数学抽象、逻辑推理、数学运算等核心素养,是一道情境颇为新颖的压轴题.
2.新设问情境
这类题型在设问角度或方向上进行创新,要求考生能综合运用所学知识进行探究,分析问题并最终解决问题.
【例2】(2023·四省联考·8)已知a,b,c满足a=log5(2b+3b),c=log3(5b-2b),则
( )
A.|a-c|≥|b-c|,|a-b|≥|b-c|
B.|a-c|≥|b-c|,|a-b|≤|b-c|
C.|a-c|≤|b-c|,|a-b|≥|b-c|
D.|a-c|≤|b-c|,|a-b|≤|b-c|



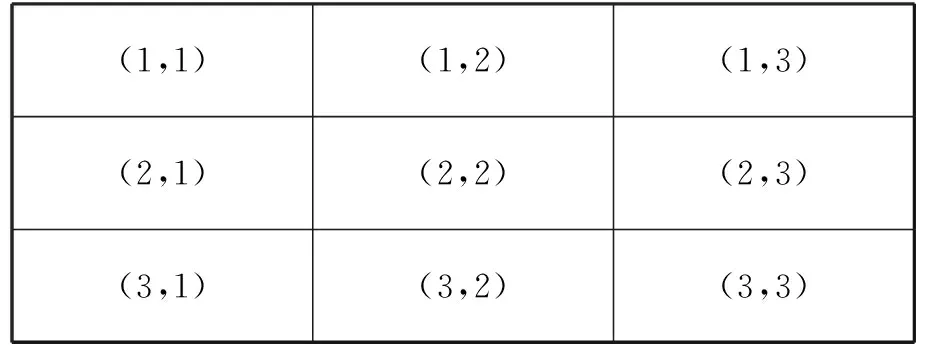
故a 当0 【点评】本题作为单选压轴题,从题设条件到选项的设置,其情境都十分的新颖.求解本题的方法较多,若从单选题的题型特点考虑,可有下面的“秒杀”方法:当b→0时,a→log52,c→-∞,可知选B.请大家体会. 这类题型往往不囿于单一的知识点,而是强调知识间的整合,在知识的结合点处创新情境进行命题,这是高考数学命题的一种重要趋势. ( ) 综上,故选ABD. 【点评】本题设置三角函数模型在物理质点的圆周运动中的应用情境,结合物理内容考查三角函数的知识和应用,体现了跨学科间的相互支撑、相互补充,这类情境问题有意识地将数学与其他学科交叉、融合,对于促进学生学习能力、数学思维能力和创造性思维能力的发展具有很大的作用. 这类题型的命题载体往往打破常规,不受某些知识覆盖面的约束,与数学学科中的内容也没有直接和太多的联系,不是课本中固有的知识或模型,但对理解、分析、判断和逻辑推理能力却有着较高的考查要求. 【例4】(2023·四省联考·16)如图为一个开关阵列,每个开关只有“开”和“关”两种状态,按其中一个开关1次,将导致自身和所有相邻的开关改变状态.例如,按(2,2)将导致(1,2),(2,1),(2,2),(2,3),(3,2)改变状态.如果要求只改变(1,1)的状态,则需按开关的最少次数为________. (1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3) 【解析】把9个开关分成两组:A组为(1,2),(2,1),(2,3),(3,2);B组为(1,1),(2,2),(1,3),(3,1),(3,3).按下A组开关可改变偶数个开关的状态,按下B组开关可改变奇数个开关的状态.若只改变(1,1)的状态,则B组开关必须按下奇数次.另外,按下同一个开关两次不会改变任何状态,所以为了让次数尽可能小,每个开关最多只按一次. 根据上面的分析,按下(1,1),(1,3),(2,3),(3,1),(3,2)可使得最终只改变(1,1)的状态,且不存在按开关次数更少的方法. 故需按开关的最少次数为5. 【点评】本题不属于某个数学知识点,而是在阅读图表、理解分析的基础上进行推理判断的,考查了数学抽象、逻辑推理及直观想象等核心素养. 这类题型以弘扬中华传统文化,增强数学文化浸润,吸收世界数学文化的精华为情境命题,引导学生热爱数学文化,体现立德树人总目标的要求. 【点评】本题以圆周率为命题情境,给出弱率和强率的定义,并以此进行分析、推理解答.我国古代的数学家在圆周率方面的研究,成绩特别突出.祖冲之对圆周率的研究成果,让我们感到十分骄傲和自豪. ( ) A.sinβ=sinγcosδ B.cosβ=cosγcosδ 故选ACD. 【点评】本题以元代数学家郭守敬在编制《授时历》时所做的天文计算为命题情境,在渗透数学文化的同时,考查了空间几何体线面垂直的判定与性质及三角函数定义的应用,考查逻辑推理核心素养. 这类题型注重从高中到大学的衔接,将大学有关的高等数学知识下放,以高等数学知识为情境命题,然后应用中学所学的知识解答,既可以开阔考生知识视野,有利于考生完成初等与高等知识的和谐衔接,又能够考查考生运用高中知识分析、解决问题的能力及数学核心素养.比如例1第22题的椭圆曲线,例6第12题的球面几何,例7的极大似然估计等,都是高等数学情境、中学知识解答的典型试题. 给出现实生活、生产实际、科学研究等问题情境,与数学知识、方法建立联系,构造并转化为相应数学模型,应用数学工具解决问题. 【例7】(2023·四省联考·20)一个池塘里的鱼的数目记为N,从池塘里捞出200尾鱼,并给鱼作上标识,然后把鱼放回池塘里,过一小段时间后再从池塘里捞出500尾鱼,X表示捞出的500尾鱼中有标识的鱼的数目. (Ⅰ)若N=5 000,求X的数学期望; (Ⅱ)已知捞出的500尾鱼中15尾有标识,试给出N的估计值(以使得P(X=15)最大的N的值作为N的估计值). (Ⅱ)当N<685时,P(X=15)=0; 故当N=6 666时,σ(N)最大,所以N的估计值为6 666. 【点评】本题以实际应用情境考查超几何分布的概率公式、数学期望公式的应用.其实该题是试验研究中常用的“标志重捕法”,让考生用中学数学知识诠释概率论与统计知识的可行性,衔接高中与大学的数学知识,考查“数学的应用”. 解答数学情境化试题一是要全面审视各相关材料之间的关系,注意问题的整体结构;二是要寻求合理解决问题的思路、方法和途径,其思维过程的程序框图是: 具体地说,1.阅读材料,理解题意:弄清题目中材料所表达的含义,并进行比较、分析、综合、抽象与概括,领悟其数学实质,为制订解题策略作准备. 2.整合材料,明确方向:在阅读材料、理解题意的基础上,有目的地对外来的和内在的信息进行提取、转化、加工、整合和传输,从而明确解题的目标与方向. 3.联想类比,分析求解:联想、类比、转换为相关知识或方法,采用适当的步骤,合乎逻辑地进行推理判断或演算,实现解题目标. 2023年度高考蓝皮书《中国高考报告(2023)》在高考评价体系内在的三条逻辑线中有这样一段描述:“通过合理创设情境,设置新颖的试题呈现方式和设问方式,促使学生主动思考,发现新问题、进行新解释、找到新规律、得出新结论.”无论是从这段描述还是从四省联考数学试题中,可以预测2023年高考命题将更加重视对情境创新性的考查,这就要求我们在临考复习备考阶段重视和加强对数学创新型问题的研究.那么,高考复习中应注意哪些问题?下面提出几方面建议,供读者参考. 1.高考数学命题复杂情境越来越多、越新,阅读理解、计算要求也越来越高,在教学中,教师需要引导学生加强针对数学情境化试题的训练,进一步提高阅读理解、推理论证和探索求解能力.要想让学生考出理想的成绩,复习中要多指导学生提升阅读量,不惧怕试卷中题干较长的题目,而是迎难而上,抽丝剥茧般分析究竟想表达什么意思. 2.复习备考要重视抓基础知识的理解和变通;重视典型题目中的基本方法总结,哪个方法在什么情况下使用要理顺;要引导学生注重思考、总结和自主探究,这样可以在一定程度上提高解决创新问题的能力. 本文系长沙市教育科学院“十三五”规划课题“信息技术与中小学数学生命化课堂的深度融合研究”(CJK2019014)阶段性成果.
3.知识结合情境



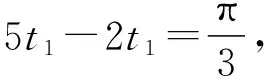
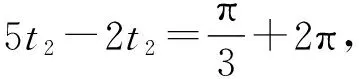

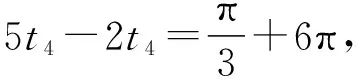
4.新载体情境
5.数学文化情境

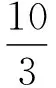

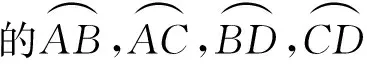
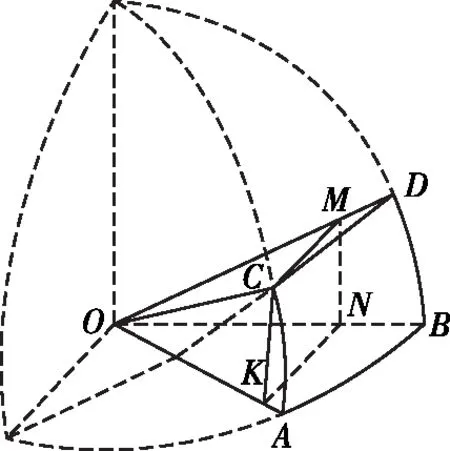





6.高等数学情境
7.实际应用情境




二、方法程序

三、教学启示


