认知诊断中缺失数据的插补方法比较研究

陶怡汐，牛彦敏，刘馨媛

（重庆师范大学 计算机与信息科学学院, 重庆 401331）

0 引言

与传统测验只能得到被试的一个测验分数或者能力值不同，认知诊断利用现代统计方法和计算机技术作为工具，能够诊断出被试当前的认知水平，找出被试的认知优势与不足，为个体的因材施教及有针对性地开展补救教学提供服务[1]。认知诊断理论自从产生以来，引起国内外学者的广泛关注，至今已有大量认知诊断的相关研究。认知诊断中个体数据的完整性十分重要，然而由于一些主观和客观原因，诊断过程中不可避免地会出现数据缺失的情况。PAN 等[2]的实验证明，随着样本中缺失率的增大，诊断准确率会下降。因此，缺失数据是认知诊断中亟需解决的问题，并且需选用合适的插补方法进行缺失数据处理。

针对缺失数据有3 类处理方式：加权法、删除法和插补法。加权法， STEPHAN 等提出抽样概率的倒数加权法解决单元数据缺失情况[3]，其原理是将缺失单元的权数分解到非缺失单元上，从而增大非缺失单元的权数以减小缺失单元所带来的影响，主要用来处理单元性数据缺失问题，只适用于随机缺失的情况。删除法，又包括对象删除和属性删除，对象删除即直接删除数据集中某个存在缺失的对象，属性删除则是当数据集中某属性存在缺失时就直接删除该属性。删除法操作简单，速度快，但仅适用于缺失率较小的数据集，一旦数据集中缺失数据较多，删除法会使得数据集丢失过多的信息，从而影响后续实验结果的准确性。插补法，有报道提出对缺失值进行插补以获得完整数据的方法。与删除法去除缺失数据相反，插补法的原理是为每一个缺失数据找到替代值，以此获得完整数据集。之后出现了均值插补[4]、回归插补、最近距离插补、冷卡插补等多种数据插补方法。在此前研究的基础上，DEMPESTER 等研究者对极大似然估计方法进行改进，提出了期望最大化算法[5]，该算法利用迭代计算实现对缺失数据的处理。以上几种方法都属于单值插补，这类方法填充值是唯一的。RUBIN 基于贝叶斯理论，提出了多重插补法[6]，其基本思想是为缺失值推断出多个估计插补值，并产生多个完整数据集进行综合分析，确定最终的估计填充值。它吸收了期望最大化算法的优点，克服了单一插补的缺点，提高了数据插补的准确率。随着机器学习在各领域掀起了热潮，如何利用机器学习方法有效地处理缺失数据问题成为了研究的重点。目前，代表性的方法有：K-means插补、贝叶斯网络等。2012 年STEKHOVEN 等研究者基于随机森林[7]，提出了缺失森林算法，它可以直接利用已检测到的完整部分数据集训练出的随机森林来预测缺失值。加权法和删除法虽然具有操作过程简单的优点，但是它们都具有容易丢失有用信息和误差大等缺点，相较于此，新的插补法具有稳定性高、误差小等优点，成为数据缺失处理研究的重点方向。

缺失数据的插补处理在医疗、经济、心理统计等领域的应用较为广泛[8-11]，但近年来少有针对认知诊断中的缺失数据处理问题的研究。2001年DE AYALA 等探讨了项目反应理论中省略回答对能力估计准确性的影响[12]；2008 年FINCH 进行了缺失数据情况下项目反应理论参数的估计[13]；2020 年PAN 等通过实验证明，诊断模型参数的恢复率随着损耗率的增加而降低[2]；2021 年周昱希基于个体属性掌握概率以及个体之间的最短距离提出了认知诊断评估中缺失数据的插补方法[14]；同年，马驰将XGBoost 方法引入认知诊断领域，提出了一种可容忍缺失值的机器学习诊断法[15]。

至今为止，在认知诊断的相关研究中，对于不同的样本量和缺失率对插补效果的综合比较与评估仍然较少。本实验将缺失森林方法引入认知诊断中，在模拟实验中，将其与常用的几种缺失处理方法，零替换、均值插补、多重插补、期望最大化算法进行比较，评估在不同情况下各种方法的插补准确率以及对下游诊断结果的影响。此外，为了验证实验的有效性，以国际学生评估项目（PISA）2015 科学素养数据为实例，进一步比较评估各方法在实证数据中的处理效果。最后讨论并总结了在不同情况下各种插补方法的效果，丰富了认知诊断缺失数据处理的研究，为同类研究提供借鉴。

1 方法原理

1.1 缺失数据产生原因

在社会测验中，由于各种原因，产生缺失数据的情况不可避免，在认知诊断中也是如此[16]。认知诊断中造成数据缺失的原因除了被试能力不足以外，还可能包括被试的答题动机不强，被试的精神状态不佳导致题目与答题卡配对错误，测试时间安排不当，测试题目偏离测试目标，设备故障、断网、网速不快耽误作答等原因。

1.2 数据插补方式

1.2.1 零替换（Zero Replace, ZR）

零替换，即将诊断过程中缺失的作答视为错误答案，并用“0”替换缺失数据，再将插补之后的完整数据集输入诊断模型，进行下一步的分析处理。ZR作为认知诊断中处理缺失数据传统方法，虽然执行简便，但会导致统计效力和参数估计精度的下降，因此有学者并不建议使用。

1.2.2 均值插补（Mean Imputation, MEAN）

均值插补[4]就是用研究数据中已观测到的数据平均值作为缺失数据的插补值，作为一种操作简便且快速的缺失数据处理方式，与众数、中位数等插补方法同属于传统统计插补，其缺点为容易造成变量方差和标准差变小，相对而言更适用于分布较为平均且已知样本量信息较多的数据插补问题。

1.2.3 多重插补（Multiple Imputation, MI）

多重插补[6]作为缺失数据处理方法的一种，其插补过程大体为插补、分析和合并3 个步骤。首先，对存在数据缺失的原始数据集选择相应的模型方法，进行n 次插补，每插补一次就会得到一个独立的完整数据集；然后，对这n 个完整数据集应用模型的标准方法进行分析，检验数据集是否合格；最后，综合分析结果，选择最优的数据集作为最终的完整数据集。

本研究选用二级计分形式，MI 系列方法中的分类回归树方法（Classification and Regression Trees, MI-CART）、预测均值匹配（Predictive Mean Matching, MI-PMM）均适用于二分变量插补[17]，下面介绍这2 种方法的原理和基本步骤：

（1）MI-PMM。其大致步骤为：首先，根据排除了缺失条目的完整数据集建立模型，计算预测值；其次，使用所建立的模型计算出所有条目的预测值，从预测值最接近缺失条目预测值的所有完整数据中形成一个捐献者小集合；最后，从捐献者小集合中随机抽取数据替换缺失数据。

（2）MI-CART。其大致步骤为：首先模型根据最佳切分点对数据样本进行多次切分，将数据切分为2 个子样本；其次，经过多次递归切分直到数据不可再分，同时每个子样本中的数据都是同质的，此时分类回归树就构建好了；最后，根据构建的分类回归树，找到每一个缺失数据下的终端子样本，并从该子样本中随机抽取数据作为插补数据。

1.2.4 期望最大化算法（Expectation Maximization Imputation, EM）

期望最大化算法[5]是一种求参数极大似然估计的方法，主要通过迭代计算处理不完全数据，每一个迭代过程都由期望步和极大化步组成。期望步，依据已有的数据和上一次迭代参数求缺失数据的条件期望值；极大化步，根据期望步所求的条件期望值来替换缺失值，并用极大似然估计法重新计算出新的参数，用于下一次迭代。最后不断重复以上2 步，直到目标函数收敛。

当数据规模巨大时，EM 算法的执行非常简单，只需要通过自身的迭代过程就可以找到全局最优解。但EM 算法的速度由缺失数据的多少决定，缺失数据的比例越大，算法收敛速度越慢。

1.2.5 缺失森林（missForest）

缺失森林是由STEKHOVEN 等[7]提出的一种基于随机森林的迭代估算方法，用来解决缺失数据问题。它可以直接利用已检测到的完整部分数据集训练出的随机森林来预测缺失值，而不依赖于因变量的完整性，既可用于连续型变量也可用于离散型变量。假设X=(X1, X2,…, Xp) 是一个n×p 维的矩阵，对于任意变量记为Xs，缺失森林的插补步骤为：首先对X 的所有缺失数据进行初步的估算( 用均值插补或者其他方式插补)，然后将变量Xs根据缺失值的数量进行从小到大排序，从最小的数量开始依次使用随机森林回归去填补缺失值，重复计算过程，直到满足停止标准，即插补数据的结果变化较小或不再变化。

1.3 诊断模型

本研究认知诊断部分选用DELATORRE提出的G-DINA模型[18]，此模型在诊断过程中考虑到了属性之间的交互，更加符合实际情况，其常见的公式为

2 实验

2.1 模拟实验

2.1.1 实验设计

本研究采用3×3×6 的完全交叉实验设计，其中自变量为被试数量、缺失率和缺失数据处理方式。被试数量包括了3 个水平(100 人、500 人、1 000 人)，分别对应小样本、中样本和大样本；分别设置了3 种缺失率（10%、20%、30%）；缺失数据处理方式选用EM、MEAN、MI-PMM、MI-CART、ZR、missForest 6 种方法。

2.1.2 模拟过程

完整数据生成：本实验采用GDINA 包的simGDINA（）函数模拟被试的作答反应，其中滑动概率和失误概率都固定设置为0.1。共有10 道试题，考查3 个属性。

缺失数据生成：通过R 软件中的simFrame包构建不同缺失率的缺失数据样本。

缺失数据处理：使用R 软件、SPSS 23.0 和PyCharm 2022 实现。选用SPSS 23.0 实现均值插补和ZR 处理。MI 方法调用R 软件中的MICE 包实现，插补次数均设置为20 次，以保证插补结果的准确性。同时用R 软件中的EMimpute（）函数实现EM 处理。missForest 方法则通过自编的Python 代码实现，树的数量设置为450。

2.1.3 评价指标

本文选用均方根误差RMSE（Root Mean Square Error）作为插补性能评价指标，其公式为

插补实验过后，本文选用模式判准率PMR（Pattren Match Ration）作为评价被试属性掌握的估计精度的指标，公式为

其中N 为被试数量，Ni-correct表示第i 个被试的属性掌握模式的分类结果与该被试真实的属性掌握模式是否一致，一致为1，否则为0。模式判准率越高，代表被试的属性掌握模式判断正确的数量越多。

2.1.4 模拟实验结果

对含有缺失值的模拟数据集进行插补处理之后，本研究计算了每个插补数据集和其对应的完整数据集之间的RMSE，以此来比较各方法的插补准确率。

表1 和图1 呈现了在不同样本量与缺失率组合下，6 种插补方法进行数据处理之后的均方根误差结果。首先，从整体上看，随着缺失率的上升RMSE 会逐步增加，同时样本量的增大也会导致RMSE 的增大，证明随着缺失数据量的增大，所列各种处理方法的插补准确率都会出现一定程度的下降。其次，在中样本（500 人）和大样本（1 000 人）条件下，基于随机森林的missForest是最优的处理方法。其余5 种方法在不同样本水平上的表现略有不同，例如在小样本（100 人）水平下MI-PMM 的处理效果最优，而在中样本以及大样本的条件下，MI-CART 的处理效果则优于MI-PMM。最后，MEAN 和ZR 这2 种方法作为最早期出现的插补方法，虽然操作简单，但RMSE均较大，插补准确率远低于其他4 种方法。

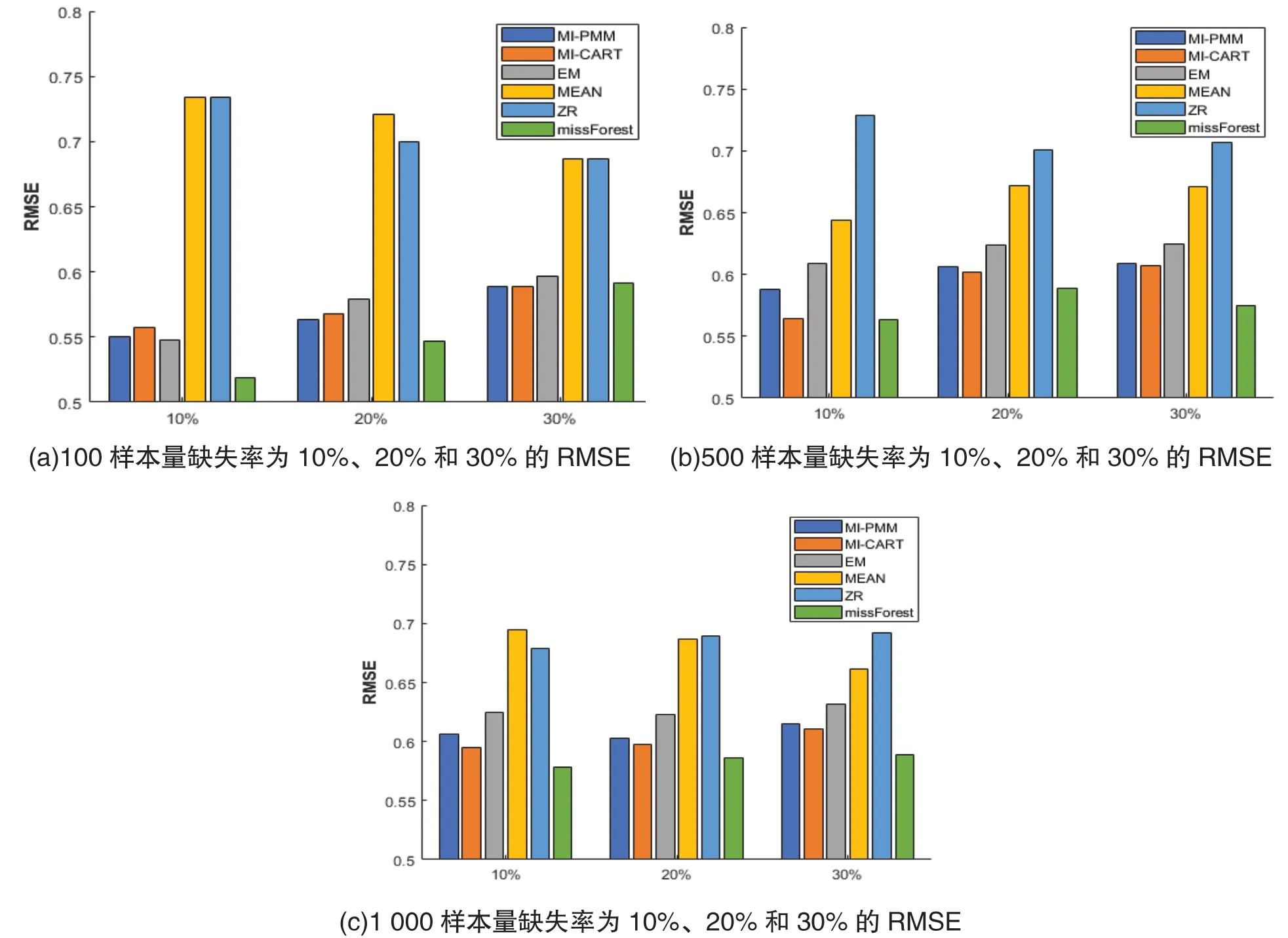
图1 不同样本量和缺失率下各处理方法的RMSE 对比

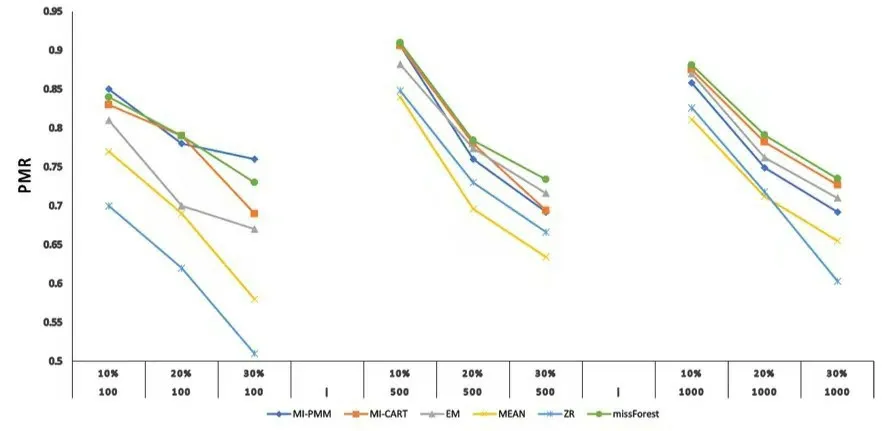
图2 不同样本量和缺失率下各处理方法的PMR 对比

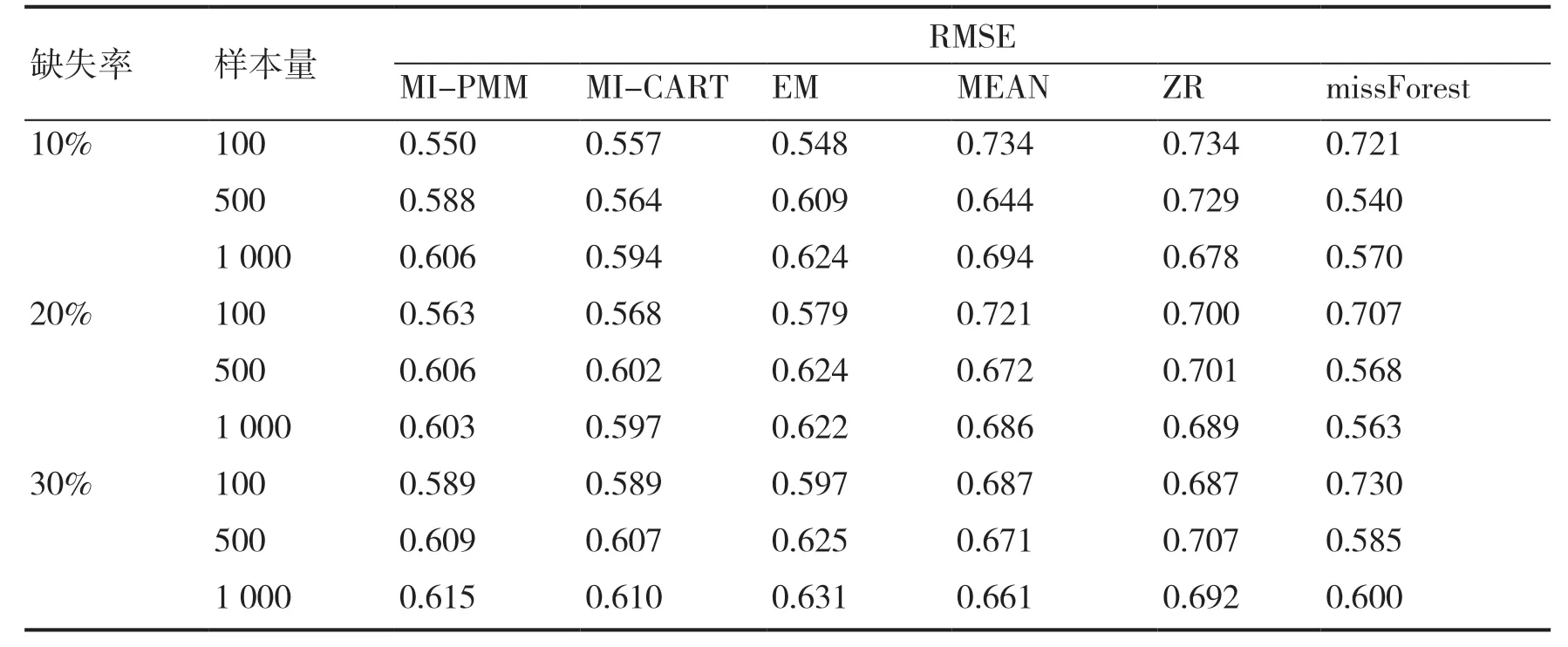
表1 均方根误差RMSE

从结果可以看出，在小样本中MI 的2 种方法的处理效果都较好，其中MI-PMM 和MICART 的效果相近，可任选其中一种。missForest的插补准确率较差，因为missForest 作为一种机器学习的插补方法，在小样本数据中由于已检测到的完整部分数据集较小，训练出的随机森林预测缺失值的准确性有待提高。而在中样本以及大样本中，missForest 的插补准确率优于其他。因此，在小样本条件下推荐选用MI 处理方法；中样本和大样本条件下，优先选用missForest 方法。

此外，本研究还计算了PMR，以此来比较各方法处理后的被试属性掌握的估计精度。

从表2 中可以看出，模式判准率的估计结果基本符合RSME 估计结果。missForest 在大样本量的实验中，取得了比其他方法更好的判准率。如1 000 样本量，在10%、20% 和30%的缺失率下，识别率分别达到了0.881、0.791和0.735。而在小样本量下，相较于多重插补方法， missForest 的表现稍差一些。如100 样本量，10% 和30% 的缺失率下，missForest识别率比MI-PMM 要低0.01 和0.03。这个结果与RSME 估计结果基本一致，可能主要是由于多重插补方法是基于原始含数据缺失的数据集进行插补，然后对多次插补的数据进行评估。因此在小样本下，多重插补方法更有可能插补出与原始数据相似度高的结果。所以，多重插补方法在小样本量下比其他方法表现得更好。

表2 模式判准率PMR

在缺失率方面，随着缺失率的增加，PMR 也在不断下降，而missForest 在一定程度上缓解了这个下降的过程，尤其是在较高缺失率的情况下。

因此可以得出，在大样本的情况下，missForest总体表现更好。而在小样本的情况下，选用多重插补方法更佳。

2.2 实证研究

2.2.1 实证数据

PISA 是国际学生评估项目（Programme for International Student Assessment）的简称，作为当前世界上最具影响力的国际学生成就评价项目之一，主要测试考察被试的阅读素养、科学素养和数学素养。2015 年PISA 能力测试主要考察的是科学素养，其中《PISA2015 科学框架草案》将科学素养分为如图3 所示的3 种能力[19]。

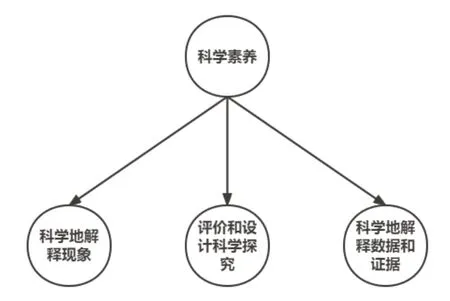
图3 PISA2015 科学素养

科学地解释现象，即认识、提供和评价对一系列自然现象和技术产品的解释。

评价和设计科学探究，即科学地描述、评价科学研究，提供问题解决的方法。

科学地解释数据和证据，即分析评价数据和各种不同方式表示的参数，并能得出恰当的科学结论。

本实验首先根据文献[20] 选用考查科学素养的18 道题目，筛选中国的1 092 名被试进行分析，除题目DS498Q04 之外其余题目作答结果均为二分变量，0 表示作答错误，1 表示作答正确，5-9 表示空缺，其次对于DS498Q04，将它转化为二分变量，即0 →0，1 →0，2 →1。最终得到题目数量, 被试数量的作答数据集，最后使用模拟实验中6 种方法对缺失数据进行处理，并用G-DINA 模型进行估计。实证实验数据集如表3 和4。

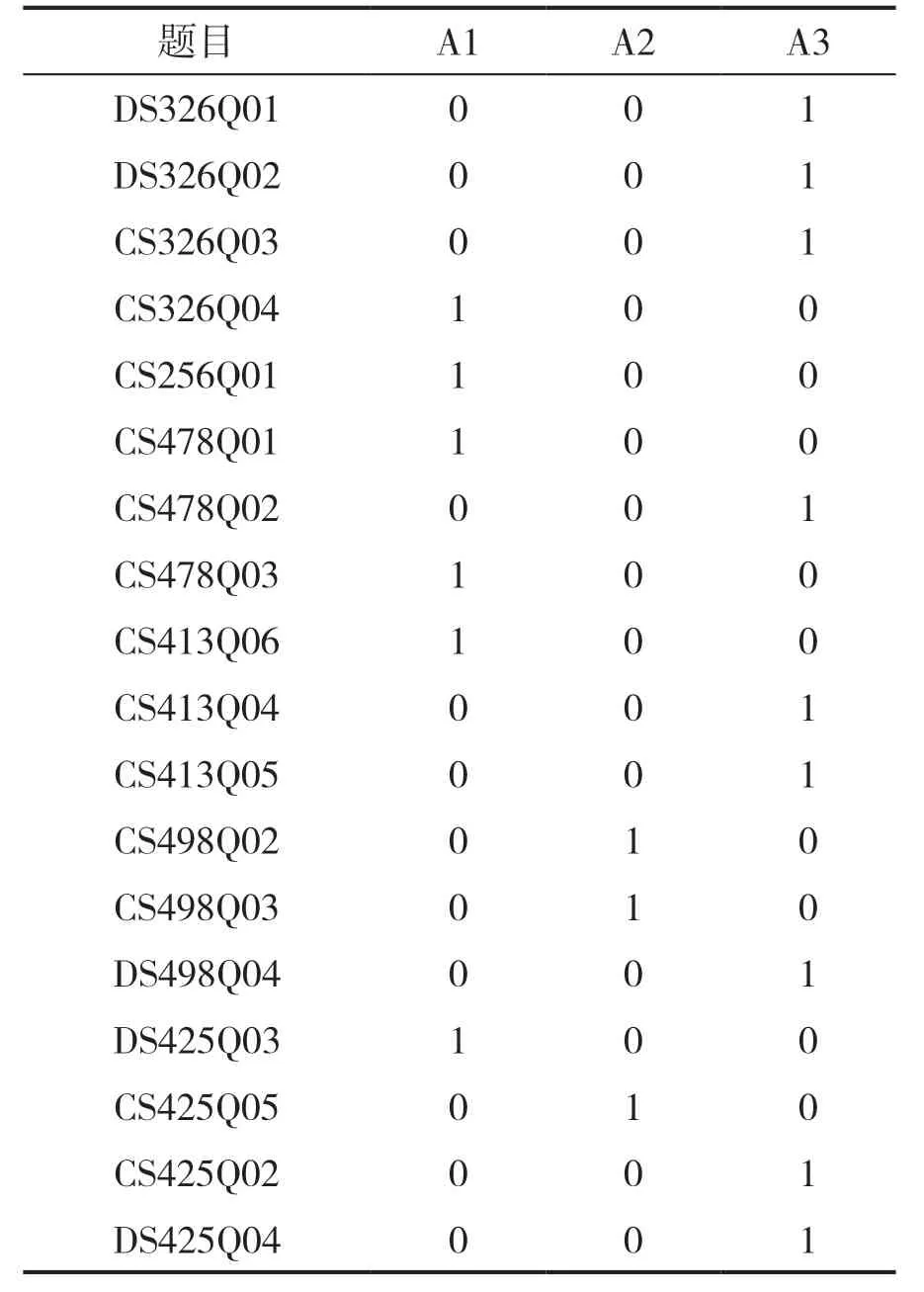
表3 实证实验Q 矩阵

表4 实证实验学生作答情况

2.2.2 实证结果分析

认知诊断过程中模型拟合主要分为项目拟合、测验拟合和被试拟合，由于本数据集选自PISA2015，实证研究选用以下几个评价指标：偏差(Deviance)、赤池信息准则(AIC)和贝叶斯信息准则(BIC)，指标值越小，表明数据与模型拟合程度更高，则该处理方法的效果更好。

实证研究结果如表5 所示，比较3 项指标，missForest 表现最佳，之后依次为MEAN、ZR、MI-CART、MI-PMM、EM。 实 证 研 究 中missForest 方法最优，与模拟实验中结果相似。但值得注意的是传统插补方法在实证研究中同样表现出色，究其原因在PISA 这类国际性大型测试中，被试重视程度高、答题动机强，测试时间安排得当，被试由于自身原因忽视答题或由于环境原因被迫退出答题的可能性较小，作答情况出现空缺是因为被试不会此题而跳过的可能性较高，因此可根据实际数据情况选择合适的插补方式。实证研究验证了所提方法的实用价值。

表5 实证结果

3 结论

本研究通过模拟实验对EM、MEAN、MIPMM、MI-CART、ZR、missForest 6 种插补方法进行了综合比较和评估，并通过实证数据进行了验证。发现随着缺失量的增加，各插补方法的插补准确率均下降。同时，在小样本中MI的填补准确率和模式判准率最优，而在中样本和大样本情况下，missForest 表现最佳。没有一种缺失插补方法在所有情况下均表现得最好，几种方法各有所长，可在不同情况下选用不同的方法。

目前，认知诊断中缺失数据处理的研究较缺乏，本研究可以为研究者在认知诊断中进行数据预处理时提供参考，此思路也可用于其他领域的缺失值填补效力评估。