航空发动机拆装车结构的轻量化优化及校核

程 林，朱 烨

（滁州职业技术学院 机械与汽车工程学院，安徽 滁州 239000）

0 引言

飞机发动机作为飞机的心脏及动力源，被誉为“工业之花”，其制造工艺要求复杂，装配过程更是精益求精。因此，长期以来西方资本主义国家将发动机拆装车的工艺参数、结构尺寸及性能要求等数据，看作国家机密实施垄断。

我国对飞机发动机拆装车的研究历史较短、经验较少，但多年来经过大量科研人员的不懈努力，发展势头也较为迅猛。其中武汉大学的郑继波[1]对飞机发动机拆装车的起吊装备进行探讨，并对发动机拆装车的吊装装备进行静态力学的有限元分析，校核各姿态下发动机拆装车的结构强度和刚度，但局限性较为明显，如吊装设备精准定位较差需多次操作。大连理工大学的雷海峰[2]、赵哲[3]致力于研究拆装车的数控调姿平台，开发出一种数控编程智能监测拆装车系统，但该系统的体积和质量均过大，缺少结构的轻量化优化。

发达国家在飞机发动机拆装领域研究起步较早，已经掌握了一套极为完备的装配工艺。早在20 世纪50 年代，以美国为代表的西方国家开始致力于研发液压驱动调资拆装系统，主要服务于早期战斗机发动机的拆装。经过二十多年的发展，美国研发了一种新型的紧凑型液压助力拆装车，实现双层导轨结构。发展到现阶段，西方发达国家在飞机发动机装配领域已基本实现标准化、通用化、机械化、智能化等一整套完备体系。

1 建模及材料

图1 所示为处理后的飞机发动机拆装车的三维模型，其具体参数见表1。对三维模型进行简化处理是必不可少的环节。删除对分析结果影响小的特征，可以缩短有限元计算的时间。在简化过程中必须考虑合理性，要保证分析结果可靠。在不研究工艺角应力、应变情况下，尽可能删除这些工艺角，以免在画网格时出现网格质量不好而导致无法收敛的现象。

图1 三维模型

表1 尺寸参数

图2 所示为划分后的网格数模。利用ADAMS软件建立完整的数模，将该数模保存为IGES 格式，导入到Analysis 分析软件中，便于后续数模的前处理及有限元分析。其详细信息：单元总计807 779个，其中CTETRA 单元为321 328 个，CQUAD4 单元为356 231 个，CTRIA3 单元为4 342 个，CONM2单元为5 个，CPENTA 单元为4 053 个，CHEXA单元为100 432 个，模拟螺栓连接为66 个，模拟焊接单元为21 327 个[4]。

图2 网格数模

在划分好的网格数模中赋予单元材料属性，本文发动机拆装车采用高强度的碳锰钢(16MnL)[5]，材料的具体机械性能见表2。

表2 材料机械性能

2 拆装车轻量化设计

常见的轻量化设计方法分2 种：其一，采用密度更低、力学性能更为优异的新型材料取代原先的材料，这种方法更为简单、直接和快捷，但质量更轻、力学性能更优越的材料，通常意味着成本更高，提取和制造工艺更复杂，不利于企业的投标[6]；其二，在不更换原材料的基础上，且保证工程结构力学性能达到设计要求的情况下，一定程度上减少材料的使用，从而达到减少整个工程质量的效果。客观上对比，第二种轻量化设计方法优势更为明显，更有利于企业控制成本[6]。

为保证发动机拆装车整体结构强度及力学性能，对于某些承载较大或应力较大零部件，不进行轻量化优化（如升降机构及4 个支撑腿）；而将那些受载较轻或受应力较小的杆件，作为本次轻量化优化的对象[7]。考虑到杆件的装配及位置要求，同时也为了便于计算，只改变杆件的厚度（不改变杆件的长度及截面长）。本次轻量化以体积最小化为原则，其数学优化模型如下[8]：

其中，式（1）中V 为优化单元的总体积；Vi为单个优化单元的体积；n 为优化单元的总数量；式（2）中σmax为所有优化单元中应力最大值；σp为材料的许用应力（数值为220 MPa）；式（3）中xi为目标变量， xiL和 xiU分别为目标变量的下限及上限[9]。

3 杆件灵敏度分析及优化

为保证航空发动机拆装车整体结构强度，在拆装车接触应力最大的工况基础上，选择接触应力较小的53 个杆件作为优化目标，将其厚度定义为目标变量进行轻量化优化。在进行轻量化仿真时，需对目标变量设置上下限数值，优化后的数值需在该范围内。本次轻量化数值的设定在现有模型尺寸的基础进行赋值，设定杆件轻量化前的厚度值为上限值；Analysis 仿真软件中的Optimization 模块，根据目标杆件的材料、原始厚度及接触应力值，系统给出下限值[10]。本次选择轻量化杆件的序号及轻量化前后杆件的厚度值如表3 所示。

由表3 可知，杆件经轻量化后其厚度均存在不同程度的减薄，如杆件8 最大减薄率高达50%，最小减薄率也接近12.5%(如杆件22)。拆装车轻量化前整车质量约为2000 kg，经仿真计算后可得，轻量化后飞机发动机拆装车整体结构质量降低185 kg，较轻量化前下降了9.25%。因此，对发动机拆装车进行轻量化设计显得尤为必要，有利于企业控制成本，避免产品质量过剩[11]。

4 模态对比分析

为探究轻量化前后发动机拆装车模态的变化，现对轻量化前后的拆装车进行模态分析（图3）。

图3 轻量化前后拆装车前四阶模态云图

图3 (续)

图3 为轻量化前后拆装车前四阶模态云图，根据云图绘制仿真结果如表4 所示。

表4 拆装车前四阶模态对比

由表4 可知，轻量化后拆装车前四阶固有频率较轻量化前略有上升。因轻量化后拆装车部分零部件的厚度存在不同程度减薄，致使发动机拆装车的强度及刚度稍有降低，同时伴随着低阶固有频率的微涨。较轻量化前，一阶固有频率从13.05 Hz 微涨至13.66 Hz，涨幅接近4.7%；二阶固有频率从13.65 Hz 微涨至13.98 Hz，涨幅仅有2.4%；三阶固有频率从之前14.27 Hz 微涨至14.96 Hz，涨幅4.8%；四阶固有频率从轻量化前的16.43 Hz微涨至轻量化后的17.11 Hz，涨幅接近4.1%。对于前四阶模态振型而言，轻量化前后拆装车振型一致，且轻量化前后拆装车前四阶固有频率涨幅均低于5%，说明飞机发动机拆装车整体结构的优化，对前四阶模态频率及振型影响较小。

参考纯电动汽车在市区路面的激励，因市区路面极为平整，路面对整车激励频率均低于3~4 Hz。而发动机拆装车大多工作在内场，其路况整体水平较市区更为平整光滑，因此内场拆装车的路面激励频率也低于3~4 Hz。本文发动机拆装车采用伺服电机驱动，因其电机运转极为平稳，即使低速行驶也极少出现振动的现象，同时兼有抑制共振的作用，所以伺服电机振动频率可忽略。轻量化后发动机拆装车最低激振频率为13.66 Hz，远高于内场路面激振频率3~4 Hz，因此轻量化后拆装车整体结构完全可避免共振的产生，满足模态要求。

5 力学性能校核

现对轻量化前后飞机发动机拆装车的强度及刚度进行校核，其目的在于对比轻量化对拆装车结构强度及刚度的影响，同时进一步确保轻量化后拆装车的整体结构符合设计要求。表5 为拆装车工作状态时的约束条件。

表5 约束条件

图4 为该约束下轻量化前后的位移及应力云图。

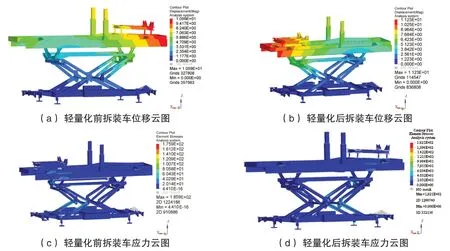
图4 轻量化前后拆装车位移及应力云图

由图4（a）及4（b）位移云图可知，该约束下轻量化前拆装车最大位移量为10.59 mm，轻量化后最大位移量为11.23 mm，相比增长了6.0%，且最大位移位置均为拆装车承载侧的端部及滑架的端部。虽然轻量化前后最大位移量增长了6.0%，但较拆装车整体尺寸而言变形较小。因此，轻量化后拆装车满足整体刚度设计要求。

从图4（c）及4（d）可知，该约束下轻量化前拆装车最大应力值为175.9 MPa，轻量化后最大应力值为182.1 MPa，相比增长了3.5%，且最大应力位置均为拆装车轴线滚转升降机构右侧连接的支撑板处。其最大应力值远低于碳锰钢（16MnL）材料许用应力值220 MPa。因此，轻量化后拆装车的强度满足设计要求。

6 结论

以自主设计的某型号的飞机发动机拆装车为研究对象，以体积最小化为轻量化优化原则建立数学模型，确定优化目标，经仿真计算后可知，轻量化后拆装车整体质量降低185 kg，较轻量化前下降了9.25%。为确保优化后的拆装车整体结构符合设计要求，对其模态及力学性能进行模拟仿真。发现，轻量化后拆装车低阶模态的固有频率及振型变化较小，涨幅均低于5%；正常工况下的最大应力值及最大位移量，虽分别增长了6.0%和3.5%，但仍在合理范围内。因此，轻量化后的拆装车整体满足设计要求。