含不凝气体的蒸汽凝结换热数值研究

郭庆, 罗凯, 耿少航, 秦侃

(1.西北工业大学 航海学院, 陕西 西安 710072; 2.西安电子工程研究所, 陕西 西安 710100)

0 引言

为适应现代海洋探测与攻防的需求,无人水下航行器必须在航速、航程与航深等方面寻求进一步突破,这对水下动力系统提出了更高要求[1]。电动力系统在电池能量密度、安全性等方面尚存在限制[2]。对于热动力系统,常见的开式循环系统存在航深适应性缺陷[3];闭式循环系统的运行不受环境影响,但技术难度大,在锅炉反应器等方面还有许多问题有待研究[4]。半闭式循环系统在主机后部增加了乏气增压排放装置,大幅减小了环境压力对主机运行的不利影响,是水下热动力系统的发展方向之一。

在半闭式系统中,为缩小装置尺寸、减少增压耗功,通常需进行乏气快速冷凝。一种应用于水下航行器的半闭式系统结构如图1所示,该动力系统采用由OTTO-Ⅱ推进剂、高氯酸羟胺(HAP)和水组成的三组元燃料[5],燃烧产物如表1所示,其中含有大量水蒸气等可凝可溶成分。

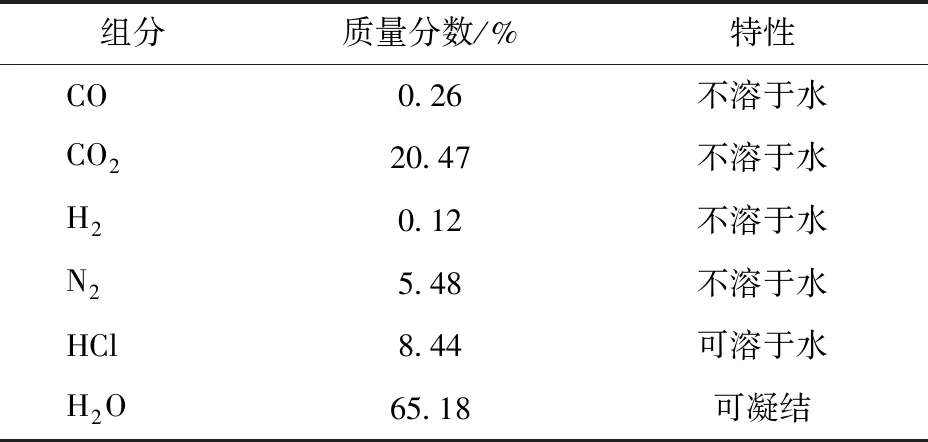
表1 HAP三组元推进剂燃烧产物组成

图1 半闭式循环动力系统结构示意图

在半闭式系统中,可采用图2所示的套管式海水换热器进行乏气冷凝,其中外流道为海水流道,内流道为乏气流道,乏气在换热器中的冷凝过程可抽象为含不凝气体的蒸汽凝结换热过程。系统正常运行时,由于两相泵的抽吸作用,换热器工作压力较低;当系统启动或切换高速时,两相泵的转速变化滞后于燃气流量的增加,泵前压力大幅升至超过舷外压力,单向阀开启并泄压,直至两相泵转速达到设定值,系统回归正常运行状态。为使工质体积快速下降并维持系统运行,在这一过程中换热器仍需正常工作,此时的工作压力等于舷外压力。本文研究的动力系统的最大航深为1 000 m,意味着换热器必须在 10 MPa 的高压力下正常工作。

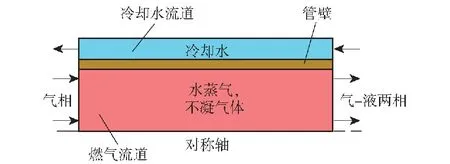
图2 套管式换热器结构示意图

海水换热器能否在全工况下有效进行乏气的降温冷凝,对半闭式系统的构型研究至关重要。对高压力条件下海水换热器内部含不凝气体的蒸汽凝结换热特性进行研究,是海水换热器性能研究的重要组成部分。针对含不凝气体的蒸汽凝结换热过程,各国学者进行了一系列试验与仿真研究。

凝结换热试验研究可对传热传质现象进行直接观察与测量,所得结果可作为理论与数值模型的基础与验证,现有的试验研究重点关注冷凝通道结构与不凝气体类型对凝结换热的影响。Kuhn等[6]和Kuhn[7]通过竖直管中含不凝气体的蒸汽凝结换热试验研究,提出了可用于计算通道内换热系数的削弱因子算法。Lee等[8]对竖直管道中含氮气的蒸汽凝结换热规律进行分析,认为小尺寸通道的界面应力能削弱不凝气体对蒸汽凝结换热的抑制作用。Ren等[9]试验分析了水平圆管含不凝气体的凝结,发现了圆管顶端与底端的非均匀换热现象。马喜振[10]通过试验分析了自然对流条件下工况参数对含不凝气体蒸汽凝结换热的影响,认为在压力较低时,换热系数随压力上升而增大,直至达到某一临界压力值。Park等[11]试验研究了强制对流条件下含不凝气体的蒸汽凝结换热特性,并拟合了由凝结液膜雷诺数、不凝气体质量分数和雅可比数组成的换热关联式。Ji等[12]对超疏水表面的蒸汽凝结换热现象进行了试验研究。

随着计算流体力学的逐步发展,研究人员基于实际现象进行合理假设,运用相关理论建立了多种数值计算方法,这些方法可以用于对含不凝气体的蒸汽冷凝过程的细节进行捕捉与分析。Fu等[13]忽略凝结液膜的影响,建立了含不凝气体的蒸汽凝结数值模型,并采用Kuhn试验方法进行了验证。Alshehri等[14]数值分析了不凝气体质量分数对气膜热阻的影响,认为随不凝气体质量分数的减小,凝结液膜热阻与不凝气体气膜热阻逐渐接近。Groff等[15]对比了不同湍流模型在含不凝气体的蒸汽凝结换热问题中的表现,认为k-ε模型具有较好的精度。Bian等[16]数值研究了不同管束情况下含不凝气体的蒸汽凝结换热特性,认为多排管具有更高的换热系数。Zschaeck等[17]基于扩散层理论建立了含不凝气体的蒸汽凝结换热数值模型。顾成勇[18]数值研究了不凝气体的质量分数变化时蒸汽凝结换热特性的变化。耿少航等[19]研究了高压下含不凝气体的蒸汽凝结问题,认为高压下不凝气体对蒸汽换热的抑制作用被削弱。

表2列出了上述部分研究的工况范围,目前对含不凝气体蒸汽凝结问题的研究主要针对较低的压力范围(通常小于1 MPa)[20],而对于本文所讨论的高压换热器,其根据工况的不同,工作压力可能达到10 MPa。为此,本文考虑重力的影响,建立了含不凝气体的蒸汽高压换热器数值计算模型,分析了水平管换热器中燃气流道的流动与换热特性,并讨论了管径对换热特性的影响;搭建了套管式高压换热器试验装置,通过试验验证了计算方法的可行性。

表2 部分已有研究涉及的工况范围

1 研究方法

1.1 数值方法

本文采用ANSYS Fluent软件[21]进行数值仿真计算,所采用的控制方程为

1)连续方程:

(1)

式中:ρ为密度;v为流体速度;Smass为质量源项。

2)动量方程:

(2)

式中:p为静压力;μ为黏度;I为单位张量;g为重力加速度;Fmom为动量源项。

3)能量方程:

(3)

混合气体中的扩散方程可写为

(4)

式中:Yj为组分j的质量分数;Dj和DT分别为组分j在混合工质中的质量和热扩散系数;Sct为湍流施密特数;μt为湍流黏度;Dt为湍流扩散系数。

在蒸汽的凝结方面,采用改进的Lee相变模型,因此蒸汽质量源项可定义为

(5)

式中:coeff为相变因子;αv为当前蒸汽体积分数;ρv和Tv为蒸汽密度和温度;Tsat为蒸汽饱和温度。相变因子的选取对于蒸汽冷凝过程的计算十分重要[22],较小的相变因子将导致气-液相界面温度与饱和温度存在偏差,增大相变因子有助于减小这种偏差,但可能导致计算难以收敛[23]。相变因子的取值与多种因素有关,目前多采用经验判断与试算调整相结合的方法进行参数选取。经过多次试算,本文将相变因子取为10 000,此时在计算中气-液相界面温度与饱和温度的最大偏差小于1%。

动量源项Si-mon和能量源项Senergy可分别定义为

Si-mom=viSmass

(6)

Senergy=Smassh

(7)

式中:下标i可替换为轴向和径向的对应下标x或r;h为水的汽化潜热,可利用美国国家标准与技术研究院物性参数库进行查询,并拟合为关于饱和温度的关系式:

(8)

本文采用SSTk-ω湍流模型[24],该模型具有较高的模拟精度和数值稳定性,是工程实践中广泛采用的湍流模型。另外,本文通过用户自定义函数将质量、动量和能量源项加载至控制方程中,以模拟含不凝气体的蒸汽凝结换热现象。速度-压力耦合方法选取Coupled算法,采用Geo-Reconstruct方法捕捉气-液交界面。计算采用稳态求解,基于入口条件对整个计算域进行初始化,当监测到的固体壁面热流密度和混合气体出口温度均到达稳定时认为计算收敛。上述数值计算模型已利用Kuhn[7]试验进行了验证,具体可参见文献[19]。

1.2 试验装置

考虑到本文研究的高压工况在已有试验中较少涉及,为进一步验证本文所采用数值计算方法的正确性,搭建高压下含不凝气体的套管式换热试验装置,并进行验证试验。试验装置的实物图与原理图分别如图3(a)和图3(b)所示。试验装置的工作原理是:将燃料通入燃烧室燃烧,得到含不凝气体与水蒸气的高温高压燃气,将燃气以及冷却水相对通入套管式高压换热器的燃气与冷却水管道,并通过在管道中设置的多组压力与温度传感器检测换热器内部的换热特性。试验装置由燃气发生系统、水供应系统、高压换热器、废气处理系统、数据采集与控制系统等组成。

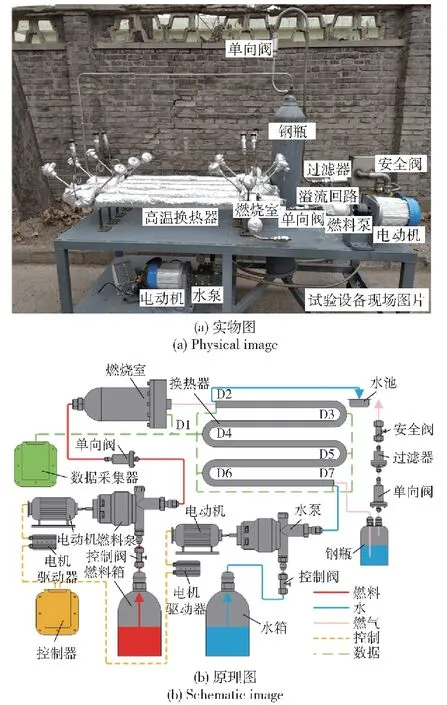
图3 套管式换热器试验设备

燃气发生系统用于为试验装置提供含不凝气体与水蒸气的高温高压燃气。现阶段,由于HAP三组元燃料的燃烧控制尚不成熟,本文试验的燃料采用水下动力系统常用的OTTO-Ⅱ单组元燃料[25]。OTTO-Ⅱ单组元燃料燃烧产物的主要组分为CO、CO2、N2和H2O,虽然其不凝气体与水蒸气的质量比例与HAP三组元燃料有所差异,但两者在高压换热器中的换热机理是相同的,因此使用该燃料进行试验依然能得到具有指导意义的试验结果。试验进行时控制阀打开,燃料泵电机带动燃料泵工作,将OTTO-Ⅱ燃料泵送至燃烧室燃烧以形成高温高压燃气,并向高压换热器的燃气通道输送。燃烧室内设有测点D1以监测内部压力,燃烧室前设置有单向阀以防止回火。

水供应系统用于为试验系统提供换热用水。试验进行时,控制阀打开,水泵电机带动水泵将水箱中的水泵送至高压换热器的冷却水通道。高压换热器为逆流式套管式换热器,其结构如图4所示。

图4 高温换热器结构示意图

换热器中心流道为燃气通道,半径5 mm,外圈环状流道为冷却水通道,高度1 mm。换热器总长5 m,为便于布置,将其分为5段,每段1 m,之间用半圆段连接并设置测点。换热器材料为不锈钢,管壁厚度1 mm,管外包裹有隔热保温材料,以尽可能减小试验时的能量损失。

数据采集与控制系统用于试验工况的控制以及参数的采集。数据采集方面,在换热器中每隔 1 m 设置一个监测点,每个监测点设置2个温度传感器与1个压力传感器,以检测冷却水通道的温度以及燃气通道的温度和压力,传感器精度为5‰,在试验误差分析时,认为参数测量的概率分布为均匀分布,置信因子取1.73[26]。工况控制方面,通过电机控制器调控电机转速,以实现对燃料泵和水泵流量的控制。

1.3 计算模型

本文主要研究含不凝气体的蒸汽凝结换热过程,采用图5所示的几何模型。该模型为三维面对称计算模型,只包含燃气通道,通道轴向为z轴方向,坐标原点位于通道入口截面几何中心处。燃气通道长度2 m,直径20 mm。

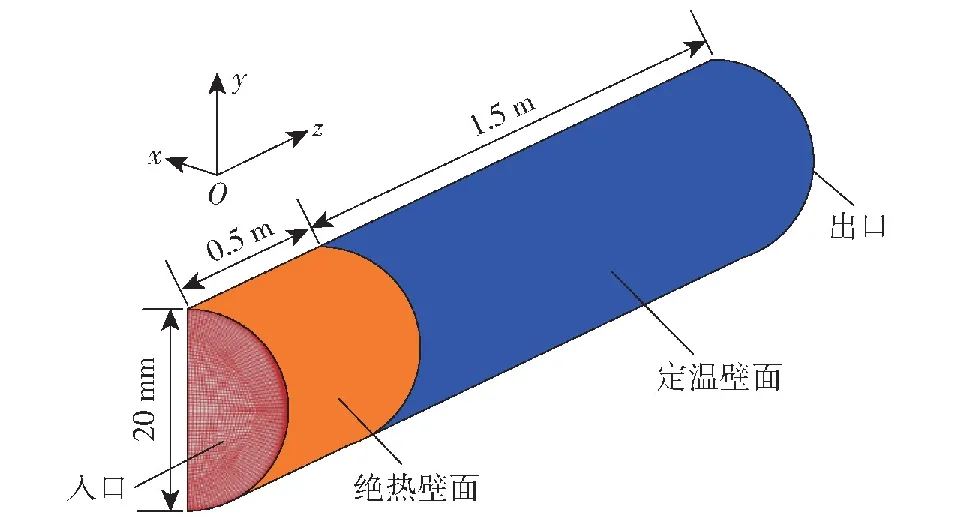
图5 换热器管道流域示意图

在计算中,采用质量流量入口与压力出口的边界条件。考虑到本文主要讨论乏气通道中含不凝气体的蒸汽凝结特性,为便于计算分析,在壁面条件方面,将前0.5 m的管道侧壁面设为绝热壁面,之后的侧壁面设置为恒壁温。根据表1中HAP三组元燃料的燃气组分,将燃气成分设定为水蒸气与CO2,且不考虑CO2的溶解度。根据实际工况,相关的边界条件设置如表3所示,由于模型只有半域,设定的入口质量流量为理论值(20 g/s)的一半。在计算过程中考虑了重力的影响。

表3 仿真计算的边界条件

1.4 模型验证

1.4.1 试验验证

运用试验装置进行高压换热器试验,得到试验的工况参数如表4所示。由于试验燃气温度很高,在冷却水通道的后段,冷却水汽化为蒸汽。

表4 试验工况参数

根据试验工况,运用1.1节的数值方法建立套管换热器的数值模型,如图6所示,贴近固体壁面第1层网格高度为0.000 5 mm以保证y+小于1,出入口处第1层网格高度为1 mm,网格渐变因子为1.2。数值模型中将固体壁面材料设置为304 L不锈钢,其导热系数为15 W/(m2·K),比热容为500 J/(kg·K)。

图6 高温热交换器的流域示意图

图7所示为试验与仿真中燃气通道和冷却水通道的温度随换热器长度的分布对比,对试验值加入了标准不确定度误差条。由于管内温度的建立与传感器示数的稳定均需要一定时间,本文试验所得的温度值均采用单次测量方法,误差主要由仪器精度决定,其标准不确定度可计算为

图7 仿真计算与试验的管内温度分布对比

(9)

式中:α为由传感器精度计算得到的误差区间半宽度;k为置信因子,取1.73。

由图7可以发现,在燃气通道与冷却水通道中,数值仿真与试验研究所得的温度分布规律基本相同,但仿真计算的温度数值偏大,两者的相对误差在燃气通道出口处达到了19.5%。相比管内温度,由仪器精度带来的测量误差非常小,其最大标准不确定度仅4.62 ℃,不是数值计算与试验结果差异的主要来源。两者的误差主要是由换热通道的散热造成的,试验用换热器虽然外部包覆了隔热材料,但由于试验温度很高,管道向外界环境的能量耗散无法避免,在数值仿真中对换热器外壁采用了绝热壁面条件,未考虑散热,导致仿真温度值高于试验值。分别对比燃气通道和冷却水通道的温度,可以发现仿真与试验结果在燃气通道的偏差更大,这是因为燃气的比热容小于冷却水,因此管内的能量耗散会导致其更大的温度偏差。

总之,本文建立的仿真方法在预测高压条件下含不凝气体的蒸汽冷凝换热的精度是可以接受的,可用于进行管内含不凝气体的蒸汽凝结特性研究。

1.4.2 网格无关性研究

本文采用结构化网格对计算模型进行网格划分,对于管道截面使用O-block网格划分技术以保证质量。为选择最佳的网格数,本文对数量分别为242万(网格1)、389万(网格2)和627万(网格3)的计算网格进行无关性分析,不同工况下网格节点数量的增长比例为1.6倍。为了同时考虑近壁面网格的影响,3个工况下贴近壁面的第1层网格厚度分别取0.012 mm、0.01 mm和0.008 mm,对应的平均y+数值分别为1.09、0.92和0.86,各工况下径向网格的增长率均取1.2,以保证边界层网格的数量。表5展示了各工况下的计算网格设置参数。

表5 网格无关性研究中各工况计算网格设置参数

计算得到三套网格中壁面底端液膜厚度和对流换热系数(HTC,可按式(10)计算)沿混合气体流动方向的分布规律分别如图8(a)和图8(b)所示,可见三套网格在计算液膜厚度方面误差很小,在计算对流换热系数方面呈现出相同的变化规律,仅在流体刚流出绝热段时有所不同,其中网格1计算得到的对流换热系数存在波动。考虑计算精度和计算成本的要求,本文最终选择网格数量为389万的第2套网格进行后续的数值仿真计算。

图8 网格无关性研究中的液膜厚度与换热系数对比

(10)

式中:Q为圆管底端固体壁面的热流密度;Tb为主流区混合气体的平均温度;Tw为壁面温度。

2 结果与讨论

2.1 换热特性

运用第1节的数值模型与参数设置进行计算,待进出口参数守恒后认为计算收敛。以z轴坐标分别为1.0 m、1.2 m、1.4 m和1.6 m的管道截面为分析对象,获得其对称面处轴向与径向速度沿竖直方向的径向分布,如图9所示。沿管长方向,工质在z=1.6 m处的流速相比z=1.2 m时降低了约0.4 m/s,沿半径方向则降低了约10 mm/s,这是因为在流动中,蒸汽不断在壁面处遇冷凝结,使工质质量逐渐减少,同时管内压力变化很小,因此为保证质量连续,工质流速逐步降低。图9所示的工质速度分布具有不对称特性,其轴向速度呈现上大下小的规律,而径向速度全部为正值,意味着在管道对称面处,工质拥有垂直向上流动的分速度。在y取值为-6 mm～-10 mm的区间中,工质流速显著低于其他区间,该区间处于凝结液膜中,可见液膜流速显著慢于气体流速。

图9 换热器管道中z取值分别为1.0 m、1.2 m、1.4 m和1.6 m处的速度分布

图10(a)展示了管内气-液交界面(气相体积分数为0.5的界面)在对称面上的分布,可以发现,重力的影响十分明显,管道底端的液膜厚度远大于顶端,且沿流向逐渐变厚;对于顶端液膜,其厚度沿流向逐渐减小,这是因为重力作用下顶部凝结流体不断沿壁面流至底部导致的。图10(b)展示了z分别取值为1.0 m、1.2 m、1.4 m和1.6 m截面中的液相体积分数-流线云图,从中可以清晰地发现液膜非均匀分布的现象,同时在气相和液相流体中均存在二次旋流。由于液相工质主要存在于管道下部,气体主要在管道上部液膜较薄的部位进行换热凝结,造成了蒸汽浓度在管道上部壁面附近较低、在管内中心与下部较高的不平衡现象,为此蒸汽由高浓度区域向低浓度区域扩散。另外,工质于管道上部壁面处放热降温,密度增大,由重力作用下沉至管道下部,而此处的高温低密度工质则由于浮力的作用从管道中心区域上浮至管道上部进行放热。在上述因素的作用下,气相工质在管内产生二次旋流,同时流动的气相工质也会带动液相产生垂直于轴向的旋流。

图10 换热器管道的液膜厚度和z=1.0 m、1.2 m、1.4 m和1.6 m处的液相体积分数-流线图

图11(a)和图11(b)分别展示了管道顶端与底端热流密度与壁面换热系数沿管长方向的变化。沿管长方向,主流温度与壁面温度的温差逐渐下降,蒸汽浓度也逐渐下降,使凝结换热强度沿管长方向逐步降低,最终导致热流密度沿流向的下降。由于管道顶部液膜厚度远小于底部,换热热阻较小,是换热的主要发生方向,顶部的热流密度远大于底部。对于对流换热系数而言,随着工质的流动,蒸汽逐渐凝结,浓度逐渐降低,导致凝结换热强度逐渐降低,因此管道顶部换热系数逐渐降低;对于底部,由于液膜厚度较大,致使其具有较大的热阻,不是凝结换热的主要发生方向,因此其换热系数总体较小,且凝结换热强度的变化对其数值的影响不大。

图11 热流密度和换热系数沿换热器管道的轴向变化

总体而言,在水平管道内,由于重力的影响,凝结液体主要集中于管道下部,致使蒸汽凝结换热主要发生在管道上部;蒸汽的凝结导致管内各截面处蒸汽浓度分布不均匀,为平衡浓度,产生了垂直于管长方向的环状二次旋流;沿管长方向,温差与蒸汽浓度逐渐降低,致使凝结换热强度逐渐减弱,导致了热流密度与换热系数的逐步降低,而由于管道顶部液膜较薄,是换热的主要发生方向,顶部热流密度与换热系数均大于底部。

2.2 管径的影响

作为运用于水下动力装置的换热设备,本换热器需要在较小的体积内实现大功率换热,换热管径对含不凝气体蒸汽换热的影响值得进一步讨论。运用表3的参数,分别对圆管半径为10 mm、8 mm、6 mm和 5 mm的工况进行数值仿真,各管径下通道的长径比分别为75、73.75、125和150。

各工况下管内主流温度沿工质流向的变化如图12(a)所示,随管径减小,主流温度下降幅度显著增加,半径5 mm时出口温度为548 K,相比半径10 mm 的工况下降了约6 K,可见管径的减小增加了管道的换热性能,这也体现在热流密度的变化上。图12(b)展示了各工况下管道顶部和底部的热流密度,随管径减小,壁面的热流密度逐渐上升,半径 5 mm 工况的最大热流密度已接近450 kW/m2。对比底部与顶部的热流密度变化,顶部热流密度沿流向的下降趋势随管径减小而越发明显,对于半径 10 mm 和8 mm的工况,顶部热流密度几乎全程高于底部;对于半径6 mm和5 mm工况,进入管道换热段后,顶部热流密度快速下降,并很快降低至小于底部热流密度的水平。

图12 变管径工况下主流温度与热流密度的变化

管道换热性能的变化由工质流速、液膜形态等因素决定。图13(a)和图13(b)分别展示了变管径工况下z=1.2 m处工质的轴向与径向速度分布,为便于比较,对径向坐标进行了无量纲化处理。随管径的减小,管道截面积逐步缩小,导致工质的轴向流速加快,半径5 mm工况下工质在z=1.2 m处的最大轴向流速超过3.5 m/s。增大的轴向流速削弱了重力和浮力的影响,反映在流动上,就是小管径工况的径向流速减小,二次旋流减弱。

图13 变管径工况下z=1.2 m处速度分布

图14展示了各工况下的液膜厚度变化情况。管道底端液膜厚度随管径的减小而逐渐变薄,这是因为液膜的流动主要由气体工质带动,随管径的减小,增大的气体工质流动速度对液膜的剪切作用增加,导致液膜的流速增大,厚度逐渐减小。对于管道顶端的液膜,其在管道前段的厚度随管径减小而增大,且最大厚度位置逐渐延后,在管道后端的厚度则基本不随管径变化。这是因为在管道前段,重力导致的液相滑落效应不明显,液体逐渐在管道上部累积,随管径减小,气体工质流速增加,对液膜的剪切作用增强,因此顶部液膜最大厚度位置延后,液膜厚度也由于液体累积量的增大而变大。在管道后段,重力的作用逐渐显现,绝大部分顶部液体流向底部,因此顶部液膜厚度基本不随管径变化。

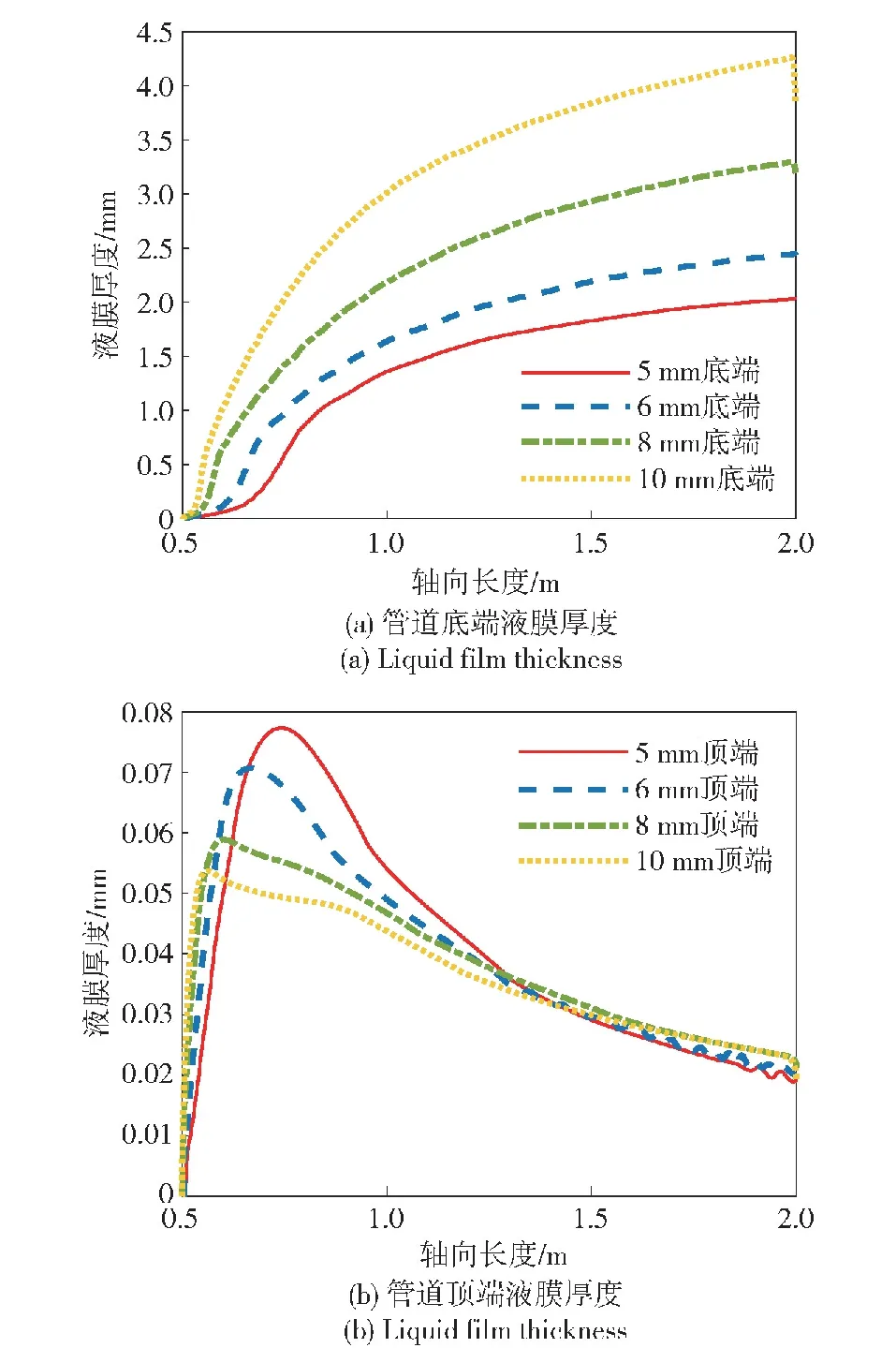
图14 变管径工况管道液膜厚度

在水平管道中,冷凝换热的过程是:蒸汽扩散至气-液界面处冷凝并向液膜放热,液膜中的液相工质将热量传导至管道壁面,并向低温壁面放热。若考虑重力和浮力的影响,管道内所产生的二次旋流将使大部分蒸汽在管道上部冷凝,导致管道上部的冷凝换热量远大于管道下部。然而,随着管道上部的凝结液相工质滑落至管道下部,其一方面使下部液膜增厚,进一步阻碍气体的凝结换热,另一方面也将一部分热量从管道上部传递至下部,平衡了管道上下的换热量差异。在大管径工况下,重力与浮力的作用十分明显,因此管道顶部的热流密度均大于底部。随着管径减小,底部液膜变薄,削弱了液侧热阻,又由于流速增大,削弱了重力和浮力的影响,导致二次旋流强度减弱,管道上部和下部的冷凝换热强度差异减小,而液相滑落导致的热量交换强度基本不受影响。因此,管道顶部和底部的热流密度差距减小,直至小于6 mm后,在换热过程的后段,管道顶部的热流密度小于底部。

在凝结换热过程中,蒸汽冷凝会导致液膜厚度、气相物性与流速等的变化,进而改变管内气相工质雷诺数,而管径变化也会通过影响流速与换热特性的方式改变管内雷诺数分布。图15展示了不同管径工况下管道截面气相主流平均雷诺数与壁面平均热流密度的关系。在各工况下,主流平均雷诺数增加表示流速提升,此时管内工质剪切效应越发显著,有利于增强换热。但对比不同管径工况,可发现在同一雷诺数下大管径工况具有更高的壁面平均热流密度,这是由重力效应导致的。大管径工况中流速更小,重力导致的二次旋流和液相滑落更为显著,有助于削弱热阻,强化换热。而在雷诺数较高的区域,较大的流动剪切作用使重力的影响被削弱,此时大管径工况的壁面热流密度值逐渐向小管径工况靠拢。

图15 变管径工况气相主流平均雷诺数与壁面平均热流密度的关系

换热器要在有限的空间内实现大功率换热,就需要综合考虑换热强度与换热面积。图16考虑了管道的换热面积,展示了不同管径下管道的总换热功率。随着管径的减小,管道总换热面积减小,但由于壁面热流密度的增加,总换热功率仍略有增大。

图16 不同管径管道总换热功率

总之,对比不同管径工况下管道的换热性能,可以发现较小的管径使工质流速增加,有助于加强换热,虽然减小管径会导致总换热面积的减小,但小管径管道的换热性能仍略强于大管径管道。可见,在本文讨论的工况下,适当降低管径有助于强化换热。

3 结论

本文建立了换热器乏气通道的数值模型,研究了重力条件下含不凝气体的蒸汽冷凝换热特性,分析了管径对换热特性的影响;搭建了高压套管式换热器试验平台,进行了验证试验。得出主要结论如下:

1) 重力对管内换热具有较大影响,一方面管道顶部的液相由于重力滑落,导致顶部与底部液膜厚度不均匀,同时液相质量的转移也会导致一部分热量从管道顶部转移至底部;另一方面,由于管内气相工质密度不均匀造成的管道中部浮力效应,结合管道外部的重力效应,会导致管内气相工质产生二次旋流。上述两种作用导致管壁换热强度的不均匀,管道上部液膜较薄,是换热的主要发生方向。

2) 随着管径的减小,工质流速增加,这一方面增大了雷诺数,另一方面使底部液膜变薄,有助于强化换热;流速的增加削弱了重力的影响,致使管内二次旋流效果减弱,同时结合液膜厚度的变化,导致管道顶部和底部的热流密度差距减小;管道的总体换热能力需要综合考虑换热强度与换热面积,在本文讨论的工况下,减小管径可提升管内换热强度,尽管会导致总换热面积减小,仍有助于强化换热。

3) 对比试验与仿真结果,两者在燃气通道与蒸汽通道的温度变化规律上趋势一致,但试验所得温度值较低,这是因为试验管道向外界的热量耗散导致的。对比结果表明本文所采用的仿真方法是适用的。

本文仍存在一些未尽之处,例如试验中的燃气物性与数值研究中的有所不同,另外数值模型仅考虑了乏气流道,而忽略了海水流道。在后续研究中,将改善试验条件,使试验燃气的物性更贴合实际工况,以获得更为完善的试验数据;在数值模型中添加海水流道,研究乏气与冷却海水在换热过程中的耦合关系。