金属基体复合材料圆锥壳的材料参数识别及动力学敏感性研究

王珺瑶，陈红永，石先杰，左朋,3

（1.中国工程物理研究院总体工程研究所，四川 绵阳 621999；2.工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621999；3.中国科学技术大学 近代力学系，合肥 230026）

轻质高强度的铝合金常被应用于受力构件以保证结构的刚度和强度[1-3]，但是铝合金无法承受过高的温度，而酚醛树脂基纤维增强材料具有耐烧蚀性能适中、物理力学性能良好、工艺性好、成本低等优点[4]，常用于抗烧蚀、热防护结构[5-6]。因此，铝合金-环氧胶-碳酚醛多层结构是一种性能优良的飞行器蒙皮材料结构。飞行器的稳定性和可靠性取决于多层复合蒙皮结构的动力学性能[7]，而复合结构的力学性能由其材料参数决定，因而获得实时准确的复合材料参数对飞行器动力学建模及力学性能预示至关重要。

金属基体-碳酚醛结构是典型的各向同性-正交各向异性材料的多层复合结构，中间胶层保证了界面之间的变形协调及结合强度。对于此类多材料的复杂结构，其中的碳酚醛复合材料受到工艺过程的影响，难以通过传统的单一材料实验获得准确的建模参数，而实验与数值方法相结合的参数识别技术，能够针对多材料的复杂结构获取准确的材料参数[8]。针对单一复合材料组成的结构参数识别方法研究较多，如基于边界位移的有限元更新法的复合材料层合板材料参数识别[9]，基于人工蜂群算法的复合材料层间内聚力模型参数识别[10]，基于桥联模型的复合材料单向板和轴向性能反演识别纤维横向性能及集体性能[11]，以及采用遗传算法和序列二次规划法的车用复合材料的材料参数识别[12]等研究。考虑各向同性-正交各向异性多种材料构成的复合结构，对其中复合材料参数进行参数识别还未见深入研究报道，而且单层复合材料参数识别多基于大量的解析模型计算或有限元分析[13]，结合模态实验[14]等方式获得结构的动力学特性，以此作为参数识别的优化目标[15-16]，可以进行复合材料单层板的参数识别。随着结构复杂度的上升，动力学模型计算量会大幅增加，而基于代理模型[17]的模型降阶技术建立材料参数与动力学特性的直接关联模型，在保证精度的前提下提高材料参数识别效率。针对金属基体-环氧胶-碳酚醛组成的多层复合结构，基于代理模型的参数识别技术可高效获取建模参数。

本文通过建立各向同性-正交各向异性材料圆锥壳的动力学模型，开展了铝合金-碳酚醛复合材料圆锥壳模型的模态实验。基于实验结果，联合实验数值仿真分析和代理模型技术，通过在设计空间内选择足够多的样本迭代获得设计的相应特性，并建立响应面优化模型。最后，应用多项式算法对响应面模型进行多目标优化，获得铝合金-碳纤维复合材料中碳纤维复合材料单层板的9 个材料参数，并研究了圆锥壳前5 组固有频率对材料参数的敏感性。

1 多层复合圆锥壳结构动力学模型

典型金属基体-碳酚醛多层复合圆锥壳结构如图1 所示。在结构中面z=0 处建立正交坐标系(x,θ,z)，x为圆锥壳的母线方向，θ和z分别为圆周和厚度方向，圆锥壳体的母线长度、厚度以及半顶角分别用符号L、h、α来描述，R0和R1分别为圆锥壳的小圆半径和大圆半径。参考给定的坐标系，根据一阶剪切变形理论，圆锥壳上任一点沿x、θ、z方向的变形量U、V、W的矢量形式为，可以由结构中面处的位移分量u=(u,v,w,ψx,ψθ)表示[18-20]：

式中：u、v、w分别为对应点在x、θ、z方向上的线性位移分量；ψx、ψθ分别为绕x、θ方向的旋转位移；t为时间分量。结构中面处的膜应变、曲率变化率和横向切应变可以由位移分量描述[18-20]：

式中：B=xsinα、Rθ=xtanα分别为θ方向的拉梅常数及曲率半径。

在材料本构方面，将铝合金和环氧胶看作特殊的正交各向异性材料单层板处理。根据广义胡克定律，铝合金-环氧胶-碳酚醛复合材料层合板任意第k层的应力-应变关系[19]如式（5）所示。材料铺设顺序为铝合金（k=1）、环氧胶（k=2）、碳酚醛单层板（k≥3）。

根据坐标转换关系T[19]，层合板刚度系数和材料常数Qij间的关系为：。任意一层材料常数的具体表达式为：

式中：E11、E22和E33分别为正交各向异性材料的3 个弹性模量；G12、G23和G13为剪切模量；ijν为泊松比。k=1 和k=2 时，该层材料为各向同性，有和等 2 个独立的材料参数，；k≥3 时，该层材料为正交各向异性，有E11、E22、E33、G12、G23、G13、12ν、ν23和ν13等9个独立的材料参数。

根据建立的本构方程表达式，可得到圆锥壳的动能T和势能U，将圆锥壳的动能和势能代入Lagrange方程，可得：

通过数值求解方程矩阵的特征值，即可获得复合圆锥壳结构的固有频率。

从式（4）—（7）中可以看出，3 层结构的材料参数均会影响圆锥壳的动力学特性。对于金属及高聚物等各向均质材料，材料性质较为确定，且不易发生变化，仿真建模参数易通过材料实验获取；而碳酚醛复合材料参数较多，与加工工艺、材料特性及结构构型有关，为获得较为准确的复合材料参数，基于模态实验进行反向识别是一种可行的办法。

2 复合材料圆锥壳模态实验

模态实验是获取结构动力学特性的有效手段。本文研究对象是由3 种材料制成的多层圆锥壳结构，其中内层是作为结构层的铝合金，外层铺设用于隔热的碳酚醛复合材料层合板，2 层结构用环氧胶粘接在一起。圆锥壳母线长度为 553 mm，顶面内直径为285 mm，底面内直径为120 mm，3 层材料从内到外厚度分别为3、1、11 mm，如图2 所示。

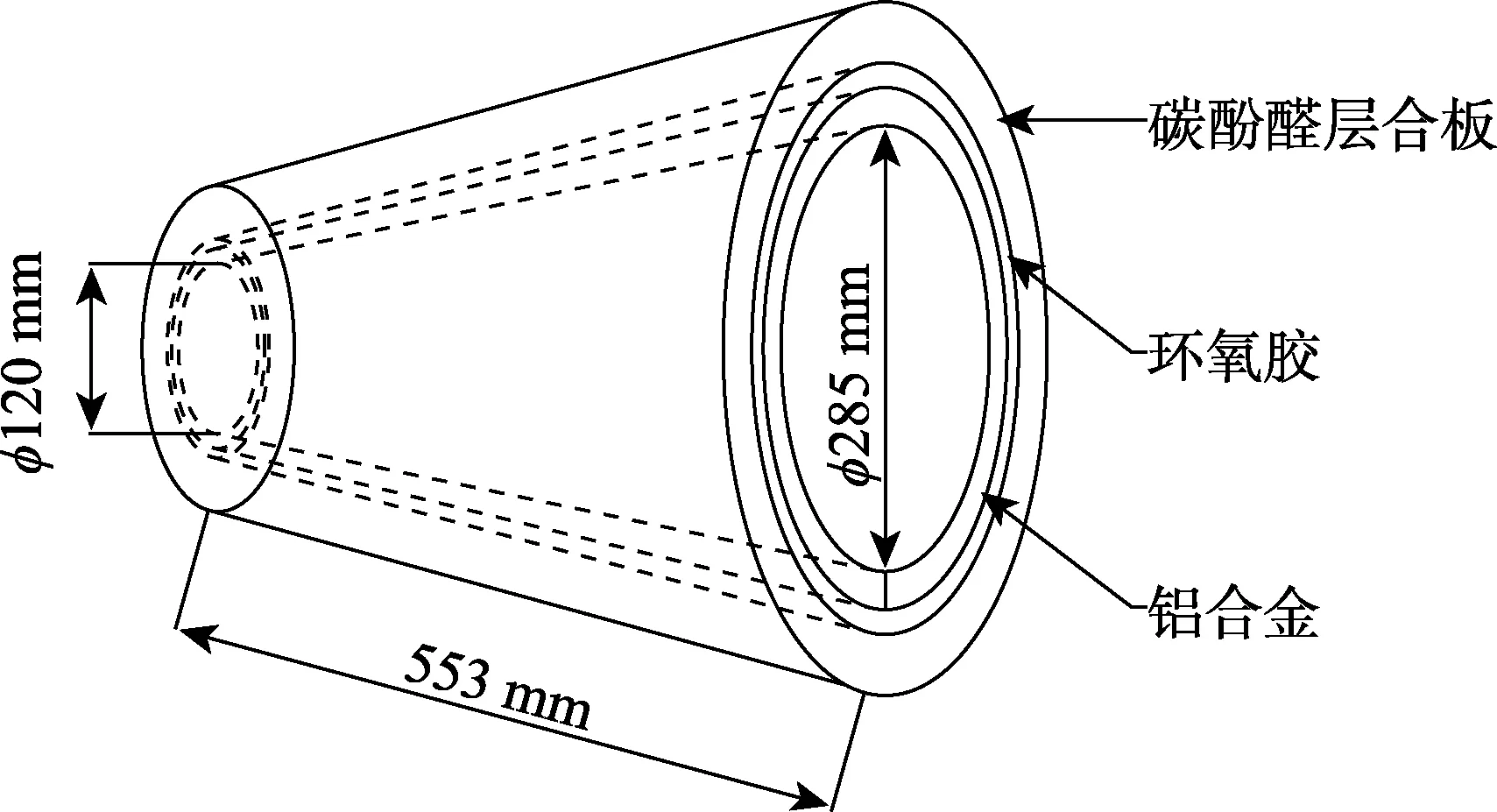
图2 金属基体复合材料圆锥壳试件结构模型Fig.2 Model for specimen structure of metal substrate composite material conical shell

开展复合圆锥壳结构的自由模态实验时，采用低刚度的橡皮绳将圆锥壳大端悬吊，以模拟自由边界条件。圆锥壳模态实验的实验测点布局如图3 所示，沿圆锥壳周向和母线方向分别均布8×5 共计40 个测点。实验采用SIMO 识别方法，测试系统如图4 所示。由于复合圆锥壳低阶模态对结构响应影响较大，且初步分析显示，前10 阶非零频率模态均为对称/反对称模态，每对模态缩并为1 组，取前5 组。通过实验提取前5 组模态结果（见表1），作为参数识别的优化目标。

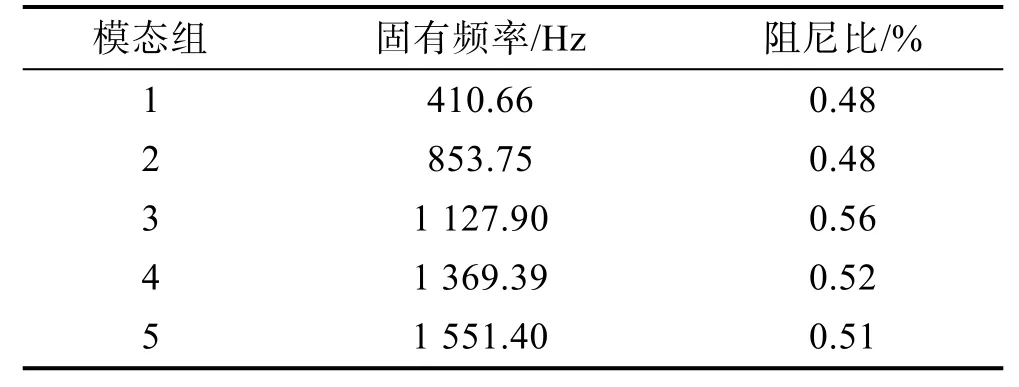
表1 复合材料圆锥壳模态实验前5 组模态及阻尼比Tab.1 Modes and damping ratios of the first five groups of composite conical shell in the modal experiment

图3 圆锥壳自由模态实验及测点布局Fig.3 Free modal experiment of the conical shell and layout of the measurement points: a) free modal experiment of the conical shell; b) layout of the measurement points of the modal experiment

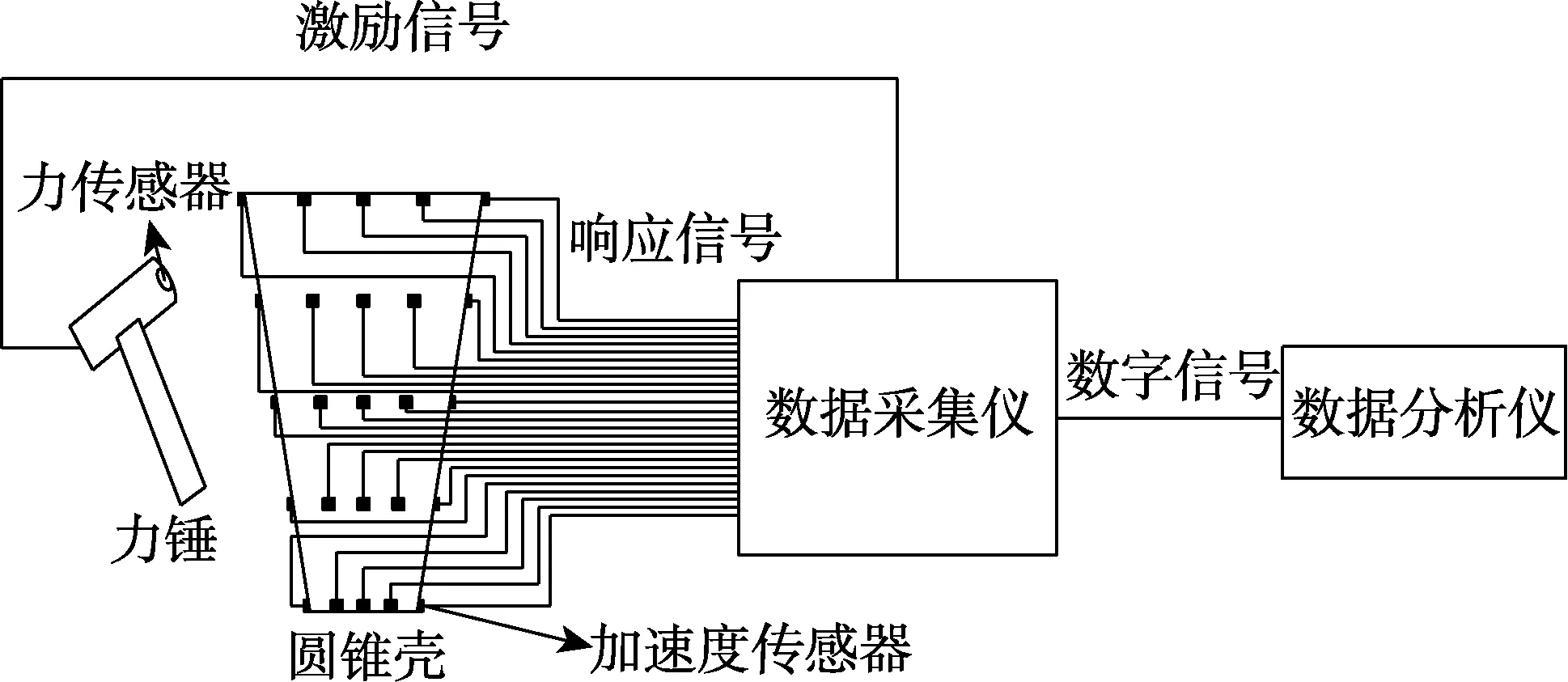
图4 模态实验系统Fig.4 Modal experiment system

3 复合材料参数识别

3.1 圆锥壳动力学代理模型

采用有限元法开展复合圆锥壳结构的模态分析均需开展大量计算，代理模型可以降低计算量，并提高效率。为对参数进行快速优化，需建立复合圆锥壳动力学特性的代理模型，利用近似化的方法对离散的响应数据集合进行插值或拟合化，构建响应面替代实际复杂的仿真计算[21]。

建立试件前5 组固有频率与结构材料参数之间的代理模型时，首先建立试件的动力学仿真模型；其次对材料参数在不确定性范围内抽样取点，仿真获得不同材料参数下复合圆锥壳的固有频率。仿真模型中，采用层合板理论对圆柱壳复合材料层进行建模，根据设计定义碳酚醛复合材料的铺层为[90/0]S。将铝合金及环氧树脂看作各向同性的特殊材料参数的单层板，其材料参数由材料手册获得，密度ρ分别为2 800、1 160 kg/m3，弹性模量E分别为68、3 GPa，泊松比ν分别为0.33、0.3。

建立复合圆锥壳前几阶模态频率与复合材料参数之间的代理模型时，首先建立圆锥壳动力学有限元模型，其几何尺寸与试件保持一致，采用壳单元对复合结构进行建模。经计算，全局网格尺寸为0.02 m时可保证收敛性，边界条件为自由状态。其中铝合金、碳酚醛以及粘接层环氧树脂各层之间采用共节点形式建模，以降低多层界面接触状态差异导致的对结构固有频率的影响。碳酚醛单层板的9 个材料参数均根据工程经验，考虑参数的不确定性区间（见表2），进行初始赋值，并将其作为待识别参数，根据基于响应面优化的参数识别算法进行修正。

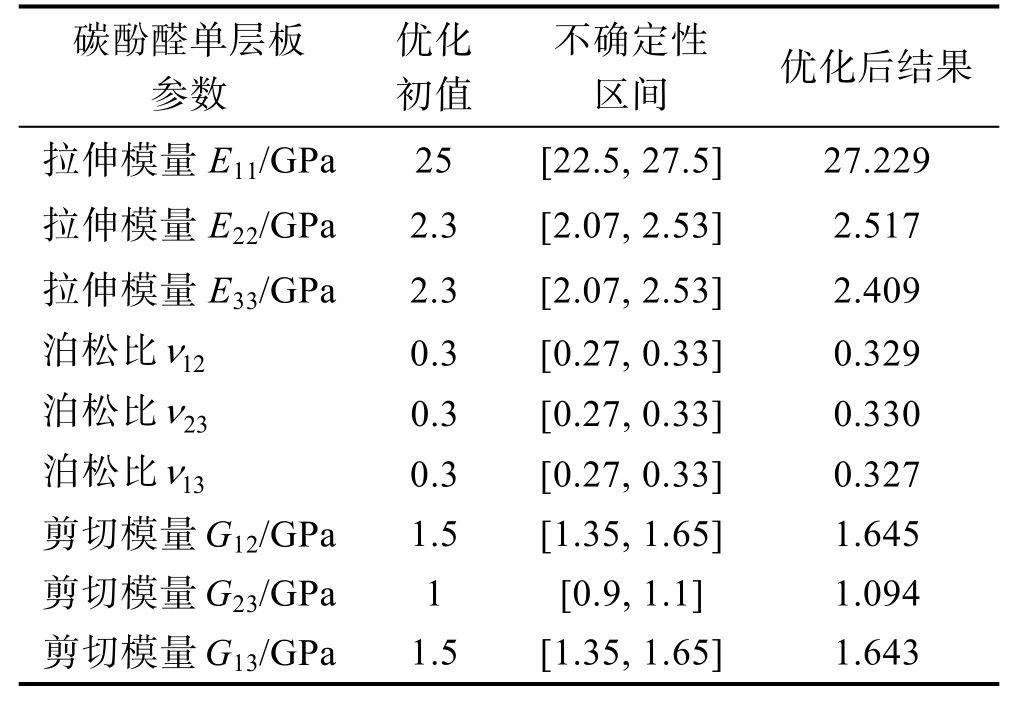
表2 碳酚醛复合材料参数优化结果Tab.2 Material parameter optimization results of the carbon phenolic composite

代理模型的精度依赖于合理、有效的参数采样策略。拉丁超立方法[22]采用特殊的分层抽样方法，能够保证采样点在整个样本空间随机分布、不聚集，且拟合非线性响应能力强，因此本文选择拉丁超立方法为采样方法。完成采样后，采用合适的代理模型对样本点进行数据拟合，构建响应面。多项式响应面是利用拟合原理构造代理模型的方法，通过最小二乘法获得近似多项式的参数建立多项式模型，具有结构简单、计算量小、能够有效过滤计算中的数值噪声等优点，如式（8）所示。

式中：λj代表样本点；表示λj对应的实验第k个固有频率值；ξ0、ξ i、ξ ic是多项式的常数项，通过最小二乘法进行数据拟合求解。

基于代理模型进行参数识别时，考虑工程上在对各阶模态对结构响应影响不明时，假设各阶模态对响应的影响贡献一致，因此取前5 组模态频率平均绝对误差最小进行优化，定义优化函数，如式（9）所示。

式中：m为样本点的个数；为第j个样本点所对应的第l组代理模型的计算频率值。通过仿真建立前5 组模态频率值与9 个材料参数的响应面多项式代理模型，以第1、2 组模态频率的响应面为例，如图5 所示。其中图5 d 给出了复合材料泊松比及剪切模量影响第2 组频率的响应面。

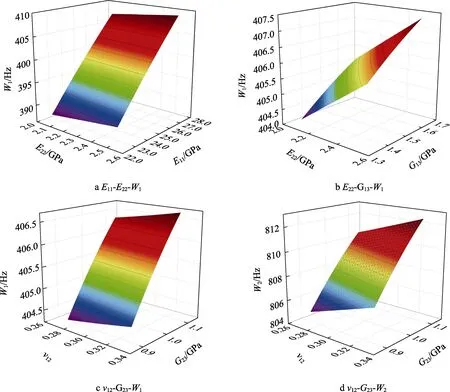
图5 第1、2 组模态频率的响应面Fig.5 Response surface of the 1st and 2nd groups of modal frequencies

从图5 可以看出，在所取值的区间内，第1 组模态频率相对材料参数的响应面线性度较好。可见，随着材料参数变化，频率可能为线性变化。弹性模量对结构固有频率的影响是可以预见的，如式（6）所示，复合材料的泊松比和剪切模量会在不同程度上影响结构复合材料各层的刚度系数，进而对整体结构的刚度矩阵产生影响，最终影响复合圆锥壳结构的固有频率。随着泊松比变大，第2 组模态频率升高；随着剪切模量变大，固有频率也呈上升趋势。第 2组模态频率随剪切模量的变化斜率大于随泊松比的变化斜率。

为保证构建完全多项式代理模型的可靠性，参数优化后，采用均方根误差ηRMSE、决定系数R2等指标评估优化结果[23]，如式（10）和式（11）所示。均方根误差ηRMSE越接近0、决定系数R2越接近最大值1，表明代理模型拟合度越好。

式中：yi和分别为第i个样本的实验值和参数优化后的预测值。

3.2 材料参数优化识别

考虑到复合材料加工工艺等带来的不确定性，在优化初值的基础上，对所有复合材料参数考虑±10%的偏差区间，以此作为材料参数不确定性范围。经过多轮迭代优化后，可以确定碳酚醛单层板的等效材料参数，结果见表2。优化过程中引入最大允许Pareto百分比和收敛稳定性百分比评估收敛性。最大允许Pareto 百分比定义为：每次优化迭代过程中想获得的满足Pareto 最优解的点个数与每次迭代样本点数量之比。收敛稳定性百分比是基于均值和均方差表示全局稳定性的参数，定义如下：

式中：S为收敛稳定性百分比；Wmax、Wmin为初始迭代目标值的最大值和最小值；Ai和Ai-1分别代表第i次和第i-1 次迭代目标值的均值，也可用均方差来计算。优化过程中，设置最大允许Pareto 百分比为70%，收敛稳定性百分比为2%。

参数的收敛性如图6 所示，模型在经过8 次迭代后即可收敛。模型预测结果与实验值的对比如图7 所示，均方根误差ηRMSE均接近0，决定系数R2达到1，表明本文建立的优化代理模型具有较高的准确度和可靠性。从优化结果可以看出，优化后除第2、3 组模态频率误差分别为2.62%和9.94%之外，其他组次均优于1%。

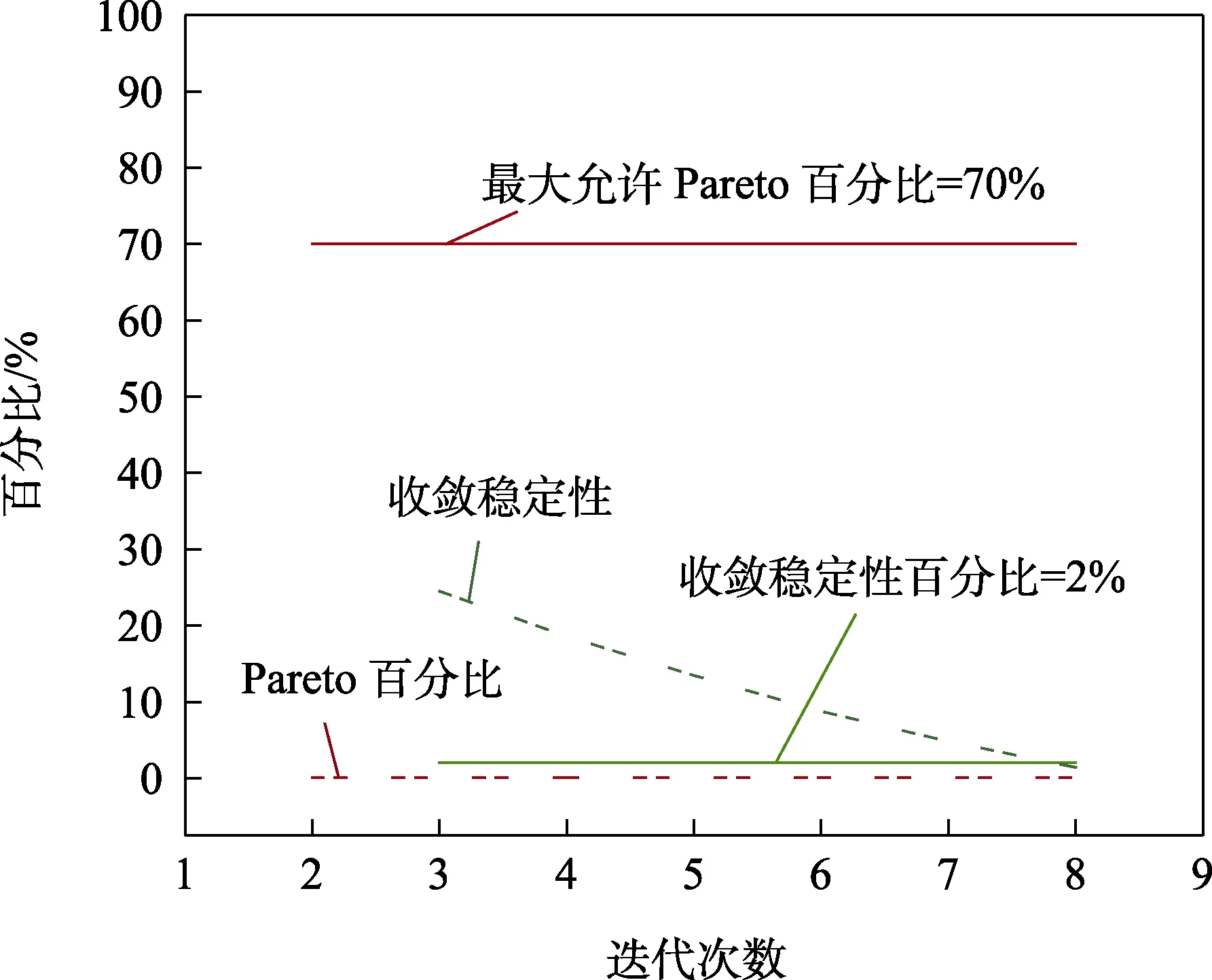
图6 优化结果的收敛性Fig.6 Convergence of optimization results

图7 材料参数优化后试件模态仿真与实验结果对比Fig.7 Comparison between modal simulation results and experimental results of the specimen after optimization of material parameters

4 参数敏感性分析

为分析碳酚醛的各材料参数对圆锥壳动力学特性的影响程度，采用敏感性指标进行表征[24-25]。本文优化变量为碳酚醛单层板的9 个材料参数，通过代理模型分析圆锥壳前5 组模态频率对复合材料参数的敏感性，以前3 组模态频率为例，如图8 所示。

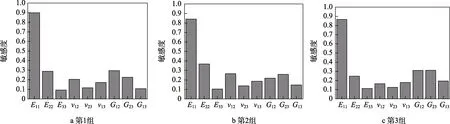
图8 前3 组模态材料参数对复合圆锥壳固有频率敏感性Fig.8 Sensitivity of the first three groups of modal material parameters to the natural frequency of composite conical shells:a) 1st group; b) 2nd group; c) 3rd group

从图8 中可以看出，针对本文中圆锥壳结构的前3 组模态频率，碳酚醛复合材料参数中，纤维方向的拉伸模量E11对固有频率的影响最大，三向拉伸模量中，厚度方向拉伸模量E33的影响最小。3 类参数中，拉伸模量的影响最大，泊松比的影响最小，剪切模量的影响介于拉伸模量及泊松比之间。图8 中也显示出，针对不同组模态频率，各参数的影响程度各不同。敏感性结果可为识别影响复合圆锥壳结构动力学特性的关键参数提供直观的参考。

5 结论

本文基于代理模型方法，建立了针对铝合金-环氧胶-碳酚醛多层复合圆锥壳的材料参数优化识别方法，并分析了圆锥壳结构动力学特性对材料参数的敏感性。主要研究结论如下：

1）基于拉丁超立方抽样及多项式代理模型，可在仿真模型基础上建立精度较好的圆锥壳结构前5组模态频率对复合材料参数的代理模型。

2）通过考虑材料参数不确定性区间，经过参数优化识别之后，复合圆锥壳结构的碳酚醛单层板的结构固有频率与实验值吻合较好，优化后的材料参数可用于进一步结构动力学分析。

3）通过参数敏感性分析可知，铝合金-环氧胶-碳酚醛圆锥壳结构中，碳酚醛单层板E11对固有频率的影响最为显著。

4）与复合材料弹性模量参数影响类似，泊松比和剪切模量等参数也会同时影响复合材料层合板的刚度系数，从而影响复合圆锥壳结构的固有频率。与弹性模量相比，泊松比ν23对前5 组模态频率的影响最小，剪切模量的影响介于拉伸模量及泊松比之间。