经典水跃水气两相流特性的数值模拟

倪诚阳，唐 恋，吕文龙，王 航

(1.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2.长江三峡技术经济发展有限公司，重庆 401120)

1 概述

水跃在上游急流和下游缓流之间存在着流态复杂的旋滚区，通常伴随着大尺度涡流的产生、自由面波动、能量耗散以及大量掺气[1]。河床坡度和粗糙度、过水断面的突然变化或者人工建筑物等各种形式的流动阻力常常在天然河道和水利工程中引发水跃，为了流体混掺或污水处理，水跃也同样被广泛应用在工业加工中。

国内外研究人员针对水跃的流动形态和水气两相流特性开展了大量研究。Hager[2]通过实验观测给出了水跃长度和自由面轮廓的经验描述；Chanson和Brattberg[3]使用电阻式两相流探直接测量水跃的水气两相流特性，提出掺气浓度和水气界面速度的典型垂直分布。刘沛清[4]论述了水跃扩散段内流速分布的理论分析结果，其可靠性通过与实验资料的对比得到了证实；张沁等[5]对多种工况下不同形式的水跃进行实验研究，测量并分析了水跃消能率，建议在实际消能工程中多采用稳定水跃。数值模型可以方便地改变水流和边界条件，并以比物理模型低得多的成本详细显示内部流动结构[6]，因此被广泛用于水工结构设计和明渠流动研究。随着计算能力和水气两相流基础理论的发展，关于水跃的数值研究越来越多地出现。最常用的方法是求解多相形式的雷诺平均Navier-Stokes(RANS)方程、湍流模型以及界面追踪模型。Bayon等[7]对比模拟与实验的水跃自由面轮廓、时均水平速度，评估了两个RANS平台建模水跃的能力。惠康[8]等采用FLUENT软件分析不同坡度对水跃跃长的影响；郑铁刚等[9]通过RANS方法模拟了来流弗劳德数为3.19的淹没水跃，分析内部流场的同时发现水跃旋滚显著影响着紊动的产生和耗散，但对压力分布影响较小；程香菊等[10]使用同样的方法模拟波浪形底板上的水跃，展示了水跃的演变过程、跃长以及流速分布。

掺气浓度和水跃的部分自相似性在水环境领域和工程应用中至关重要，而对此进行的数值研究却很少见。本文基于二维混合模型NEWFLUME[11]对3个来流弗劳德数下的经典水跃进行数值研究，对比了模拟结果与Wang等[12]的实验数据集，包括自由面形态、时均水平速度和掺气浓度分布、以及断面最大流速和掺气浓度的沿程自相似分布，系统地验证了此模型的可靠性。

2 数学控制方程

水利工程中水相和气相的流动速度远小于声速，混掺的气泡和水被视为不可压缩的混合流体，平均运动由雷诺平均Navier-Stokes方程描述，混合模型的连续性方程和动量方程如下：

∇um=0

(1)

(2)

式中，um、ρm、Pm—两相流体的混合速度、密度和压力；g—重力加速度；t—时间；τGm—混合流体的黏性应力张量和湍流应力张量；τDm—气泡和液体相对运动引起的扩散应力张量。

应力张量的表达公式如下：

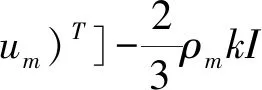
(3)

τDm=-ρmC(1-C)urur

(4)

式中，I—单位张量；k—混合流体的紊动能；C—掺气浓度，定义为每单位体积气-水混合物的气相占比；ur—气泡和水之间的相对速度；νm、νTm—混合流体的运动黏度和运动涡流黏度。

根据每个计算网格的掺气浓度确定混合物的密度和运动黏度，得出：

ρm=ρgC+ρl(1-C)，νm=νgC+νl(1-C)

(5)

式中，ρg、ρl—空气和水的密度；νg、νl—空气和水的运动黏度。

对于气泡在静水中的上浮速度urs，Comolet[13]强调表面张力和浮力的重要性并建议：

(6)

式中，d—气泡的平均直径；σt—空气-水表面张力。

在掺气浓度为C的水气两相流中，气泡上浮速度ur的表达式变为[14]：

(7)

采用标准k-ε湍流模型来模拟水跃的湍流特性，该湍流模型计算成本较低且不易出现收敛问题：

(8)

(9)

(10)

式中，ε—湍动能耗散率；Ps—紊动能生成项。

Ps表达式及方程中的系数设置如下：

Ps=τGm∇um

(11)

Cd=0.09，σk=1.0，σε=1.0，C1ε=1.44，C2ε=1.92

(12)

VOF(流体体积)模型的有效性在广泛的流动建模中得到了证明，在模拟剧烈水气混合现象时，既需要计算水体中掺气浓度的分布，又需要追踪紊动自由面，相较于单相流和存在清晰界面的两相流复杂得多。本研究在传统VOF方法的基础上引入额外的对流项以控制数值耗散并提供分辨率更高的相界面，通过求解该优化后的模型提高运动自由面和掺气浓度的模拟精度[15]：

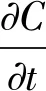
(13)

通过求解方程(13)获得计算域中每个网格单元的掺气浓度，然后根据掺气浓度分布使用二阶精度的Youngs算法重建自由面。Youngs算法允许每个网格中重建的两相界面为斜线，而不局限为垂线或者水平线，可以有效减少数值耗散、数值色散性和不稳定性，从而更准确地获得贴合实验现象的清晰自由面[16]。

3 物理模型及算例设置

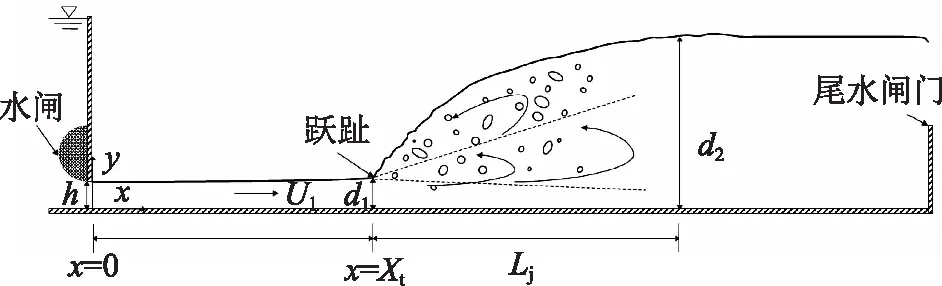
Wang等[12]发表于2015年的论文描述了一组经典水跃实验。横断面为矩形的水平平底水槽，其长3.2m，宽0.5m，深0.41m，由光滑的高密度聚乙烯底板和玻璃侧壁构成。上游高位水箱具有恒定水头，通过半圆形水闸形成水平入流。对于给定的流量，调节渠道末端尾水闸门的高度改变下游水位，从而控制水跃的发生位置。实验装置示意图及相关符号如图1所示，图1中x是自闸门进口处沿入流方向的水平坐标，y是自渠道底板向上的垂直坐标。固定上游闸门开度h=0.03m，跃趾位于纵向位置Xt=1.25m。水跃的来流边界层厚度δ

表1 实验流动条件总结

图1 经典水跃模型实验概化图

如图2所示，实验使用多个超声测距仪(ADMs)测量水跃自由面高程，并使用双针的电阻式两相流探针(PDPs)测量水气两相流特性。超声测距仪朝向检测水面，发射声束并接收水面反射的声束，由声束行进时间获得传感头与被检测水面之间的距离。固定于中心线上的探针有两个平行但长度不同的针式传感器，正对来流方向。探针信号是与内部电极导电率成比例的电压样本，根据电压变化来区分气相和水相。采用气相和水相电压水平之和的50%为临界值对信号进行二值化处理，其中0代表水，1代表空气，从而获得时均掺气浓度。两个传感器的原始信号之间的互相关分析进一步提供气泡-水界面的水平速度。

图2 水跃实验中的仪器

二维计算域与水槽长度相同，高度大于跃后水深。在计算域左边界的闸门出口处设定与实验条件相同的均匀水平速度，对固边界施加无滑移条件，在计算域右边界的过冲闸门处施加自由出流条件，对自由面边界施加零剪应力条件。边界层内的湍流发展未被解析，固边界附近的湍流场用壁面函数处理。

计算域被离散为统一尺寸的网格系统，采用4种不同尺寸的网格进行收敛性分析。网格的长和高(Δx×Δy)分别为0.025m×0.003m、0.03m×0.004m、0.03m×0.005m、0.035m×0.005m，最大与最小网格尺寸的比值大于1.3，满足Celik等[17]的建议。选取Fr1=5.1水跃的掺气浓度分布作为收敛指标，图3比较了相对位置(x-Xt)/d1=11.6处的模拟与实验结果。同时断面平均掺气浓度Cmean的相对误差在表2中显示，为满足相对误差小于10%的要求[18]，采用0.025m×0.003m的网格尺寸。本文根据实验经验采用45s的模拟时长，以确保特征变量的收敛。

表2 模拟的断面平均掺气浓度与实验结果的相对误差

图3 使用不同尺寸网格模拟的掺气浓度分布与实验数据的比较

4 模拟结果与分析

4.1 水跃形态

经典水跃共轭水深比d2/d1的理论关系式：

(14)

如图4所示，模拟得到的弗劳德数为3.8、5.1和7.5水跃的共轭水深比分别为4.95、6.62和9.97，此结果与公式(14)的比较显示出良好的一致性。模拟的无量纲水跃长度Lj/d1分别为18.7、27.0和45.2，共轭水深比和水跃长度的模拟结果与实验值的相对误差均小于3%。水跃消能率与共轭水深比密切相关，所以能够预见本模型对经典水跃消能率的准确预测。

在水跃长度范围内(0<(x-Xt)/Lj<1)，实验测量的自由面形态表现出自相似性[19]：

(15)

式中，η—水跃长度内的时均自由面高程，接近特征高程Y50(掺气浓度C=0.5对应的高程)。

两相流探针还记录了定义掺气水流上边界的Y90(C=0.9对应的高程)，同样具有自相似轮廓[19]：

(16)

从计算域的时均掺气浓度分布中提取模拟的特征高程Y90和Y50。图5将模拟结果与拟合公式进行比较，并计算出Y50和Y90的决定系数分别为R2=0.980、R2=0.984，表明此数值模型能够在模拟时长内准确再现水跃的流动形态。

图5 模拟自由面轮廓和拟合曲线的比较

4.2 时均水平速度

水跃速度场包括渠底上方形成的边界层、湍流剪切层中的正向速度以及自由表面回流区中的负速度。图6对比了3个工况下的时均水平速度的模拟结果和实验值，每个工况包含4个不同位置的垂直截面。注意混合模型的模拟速度是混合流体速度，不区分气相和水相，而两相流探针测量的实验数据反映气泡-水界面的速度，更近似于气泡速度。模拟结果和测量值在高度较低(相对高程0

图6 不同截面上水平速度的模拟与实验结果比较

图7展示了模拟的无量纲最大速度Umax/U1的流向衰减。先前的实验研究表明，在不同流动条件下，Umax/U1在水跃长度范围内遵循相似的衰减曲线，可被方程(17)所拟合[20]，模拟结果与此非常一致。

图7 模拟无量纲最大速度的流向衰减以及与经验公式的比较

(17)

4.3 时均掺气浓度

掺气过程是水跃最显著的特征之一，且掺气浓度对于满足生化需氧量、防止空化空蚀破坏、确定水工建筑物的安全超高至关重要。虽然此模型无法模拟单个气泡的形成及动力学过程，但通过追踪宏观水气界面以及截留空气的对流扩散，能够很好地预测水跃的掺气浓度分布。

图8比较了时均掺气浓度分布的模拟与实验结果，在所有流动条件下，掺气浓度及其特征值的分布具有相似性。局部最小掺气浓度将分布曲线清晰地分为两部分，在其下方和上方分别是掺气浓度呈钟形分布的射流剪切区和单调增加的回流区。图8的对比反映模型低估了渠底附近的掺气浓度，模拟的钟形分布较窄，与实验相比，掺气浓度在垂向上的扩散受到了限制。目前的混合模型不能模拟出涡旋结构携带的分散气泡对渠底贡献的掺气浓度，因此需要进一步研究空气扩散模型来改进强掺混过程的建模。模型以较高的精度模拟出掺气浓度在上方回流区的增长趋势，以及由于掺气而导致的水体膨胀效应，虽然实验记录的回流区由于自由面的液滴飞溅而更厚。

图8 不同截面上模拟和实验测量的掺气浓度比较

随着空气的垂向扩散，湍流剪切层中的最大掺气浓度Cmax在流向上减小，其相应高程yCmax随着流动深度的增加而增加。Wang等[20]根据实验数据拟合出它们的变化曲线：

(18)

(19)

图9将模拟的Cmax和yCmax与拟合公式进行了比较。0<(x-Xt)/Lj<0.3时，Cmax的模拟值偏大，归因于模型对垂向扩散系数的低估。总体而言，模型很好地预测了Cmax的指数下降和yCmax的线性增加，并且成功地再现了它们在不同弗劳德数下的自相似性。

图9 掺气浓度分布的自相似性以及与经验公式的比较

5 结语

本文通过NEWFLUME混合模型模拟了3个弗劳德数的经典水跃，凭借模拟结果与实验数据的全面对比得出主要结论如下：

(1)使用RANS方法建模水跃时，不同尺寸的计算网格将得到差异显著的模拟结果，因此网格敏感性分析必不可少。

(2)混合模型可以准确再现水跃的时均自由面轮廓、消能率、基本的水气两相流特性，以及不同弗劳德数下速度和掺气浓度表现出的自相似性。

(3)计算结果与高质量数据的交叉比较对于模型验证和分析各研究方法的可靠性不可或缺。两相流探针在水跃回流区对负速度的测量出现高估，而混合模型会低估湍流剪切层中垂向上的空气扩散速率，需要进一步改进本模型对强水气掺混过程的模拟。