圆锥曲线内接三角形定值定点问题的充要条件

南京市栖霞中学(210046) 刘建国 胡党琴

一、问题背景

笔者在梳理近几年的高考题中,以斜率为背景的定值定点问题在高考中层出不穷, 如2020 年新高考Ⅰ卷第22 题,2021 年新高考Ⅰ卷第21 题,2022 年新高考Ⅰ卷第21 题,2017年全国Ⅰ卷理科第20 题等等,这体现了高考“常考常新”的特点. 笔者在文献[1]中阐述了椭圆与抛物线中相交线的中点弦的定点问题,其中结论6 中,过椭圆上一定点A引两条弦AB,AC,当直线AB,AC的斜率之积或之和为定值时,发现直线BC过定点. 基于结论6,深入探究有关椭圆内接三角形的定值定点问题, 发现在椭圆的内接ΔABC中, 若点A为顶点,ΔABC的三边斜率满足一定的关系时,直线BC过定点,并且这个定点与ΔABC的三边斜率满足的等式关系具有等价性,揭示了圆锥曲线中定值定点问题的内在统一性,进一步丰富了此类问题的内涵.

二、结论探究

结论1已知椭圆A为椭圆C的右顶点, 过点A作直线AM,AN交C于M,N两点, 设直线MN,AM,AN的斜率分别为k,k1,k2,则k(k1+k2) =λ(定值) 的充要条件为直线MN过定点.

图1

图2

图3

三、类比迁移

在上述结论中,得到了两类椭圆内接三角形三边斜率关系(定值)与直线定点问题之间充要条件,在证明过程中,通过构造新的坐标系,将原有的椭圆方程转化为一元二次方程,通过韦达定理构造斜率之积与斜率之和的关系,在证明过程中不难发现,斜率之和与斜率之积都是关于直线方程中的有关参数问题,同样的对于双曲线与抛物线中也有类似的结论.如下所示.

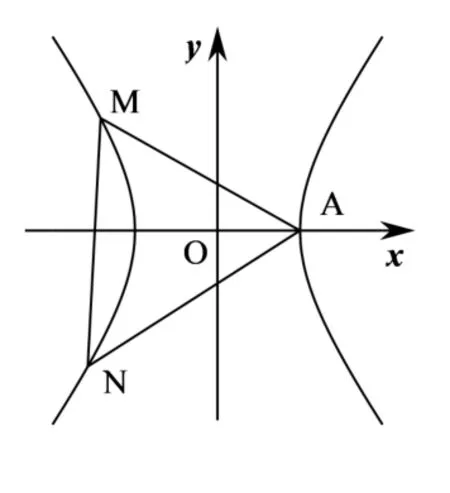
图4

图5

四、结论应用

基于上述椭圆有关的内接三角形的三边斜率关系的等式关系有关直线定点问题的等价性,在一些高考模拟题中均有体现,其本源是来自与高考真题的背景下进一步对问题进行深入研究后的结果,以具体曲线为载体,将相应的条件具体化(赋值)呈现在解题者面前. 笔者罗列了以下两道高考模拟题,供有兴趣的读者进行对比与解答.

五、结束语

圆锥曲线中基于斜率关系的定点定值问题背景下进行命题层出不穷,在一些高考试题与各地模拟试题中时常出现,背景揭示了圆锥曲线中定值定点问题的内在的统一性,问题呈现的形式却是千变万化(如文献[2]). 因此在平时复习备考过程中,教师应注重对此类问题的探究,在问题的基础上拓宽问题的深度与广度,同时也需要教师站在一定的高度审视此类问题的命题背景,只有对问题进行深入探究,才能帮助学生更好的把握问题的本质,在复习过程中帮助学生跳出题海,充分拓宽学生的思维,避免机械刷题.