2023 届广州市一模第12 题背景揭示与拓展

山东省宁阳县复圣中学(271400) 张志刚

1 试题与解答

题目(2023 届广州市一模第12 题)平面内到两个定点距离之积为常数的点的轨迹称为卡西尼卵形线, 它是1675年卡西尼研究土星及其卫星的运行规律时发现的. 已知平面直角坐标系xOy中,M(-2,0),N(2,0), 动点P满足|PM|·|PN|=5,则下列结论正确的是( )

A. 点P的横坐标的取值范围是

B. |OP|的取值范围是[1,3]

C. ΔPMN面积的最大值为

D. |PM|+|PN|的取值范围是

本题通过创设科学的数学情境,考查曲线与方程相关的新定义问题,考查学生在明晰卡西尼卵形线的几何特征基础上,利用坐标法,建立平面直角坐标系并求出其方程,然后通过方程探讨它的几何性质,并解决一些简单的数学问题,考查数学抽象、数学运算、逻辑推理等核心素养.

2 背景揭示

本题命制背景是卡西尼卵形线. 我们知道,平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆,与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线,它们都是以几何基本元素(点)的相互关系为考察对象,以“距离”为纽带,以“运算”为方法,通过“运算中的不变性”发现了曲线的几何特征,给出定义. 那么,平面内与两个定点F1,F2的距离的积等于常数的点的轨迹又是什么?

十七世纪八十年代,法国天文学家卡西尼(Cassini,1625-1712)在研究土星及其卫星的运行规律时就提出了这个问题.深入研究后,卡西尼发现,到两个定点F1,F2的距离之积为常数的点的轨迹是卵形线[1],并把这两个定点叫做卡西尼卵形线的焦点,两焦点间的距离叫做卡西尼卵形线的焦距. 如今,卡西尼卵形线在天文学、航空航天、电磁学等领域有广泛而重要的应用. 在数学中,卵形线也是解析几何研究的一类重要曲线.

3 问题拓展

3.1 范围

3.2 卵半径

3.3 焦点三角形

3.4 离心率

a和c是确定圆锥曲线的基本量,而二者之比即离心率则刻画了圆锥曲线的扁平程度. 由卡西尼卵形线的定义可知,a和c也是确定卡西尼卵形线的基本量,我们不妨把称作卡西尼卵形线的离心率,其大小是否也决定了卡西尼卵形线的形态呢? 我们首先通过GeoGebra 作图,直观感知参数的变化对曲线形状、大小的影响.

如图1 示, 固定c的取值, 随着a从0 开始逐渐增大, 卡西尼卵形线从两定点(焦点F1、F2) (情形1)开始生长,先是分开的两支封闭曲线(情形2),然后变为双纽线(情形3),再融合为一个曲线,而且此曲线由中部凹进(情形4)到中部扁平(情形5)再到中部隆起(情形6),共六种不同形态,详见表1.

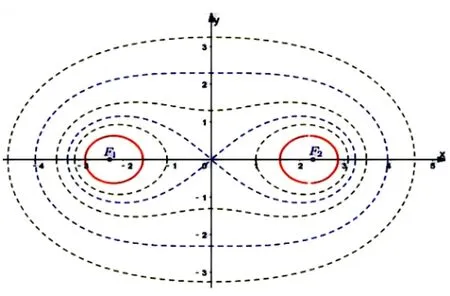
图1

表1 e的取值决定卡西尼卵形线的形态

特殊的,当e= 1 时,卡西尼卵形线即为伯努利双纽线,呈8 字形,它还是是圆的特殊变形,是椭圆的类比与拓展,是等轴双曲线的特殊反演变化,沟通了各曲线之间的联系.

借助卡西尼卵形线的方程,我们还可讨论它的顶点、对称性等几何性质,不再赘述.

4 应用强化

近年,以卡西尼卵形线为背景命制的试题频频在高考或模拟试题中亮相. 题目往往为客观题压轴题,侧重考查卡西尼卵形线的对称性、有界性、卵半径、焦点三角形的面积等性质,承载信息丰富,解法灵动多变,区分度较大,需综合运用函数、方程、不等式放缩等知识求解. 下面举两例说明.

例2(苏州高级中学八校联盟2022-2023 学年高三上学期第二次适应性检测第11 题) 2022 年卡塔尔世界杯会徽(如图2) 正视图近似伯努利双纽线. 在平面直角坐标系xOy中, 把到定点F1(-a,0),F2(a,0) 的距离之积等于常数a2(a＞0)的点的轨迹称为双纽线C. 已知点P(x0,y0)是双纽线C上一点,下列说法中正确的有( )

图2

A. 双纽线C关于原点O中心对称

C. 双纽线C上满足的点P有两个

D. |PO|的最大值是

解显然, 本题中曲线C为伯努利双纽线, 其方程为(x2+y2+a2)2=a4+ 4a2x2, 容易验证说法A,B, D 是正确的. 对于选项C, 若|PF1| = |PF2|, 则点P(x0,y0) 在F1F2的垂直平分线x= 0 上, 联立解得故曲线C上有且仅有一个点(0,0)满足|PF1| = |PF2|,说法C是错误的,故选ABD.

“现代数学强调用代数的方法研究几何问题,其本质是通过几何图形建立直观,通过代数运算刻画规律.”[2]以上类比圆锥曲线的研究过程与经验,围绕“以曲线的不变量表示几何元素或几何关系”的主题,以数形结合思想和坐标法为核心,经历“分析背景—探索几何特征—选择坐标系、建立方程—通过方程研究几何性质”持续连贯的探索过程,完成了对卡西尼卵形线的再认识. 这样的研究过程也表明,利用坐标系建立曲线与方程的关系,是解析几何的基础,而坐标法是数形结合的完美体现,是解决问题的核心和纽带,其处理方法具有程式化的统一性. 事实上,用坐标法解决问题的过程中,引导学生数形结合地看问题,探寻简洁的解题方法并深入思考其原因,就是在解析几何中发展学生直观想象、逻辑推理、数学运算等素养的关键举措[3].