四通阀控非对称液压缸系统控制器优化设计

扈凯 张文毅 祁兵 纪要 李坤

摘要：为优化四通阀控非对称液压缸系统的动态特性，开展控制器优化設计研究。通过AMESim-MATLAB联合仿真的方法开展模型辨识，所构建的传递函数模型的位移误差平均值仅为4.31mm，具有较高的准确度。基于伯德图进行系统的频域分析，结果表明所构建的系统是稳定的，但灵敏度和响应速度较差。设计两种最优PID控制器，基于遗传算法的最优PID控制器响应速度最快，其延迟时间、上升时间和最大超调量分别为0.152s、0.323s和3.43%，基于一阶模型延迟近似的最优PID控制器具有较高的控制精度，其延迟时间、上升时间和最大超调量分别为0.396s、0.438s和0。两种控制器均有效地改善系统的动态特性。

关键词：四通阀控非对称液压缸；控制器优化；模型辨识；遗传算法；最优PID控制器

中图分类号：TH137

文献标识码：A

文章编号：20955553 （2023） 070140

07

Controller optimal design of asymmetric hydraulic cylinder system

controlled by four-way valve

Hu Kai， Zhang Wenyi， Qi Bing， Ji Yao， Li Kun

（Nanjing Institute of Agricultural Mechanization， Ministry of Agriculture and Rural Affairs， Nanjing， 210014， China）

Abstract： A controller optimization design study was carried out in this paper to improve the dynamic characteristics of the asymmetric hydraulic cylinder system controlled by a four-way valve. The model identification was conducted using a joint simulation of AMESim-MATLAB， resulting in a transfer function model with an average displacement error of only 4.31mm， demonstrating high accuracy. The frequency domain characteristics were analyzed based on the Bode diagram. The results showed that the system was stable， but the sensitivity and responding speed were unsatisfactory. Two optimal PID controllers were designed. The optimal PID controller based on the genetic algorithm had the fastest response speed， with delay time， rise time， and maximum overshoot are 0.152s， 0.323s， and 3.43%， respectively. The optimal PID controller based on the first-order delay approximation model had high control accuracy， with delay time， rise time， and maximum overshoot of 0.396s， 0.438s， and 0， respectively. Both designed controllers can effectively improve the dynamic characteristics of the system.

Keywords： asymmetric hydraulic cylinder system controlled by a four-way valve; controller optimization; model identification; genetic algorithm; optimal PID controller

0 引言

四通阀控非对称液压缸是最常见的液压系统之一，被普遍用于以液压缸作为执行元件，需要调速换向的液压回路中［14］，但非对称液压缸在换向过程中，容易产生较大的振荡，造成系统超调量大、响应速度慢、稳定性差等问题［58］。因此，根据四通阀控非对称液压缸的控制模型，构建控制器，优化控制系统的动态响应特性具有积极意义。

近年来，对四通阀控非对称液压缸的相关研究主要集中在控制模型构建、控制方法优化、控制位置精度提高、模型预测等方面［915］。孟亚东等［16］对电液比例对称阀控非对称液压缸的模型开展研究，从工程角度出发，重新定义负载压力、负载流量的概念，推导出对称阀控非对称液压缸两个方向的传递函数。何常玉等［17］提出了一种全新的阀控非对称液压缸位置控制系统自适应鲁棒控制策略，通过引入动态面技术，简化了非线性控制器的设计过程，利用Lyapunov稳定性理论对闭环系统的稳定性进行了分析，控制策略有效地提升了系统的跟踪性能。郭庆贺等［18］对基于内模控制的主动悬挂电液伺服作动器位置控制策略开展研究，与传统PID控制相比，内模控制在单位阶跃激励下，响应快速、平稳、无超调，在正弦输入信号的激励下，内模控制的误差更小。综上所述，对四通阀控非对称液压缸控制特性的优化研究主要集中在两个方面：（1）获取精准的传递函数，为控制器优化提供基础;（2）采用智能化的优化算法，提高控制系统的稳定性、快速性和准确性。

通过开展四通阀控非对称液压缸控制器优化设计研究，采用AMESim-MATLAB联合仿真的方式进行模型辨识，获取系统的传递函数，并对传递函数的准确性进行验证。与理论推导方法相比，模型辨识法可以更全面地考虑液压系统中的时变参数，构建的传递函数精度更高。此外，设计基于遗传算法的最优PID控制器和基于一阶模型延迟近似的最优PID控制器，对比分析两种控制器的控制特性，为四通阀控非对称液压缸的动态特性优化提供理论支撑。

1 四通阀控非对称液压缸模型建立

1.1 理论推导

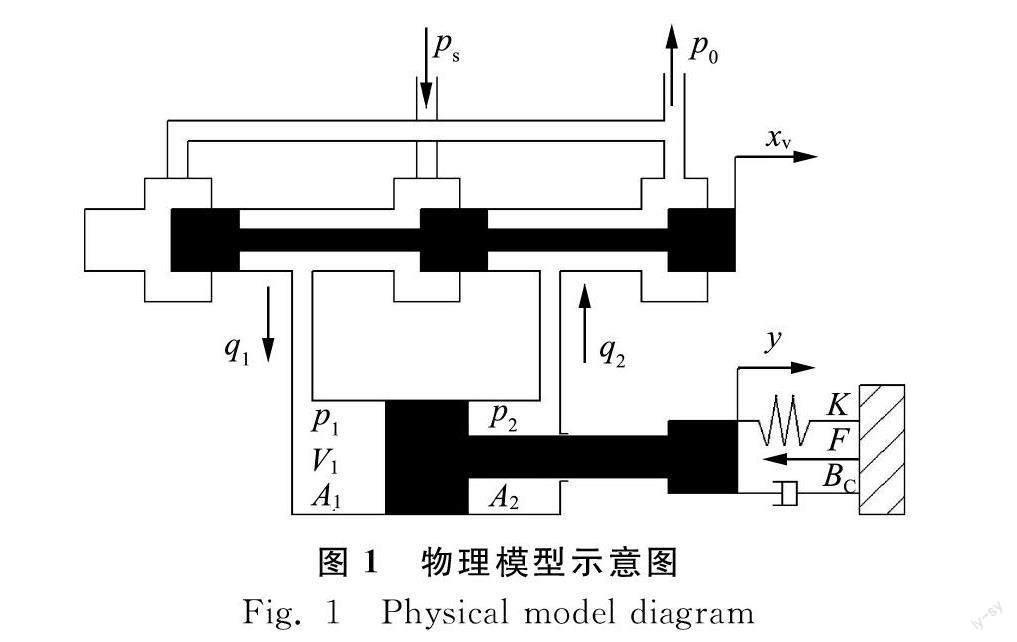
对称四通阀控非对称液压缸的物理模型如图1所示。

在推导系统传递函数的过程中，作如下假设：（1）控制阀为理想的零开口四通滑阀，四个节流口对称；（2）节流口的流动为湍流流动，系统中的流体均不可被压缩；（3）流体在管道内的压力损失忽略不计；（4）流体质量的影响和管道的动态特性可忽略不计；（5）同一联通区域的压力处处相等；（6）油液容积弹性模量为常数。

液压缸稳态时满足力平衡方程和流量连续方程，可知

p1A1-p2A2=F

（1）

q2=nq1

（2）

式中：

p1——无杆腔压力，Pa；

p2——有杆腔压力，Pa；

F——负载力，N；

q1——无杆腔流量，L/min；

q2——有杆腔流量，L/min；

n——无杆腔和有杆腔有效面积比；

A1——无杆腔面积；

A2——有杆腔面积。

负载压力

pL=p1-np2

（3）

根据流体力学方程，液压缸无杆腔流量

q1=cdωxv2ρ（ps-p1）

（4）

液压缸有杆腔流量

q2=cdωxv2ρp2

（5）

式中：

cd——流量常数；

ω——固有频率，rad/s；

xv——比例閥阀芯位移，m；

ρ——液压油密度，kg/m3；

ps——液压泵输出压力，Pa。

当液压缸活塞匀速运动时，可知

q1A1=q2A2

（6）

结合节流方程可知

ps=p2n2+p1

（7）

联立式（3）和式（7）可得

p1=pL+n2ps1+n2

（8）

p2=ps-n2pL1+n2

（9）

结合式（4）～式（9），并由负载流量定义可知

qL=cdωxv2（ps-pL）ρ（1+n2）

（10）

式中：

qL——负载流量，L/min。

根据无杆腔流量连续性方程可知

q1=A1dydt+V01βedp1dt+（Cec+Cic）p1-Cicp2

（11）

式中：

y——液压缸位移，m；

t——时间，s；

V01——

初始时刻无杆腔体积，m3；

βe——有效容积弹性模量；

Cec——液压缸外泄漏系数；

Cic——液压缸内泄漏系数。

根据有杆腔流量连续性方程可知

q2=A2dydt-V02βedp2dt-（Cec+Cic）p2+Cicp1

（12）

式中：

V02——初始时刻有杆腔体积，m3。

根据液压缸力平衡方程可知

A1p1-A2p2=md2ydt2+Bcdydt+Ksy+Fr

（13）

式中：

m——负载质量，kg；

Bc——阻尼系数，N/（m·s）；

Ks——刚度系数，N/m；

Fr——扰动力，N。

将式（10）～式（13）进行拉普拉斯变换，可得比例阀阀芯位移到液压缸活塞位移传递函数的基本形式为

G（s）=Khωh2s（s2+2ζhωhs+ωh2）

（14）

ωh=4βeA2hMVt

（15）

ξh=kfpMβeVt/A1

（16）

式中：

G（s）——

比例阀输入电流到液压缸活塞位移传递函数；

s——传递函数的复数变量；

Kh——系统总系数；

ωh——系统固有频率，rad/s；

ξ——阻尼比；

βe——有效容积弹性模量；

M——系统等效质量，kg；

Vt——系统等效容积，m3；

kfp——流量压力增益系数。

1.2 模型辨识

通常采用解析法构建阀控非对称液压缸的传递函数，但式（14）中的部分参数是时变的［19］，难以准确获取，故本研究通过AMESim-MATLAB联合仿真的方式进行系统模型辨识。在AMESim中构建四通阀控非对称液压缸液压系统模型如图2所示。主要元器件参数设置如表1所示。

在AMESim软件中进行仿真，依次设置草图模式、子模型模式、参数模式和仿真模式，分析类型为线性分析模式，将获取的雅克比文件读入MATLAB进行参数辨识。四通比例阀阀芯位移到液压缸位移传递函数为

G（s）=127.3s2+3.566s2+22 770s

（17）

为验证式（17）的准确性，在AMESim中构建传递函数模型，如图3所示。在阶跃函数的激励下，分别通过传递函数和液压物理模型计算获取液压缸位移曲线和位移误差曲线，计算步长为0.001s，结果如图4所示。

由图4可知，通过传递函数和液压物理模型计算出的位移曲线变化趋势基本一致，在系统到达稳态后，两者误差可以忽略不计。在10s时间内，共有10000个数据点，将所有数据点的位移误差求和除以数据点数量可求取位移误差平均值，将所有数据点的位移误差从小到大排列后，取第5000个和第5001个数据点的平均数为位移误差中位数。经计算可知，位移误差最大值为20.78mm，平均值为4.31mm，中位数为0.25mm。计算数据表明，AMESim-MATLAB联合仿真所获取的传递函数具有较高的精度，可满足控制器的设计要求。

2 动态特性分析

反馈连接的框图如图5所示。

B（s）=C（s）×H（s）

（18）

E（s）

=R（s）-B（s）

=R（s）-C（s）×H（s）

（19）

式中：

B（s）——系統经反馈后的输出；

C（s）——系统输出；

H（s）——反馈传递函数；

E（s）——比较器输出；

R（s）——系统输入。

闭环系统的传递函数

C（s）R（s）=KG（s）1+KG（s）H（s）

（20）

式中：

K——比例增益。

当系统为单位负反馈时，闭环系统的传递函数为

C（s）R（s）=G（s）1+G（s）

（21）

四通阀控非对称液压缸系统为单位负反馈时，式（17）可转换

G（s）=127.3s2+3.566s2+22 770s+127.3

（22）

单位负反馈四通阀控非对称液压缸系统的稳定性开展分析可知，单位负反馈液压系统的幅值裕度为636.84dB，对应的频率为150.89rad/s，相位裕度为180°，对应的频率为0。由系统稳定性判据可知，该四通阀控非对称液压缸系统是稳定的，但相位裕度过大，灵敏性和快速响应能力较差，需要设计控制器对系统的动态性能进行优化。

3 控制器优化设计

3.1 PID控制算法

PID控制是比例—积分—微分控制的简称，由比例系数、积分时间常数和微分时间常数组成，其数学表达式如式（23）所示。

U=Pe+1I∫t0edt+Ddedt+U（0）

（23）

式中：

U——被控制量；

P——比例系数；

I——积分时间常数；

D——微分时间常数；

e——偏差；

U（0）——偏差为0时的被控制量。

其中，比例控制为偏差与比例系数的乘积组成，这是PID控制中最基本的控制量，积分作用与偏差对时间的积分和积分时间有关，加入积分作用后，系统波动加大，但可以消除余差，微分作用与偏差对时间的微分以及微分时间有关，起补偿作用，使系统保持稳定。

3.2 基于遗传算法的最优PID控制器设计

遗传算法是基于进化论，在计算机上模拟生命进化机制而发展起来的一门新学科，根据适者生存、优胜劣汰等自然进化规则来搜索和计算问题的解。遗传算法的求解流程为：（1）选择N个体构成初始种群，并求出种群内所有个体的函数值；（2）设置第1代个体；（3）计算选择函数的值，即通过概率的形式从种群中选择出若干个个体；（4）通过染色体个体基因的复制、交叉、变异等方式创造新的个体，构成新的种群；（5）新种群若不满足终止条件，则重复第3～5步。

在MATLAB中编写遗传算法程序，在SIMULINK中构建系统模型，如图6所示。PID控制器的控制率采用带有滤波作用的一阶环节来表述，如式（24）所示。

Gc（s）=Kp+Kis+Kds0.01s+1

（24）

式中：

Kp——一阶环节比例系数；

Ki——一阶环境积分系数；

Kd——一阶环节微分系数。

选择ITAE指标作为遗传算法的评价指标，ITAE指标可表示为

IITAE=∫∞0t｜e（t）｜dt

（25）

式中：

IITAE——ITAE指标；

t——时间，s；

e（t）——系统误差。

经计算，通过遗传算法获取的最优PID控制器

Gc1（s）=78.41+14.14s+0.52s0.01s+1

（26）

采用该控制器时，液压系统在阶跃函数的激励下的响应曲线如图7所示。

延迟时间定义为响应曲线第一次达到稳定值的50%所需要的时间，上升时间定义为响应曲线从稳态值的10%上升为90%所需要的时间，最大超调量定义为最大峰值与理想稳态值之间的差值，通常用百分数来描述。在AMESim物理模型（图2）中，所计算出来的延迟时间、上升时间和最大超调量分别为0.553s、1.688s和0，而基于遗传算法的最优PID控制器的延迟时间、上升时间和最大超调量分别为0.152s、0.323s和3.43%。基于遗传算法的最优PID控制器使得系统的快速响应能力大幅增加，但原系统无超调，优化后的系统具有较小的超调量。

3.3 基于一阶模型延迟近似的最优PID控制器设计

大部分过程控制的受控对象模型的响应曲线和带有时间延迟的一阶模型非常类似，带有时间延迟的一阶模型可表示

Gc2（s）=kTs+1e-Ls

（27）

式中：

k、T、L——模型的常数系数。

对于式（22）中的传递函数，在MATLAB中编写程序，求取的基于一阶模型延迟近似的最优PID控制器控制率

Gc3（s）=8.41+13.62s+0.853s0.085 3s+1

（28）

采用该控制器时，液压系统在阶跃函数的激励下的响应曲线如图8所示。

基于一阶模型延迟近似的最优PID控制器响应曲线的延迟时间、上升时间和最大超调量分别为0.396s、0.438s和0。与AMESim物理模型相比，基于一阶模型延迟近似的最优PID控制器响应速度更快，延迟时间降低了0.157s，上升时间减少了1.250s。与基于遗传算法获取的最优PID控制器相比，基于一阶模型延迟近似的最优PID控制器响应速度略慢，延迟时间增加了0.244s，上升时间增加了0.115s，但系統超调量为0，提高了控制精度。

4 结论

对四通阀控非对称液压缸控制器优化设计开展了相关研究，通过理论推导和模型辨识的方法构建了准确地控制模型，设计了两种最优PID控制器，优化了系统的控制特性。

1） 通过AMESim-MATLAB联合仿真的方式进行四通阀控非对称液压缸系统的模型辨识，阶跃激励下分别计算传递函数和物理模型的响应曲线，两者之间的位移误差平均值为4.31mm，模型辨识所求取的传递函数具有较高的准确度，可满足控制器的设计要求。

2） 通过伯德图频域特性分析可知，所构建的四通阀控非对称液压缸系统是稳定的，但灵敏度和响应速度较慢，需设计控制器对其动态特性进行优化。

3） 基于遗传算法的最优PID控制器响应速度最快，但存在一定的误差，对应的延迟时间、上升时间和最大超调量分别为0.152s、0.323s和3.43%。基于一阶模型延迟近似的最优PID控制器响应速度较快，系统无超调，对应的延迟时间和上升时间分别为0.396s和0.438s。两种控制器均有效地改善了系统的动态特性。

参 考 文 献

［1］ 彭京， 牛慧峰， 李振宝， 等. 阀控非对称缸全液压转向系统建模与动态性能分析［J］. 机床与液压， 2019， 47（20）： 138-143， 191.

Peng Jing， Niu Huifeng， Li Zhenbao， et al. Modeling and dynamic performance analysis of valve controlled asymmetrical hydraulic cylinder fully hydraulic steering system ［J］. Machine Tool ＆ Hydraulics， 2019， 47（20）： 138-143， 191.

［2］ 孙浩， 陶建峰， 余宏淦， 等. 基于高斯过程的阀控非对称液压缸模型预测控制［J］. 液压与气动， 2021， 45（8）： 26-33.

Sun Hao， Tao Jianfeng， Yu Honggan， et al. A model predictive control method for valve-controlled asymmetric hydraulic cylinders using Gaussian process ［J］. Chinese Hydraulics ＆ Pneumatics， 2021， 45（8）： 26-33.

［3］ 石波， 邓志君， 刘悦， 等. 馈能型多模式主动悬架阻尼力控制策略研究［J］. 中国农机化学报， 2020， 41（7）： 123-129.

Shi Bo， Deng Zhijun， Liu Yue， et al. Research on dam ping force control strategy of multi-mode active suspension with feed energy ［J］. Journal of Chinese Agricultural Mechanization， 2020， 41（7）： 123-129.

［4］ 陈林山. 基于Simulink油气悬架非线性特性影响因素分析［J］. 机床与液压， 2017， 45（19）： 179-184.

Chen Linshan. Analysis on influence factors of nonlinear characteristics of hydro-pneumatic suspension based on Simulink ［J］. Machine Tool & Hydraulics， 2017， 45（19）： 179-184.

［5］ 郑凯锋， 杨桂玲， 房加志， 等. 阀控非对称缸系统的反馈线性化滑模控制［J］. 机床与液压， 2017， 45（5）： 151-154.

Zheng Kaifeng， Yang Guiling， Fang Jiazhi， et al. The control for vale-controlled asymmetrical cylinder based on feedback linearization and sliding mode control ［J］. Machine Tool & Hydraulics， 2017， 45（5）： 151-154.

［6］ 张农， 王少华， 张邦基， 等. 液压互联悬架参数全局灵敏度分析与多目标优化［J］. 湖南大学学报（自然科学版）， 2020， 47（10）： 1-9.

Zhang Nong， Wang Shaohua， Zhang Bangji， et al. Global sensitivity analysis and multi-objective optimization of hydraulically interconnected suspension parameters ［J］. Journal of Hunan University （Natural Sciences）， 2020， 47（10）： 1-9.

［7］ Wen Y， Tan J， Sang Y. Research on fuzzy symmetrical control of valve controlled asymmetric hydraulic cylinder system ［J］. Journal of Intelligent & Fuzzy Systems， 2021， 41（3）： 4451-4460.

［8］ 李净凯， 王敏， 王吉亮， 等. 基于AMESim的4MKJ地膜回收联合作业机开式液压系统设计与试验［J］. 中国农机化学报， 2022， 43（2）： 43-49.

Li Jingkai， Wang Min， Wang Jiliang， et al. Design and test of open type hydraulic system of 4MKJ plastic film recovery combined operation machine base on AMESim ［J］. Journal of Chinese Agricultural Mechanization， 2022， 43（2）： 43-49.

［9］ 王加攀， 吴仁智， 秦磊， 等. 基于AMESim的拖拉机液压提升系统压力冲击研究［J］. 中国农机化学报， 2021， 42（2）： 128-133.

Wang Jiapan， Wu Renzhi， Qin Lei， et al. Research on pressure impact of tractor hydraulic lifting system based on AMESim［J］. Journal of Chinese Agricultural Mechanization， 2021， 42（2）： 128-133.

［10］ Wang H， Leaney P. A new friction model in hybrid pump-controlled asymmetric（single-rod） cylinder drive system ［J］. Tribology Transactions， 2020， 25（2）： 1-14.

［11］ Zhang S， Li S， Minav T. Control and performance analysis of variable speed pump-controlled asymmetric cylinder systems under four-quadrant operation ［J］. Actuators， 2020， 9（4）： 1-18.

［12］ 扈凱， 张文毅. 不同油液体积弹性模量下闭式液压系统动态特性分析及优化［J］. 机床与液压， 2020， 48（16）： 136-139.

Hu Kai， Zhang Wenyi. Analysis and optimization of dynamic characteristics of closed hydraulic system under different bulk elastic modulus of oil ［J］. Machine Tool ＆ Hydraulics， 2020， 48（16）： 136-139.

［13］ 陶翠霞， 赵鹏， 孙波. 多缸液压机的滑模变结构智能同步控制［J］. 锻压技术， 2021， 46（6）： 142-149.

Tao Cuixia， Zhao Peng， Sun Bo. Intelligence synchronous control on sliding mode variable structure for multi-cylinder hydraulic press ［J］. Forging ＆ Stamping Technology， 2021， 46（6）： 142-149.

［14］ 王默， 度红望， 熊伟. 小型救助船舶主动式液压互联悬架系统的设计与仿真［J］. 液压与气动， 2021， 45（8）： 138-144.

Wang Mo， Du Hongwang， Xiong Wei. Design and simulation of active hydraulic interconnected suspension system for small rescue ship ［J］. Chinese Hydraulics & Pneumatics， 2021， 45（8）： 138-144.

［15］ 杨文彬， 胡军科， 王子坡. 闭式液压系统冲洗回路压力平稳性仿真研究［J］. 计算机仿真， 2013， 30（10）： 262-266.

Yang Wenbin， Hu Junke， Wang Zipo. Research on stability of flushing circuit pressure in closed hydraulic system ［J］. Computer Simulation， 2013，  30（10）： 262-266.

［16］ 孟亞东， 杨婉秋， 甘海云， 等. 电液比例对称阀控非对称液压缸的模型研究［J］. 机床与液压， 2020， 48（20）： 54-59， 70.

Meng Yadong， Yang Wanqiu， Gan Haiyun， et al. Study on the model of electro-hydraulic proportional symmetrical valve-controlled asymmetrical hydraulic cylinder［J］. Machine Tool & Hydraulics， 2020， 48（20）： 54-59， 70.

［17］ 何常玉， 施光林， 郭秦阳， 等. 阀控非对称液压缸位置控制系统自适应鲁棒控制策略［J］. 上海交通大学学报， 2019， 53（2）： 209-216.

He Changyu， Shi Guanglin， Guo Qinyang， et al. Adaptive robust control strategy of valve controlled asymmetric cylinder position control system ［J］. Journal of Shanghai Jiao Tong University， 2019， 53（2）： 209-216.

［18］ 郭庆贺， 赵丁选， 赵小龙， 等. 基于内模控制的主动悬挂电液伺服作动器位置控制研究［J］. 农业机械学报， 2020， 51（12）： 394-404.

Guo Qinghe， Zhao Dingxuan， Zhao Xiaolong， et al. Internal model control in position control of active suspension electro-hydraulic servo actuator［J］. Transactions of Chinese Society for Agricultural Machinery， 2020， 51（12）： 394-404.

［19］ 程帅， 龚国芳， 冯斌. 液压油体积弹性模量综合实验系统设计与分析［J］. 机床与液压， 2011， 39（3）： 1-4.

Cheng Shuai， Gong Guofang， Feng Bin. Research on theoretical model for effective bulk modulus of air-liquid mixtures of hydraulic oil［J］. Machine Tool & Hydraulics， 2011， 39（3）： 1-4.