基于无人机多光谱遥感估算西北半湿润区葡萄基础作物系数研究

徐 灿,胡笑涛,陈滇豫,甄晶博,王文娥,彭雪莲,汝 晨

(西北农林科技大学旱区农业水土工程教育部重点实验室,陕西 杨凌 712100)

作物蒸散量主要包括土壤蒸发和植被蒸腾两部分,是作物与外界进行水分交换的重要途径[1]。作为全球水循环和地表能量平衡的重要组成部分,蒸散量对作物生长发育和产量形成具有重要影响,是确定合理灌溉制度的依据[2]。我国是世界最大的鲜食葡萄生产国和消费国,葡萄种植面积稳定在66万 hm2以上[3],且经济价值可观。作为我国鲜食葡萄重要产区之一,陕西省近年来葡萄栽培面积和产量均有大幅提升[4]。适当的水分供应是保证葡萄高质高产的基本条件之一,葡萄园水分亏缺或过多不仅影响当季葡萄的产量与品质,还会影响下季葡萄生长发育,甚至会缩短葡萄树生长年限,这些均増加了葡萄园水分管理的复杂性和特殊性[5]。确定合理的灌溉制度以满足葡萄生产的必要水分需求具有重要意义,因此准确估算葡萄生育期内蒸散量尤为关键。

常用的获取作物蒸散量的途径分为测定法、直接估算法和间接估算法3类。测定法主要包括涡度相关法、波文比法、蒸渗仪法、同位素法等,国内外很多学者[6-9]已经验证了利用以上方法获取作物实际蒸散量的适用性与准确性;但此类方法大多技术复杂、造价高、维护费用高,且个别方法要求有足够大及平坦均一的下垫面,否则很难达到一定精度。直接估算法主要包括单源模型及多源模型。单源模型中P-M模型具有较强的理论基础,但其忽略了冠层和土壤间的水热特性差异,对稀疏植被的蒸散估算偏差较大;多源模型机理复杂、计算成本高,容易出现“过度拟合”的情况,且参数获取难度大,在实际应用中会受到一定限制。间接估算法中最常用的为作物系数法,其中FAO-56推荐的双作物系数法估算方法简单,得到了广泛应用[10-12],但其有一定的适用范围,并非对所有地区、所有作物的蒸散量都能够进行精准估算。

双作物系数法中的作物系数必须根据作物自身生长状况及外部环境(水分胁迫、气象条件)进行校正才能准确估算实际蒸散量,但随时进行地面监测并对作物系数曲线做出调整存在较大困难,因此利用遥感技术估算作物系数更为可行。Shao等[13]将无人机多光谱遥感技术与随机森林算法结合,获得了不同灌溉条件下玉米作物系数(Kc)的高分辨率空间分布图。Gautam等[14]利用无人机搭载多光谱传感器提取赤霞珠葡萄的光谱和结构特征,通过多元线性回归和机器学习方法对Kc进行建模,结果表明将冠层结构特征和光谱特征相结合,可以提高模型适用性;在所有预测模型中,随机森林预测的Kc精度最高。近年来,遥感技术在国内快速兴起,逐渐应用于不同研究领域并处于较高的发展水平,其在估算作物系数方面的应用有效克服了现有其他研究方法的许多缺陷[15]。遥感应用主要分为卫星遥感和低空机载遥感,卫星遥感发展最早并且已经相当成熟,但其数据的预处理结果易受大气影响而且经常与试验时间不相符,获取较为可靠的数据难度较大。低空无人机遥感不仅克服了卫星遥感受大气状况影响大、重访周期长、时空分辨率不匹配等问题,还规避了地面监测作物生长信息耗时、费力等缺点,具有成本低、机动灵活、能实时采集图像、高时效性、高时空分辨率等一系列优点[16]。无人机遥感技术可以较好地估算日作物系数,从而满足农田尺度估算作物日蒸散量的需求[17]。De Jesús Marcial-Pablo等[18]证明了基于无人机光谱遥感剔除地物背景后的图像可以较高精度地估算玉米Kc,其中Kc与NDVI在80 000株·hm-2时拟合效果最好。张瑜[19]利用无人机多光谱遥感技术协同地面监测建立了作物系数Kc与植被指数的关系模型,并论证了其可行性。韩文霆等[20]利用无人机多光谱遥感技术获取6种植被指数,分别建立了其与大田玉米作物系数在各生育时期不同水分胁迫条件下的关系模型,结果表明在快速生长期充分灌溉条件和生长后期水分胁迫条件下,植被指数SR与作物系数的相关性最好。

迄今为止,我国对作物系数的估算研究主要集中在经济类作物及大田作物,对于根系发达、稀疏种植的多年生果树研究较少;葡萄果树由于株间个体差异大,对水肥管理的要求较高,此类研究更是鲜有报道。不同于密植作物土壤蒸发较小,葡萄果树蒸散中植被蒸腾与土壤蒸发属于两个相对独立的部分,且各自占据较大比重,因此有必要对其基础作物系数Kcb进行单独研究。目前基于无人机遥感技术估算农田尺度稀疏植被基础作物系数的研究明显不足。针对以上问题,本文以2021年西北半湿润区葡萄园为研究区域,以波文比系统实测蒸散量ETc为准,基于彭曼公式法计算参考作物蒸散量ETo,得到葡萄作物系数Kc后,采用FAO-56双作物系数法计算土壤蒸发系数Ke与水分胁迫系数Ks,获得基础作物系数Kcb,利用无人机多光谱遥感影像获取葡萄光谱数据,提取多个波段反射率计算4种植被指数,建立葡萄基础作物系数Kcb与植被指数的关系模型,从而估算葡萄园实际蒸散量,验证无人机多光谱遥感反演葡萄Kcb的精度,以期提高葡萄园蒸散量的估算精度,为该地区精准灌溉提供理论指导及技术支撑。

1 材料与方法

1.1 研究区概况及葡萄物候期

试验于2021年4—8月在陕西省咸阳市杨陵区崔西沟村君度唯尔葡萄庄园进行,该地区位于陕西关中平原中部(108°08′E,34°31′N,海拔524.7 m),属于暖温带半湿润气候区,四季分明,冬季寒冷干燥,夏季高温多雨,多年平均气温12.9℃,年日照时数2 163.8 h,无霜期210 d,多年平均降水量580 mm且主要集中在7、8月份,年平均蒸发量1 500 mm。试验区葡萄龄期大约5 a,品种为‘黑色甜菜’。葡萄的种植行由南向北,行距约为3 m,每行葡萄藤之间的间距为0.8 m左右,葡萄架式为单篱架,架高1.5 m左右,沿葡萄种植方向每隔3～4 m设立水泥柱,并在上中下拉3道钢丝。葡萄园灌溉方式以滴灌为主,灌水、施肥等田间管理措施均与当地葡萄生产一致,不进行特殊水肥调控。根据葡萄生长特性,将其全生育期划分为4个生育阶段,分别为新梢生长期(4月12日—5月15日),开花期(5月16日—5月30日),果实膨大期(5月31日—7月6日),着色成熟期(7月7日—8月18日)。

1.2 多光谱影像采集与预处理

研究采用深圳市大疆创新科技有限公司的四旋翼精灵Phantom 4无人机为数据采集平台,该无人机为一体式的多光谱成像系统,多光谱相机有6个影像传感器,其中1个彩色传感器用于可见光(RGB)成像,5个单色传感器用于包含蓝(B, 450 nm±16 nm)、绿(G, 560 nm±16 nm)、红(R, 650 nm±16 nm)、红边(RE, 730 nm±16 nm)和近红外(NIR, 840 nm±26 nm)波段的多光谱成像。试验设置无人机航线条,相对航高30 m,航向重叠率80%,旁向重叠率70%,地面分辨率为1.6 cm,作业过程中可同步获取研究区RGB和多光谱影像。无人机多光谱遥感影像数据采集选择晴朗无风无云、太阳光照稳定的天气进行,整个生育期共获得60组数据。获取的多光谱影像检查无误后导入DJITerra软件中,选择农田场景进行二维重建,得到基于单个波段的正射影像。将拼接完成的单个波段影像导入ENVI 5.3软件中,进行波段合并,最后得到多个波段融合后的葡萄园多光谱影像。利用Matlab对多光谱影像进行背景剔除后,提取不同波段反射率计算多种植被指数。

1.3 气象数据

试验区净辐射、风速、风向、空气温度、相对湿度、水汽压、土壤热通量等气象数据由波文比系统全天候每10 min自动观测记录。降雨量由杨陵气象站提供,参考作物蒸散发量利用彭曼公式(式1)计算,具体见图1。

(1)

式中,ETo为参考作物蒸发蒸腾量(mm·d-1);Rn为作物冠层的净辐射(MJ·m-1·d-1);G为土壤热通量(MJ·m-1·d-1),在逐日计算中G=0;T为平均气温(℃);u2为2 m高处的平均风速(m·s-1);es为饱和水汽压(kPa);ea为为实际水汽压(kPa);Δ为饱和水压与温度曲线的斜率(kPa·℃-1);γ为干湿表常数。

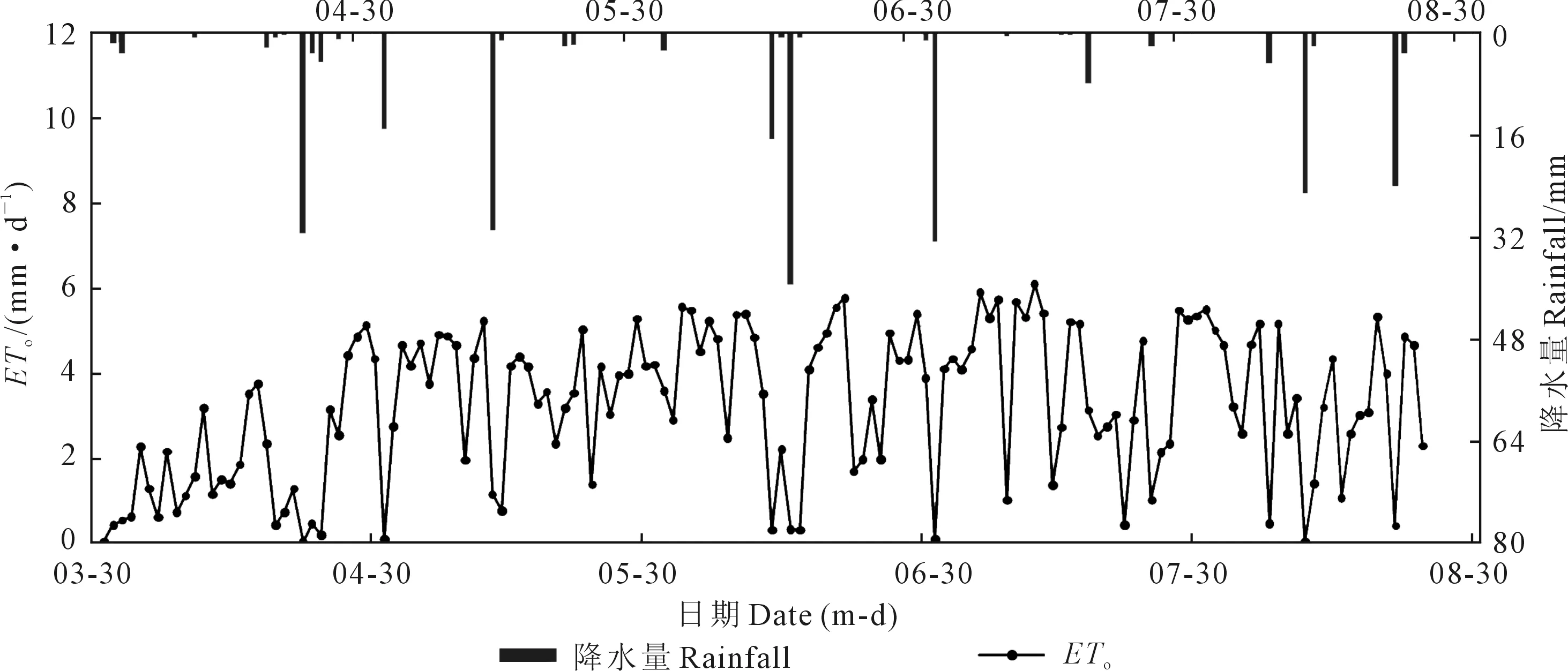
图1 参考作物蒸散发量及降雨数据

1.4 波文比能量平衡法

波文比能量平衡法是应用广泛的估算农田蒸发蒸腾方法,该方法通过测量温度和湿度梯度,结合净辐射以及地面热通量的测定来估算潜热通量[21]。其基本原理是能量守恒,优点是所需实测参数少,计算方法简单,不需要有关蒸发蒸腾面空气动力学特性方面的资料,并可以估算大面积(约1 000 m2)和小时间尺度(10 min)的潜热通量。能量平衡方程基于能量守恒原理,表示下垫面所有吸收与释放能量的总和,其计算方法如式(2)所示:

Rn=λET+H+G+AD+PH+M

(2)

式中,Rn为净辐射(W·m-2);λET为潜热通量(W·m-2);λ为汽化潜热(J·kg-1);ET为蒸发蒸腾量(mm);H为显热通量(W·m-2);G为土壤热通量(W·m-2);AD为能量水平交换量(W·m-2);PH为光合作用能量转换(W·m-2);M为植物代谢引起的能量转换以及植物内部与冠层空间的热量储存(W·m-2)。

如果下垫面均一且面积较大时,各气象因素的铅直梯度远大于水平梯度,因此,平流作用产生的能量水平交换量AD可忽略不计。而PH和M之和通常比测量主成分时产生的实际误差还小,一般情况下也可忽略,故式(2)可简化为:

Rn=λET+H+G

(3)

1.5 双作物系数法

双作物系数法仅需要常规气象要素,因其方法简单而被广泛应用于计算1 d或更长时段的蒸散量[22],其计算公式如下:

(4)

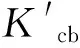
Ks为土壤水分胁迫系数,采用FAO-56推荐的计算公式如下:

(5)

TAW=10γZr(θfc-θwp)

(6)

Dr=10γZr(θfc-θ)

(7)

RAW=pTAW

(8)

式中,TAW为作物主要根系层总的土壤有效储水量(mm);RAW为易被作物根系利用的根区土壤储水量(mm);Dr为计算时段作物根区土壤水分的平均亏缺量(mm),当计算时段较短时,可用时段初的土壤水分亏缺量来代替;γ为土壤体积密度(g·cm-3);Zr为作物根系主要活动层深度(cm);θ为时段初作物根系层平均土壤含水率(m3·m-3);θfc和θwp分别为根区田间持水量(m3·m-3)和根区凋萎含水量(m3·m-3);p为根区中易被作物根吸收的土壤储水量与总的有效土壤储水量的比值,一般介于0～1.0。

Ke为表层土壤蒸发系数,本文采用FAO-56推荐的计算公式如下:

Ke=Kr(Kcmax-Kcb)≤fewKcmax

(9)

式中,Kcmax为降雨或灌溉后作物系数的最大值;Kr为由累积蒸发水深决定的土壤蒸发衰减系数,当土壤表面较为湿润(降雨1～2 d)时,Kr取值为1;降雨后3～5 d,地表湿润度降低,Kr取值为 0.7;降雨后6～8 d,地表水分持续减少,Kr取值为 0.2;当地表用以蒸发的水分完全耗尽时,Kr取值为 0;few为发生棵间蒸发的土壤占全部土壤的比例。

Kcb为基础作物系数,计算公式如下:

(10)

式中,ET为实际作物蒸发蒸腾量(mm),本文实测值由波文比系统提供;Ks和Ke分别利用公式(5)、(9)求出。

1.6 植被指数计算

本文初步选用4种常用的植被指数进行计算(表1),其中NDVI可以检测植被生长状态、植被覆盖度和消除部分辐射误差;SAVI增加了土壤调节系数,可降低NDVI对土壤背景的敏感;RVI是绿色植被的灵敏指示参数,对高覆盖植被区域更为敏感,与生物量的相关性最好;DVI对土壤背景的变化极为敏感。

1.7 模型检验方法

选择均方根误差(RMSE)和模型性能指数(EF)[27]评价模型模拟值与实测值之间的验证效果。本文随机选取样区50%的样本数据(30组)作为建模集,基于线性回归方法构建Kcb的估算模型;利用剩余50%的样本数据(30组)作为验证集,评价Kcb估算模型。

(11)

(12)

式中,RMSE为均方根误差(mm);EF为模型性能指数;Pi为预测值;Oi为真实值;O为真实值的平均值;n为数据样本数量。RMSE越小,表明模型偏差越小;EF越接近1,表明吻合度越高。

2 结果与分析

2.1 葡萄作物系数与植被指数

葡萄全生育期基础作物系数Kcb、土壤蒸发系数Ke、水分胁迫系数Ks和作物系数Kc的逐日变化曲线如图2所示。由图2可以看出,Kcb随着生育期呈现先上升后下降趋势,生育初期、中期、后期分别约为0.13、0.76、0.33。FAO-56中3个生育时期不同阶段的推荐值分别为0.15、0.80和0.40。与推荐值相比,实际值偏低,这可能是地区气候、品种及耕作措施不同造成的差异[28-29]。

表1 植被指数计算公式

Ke在生育期初期基本维持在一个较高值;随着葡萄的生长发育,冠层覆盖度逐渐增加,导致Ke逐渐减小;而生育后期由于葡萄保产必要的修枝及叶片逐渐老化凋零,土壤蒸发也逐渐增大。此外生育初期Ke波动较大的原因可能是降雨导致土壤含水率发生了变化。Kc为Kcb与Ke之和,生育前期和后期的Kcb值较小,所以Kc变化趋势同Ke几乎一致,而生育中期Kcb对Kc值的影响则较大。Kc在生育初期逐渐增大,生育中期保持相对稳定的较大值,生育后期逐渐减小,此变化规律与FAO-56中的描述基本相符。葡萄整个生育期未产生水分胁迫,故其水分胁迫系数Ks=1保持不变。

葡萄生育期内,4种植被指数(NDVI、SAVI、RVI和DVI)随生育天数的变化如图3所示。由图3可知,4种植被指数均随生育期推进先缓慢增大,而后逐渐呈降低趋势,符合葡萄生长规律。生育前期到生育中期,葡萄冠层覆盖度增加,作物蒸腾作用加强,消耗更多的土壤水分,而土壤蒸发减小,植被指数均增大;生育中期到生育后期,随着葡萄叶片逐渐枯萎,冠层覆盖度降低,土壤蒸发量增加,植被指数均降低。其中,生育中后期开始,RVI有较大的下降趋势,这是因为RVI对作物的覆盖度变化比较敏感,适用于监测高覆盖度植物冠层的动态变化[30]。

图2 葡萄生育期作物系数变化曲线

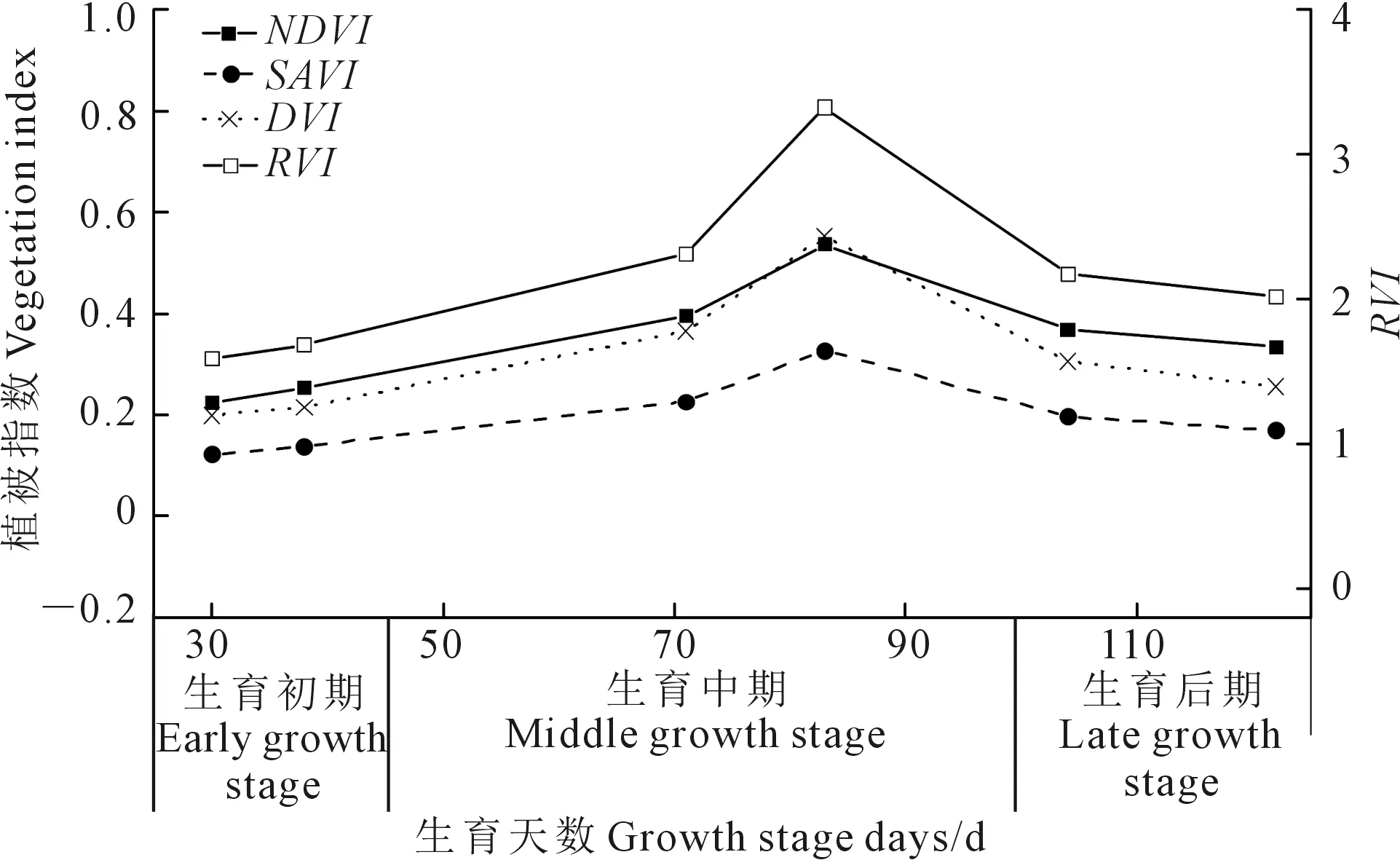
图3 葡萄生育期植被指数变化曲线

2.2 葡萄基础作物系数与植被指数关系模型

本研究选取相关性较高的4种植被指数(NDVI、SAVI、RVI、DVI)来建立植被指数与葡萄基础作物系数之间的一元线性回归模型、多项式回归模型及多元线性回归模型。把葡萄整个生育阶段分为生育前期和生育后期两个阶段,即萌芽开花期(无葡萄果实)为生育前期,果实膨大及着色成熟期为生育后期,对两个时间段分别建立植被指数与葡萄基础作物系数Kcb的关系模型。

生育前期、后期葡萄植被指数与基础作物系数Kcb的关系如表2所示。由表2可知,在生育前期和后期4种植被指数与葡萄基础作物系数Kcb的决定系数较高(R2>0.60),基本上能满足拟合精度要求(P<0.01)。这是因为植被指数能够反映植被的覆盖情况及生长活力,在一定条件下能定量说明植被的生长状况;而基础作物系数用来描述作物蒸腾,不考虑土壤蒸发,与作物的生长情况相关,所以两者有较强的相关性。其中生育前期和后期Kcb与NDVI决定系数分别为0.82和0.71、与SAVI决定系数分别为0.75和0.74、与RVI决定系数分别为0.80和0.75、与DVI决定系数分别为0.65和0.75。对比得知,NDVI和RVI与不同生育阶段的Kcb均有较高而且稳定的相关性。这可能是因为NDVI和RVI能充分反映植被在近红外波段和红光波段反射率的差异,还可增强植被与土壤背景之间的辐射差异,是植被长势和丰度估算的主要手段;两种波段可能对冠层蒸腾有较强的敏感性,因此在葡萄不同生育阶段都可以很好反映作物蒸腾能力[31]。

与单项式模型相比,采用多项式回归建立的植被指数与葡萄基础作物系数Kcb的模型拟合精度都有所提高,但效果不显著,这可能是因为单项式植被指数反演葡萄作物系数模型本身就具有较高拟合精度,但单一变量考虑因素有限,无法全面表征不同因素对作物系数的影响程度。

全生育阶段4种植被指数与葡萄基础作物系数Kcb的一元线性回归模型及多项式回归模型如图4所示。由图4a～d可以看出,4种植被指数拟合Kcb效果较好(R2>0.65),说明用植被指数拟合葡萄作物系数具有一定可行性。Kcb在生育前期逐渐增加,生育中期达到最大值,生育后期逐渐降低;植被指数的变化规律与其基本一致。由于Kcb在葡萄生育过程中存在先上升后下降两个阶段,因此可能出现相同Kcb值对应多个植被指数值的现象。这种现象较易出现在生育中期,即Kcb值较大时。

由图4e～h可知,与生育前期、后期变化规律一致,全生育阶段葡萄4种植被指数与基础作物系数Kcb的多项式回归模型精度也均比一元线性回归模型精度有所提高。而全生育阶段Kcb模型精度较生育前期及生育后期有所降低,这是因为不同生育阶段植物生长情况不同,用同一关系式进行拟合,便会出现精度不高的问题。图4数据主要集中在3部分,主要是因为FAO-56列出了葡萄生育初期、生育中期、生育后期的基础作物系数典型值,而基础作物系数在生育过程的变化通过线性插值获得。本研究的Kcb值仅在FAO-56基础上对气象影响进行了修正,与典型值的差距不大,未经线性插值,所以存在分布不均衡的情况。

表2 生育前期和后期葡萄植被指数与基础作物系数Kcb的关系

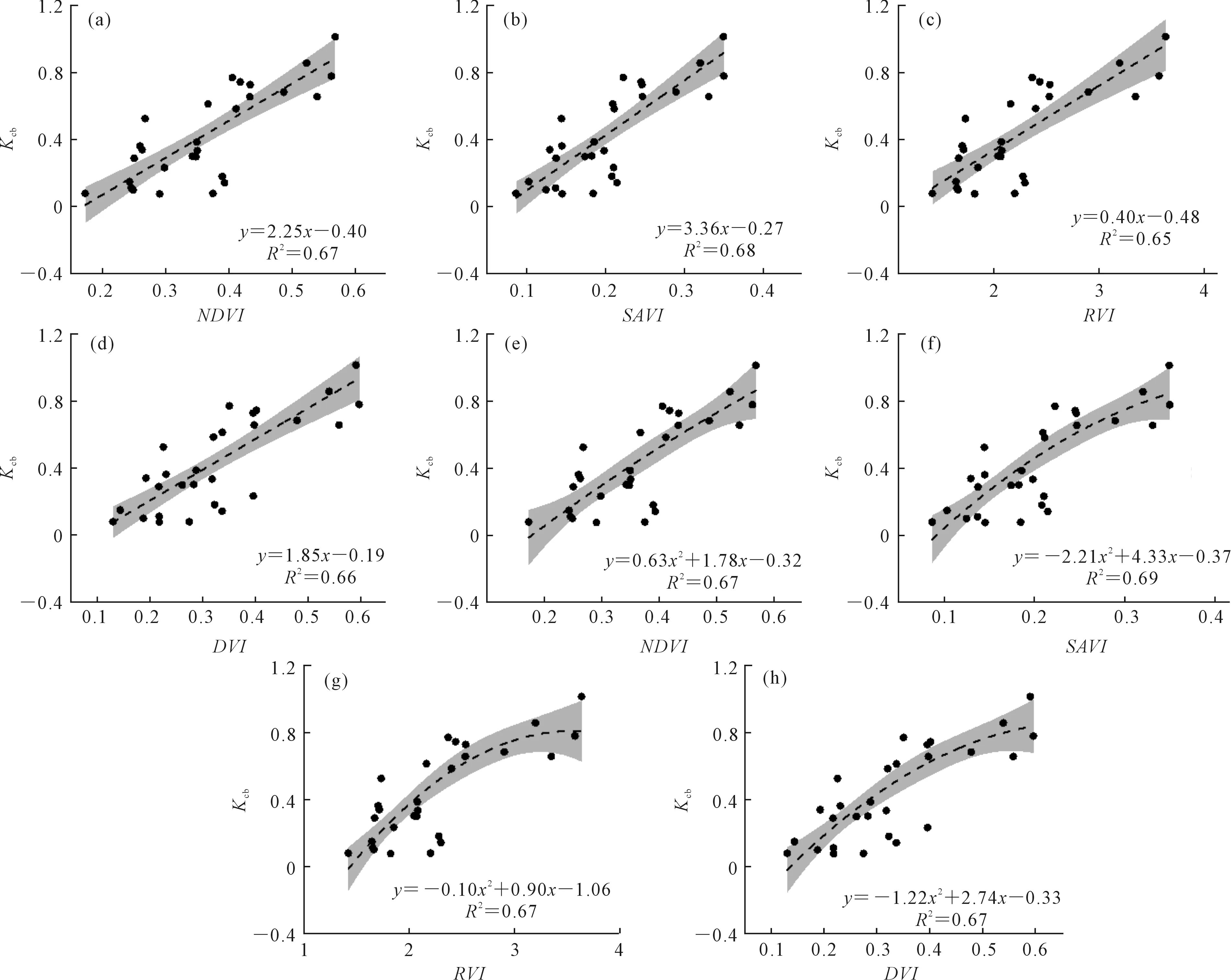
注:图a～d为一元线性回归模型拟合结果,图e～h为多项式回归模型拟合结果。

生育前期、生育后期及全生育阶段4种葡萄植被指数与基础作物系数Kcb的多元线性回归模型如表3所示。由表3可知,生育前期及生育后期Kcb-VIs多元线性回归模型精度分别为0.86和0.78,全生育期阶段Kcb-VIs精度较好(R2=0.71)。生育前期、后期及全生育阶段Kcb-VIs多元线性回归模型精度均高于一元线性回归模型及多项式回归模型,这主要是因为多元线性回归模型不再只考虑单一植被指数对Kcb的影响,而是引入了多种植被指数综合考虑,提高了自变量与多个因变量的相关性[30]。

2.3 蒸散量估算精度验证

生育期内利用波文比系统自动监测的葡萄实际日蒸散量及其与FAO-56双作物系数法估算的蒸散量对比如图5所示。由图5a可知,整个生育期内,葡萄实际蒸散量呈现先增大后减小的变化趋势,生育前期和后期波动较小,生育中期变幅增大,其波峰出现在降水偏少、阳光充足、气温较高的6月份,此时葡萄生长最为茂盛,处于果实膨大期,波谷则出现在降雨最为集中的7月份。葡萄实际蒸散量的变化范围为0.10～6.39 mm·d-1,根据波文比法计算出的全生育期葡萄实际蒸散量为319.88 mm。由图5b可知,将FAO-56推荐的双作物系数法估算得到的葡萄实际蒸散量与波文比系统实测值进行对比,精度较好(n=118,EF=0.58)。双作物系数法估算值普遍偏高,这是因为作物系数受气候条件、土壤、作物栽培管理方式和作物生长状况等诸多因素影响,其估算精度不尽相同,存在一定的局限性[32]。

表3 不同生育时期4 种葡萄植被指数与基础作物系数Kcb的多元线性回归模型

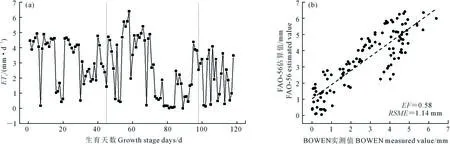
图5 生育期内波文比葡萄实际蒸散量及FAO-56 双作物系数法估算值与波文比实测值对比

利用表2得到不同植被指数与Kcb的一元线性表达式后计算不同生育期葡萄实际蒸散量,结果如图6所示。不同生育阶段利用植被指数与Kcb一元线性建模估算葡萄实际蒸散量效果均较好,验证精度大多在0.65以上,效果均优于FAO-56双作物系数法(EF=0.58,RMSE=1.14 mm)。

在生育初期,SAVI和DVI散点基本上对称分布且集中在1∶1线附近,验证效果较好(EF>0.75);而NDVI和RVI散点基本上也对称分布且集中在1∶1线附近(图6a～d)。在生育后期,4种植被指数验证效果较为稳定(EF=0.64～0.73),实测值均略高于预测值,并且当同一生育阶段蒸散量增大时,反演效果有所下降(图6e～h)。在全生育阶段,4种植被指数验证蒸散量的差异不大,RMSE基本上在0.13 mm左右(图6i～l)。综合3个生育阶段结果可知,基于植被指数通过一元线性回归模型反演葡萄基础作物系数,从而估算不同生育时期葡萄蒸散量,各植被指数表现为:DVI>SAVI>RAVI>NDVI。

利用表2建立不同植被指数与Kcb的多项回归关系式,计算得到生育前期、后期及全生育阶段葡萄实际蒸散量估算值如图7所示。多项式回归模型与一元线性回归模型相比,两者验证效果差别不大。在生育后期,多项式回归模型下4种植被指数的验证精度基本都有小幅提高,而生育前期和全生育阶段选取一元线性回归模型验证精度最好,说明采用多项式并不能完全提高验证效果。可能是因为单项式本身已经达到很高的验证精度,且采用多项式无法解决同一生育阶段蒸散量增大时验证精度下降的问题,甚至还有进一步增大误差的趋势。

利用表3多元线性回归建模后,计算得到的生育前期、后期及全生育阶段葡萄实际蒸散量估算值如表4所示。生育前期(EF=0.75)、后期验证精度(EF=0.80)高于全生育阶段验证精度(EF=0.73),这可能是由于生育期内无人机飞行次数有限,且葡萄不同生育阶段生长规律变化较大,很难获取可以代表全生育阶段的拟合关系式。与一元线性回归和多项式回归模型相比,各生育阶段多元线性回归模型的验证精度并未显著提高,这可能是因为多元线性回归模型引入了多种植被指数特征参数,模型复杂度较高[30],无法很好地拟合非线性数据;同时本研究选取的4种植被指数可能适用性不强或它们之间共线性较强[33],对模拟造成了一定影响。

3 结 论

1)一元线性回归和多项式回归建模条件下,在葡萄生育前期,NDVI、RVI与Kcb模型拟合精度优于DVI、SAVI,拟合效果最佳;在生育后期及全生育阶段,4种植被指数与Kcb模型拟合精度之间差异不大。多元线性回归建模条件下,生育前期拟合效果最好(R2=0.86),其次是生育后期(R2=0.78)和全生育阶段(R2=0.71)。

注:图a～d为葡萄生育初期验证结果,图e～h为生育后期验证结果,图i～l为全生育阶段验证结果。下同。

2)不同反演模型对葡萄实际蒸散量的估算精度不同。在生育前期,利用DVI与Kcb建立的多项式回归模型的验证精度最高(EF=0.79);在生育后期,多元线回归模型验证精度最高(EF=0.80);在全生育阶段,利用DVI与Kcb建立的一元线性回归模型的验证精度最高(EF=0.73)。

图7 生育前期、后期及全生育阶段多项式回归模型估算精度验证

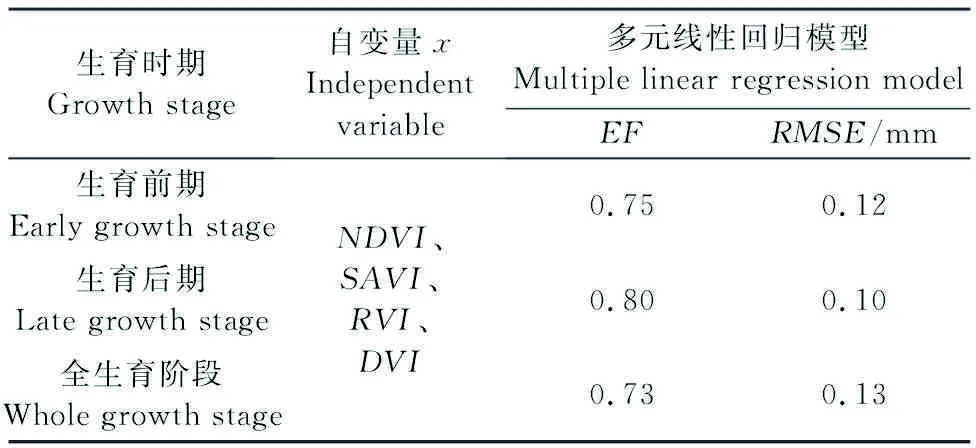
表4 生育前期、后期及全生育阶段多元线性回归模型估算精度验证

3)根据葡萄生长特性,分生育阶段选择合适的植被指数及建模方法反演Kcb值可较FAO-56双作物系数法的Kcb推荐值对蒸散量的估算精度提高6%以上。