基于OMS算法的LDPC译码算法改进∗

吴少峰 杨春兰 黎德文

（中国船舶集团有限公司第七二二研究所 武汉 430205）

1 引言

LDPC 码是Gallager 于1962 年首先提出的［1］，Mackay 等人发现LDPC 码在较低复杂度的情况下具有逼近容量限的性能，相较于Turbo 码，LDPC 码误码性能更好、错误平层更低、构造灵活、译码吞吐更高［2］，在无线通信系统中受到了广泛的关注，如WiMAX、数字视频广播（DVB）、IEEE802.11［3］和ATSC［4］。特别是在增强移动宽带（eMBB）场景中，3GPP选择了它们作为第五代移动通信（5G）中数据传输的纠错码［5］。

如今主流的LDPC 编码算法主要包括两种，分别是根据生成矩阵G和根据具有特殊结构的校验矩阵H 进行编码。本文主要介绍其中的准循环码编码方法。准循环码（QC-LDPC）具有存储复杂度和编码复杂度低的特点，因此3GPP决定在5G中使用两种QC-LDPC 基矩阵，分别命名为BG1 和BG2，它们都支持速率兼容和数据扩展传输。5G 中使用基图的具体结构如图一所示。在本文中，我们以基图BG1为基础进行研究，因为BG1针对更大的块长度和更高的速率，基图BG1 有46 行，68 列，22 个信息位列。

LDPC码译码方面，LDPC译码算法其根本的思想是变量节点和校验节点进行不断的迭代更新，每一次迭代更新过程就是变量节点和校验节点之间信息交换的过程。当前误码性能最好的译码算法是基于后验概率的BP 译码算法，但其计算复杂度高，实际情况难以应用。1998 年，Fossorier 等［6］提出最小和（MS）算法，通过比较出的最小值来更新校验节点消息，有效降低了计算复杂度，同时也来带了一定损失。为了进一步提高译码性能，许多学者又提出了一些改进算法：偏移最小和译码算法（OMS）［7～9］和归一化最小和译码算法（NMS）［10～11］，两种译码算法都是从LDPC 码译码的迭代过程进行性能上的改进。

2 OMS算法改进

2.1 OMS算法

在介绍OMS 算法前我们首先对需要用到的变量进行一些注释。

H(m),H(n)：相邻的变量、校验节点

βm,n,αm,n：校验节点m 和变量节点n 节点之间的信息更新；

β1，β2，β3：BP、MS、OMS 算法中校验节点m到变量节点n 的信息更新；

dc：校验节点的度；

首先是校验节点的迭代过程，在BP算法中：

可以看到BP算法中含有大量的双曲正切函数的运算，运算复杂度非常高，译码过程相对复杂。因此，MS算法用近似值代替双曲正切函数的运算，过程如下：

如果译码器解出了码字或者达到了最大迭代次数后停止工作。在MS 译码算法中，校验节点的近似处理会导致对校验节点消息的过高估计，从而降低译码器的性能。为了克服这个问题，OMS算法和NMS算法应运而生。。

OMS 算法具体操作为在更新每个校验节点时通过减去一个偏移因子β来改进性能：

其中

NMS 算法具体操作为在更新每个校验节点时乘以一个小于1的归一化常数α来提高性能：

从式（3～4）可知，目前不论是NMS 算法还是OMS算法，思路都是通过加入因子参与计算获得更加精确的近似值，但不难发现在这两种算法的迭代过程中加入因子的值是一个不随迭代过程变化的固定值，这理论上会造成一定的近似偏差从而导致算法译码性能的损失。

2.2 改进的OMS算法

本文在OMS 算法的基础上提出一种改进的OMS 算法，提升算法的译码性能，其本质就是要找到与BP 算法中双曲正切函数更为接近的近似值，本文提出的改进之处主要体现在两个方面，其一是加入参数γ作为乘性因子，目的是对每次迭代求偏移因子的范围进行更加精确的控制，γ的取值参照文献［12］设置为固定值；其二是通过密度进化理论求出每次迭代过程中的偏移因子值β，保存在储存单元中，后续直接提取使用［13］。下面给出改进的OMS算法的校验节点更新公式：

由式（2～3，5）可知，β1和β2有着相同的符号，即sgn(β1)=sgn(β2)且β1的数值小于β2，接下来我们先计算初次迭代时所需要的β值。

首先，根据β1和β2分别求出它们的均值E(|β1|)和E(|β2|)，初次迭代时的β值即为两者之差。

其中，P（·）为γn对应的概率密度函数。

我们继续计算第一次以后的迭代需要用到的β值，令式（5）中，可以得出X 的概率分布函数如公式（9）：

因此得出每个量化节点的概率密度函数：

故得出β3的均值：

最后得出后续每次迭代中β值：

3 改进的OMS算法仿真

本节包括对不同译码算法的译码性能仿真比较和不同算法的复杂度分析。在本节中，我们使用5G 标准下的基图BG1 的LDPC 码，码率设置为0.5，码长N=8448，其中信息位长度K=4224，移位因子Z为192，最大迭代次数设置为20次。

3.1 译码性能仿真比较

首先，我们探究偏移因子随着迭代次数变化对改进OMS 算法译码性能的影响。上述仿真条件下，偏移因子β与迭代次数的关系如图1所示。

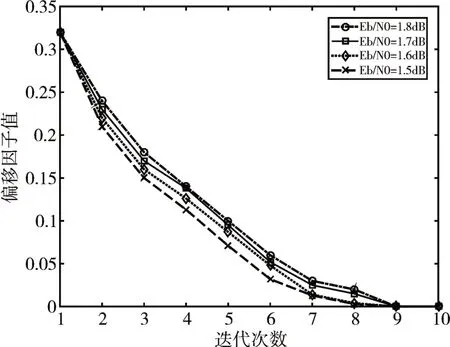
图1 偏移因子β 与迭代次数的关系

从图1 我们可以看到，偏移因子值的大小随着迭代次数的增加逐渐减小，在迭代次数到达第9 次时，偏移因子变为0。如式（8）和式（13），初次偏移因子值是MS 算法和BP 算法信息迭代过程中的均值之差，后续偏移因子值是OMS 算法和BP 算法信息迭代过程中的均值之差，随着迭代过程的进行，两者的差值逐渐变小，证明了迭代过程的正确性；另一方面，如图1 可见，信噪比降低时，偏移因子有着更为明显的下降趋势。

其次，通过仿真得出我们需要的每次迭代过程中的最优偏移因子值后，我们将BP 算法、MS 算法、OMS 算法、NMS 算法以及改进后的OMS 算法的译码性能进行仿真，其中OMS 算法和NMS 算法的参数参照文献［14］和文献［15］设置，归一化因子α=0.7，OMS算法中β=0.4，改进后OMS算法中固定参数γ=0.89，结果如图2。

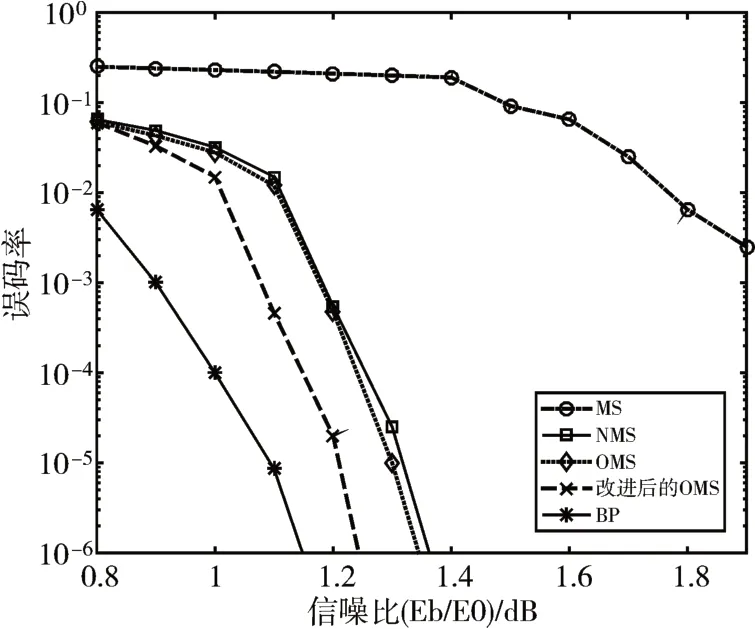
图2 不同算法误码率性能比较

仿真结果表明，在误码率为10-5的情况下，本文提出的改进OMS 算法经过20 次译码迭代，译码性能相较于原OMS 算法提升了约0.13dB，较NMS算法提升了约0.15dB，其性能也更接近与BP算法。

最后，我们对不同译码算法的平均迭代次数进行仿真，结果如图3。平均迭代次数是译码算法收敛能力的反映。从图3 我们可以看到，MS 因其迭代过程中近似性不好，平均迭代次数更多，其算法复杂度更高。改进后的OMS 算法在相同条件下较原OMS 算法收敛速度更快，平均迭代次数更少，在相同迭代次数时也有更好的性能表现。

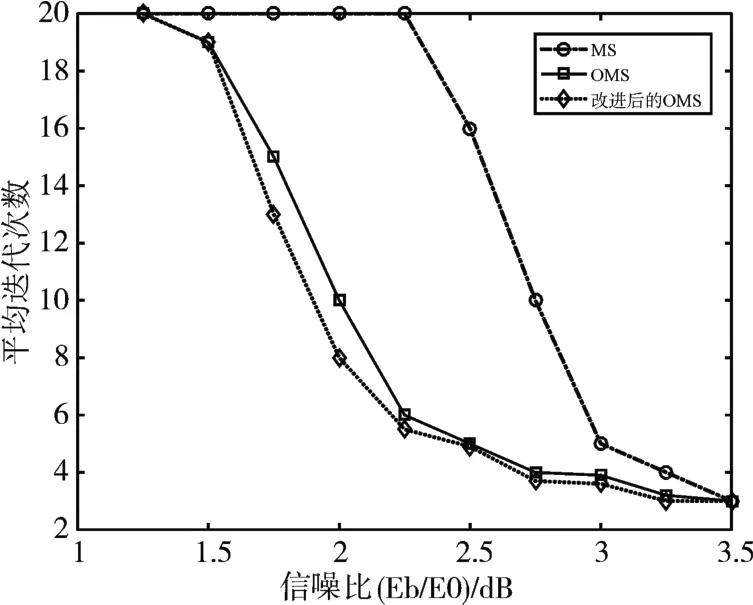
图3 不同译码算法的平均迭代次数对比

3.2 复杂度分析

表1 和表2 分别表示了不同算法在FPGA 实现时译码过程中一次信息更新所需的硬件情况和不同运算的硬件需求情况，其中N 表示在（N，K）的LDPC 码所对应的校验矩阵中非零元素的个数，在FPGA硬件中异或操作和加法的完成方式是完全相同的。

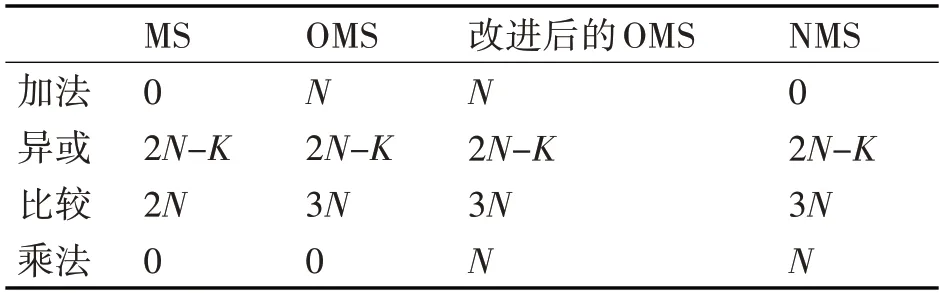
表1 译码过程中信息一次更新所需运算情况

表2 不同运算的硬件需求情况

因此综上仿真结果与数据分析，改进后的OMS算法相较于原OMS 算法，在消耗逻辑元器件提升14.2%和存储位相同的情况下，在误码率为10-5量级有约0.13dB 的误码率性能提升；相较于NMS 算法，所消耗逻辑元器件增加了12.9%，消耗存储位增加了6.2%，但译码性能在误码率为10-5量级时有0.15dB 的提升，在FPGA 实现时，此程度的复杂度提升是可以处理的，不会增加硬件成本。

4 结语

为了提高LDPC 码在5G 移动通信中的纠错性能，本文提出了一种改进的偏移最小和译码算法。在原OMS 算法的校验节点更新环节中，首先加入一个乘性因子γ，其次通过密度进化理论计算出每次迭代的偏移因子，再运用于迭代过程中。仿真结果表明，本文提出的改进OMS 译码算法在相同的复杂度情况下对比现有的OMS 译码算法有约0.13dB 的增益，与NMS 算法相比在复杂度提升不到15%的条件下获得约0.15dB的增益。