基于DoDAF的无人潜航器作战效能静态评估研究∗

隋先辉 韦定江 王晗秋 魏霄冉

（1.海军大连舰艇学院导弹与舰炮系 大连 116018）（2.海军大连舰艇学院学员二大队 大连 116018）（3.清华大学数学科学系 北京 100084）（4.国防科技大学学员五大队 长沙 410073）

1 引言

当前我国周围的形势错综复杂，并随着时代的发展进步，无人化装备已经成为我国周边海域斗争的重要力量。无人潜航器（Unmanned Underwater Vehicle，UVV）作为一种具备良好隐身性能的小型化水中武器逐步登上了斗争的舞台。未来的无人潜航器使用也将立足于联合作战的体系背景，逐步实现集群化的协同作战行动。因此，无人潜航器协同作战效能评估模型的确立将极大地促进未来潜航器的发展。

2 无人潜航器协同作战指标体系构建方法

无人潜航器的协同作战是指多架无人潜航器整合各自作战空间资源及其占位，协同有效的实现作战任务，这将是未来海战场无人作战模式的主要发展趋势之一。在执行作战任务达到作战目的前，作战指挥人员需对作战实施方案进行整体作战效能的评估分析。因此，确立一个合理有效的无人潜航器协同作战指标体系，可有效提高作战效率。

2.1 基于DoDAF的建模过程

DoDAF（Department of Defense Architectural Framework）作为一种描述体系结构、作战活动分析的重要工具和一种顶层框架模型研究体系结构的框架模型及顶层概念，可用于体系结构开发及为决策者制定方案提供支撑，通常适用于构建与分析体系结构。目前，国内李大喜利用DoDAF 视图产品，实现了空基反导装备体系结构可执行模型的构建［1］；高松基于DoDAF 实现了DoDAF 针对于岛礁防空的岛礁防空反导电子对抗装备体系顶层框架概念的构建［2］，王瑛基于DoDAF 和ADC 法得到无人机协同作战效能评估模型［3～4］。综上根据其他的研究经验，可将DoDAF建模过程分为如下几个步骤。

1）作战任务描述：利用DoDAF 将作战使命任务转化为高级作战概念图如图1，使得作战指挥人员可对作战任务有更加直观深入的了解［5］。

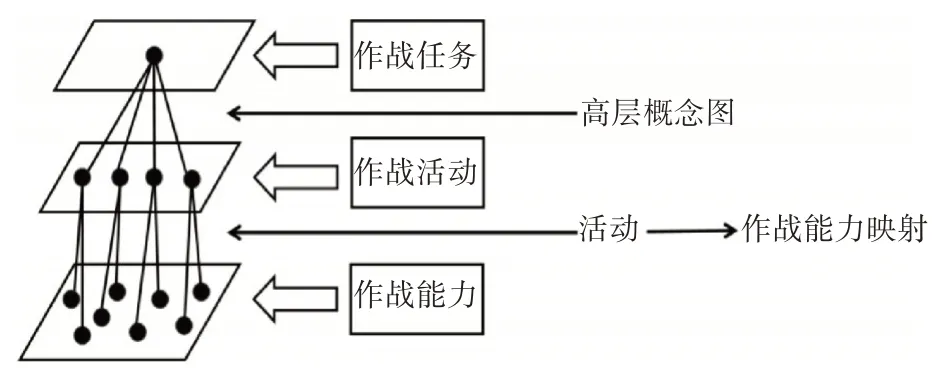
图1 作战任务分解的过程

2）作战活动描述：依据作战使命，将作战的全过程依据时序关系变为若干个作战子任务，并据此梳理分析作战活动间的任务层次关系，最终得到活动分解视图。

3）作战能力描述：建立无人潜航器和联合作战行动间的作战映射关系，并根据关系对能力指标进行分解为子能力和子指标需求，其主要内容包括系统功能追踪矩阵、能力矩阵等。

综上所述，我们可构建任务—行动—能力的逻辑关系图，从作战使命任务分析得到效能评估的体系结构及能力需求。

2.2 无人潜航器作战指标体系的构建

2.2.1 作战想定

现想定敌水面舰艇于某日海域活动，现上级命令我部利用水面舰艇协同无人潜航器进行对海打击。若干个无人潜航器通过水面舰艇运输至相关海域在防区外进行投放，并成功潜行至预定区域展开侦察作业，期间可能受到水下反潜侦察威胁、空中反潜侦察威胁、电子侦察干扰等。无人潜航器探测到敌水面舰艇目标后实施火力打击并判断目标的毁伤状态，进行毁伤评估，而后选择潜行待命或返航。

2.2.2 构建指标体系

1）根据当前局势，对军事需求进行理论分析，分析得到作战使命，并据此构建无人潜航器协同作战高级概念图，刻画作战全过程。

2）对上一步无人潜航器协同作战高级作战概念图中各个作战活动进行分解，生成活动分解视图，如图2。

图2 作战活动概念视图

3）根据活动分析解视图，分析各项活动所涉及的作战能力，得到无人潜航器协同作战活动的能力追踪矩阵如图3，利用能力追踪矩阵，反映出无人潜航器作战活动与其协同作战能力的映射关系如表1。将所需要的能力进一步分析，得到无人潜航器协同作战效能指标体系如图4。

表1 协同作战活动表

图3 作战活动分解图

图4 无人潜航器协同作战指标体系

3 基于ADC 的UUV 协同作战效能评估方法

基本假设：无人潜航器种类相同，出厂时间相同，并记该时刻为0，共有n 台无人潜航器，系统状态Si代表共有i 台无人潜航器故障，作战任务为从时刻t1持续到时刻t2的一个事件，无人潜航器有且仅有两种状态，即故障和非故障，无人潜航器寿命和维修周期相互独立。

3.1 可用性模型

可用性向量A 表示开始执行作战任务时UUV协同编队可能处于的状态，假设UUV 协同作战系统共有n+1个状态（S0，S2，…，Sn），其中n越大代表该系统受损程度越高［6～8］。为了方便讨论，我们不妨假设所有的UUV 都为同一时间出厂，且出厂时刻设为0，则无人潜航器的使用寿命满足指数分布，既在t1时刻前无人潜航器报废的概率为(1-e-λ1t1)。与此同时不妨假设在非作战状态下，因使用寿命而报废的无人潜航器不会进入维修周期。每台无人潜航器的平均故障间隔时间为MT⁃BF 平均修复时间为MTTR，系统延迟时间为MLDT。则每台UUV 在t1时刻能够使用的概率为故可用度为

进而可以得到可用度矩阵(a0,a1,…,an)。

3.2 可信度模型

可信度矩阵D 表示无人潜航器协同作战系统在执行任务中状态改变的概率。假设每种状态之间可以相互转移，dij（t1，t2）代表系统t1时刻处于状态Si而t2时刻处于状态Sj的概率，则D 可表示为如下的n+1阶矩阵：

对单台无人潜航器而言，可假设其为第i台，其在本次任务前的上次检修时间为ti，则该台无人潜航器在执行从t1持续到t2的任务中从能使用状态转变为不能使用状态的概率为

进而可以利用条件概率求得

在某些特定情况下，我们可以假设一次作战行动的行动时长小于无人潜航器的维修时间，那么在这次作战行动中此协同作战系统是不可修复的。且由于单次任务时间远小于无人潜航器报废时间，因此假设在单次任务内无人潜航器不会因为使用寿命而报废，与此同时，我们不妨假设作战开始时所有未故障的无人潜航器都恰好完成检修。在这种情况下，我们只需考虑单次作战的时长T，而可信度矩阵也转变为一个n+1 阶上三角矩阵

引入可靠度R（T）和可用率U（T）来简化计算，其中R(T)=e-λ2T，U(T)=R(T)·Sur，则dij（T）的计算可以简化为

进而可以得到可信度矩阵D。

3.3 能力模型的建立

UUV 作战能力向量为C=[c0c1…cn]T。其中ci表示系统处于状态i时完成任务的概率。为了得到ci的值，需要以下几个步骤：

1）构建指标体系。这个步骤已在2.2.2 中完成。

2）处理指标值。对定性指标，采取直接打分的量化的方法。通过咨询相关专家，并根据已有的经验和知识进行打分，此处采用9个量化级别，如表2所示［9］。

表2 量化级别表

而对于定量指标，则对其进行规范化处理，使其取值范围位于［0，1］区间内。例如，对于效益型指标和成本型指标我们采取极差变换法。

其中xi为指标值。

而对于效益型指标，既效用函数和其取值成线性正相关。

但对于航速而言，由于航速超过30 节后速度继续提升会导致效用函数（自身作战隐蔽性受到影响）下降，故采取如下的规范化处理：

3）指标赋权方法。为了确定不同指标所占比重的差异，需要赋予各个指标对应的权值。采用AHP和Delphi结合的方法，让多位专家确定指标间的相对重要程度dij，由于此处的相对重要程度以比值的方式呈现，故取其几何平均值进而得到判断矩阵C=(cij)n×n，进而求出矩阵C的最大特征值λmax对应的特征向量Y 并进行一致性检验，，RI取值见表3［10］。

表3 RI取值表

当CR ≤0.1时一致性可以接受，否则就重新构造直到一致性得到满足为止［11～13］。

综合上述步骤我们便可以得到能力矩阵C。

4 实例分析

假设某次任务共出动3 架无人潜航器，作战持续时间为1h，UUV 的性能指标如表4，下面计算性能。

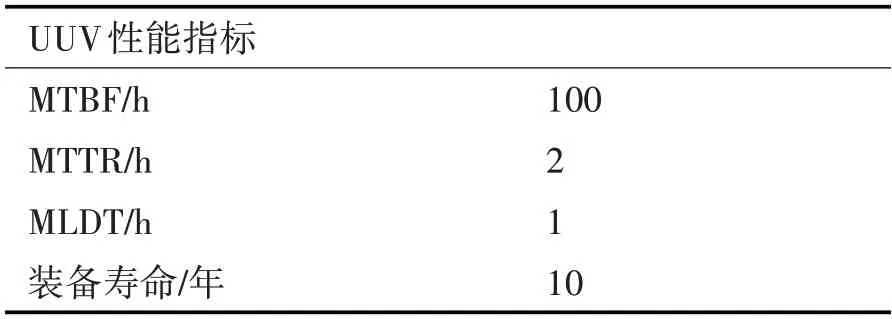
表4 UUV性能表

4.1 可用性向量A计算

执行任务的三架无人潜航器属于并联关系，故该系统共有4 种状态，分别是3 台UUV 全部正常，记为S0；2 台UUV 正常一台UUV 故障，记为S1；1 台UUV 正常2台UUV 故障，记为S2；3台UUV 均故障，记为S3。假设这次出动的三台UUV 均为同一时间出厂，且本次任务在其出厂1 年时进行。则根据上文公式可得到可用性向量A 的每个指标ai的计算方法如下：

经计算可以得到：

A=［0.677 0.281 0.039 0.002］。

4.2 可信度矩阵D的计算

由于本次任务只派出三台UUV，故系统共有4种状态，故可信度矩阵为4 阶方阵。由于本次作战持续时间小于维修所需要的时间且远小于装备寿命，故本次作战过程中系统不可修复，装备使用寿命对UUV 的影响极小可以忽略。与此同时，假设这三台无人机在执行任务前刚刚结束检修，故障时间清零。故直接使用简化模型进行计算，既dij=CijU(T)j(1-U(T))i-j，进而可得到本次作战任务可信度矩阵D的计算方法为如表5。

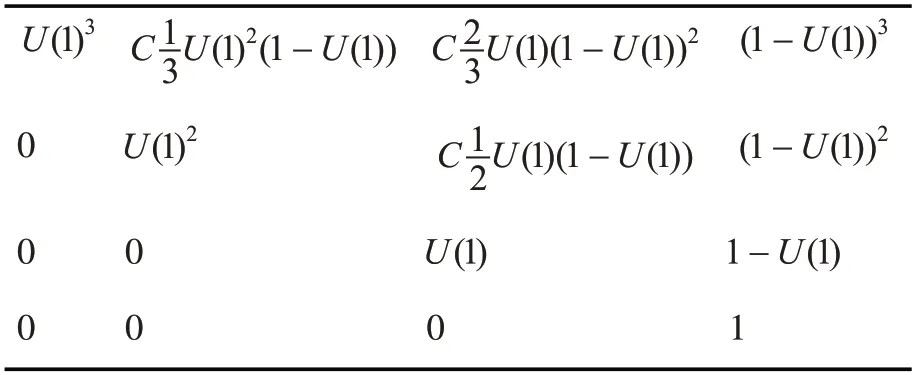
表5 可信度矩阵D计算方法表

矩阵中U（1）代表单台UUV在本次作战过程中的可用率，计算方法如下：

故经过计算可信度矩阵如表6。

表6 可信度矩阵D计算值表

4.3 能力值C的计算

1）定量指标的计算

定量指标主要包括平台系统能力中的平台性能以及作战系统能力中的武器系统。由于本次作战只采用了一种UUV，故在计算过程中省略了对平台性能的讨论。而定量指标大多为线性正相关，故采用归一化与标准化处理，计算得到的计算结果如表7。

表7 武器系统定量指标计算结果表

2）定性指标的计算

定性指标主要包括支援系统能力，信息获取系统能力，指挥系统能力和部分作战系统能力。对于定性指标我们采取专家打分的量化方式得到的结果如表8。

表8 定性指标量化表

3）系统能力向量的计算

采用AHP 和Delphi 结合的方法，得到各项能力指标的权重见表9。

表9 能力指标权重表

4.4 能力值向量的计算

结合前面的计算结果，可以得到本次作战派出3架无人潜航器的能力值为0.794，同理可分别得到派出两架和一架的能力值。进而得到能力值向量如下：

［0.794 0.586 0.326 0］T。

4.5 协同作战效能的计算

结合前面的计算结果，可得本次作战任务的无人潜航器作战效能为：E=ADC=0.653。该计算结果证明该无人潜航器在执行对海目标打击任务时有较好的作战效能。

5 结语

本文结合想定案例分析和计算，在3台UUV协同作战情况下，其中A=［0.677 0.281 0.039 0.002］能力值向量［0.794 0.586 0.326 0］T并得到在该想定案例中，执行本次作战任务的无人潜航器作战效能为E=ADC=0.653。可较好地说明无人潜航器在对海典型作战任务中，完成时敏目标打击任务的效能较好，证明了本文提出的无人潜航器协同作战效能评估方法的有效性。