捷联惯导与计程仪组合导航方法研究∗

张晨阳 蔡 鹏 高大远

（海军潜艇学院 青岛 266000）

1 引言

水下自主航行器（AUV）目前拥有广泛的应用前景，在许多领域都可以看到它的身影，如何实现水下航行器的精确导航一直被诸多学者研究。水下单一的SINS 有自主性强，隐蔽性强等优点，缺点是系统误差会随着时间而增加，长航时情况下会引起导航精度下降。以SINS 为主体，引入其他导航技术，进行组合导航已经逐渐成为一个重要的研究方向。SINS/DVL组合导航系统使用DVL测量的速度参数对SINS 的参数误差进行抑制，可以实现较高的导航精度，所以在水下导航时经常使用SINS/DVL组合导航方法［1］。

针对SINS/DVL 组合导航系统，一般使用扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）［2］等滤波方法。但是，EKF只选取非线性函数泰勒展开式的第一项，忽略了其他高阶项，这样会增加误差，精度有限。而UKF 通过选取少量的采样点来近似描述非线性函数，提高了滤波的精度，但是容易出现协方差矩阵负定的问题，而为了避免滤波算法发散，本文提出采用SRUKF［3］避免该问题，提高了滤波的可靠性。

当模型不够精确或者系统噪声时变时，会导致滤波效果较差，得到的导航参数精度较低。为了提高滤波算法的鲁棒性，本文提出一种交互无迹卡尔曼滤波算法，提高了滤波算法的自适应性。最后，通过仿真实验验证提出算法的有效性。

2 SINS/DVL组合导航数学模型

2.1 状态方程

SINS/DVL 组合导航误差模型［4］分为SINS 误差模型和DVL误差模型。因为SINS垂直通道不稳定并且DVL 的垂直速度测量误差较大，因为仅考虑水平通道问题。

DVL 的测速误差［5］主要包括，速度偏移误差δVd，刻度系数误差δKc，偏流角误差δΔ，因为偏流角误差对测速影响较小，不予考虑。所以，DVL 的误差方程如下：

式中：βd，βK分别表示速度偏移误差和刻度系数误差的相关时间；wd和wK分别是二者的零均值高斯白噪声。

选择SINS的状态变量为经纬度误差（δL,δλ），速度误差（δvx,δvy），陀螺三个轴向的漂移（εx,εy,εz），平台失准角（α,β,γ）。

所以建立状态方程为

2.2 观测方程

SINS/DVL组合导航采用速度组合［6］的方式，把SINS 得到的速度与DVL 测量的速度作差，并把此差值作为观测量输入到滤波器中。

SINS 得到的速度在导航坐标系下的投影为，即：

其中，Vn为速度真实值，为速度误差值。

根据DVL的速度方程可得：

其中，DVL 在载体坐标系下的真实速度为，Vn为导航坐标系下速度的真实值，δKc为刻度系数误差，δVDVL为随机测量误差，为姿态变换矩阵。

所以得到了系统的量测方程，即：

3 SRUKF滤波算法

由于在使用UKF 滤波算法的过程中，有可能出现协方差矩阵负定的情况，这样会导致滤波算法不稳定，得到的状态估计结果也变得发散。SRUKF在UKF［7］的框架下引入了协方差矩阵的平方根形式替代原来的协方差矩阵参与整个运算递推过程，改善了滤波的准确度和可靠性。算法流程［8］此处不再赘述。

4 IMM-SRUKF算法

交互多模型算法（IMM）［9］针对不同的子系统设置不同的滤波器，每个子系统有特定的滤波器，不同滤波器运算时对应着不同子系统状态空间方程。其中，每一个子系统代表的运行轨迹是不同的。

4.1 混合系统模型

假设混合系统一共有z个子系统，J1，J2,…,Jz分别代表子系统1 到子系统z，在初始时刻k=0时，子系统Jn发生概率：

μ1(0)，μ2(0),…,μz(0)满足：

子系统之间的转换概率：

m=1,2,…,z时，pm,n满足：

混合系统由许多个非线性子系统构成，当处于子系统n时，系统一般表达式可描述为

x(k)∊Rnx,u(k)∊Rnu,y(k)∊Rny,分别表示系统的状态，输入，输出；An∊Rnx×nx,Bn∊Rnx×nx,Cn∊Rnx×nx表示适宜维度矩阵；gn:Rnx→Rnx为非线性状态函数；hn:Rnx→Rny为非线性观测函数；w(k),v(k)表示过程噪声和观测噪声，是相互独立的高斯白噪声向量，协方差矩阵分别为Q(k),R(k)。

4.2 IMM算法步骤

IMM的基本原理［10］是，在不同时刻每个滤波器对每个子系统进行状态估计，把不同子系统状态估计结果融合得到最终的状态估计，并在某一时刻把前一时刻的最终状态估计结果作为初始值，带入系统状态方程中，然后针对每个子系统进行滤波。算法最后更新某个子系统的发生概率，计算每个滤波器得到的状态估计结果的权值，进行求和得到最终的系统处于这一时刻的状态估计结果。

具体算法步骤［11～12］如下：

1）混合概率

μm(k-1)表示k-1时刻子系统m发生的概率，pm,n为转移概率矩阵

2）输入交互

(k-1|k-1) 为子系统m的状态估计，Pm(k-1|k-1) 为子系统m的协方差矩阵，(k-1|k-1) 是子系统n的状态估计，P0n,x(k-1|k-1) 是子系统n的协方差矩阵。

3）调用滤波算法

把(k-1|k-1)，P0n,x(k-1|k-1) 作为初始状态，带入到SRUKF滤波算法中。

4）子系统概率更新

似然函数：

子系统概率：

Sn(k|k-1)，(k|k-1)，yn(k)分别是子系统n在k时刻的观测协方差矩阵，观测估计值和观测值。

5）对不同子系统输出结果加权求和

(k|k)，(k|k)分别是子系统n在k时刻的最优状态估计和协方差矩阵，(k|k)和P(k|k)分别是系统在k时刻最优状态估计和协方差矩阵，(k|k)是k时刻系统的观测估计值。

5 仿真实验

将提出的IMM-SRUKF 算法应用到SINS/DVL组合导航系统中，进行仿真验证。设定SINS 系统的

性能参数如下：陀螺仪的常值漂移和随机漂移均设为0.05°/h，加速度计的常值漂移和随机漂移均设为50μg，初始失准角：纵摇角：1.5°，横摇角1.5°，航向角1.5° ；DVL 系统：速度偏移误差δVd=0.10m/s，刻度系数误差δKc=0.001，速度偏移误差和刻度系数误差的相关时间均为100s。

正常状况下，SINS/DVL 的观测噪声没有发生变化。采用SURKF 和IMM-SRUKF 算法得到速度误差和位置误差曲线如图1 所示，从图中可以看出采用SINS/DVL 组合导航提高了导航精度，抑制了速度误差的增长，但是无法消除位置误差的增长。当系统观测噪声没有变化时，采用两种算法得到误差估计结果接近。

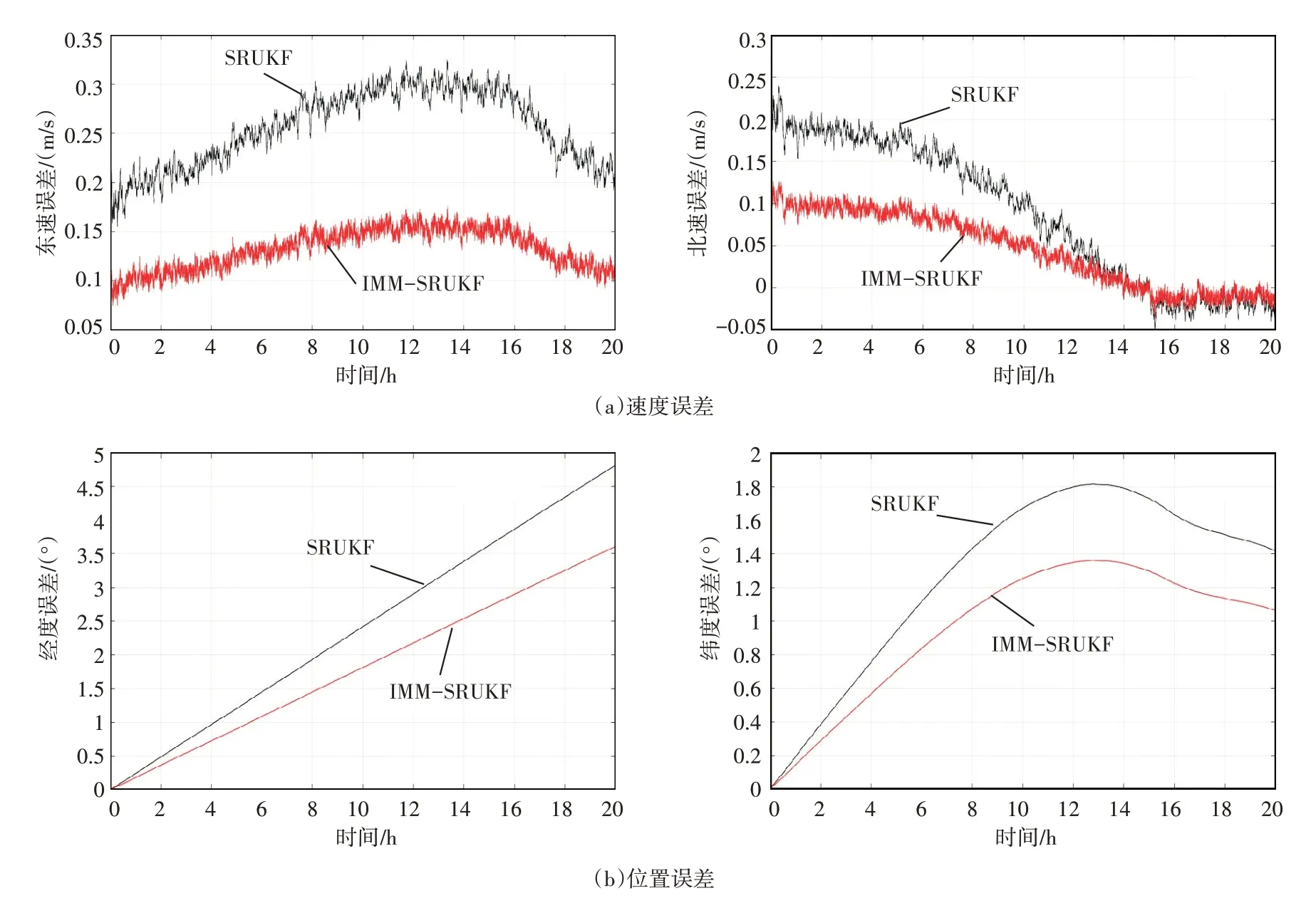
图1 正常情况下的速度误差和位置误差

观测噪声服从高斯白噪声分布，观测噪声协方差矩阵随着时间推移会发生变化，在4h～5h和14h～15h 时将观测噪声增大为原来的4 倍，之后恢复正常。采用两种滤波算法误差估计结果如图2 所示，当观测噪声发生突变时，采用两种算法得到的速度误差和位置误差均发生了突变，导航的精度降低。但是单独利用SRUKF 算法时不能有效地抑制噪声变化带来的误差，并且累积了所产生的误差。而采用本文所提出的IMM-SRUKF 滤波算法时，可以抑制噪声带来的误差，并且产生的误差并不会积累，可以保证导航的精度。

6 结语

本文研究了水下捷联惯导系统（SINS）与多普勒计程仪（DVL）的组合导航问题，根据两种系统的原理和误差模型，建立了SINS/DVL 组合导航模型。在非线性系统滤波过程中，为了避免出现协方差矩阵负定的问题，提出利用SRUKF 算法，提高了滤波算法的稳定性。为了解决观测噪声变化带来的滤波精度下降问题，提出了IMM-SRUKF 滤波算法，提高了算法的鲁棒性。仿真结果证明，提出的滤波算法精度较高，有一定的自适应能力。