破解利器“三板斧”,参数方程最优越
江苏省高邮市第一中学 朱 燕
源于高中数学教材的数学思想方法与技巧策略是课堂教学与学习的关键,合理对比不同的数学思想方法与技巧策略之间的优劣,正确区别并应用优越的技巧方法来破解问题,可以很大程度上减少数学运算,优化解题过程,提升解题效益.
1 源于教材
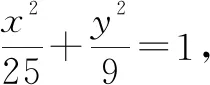
(1)它到直线l的距离最小?最小距离是多少?
(2)它到直线l的距离最大?最大距离是多少?
解决此类涉及椭圆上的点到与椭圆相离的直线(直线与椭圆无公共点)的距离的最小距离与最大距离问题,常用的解法有切线平移法——数形结合、判别式法——代数方程、三角换元法——参数方程等技巧与方法.
2 习题破解
方法1:切线平移法——数形结合.
解析:由直线l的方程与椭圆的方程可知,直线l与椭圆无公共点.设直线m平行于直线l,则直线m的方程可以写成4x-5y+t=0.
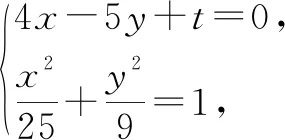
25x2+8tx+t2-225=0.
由判别式Δ=0,得64t2-4×25(t2-225)=0,解得t1=25或t2=-25.
数形结合,由图1可知,当t=25时,直线4x-5y+25=0与椭圆的公共点到直线l的距离最小,且最小距离为
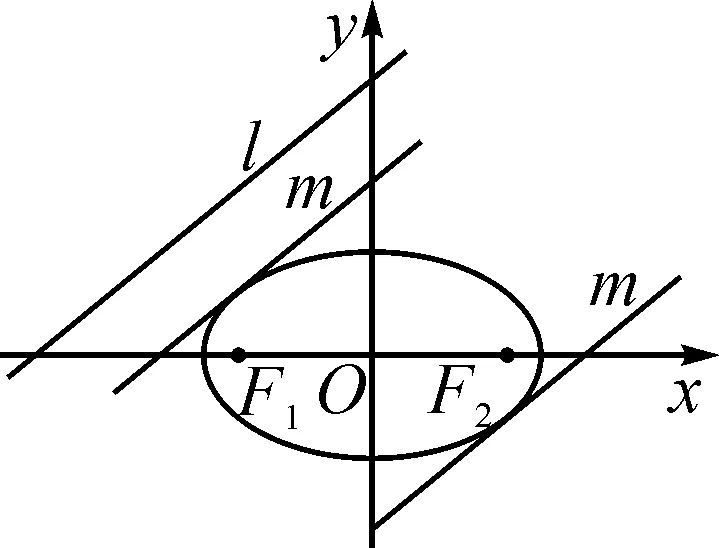
图1
当t=-25时,直线4x-5y-25=0与椭圆的公共点到直线l的距离最大,且最大距离为
解后反思:切线平移法的本质就是利用直线平移确定直线与曲线相切的位置,将椭圆上的点到直线的距离的最小值(或最大值)转化为两平行线间的距离问题来分析与求解.利用两直线平行的性质合理设置平行线方程,并通过直线与椭圆的方程联立,借助判别式为零来确定对应的参数值.数形结合分别求出不同场景下的参数值以及对应的最值关系是破解问题的关键.
方法2:判别式法——代数方程.

因此,问题转化为求代数式4x-5y的最小(大)值问题.

因为以上关于x的一元二次方程有实数根,所以Δ= 64t2-4×25(t2-225)≥0,解得-25≤t≤25.
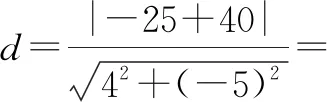
解后反思:判别式法的本质就是将(解析)几何问题转化为代数问题,通过整体化思维,引入参数并转化对应的直线与椭圆的方程之间的关系;利用函数与方程思想,结合代数方程的构建,借助一元二次方程有实数根来合理构建对应的不等式达到确定对应参数取值范围的目的,结合参数的端点取值情况来确定对应的最值.
方法3:三角换元法——参数方程.



解后反思:三角换元法的本质就是依据曲线的参数方程的等价转化,合理进行三角换元并变形,将平面解析几何问题并转化为对应的三角函数问题;结合椭圆上的点到直线距离的确定,借助三角函数中的三角恒等变换公式,特别是辅助角公式的应用,为利用三角函数的有界性来确定最值问题提供条件.借助平面解析几何中圆锥曲线参数方程的三角换元,利用参数方程来处理此类问题,更加简捷有效.
3 链接高考
涉及椭圆上的点到其他点、直线等的距离的最值问题,也是高考中常见的一类热点问题.借助椭圆参数方程的构建与转化,将平面解析几何问题转化为对应的三角函数问题,结合三角函数来分析与处理,简单快捷.
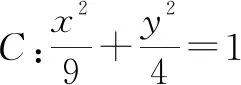
A.13 B.12 C.9 D.6
参考答案:C.
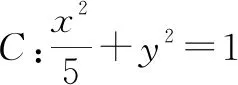
参考答案为:A.
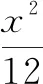
高考真题4(2023年高考数学全国乙卷文科·11)已知实数x,y满足x2+y2-4x-2y-4=0,则x-y的最大值是( ).
解析:由x2+y2-4x-2y-4=0,配方可得
(x-2)2+(y-1)2=9.



总评:引入圆的参数方程进行三角换元,构建对应的三角函数关系式,利用三角函数的有界性来确定对应的最值问题.参数方程背景下的三角换元法处理是破解圆锥曲线问题中比较常用的一类技巧方法,特别是将最值问题转化为三角函数的相关问题来处理,更加有效.
4 教学启示
4.1 方法总结,技巧归纳
解决一些涉及圆锥曲线上的点所对应的代数关系式的最值或取值范围问题,常见的呈现方式有线段的长度、点到直线的距离、直接代数关系式等,常见的破解方法有切线平移法——数形结合、判别式法——代数方程、三角换元法——参数方程等.
特别地,可以巧妙引入圆锥曲线的参数方程,利用参数方程表示有时比用普通方程更简捷方便,巧妙将(解析)几何问题转化为三角函数问题,借助三角函数知识,灵活求解相应的最值或取值范围等问题.
4.2 回归教材,挖掘内涵
高中数学教材中的例(习)题等,都是几代教育与教研工作者在不同时代、不同岗位下智慧与教研的精华沉淀与传承积累,具有良好的典型示范与引领作用.借助教材例(习)题,充分挖掘基础知识、基本内涵,剖析知识的展示、应用以及思维方法的技巧与综合,延续良好的传承与发展.
在平时数学教学与学习过程中,不要脱离高中数学教材,应以教材为蓝本,以本为本,全面吃准吃透教材中的例(习)题、探究、思考、阅读等各方面的内容,合理挖掘本源,为知识的理解与掌握、能力的巩固与提升提供强有力的基础与动力.

