化韦达定理“无效”为“有效”的策略*

云南省曲靖市第一中学 张国坤 董善清

1 韦达定理有效与无效情形分析

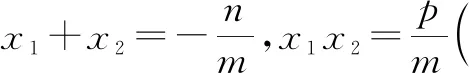
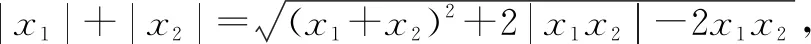
但有时会遇到“无法”处理的情形,譬如遇到将问题化归为λx1x2+μx1+rx2+q的情形,当μ≠r时,对μx1+rx2就“无法”使用韦达定理处理,问题“摆不平”,此时韦达定理就“失效”了.

2 韦达定理变“无效”为“有效”的策略

当遇到λx1x2+μx1+rx2+q(μ≠r)这类情形时,可以实施如下程序化的策略尝试处理.

2.1 降幂:“两根之和”与“两根之积”间的代换

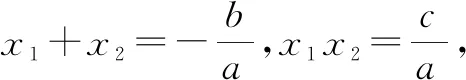
2.2 消元:利用“两根之和”进行根间代换

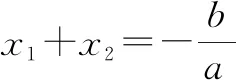
利用韦达定理降幂和消元常常可以使问题顺利求解,利用韦达定理的变式降幂和消元就是使韦达定理变“无效”为“有效”的有效策略.

3 韦达定理变“无效”为“有效”的策略应用举例

下面通过几道例题的解析,展示变式利用韦达定理进行降幂、消元而让韦达定理变“无效”为“有效”的运用策略.

3.1 变式利用韦达定理进行和积代换

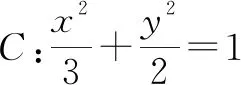
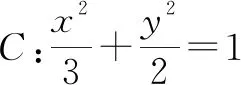
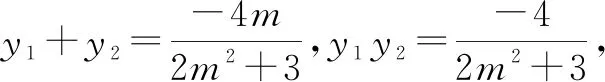
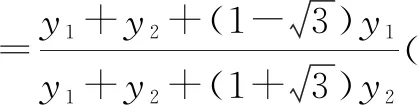
所以,直线AD,BE的斜率的比值等于定值.

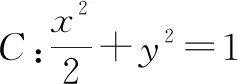
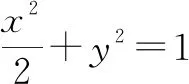
(1+2k2)x2+8kx+6=0.

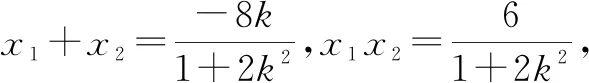
设直线AM,BN的交点为P(x,y).由直线l与y轴不重合,得x≠0.

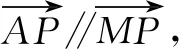
(y1+1)x-x1y=x1.

①

(y2-1)x-x2y=-x2.

②

联立①②,解得

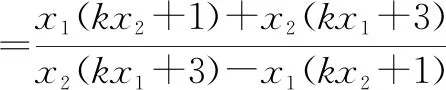
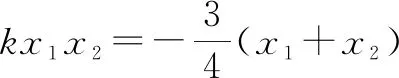
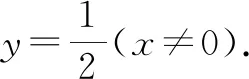
3.2 利用韦达定理进行和积代换与根间代换

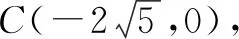
(1)求C的方程.

(2)记C的左右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于M,N两点,M在第二象限,直线MA1与NA2交于P,证明:点P在定直线上.

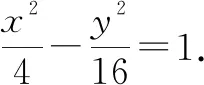
设M(x1,y1),N(x2,y2),已知M在第二象限,则y1>0,y2<0,x1<0,x2<0.由韦达定理,得

两式相除,得2my1y2=3(y1+y2).

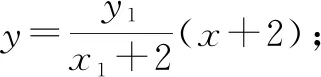
将x1=my1-4和x2=my2-4代入上式,化简整理,得

所以,直线A1M与直线A2N的交点P在定直线x=-1上.

本题解答中,看似必须使用韦达定理,但韦达定理失效了,联合使用韦达定理的“两根之积”与“两根之和”得到y1y2与y1+y2的关系式2my1y2=3(y1+y2),将y1y2降幂处理,问题瞬间化险为夷.

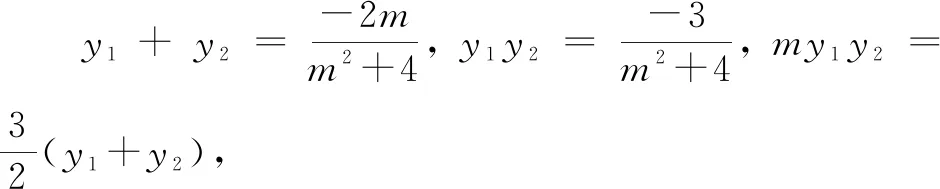
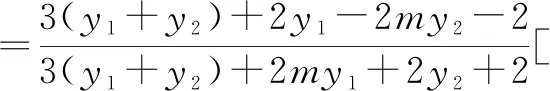
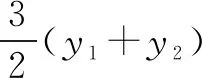
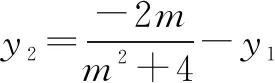
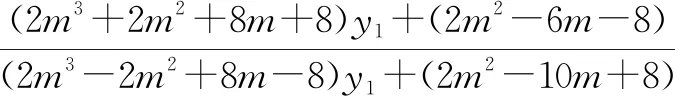
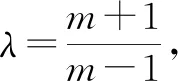
4 总结