双连杆柔性关节机械臂分数阶线性自抗扰控制*

陈志环,戴雪刚,董加顺

(武汉科技大学 a.冶金自动化与检测技术教育部工程研究中心;b.机器人与智能系统研究院,武汉 430081)

0 引言

柔性关节机械臂(flexible joints manipulator,FJM)因质量轻,灵活性好,能耗低等特点,广泛应用于航天、医疗领域[1-2]。由于机械臂的关节存在柔性,其系统更为复杂,从而系统会受到柔性振动的干扰。机械臂除了自身振动外还受到外界扰动的影响,这就要求控制器需要提供更高的控制性能。因此对FJM控制器的设计进行深入研究具有重要意义和实际应用价值。

为了有效地解决上述问题,不少学者围绕柔性机械臂的控制问题展开了一系列的研究,一些控制策略被相继提出并得到了很好地验证。汪允鹤等[3]引入了一种基于饱和函数的滑模变结构控制方法,实现了在一定的系统特性下沿规定的状态轨迹作小幅度、高频率的上下运动的鲁棒控制,从而使FJM系统具有更好的控制精度及稳定性。ZHONG等[4]提出了一种基于滑模控制策略和非线性扰动观测器的双边控制器,通过扰动观测器来估计FJM的模型不确定性和外部扰动,并补偿了系统的控制输入,有效地衰减了外部干扰对系统的影响。张丽娇等[5]为了衰减FJM受干扰的程度以及逼近系统的不确定性,引入了鲁棒控制项,所设计的控制方案能够明显地提高了系统的鲁棒性。

上述的控制方法大多适用于精确的机械臂模型,然而机械臂在复杂的环境中工作会受到内、外部因素的影响,如系统摩擦、机械磨损等,以上的因素都会导致机械臂模型的不精确。为了不依赖于机械臂的数学模型,因此一些学者在机械臂控制系统中引入LADRC的方法。但传统的LADRC因控制要求的提升,也凸出了一些自身的不足。LIN等[6]指出LADRC难以获得比例微分增益的值,提出一种基于误差的可变增益线性自抗扰控制器,仿真结果验证了抗扰性、快速性优于传统的LADRC。ZHOU等[7]指出了传统的LADRC在面对高阶系统或时滞系统时无法获得更好的控制性能,因此引入了一种基于观测器带宽近似IMC控制器的方法,调谐后的LADRC性能更佳。近些年,随着分数阶理论的不断地完善,分数阶控制器相对于整数阶控制器有着更优的动态性能和鲁棒性,因此将分数阶控制器与自抗扰控制器结合,融合各自的优势,已经在某些方面得到了很好地验证。CHEN等[8]在PMSM伺服速度系统引入了分数阶自抗扰控制,相对于整数阶自抗扰控制,该系统具有更好的速度响应性能和鲁棒性。

综上所述,本文针对柔性关节机械臂中较为常用的双连杆柔性关节机械臂的柔性振动和受外部干扰问题,提出了一种复合控制器策略。本文的主要贡献如下:

(1)针对双连杆柔性关节机械臂系统,采用奇异摄动法进行解耦,分解成具有多时间尺度的两个子系统,然后分别对代表刚性部分的慢速子系统和代表柔性部分的快速子系统进行控制,解决了由柔性关节和刚性臂杆的刚柔耦合所带来的高性能控制器设计的难题。

(2)相对于传统的线性自抗扰控制器,本文所提出的分数阶线性自抗扰控制器能较好的抑制柔性振动和外部干扰,通过结合快速子系统的微分补偿项,系统的控制性能更佳。

1 背景介绍

1.1 分数阶线性自抗扰控制

分数阶线性自抗扰控制器(fractional order LADRC,FOLADRC)将分数阶控制器与线性自抗扰控制器结合,将线性自抗扰控制反馈控制器的整数阶PD控制替换成分数阶PDμ控制。当μ在(0,1)之间时,就是具有更好控制效果的分数阶控制器,而μ=1时就退化成线性自抗扰中的整数阶PD控制器。FOLADRC的结构如图1所示。

图1 分数阶线性自抗扰控制器

图1中,FOLADRC主要由以下3个部分组成:跟踪微分器(tracking differentiator,TD)、线性扩张状态观测器(linear extended state observer,LESO)、线性状态误差反馈控制律(linear state error feedback,LSEF)。TD为输入信号安排过渡过程,得到光滑的输入信号以及各阶微分信号。然后根据系统模型确定LESO的阶数,LESO要比系统模型高一阶,系统总扰动的状态作为LESO的最高阶次。最后,根据LESO估计的系统状态设计LSEF,从而保证系统能根据设定值进行调整,最后要对扰动进行补偿消除。分数阶线性自抗扰控制器既保持线性自抗扰控制可以估计补偿内外干扰的特点,同时由于增加了两个调节自由度,可以使系统调节范围更广,能更好的抑制外界扰动和减弱柔性振动。

1.2 Oustaloup算法及其改进算法

为了实现分数阶控制器的控制律,选定拟合频率段,在该频段内实现分数阶微分算子的近似计算,Oustaloup滤波器的表达式为:

(1)

(2)

由于式(2)中常规的Oustaloup算法在逼近的频率高低段拟合效果不好,而改进的Oustaloup算法[9]通过引入适当的系数,可以大幅度地改善近似频率段两端的逼近效果。改进的Oustaloup滤波器本身采用分数阶近似,其传递函数为:

(3)

式中:b>0,d>0,s=jw,0<α<1。

在频率段内将式(3)使用泰勒展开,并取一阶近似,可得:

(4)

确定拟合频段为[0.001,1000],α=0.6,逼近阶次N=5。通过经验确定改进Oustaloup算法中的参数b=10,d=9。因此可以得到两种算法的频率响应曲线,如图2所示。

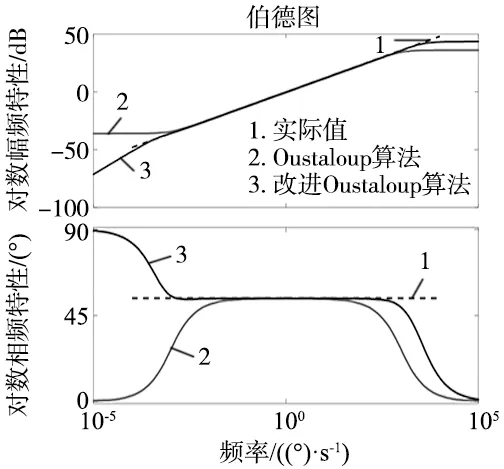
图2 频率响应曲线

由图2可知,相对于原算法,改进的Oustaloup算法可以更好地逼近频率段两端,从而使系统的控制效果更佳。因此本文的分数阶系统采用的是改进的Oustaloup算法。

1.3 柔性关节机械臂动力学模型

建立如图3所示的柔性关节和刚性臂杆相结合的双连杆柔性关节机械臂(dual linkage FJM,DLFJM)动力学模型。

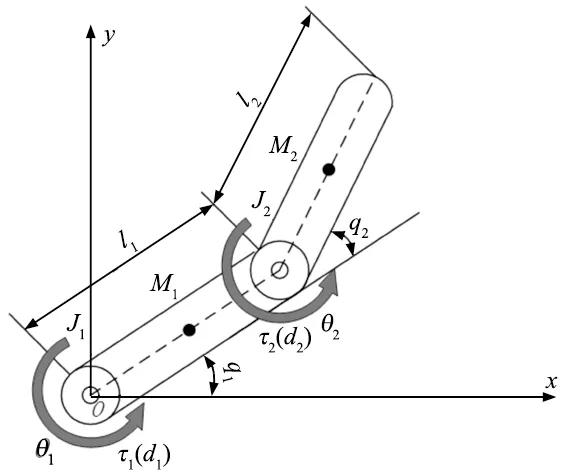
图3 双连杆柔性关节机械臂

图3中,惯性坐标系xoy下的DLFJM参数为:θ1和θ2分别为关节电机1和电机2的旋转角度,q1为连杆1的旋转角度,q2为连杆2相对于连杆1的旋转角度,l1和l2分别为连杆1和连杆2的长度,M1和M2分别为连杆1和连杆2的质量,m1和m2分别为关节1和关节2处电机和负载的质量,J1和J2分别为关节电机1和关节电机2转动惯量,τ1和τ2分别为关节电机1和关节电机2的输入扭矩,d1和d2分别为机械臂的未知外部干扰。

DLFJM的总动能由臂杆动能和关节动能组成,T1和T2分别为总臂杆动能和总关节动能。

(5)

(6)

则DLFJM的总动能T为:

T=T1+T2

(7)

系统的总势能P由连杆及其负载势能组成:

(8)

将式(7)和式(8)代入到拉格朗日方程中,可得DLFJM的动力学方程为:

(9)

根据图3所示的机械臂结构,两个关节力矩可以表达为:

(10)

式中:Ki代表关节i的刚度。

根据式(10),将式(9)进一步推导为:

(11)

2 快慢速子系统控制器

慢速子系统描述了刚性机械臂转动的过程。通过设计分数阶线性自抗扰控制器可以更好地抑制转动过程中的外界扰动和柔性关节的弹性振动。快速子系统描述了柔性关节弹性振动的过程。通过设计微分补偿器来削弱系统的振动。则DLFJM的快慢速子系统组合控制器的原理可如图4所示。

图4 快慢速子系统组合控制原理

2.1 模型分解

柔性关节和刚性臂杆的刚柔耦合提高了控制器的设计难度,因此使用奇异摄动法对DLFJM解耦,使其分解成代表刚性部分的慢速子系统和代表柔性部分的快速子系统。

定义弹力力矩矩阵P,选择P和连杆转角q分别为两个子系统的快、慢变量,令关节刚度系数K=K1/ε2,ε为很小的摄动常值,则:

P=K(θ-q)=K1(θ-q)/ε2

(12)

将式(12)代入到式(11)可得:

(13)

(14)

式中:τ为慢速子系统控制律τs和快速子系统控制律τf之和,则τ=τs+τf。

(15)

令上式中值为0,可得式(15)的根为:

(16)

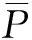
(17)

(18)

(19)

将式(17)和式(19)简化,可得DLFJM系统的奇异摄动形式的表达式为:

(20)

(21)

式(20)为解耦出的代表刚性部分的慢速子系统,式(21)为代表柔性部分的快速子系统。通过设计两式中τs和τf来实现机械臂的轨迹跟踪控制。

2.2 慢速子系统控制器

为了方便控制器的设计,将式(17)写成状态空间表达式的形式:

(22)

分数阶线性自抗扰的线性状态观测器可以估计电机摩擦等影响系统性能的内外干扰,针对式(17)所示的二阶系统设计三阶LESO为:

(23)

而分数阶线性自抗扰控制器的控制律为:

u=u0-z3

(24)

式中:u0的设计采用分数阶PD控制,具体表示为:

(25)

加入前馈控制量的线性控制律设计如下:

(26)

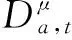
2.3 快速子系统控制器

式(21)为快速子系统的微分方程,该方程中缺少Pf的一阶微分项,因此系统是不稳定的。为了使系统稳定,可以采用如下线性修正项[12]:

(27)

将式(27)代入式(21)中,使原快速子系统的阶数完整,通过设定合适参数可以使快速子系统稳定。

综合式(26)～式(27)的设计,得到了快慢速子系统的组合控制律τ=τs+τf,从而有效地解决了刚柔耦合的DLFJM系统所需的高性能控制器设计难题。

3 数值仿真验证与分析

为了评估本文所提出的复合控制器性能,对DLFJM的轨迹跟踪进行仿真实验。通过以下3组实验来体现本文所提出的复合控制器的控制效果:快速子系统的微分补偿项削弱系统抖动实验、分数阶LADRC和整数阶LADRC对比实验以及验证所提分数阶LADRC抗扰性能实验。双连杆柔性关节机械臂系统动力学参数如表1所示。

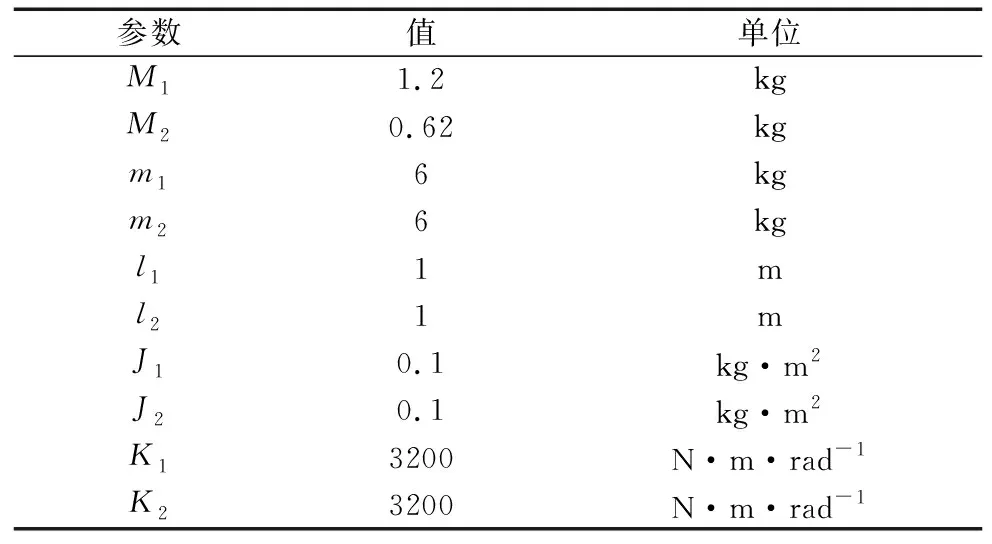
表1 双连杆柔性关节机械臂参数

设置分数阶线性自抗扰控制器的参数与线性自抗扰控制器的相关参数相同,具体参数如表2所示。

表2 各连杆控制器参数

3.1 快速子系统线性补偿实验

为了验证微分修正补偿对系统振动的削弱作用,通过上述系统参数,设定不同的Kf,对所设计的控制器进行仿真对比实验,通过杆1和杆2的跟踪曲线进行分析。两连杆的跟踪轨迹为qdes1=qdes2=sin(πt),仿真时间为5 s。

图5为连杆1和连杆2在Kf=0.5、Kf=10下的轨迹跟踪图。由图可知,连杆1在Kf=0.5出现了轻微抖动,但相对于Kf=10下轨迹跟踪的抖动较为明显,然而连杆2的轨迹跟 踪是叠加了杆1控制器的作用,因此在微分补偿项较小时,即Kf=0.5下抖动大,两连杆在1 s后由于分数阶线性自抗扰的作用,连杆轨迹能很好的跟随设定轨迹,达到轨迹跟踪的目的。

图5 不同Kf作用下的连杆轨迹跟踪

3.2 分数阶LADRC和LADRC对比实验

为了验证分数阶LADRC跟踪轨迹的优越性,采用3.1节实验相同的控制输入,分别使用FOLADRC控制器和LADRC控制器对DLFJM进行控制。

从图6a和图6b中的跟踪曲线和误差曲线可知,使用FOLADRC控制器和LADRC控制器对两杆的轨迹追踪效果都很好。但在臂杆启摆时,通过分数阶LADRC控制的两臂杆振幅小,且在0.3 s后,误差远小于使用LADRC控制的机械臂跟踪误差,证明通过增加的两个自由度,提高了系统的稳定性能。

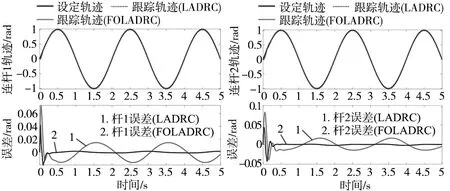
(a) 杆1的跟踪曲线和误差曲线 (b) 杆2的跟踪曲线和误差曲线图6 FOLADRC和LADRC的跟踪曲线和误差曲线

3.3 分数阶LADRC和LADRC抗扰实验

在3.2节实验中,FOLADRC取得了较好的跟踪效果。本节实验中将通过阶跃信号qdes1=qdes2=π/3来进一步地验证分数阶LADRC的跟踪特性,并在2 s后对两杆加入了阶跃频率扰动d1=d2=10,仿真时间为5 s。

图7为两连杆在设定轨迹的跟踪曲线图,图8为两连杆的误差跟踪图,表3为两种控制器作用的部分响应指标。从图7和图8和表3中可知,浅灰色曲线为FOLADRC,灰色曲线为相同参数下整数阶LADRC,采用LADRC控制器的调节时间和上升时间都大于使用FOLADRC的阶跃响应,体现了FOLADRC控制器可以更快地收敛到所需值的优越性。同时,使用LADRC存在超调,而FOLADRC的超调量为0,表明了FOLADRC控制器具有更好的稳定性。在2 s后加入持续的外界扰动,两种控制器都能很好地抑制扰动,但对于阶跃信号进行跟踪,使用FOLADRC在抑制外界扰动上要优于整数阶LADRC。

图7 加入外界扰动的位置响应曲线 图8 加入外界扰动的位置响应误差曲线

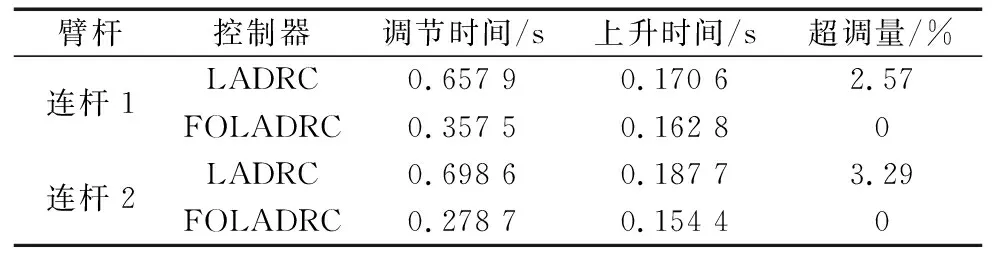
表3 控制器响应指标对比

4 结论

本文针对DLFJM的柔性振动和受外部干扰的问题进行了仿真实验,最终得到结论如下:

(1)快速子系统控制器能使DLFJM系统更加稳定,减少了系统的抖动,证明了快速子系统线性修正项补偿的重要性。

(2)分数阶线性自抗扰控制器相对于整数阶线性自抗扰控制器,超调量小,能更好的抑制外界扰动和减弱柔性振动。

接下来的工作是进行实物平台的搭建和实验,进一步验证本文所提的复合控制策略在实体机械臂中具有良好的轨迹跟踪性能。