数控机床可靠性加速试验与评估研究*

肖泽坤,夏仰球,滕 强,许耀宇,米 良

(1.中国工程物理研究院机械制造工艺研究所,绵阳 621900;2.国家机床产品质量检验检测中心(四川),成都 610000)

0 引言

数控机床作为支撑国民经济和国防建设的战略装备,是国家发展汽车、钢铁、军工和航空航天等行业的工业利器。目前国产数控机床在机械结构设计和数控系统优化等方面的研究已经取得了一定的成果,但运行过程中设备故障率偏高、先进功能保持性差等可靠性问题却一直存在[1]。

可靠性测评方法是制约机床可靠性水平提升的重要因素,高效准确的测评方法始终是业内学者聚焦的热点。传统可靠性评估多是基于现场跟踪统计收集到的机床的故障信息,统计过程往往时间较长。KELLER等[2]跟踪统计了35台CNC设备的现场运维数据,分别用对数正态分布和威布尔分布对机床可靠性进行建模,评估得到了机床的平均故障间隔时间(MTBF)。贾亚洲、张英芝等[3-5]分别对多台数控机床的现场故障数据进行一年以上的跟踪统计,提出了整机故障分布的数学模型,揭示了故障分布规律,为当下可靠性特征量的评估奠定了基础。

如今机床产品的设计也趋于成熟,各零部件的MTBF往往在几千甚至上万小时,这就使得许多故障无法在短时间暴露,长时间跟踪统计又无法适应新产品的迭代周期,近年来加速试验与快速评价技术应运而生。屠国俊、李隽等[6-8]分别对滚珠丝杠、导轨、刀库等关键功能部件开展了相应研究,为功能部件的加速试验评估提供了一系列新的方法。在对数控机床相关的加速试验与快速评价技术研究中,多是围绕功能部件开展的,对整机的研究相对较少。国家机床质量监督检验中心建立了加工中心快速可靠性模型,并起草了相应标准。陈衡等[9]基于加工中心故障失效机理设计了可靠性加载试验装置,并依据上述标准规定在样机进行了加载试验,通过对比早年的统计结果,验证了可靠性快速评价技术的科学性。赵钦志等[10]提出了基于失效征兆映射的数控机床可靠性快速试验原理与评估模型,为机床产品可靠性快速评估技术的研究开辟了新的方向。

由于数控机床种类众多、形式各异,目前行业内缺乏一种能够普遍适用各类数控机床的整机快速测评方法。针对以上问题,本文将提供一种基于逆幂律模型的数控机床可靠性快速试验与评估方法,使用电应力作为加速应力来表征机床所受的载荷水平,为数控机床可靠性快速评估提供一种新的解决途径。

1 数控机床可靠性快速评估方法

由累积损伤理论可知,在许用应力范围内,产品的工作时间长短与所受应力的高低直接相关。数控机床在渡过早期故障阶段之后,故障主要是由服役性能退化引起,也就是说机床产品的失效机理为累积损伤时,其可靠性指标直接取决于应力水平。根据这一原理,数控机床快速可靠性试验常采用试验载荷谱代替常规载荷谱,实现加速失效、缩短试验时间的目的,其次,再通过可靠性加速模型将试验条件下应力水平获得的可靠性指标等效为正常应力水平下的可靠性指标[11]。

1.1 加速模型

逆幂律模型是最常用的加速寿命模型之一,常被用于以疲劳、磨损为失效机理的机电一体化产品加速寿命试验。该模型使用电应力,如电压、电流或功率作为加速应力,通过提高加速应力来加速产品失效时间,其特征寿命与加速应力间的关系为:

ζ=AV-C

(1)

式中:ζ为特征寿命,A为常数,V为电应力,C为与激活能相关的常数。

1.2 修正应力计算

数控机床作为典型的机电液一体化产品,其失效模式众多,归结起来均是由外部载荷引起,本文拟用电应力来对机床载荷水平进行表征,如果单独将整机的电应力作为加速应力,通过逆幂律模型求解机床的可靠性指标往往会出现较大的偏差。对此,笔者基于层次分析法(AHP)以电功率为加速应力提供一种整机修正应力计算方法,步骤如下[12]:

步骤1:选定功率为加速应力确定目标,将数控机床按运动轴划分为多级子系统构建准则层,以受试数控机床作为方案层建立图1所示加速应力层次修正结构;

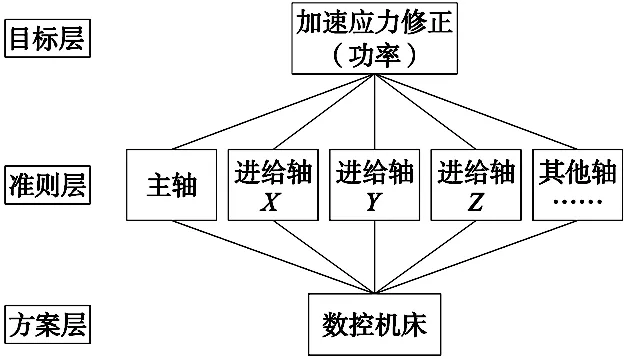
图1 数控机床加速应力层次修正结构

步骤2:利用萨德标度对准则层各运动轴功率的重要度进行比较,建立量化后的判断矩阵A;

步骤3:计算判断矩阵A最大特征值对应的特征向量W=(W1,W2,…,Wn)T为运动轴功率的权重向量,并完成一致性检验;

步骤4:根据得到的权重向量结合单轴功率进行加权得到修正后的整机功率:

(2)

式中:VP为修正后的整机功率,Wi为第i个运动轴功率对整机功率的影响权重,VPi为第i个运动轴的功率。

1.3 可靠性评估

逆幂律模型参数需要至少在两种加速工况S1和S2下进行求解,即依靠不同工况的应力水平及相应的特征寿命求解逆幂律模型参数,对于特征寿命的计算应遵循以下基本假设:

假设Ⅰ:受试机床产品在上述各应力水平下失效时间均服从威布尔分布;

假设Ⅱ:在正常应力水平下与上述各加速应力水平下受试机床产品失效机理相同,对应威布尔分布的形状参数m相等;

假设Ⅲ:受试机床产品的剩余寿命仅与已累积失效部分及当前应力水平有关,而与累积失效方式无关。

1.3.1 逆幂律模型参数

式(1)两边取对数,得:

lnζ=a+blnV

(3)

式中:a=lnA,b=-C。

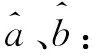
(4)

(5)

式中:V1、V2为加速工况S1和S2对应的加速应力水平,ζ1、ζ2为加速工况S1和S2对应的特征寿命。

1.3.2 加速系数

(6)

式中:Ki～0为应力水平Vi较常规应力水平V0的加速系数。

1.3.3 威布尔分布参数

常规工况S0下的威布尔尺寸参数θ、形状参数m按式(6)和式(7)进行计算:

(7)

(8)

式中:V0为常规工况S0对应的应力水平,m1、m2为加速工况S1和S2对应威布尔形状参数。

1.3.4 平均故障间隔时间

(9)

2 数控机床可靠性加速试验

2.1 试验方案

可靠性加速试验采用负载试验加空运行强化的方式,最大程度还原机床在工作时各部分所承受的载荷,以激发设备的潜在故障。应力水平由低到高依次进行负载试验,试验过程中对各运动轴电机的功率进行采集。采用定时截尾,对受试对象的运维情况进行跟踪统计。

2.2 试验流程

参照GB/T 23567.1-2009《数控机床可靠性评定第1部分:总则》有关规定,结合逆幂律模型求解试验要求,整体试验流程设计如图2所示。

2.3 试验剖面

试验剖面指可靠性试验中规定的条件。可靠性加速试验除鉴定试验剖面外还应有两个加速试验剖面。加速试验剖面的设计至关重要,试验应力取值过高,则可能对机床造成损坏;取值过低,则性能退化不明显,难以获取有效数据[13]。

结合逆幂律模型特点,以加速系数作为试验剖面设计的依据,各剖面下的加速系数推荐值如表1所示。

表1 加速系数推荐值

2.4 数据采集

试验数据的采集主要分为设备故障统计和运动轴电机功率测量。设备故障统计主要记录在加速试验期间设备运转和工作情况,如果发生故障,应该对故障时间、故障部位和故障模式等进行记录。运动轴电机功率测量用于定量衡量设备应力水平。功率测量的仪器是Fluke NORMA 5000高精度功率分析仪,如图3所示,通过连接驱动器动力线端子与仪器功率采集通道进行采集。

图3 运动轴电机功率采集

3 应用案例

根据上述可靠性评估方法与试验要求开展可靠性快速测评试验,受试对象为某型号国产数控弯管机,该型号设备共5台,其基本参数如表2所示。

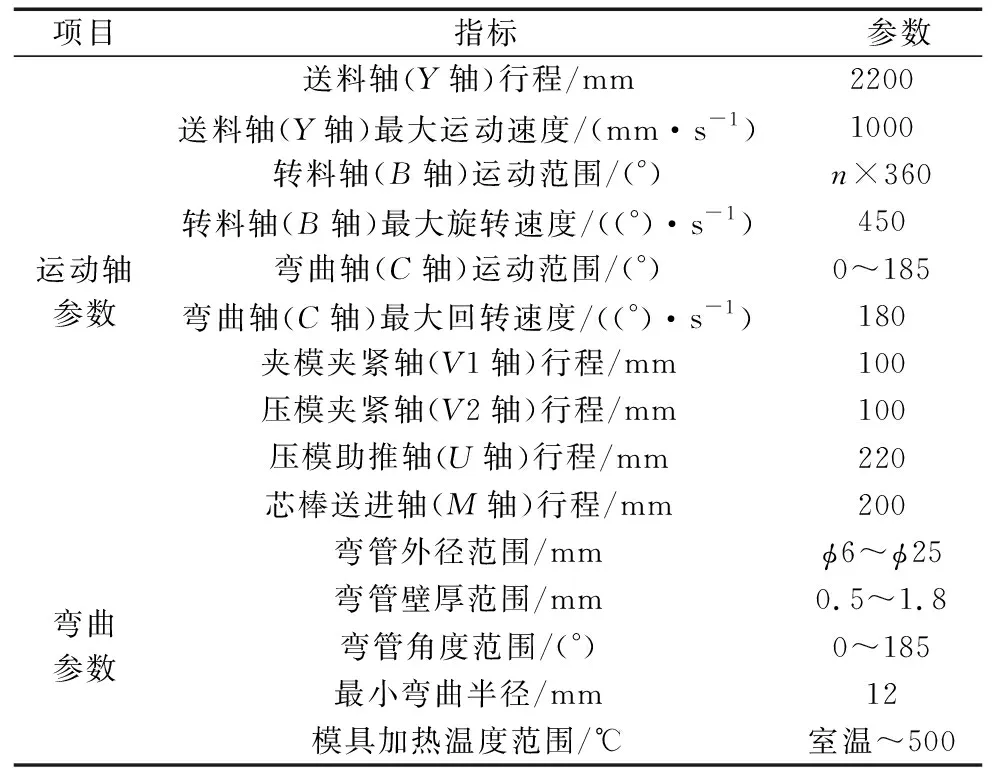
表2 数控弯管机主要技术参数

采用试验场试验的方式,设备负载运行方式如图4所示。

图4 弯管机负载运行试验

数控弯管机分为7个运动轴子系统,分别为:送料轴Y、转料轴B、弯曲轴C、夹模夹紧轴V1、压模夹紧轴V2、辅推轴U和抽芯轴M,采用专家打分的方式对各运动轴重要度基于电功率进行排序,建立判断矩阵:

根据判断矩阵A,各运动轴电机功率对数控机床整机功率的影响权重向量W=(0.529,0.156,3.194,1.573,0.985,0.343,0.22)。

将试验采集到的3种应力水平下各运动轴功率以均方根值代替,如表3所示。

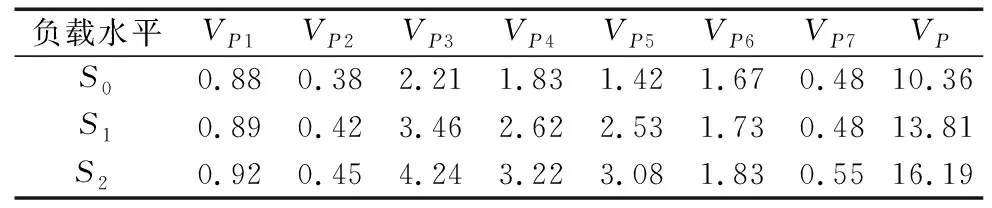
表3 运动轴功率均方根值 (kW)

根据式(2)分别计算各应力水平下修正后的机床功率如表4所示。

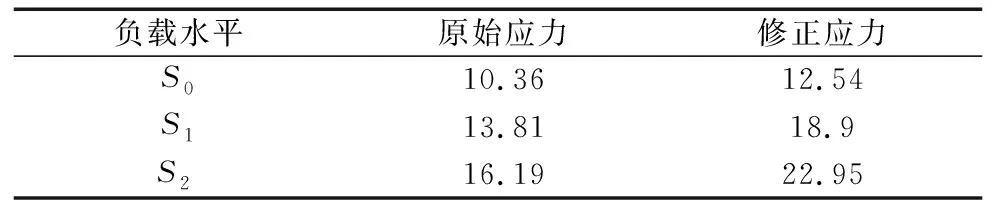
表4 机床修正应力结果 (kW)

试验共进行了700 h,其中设备在负载水平S1下运行400 h,负载水平S2下运行300 h,期间5台设备共发生15次故障,其故障分布统计如表5所示,其中负载水平S1下7次,负载水平S2下8次,故障时间分别如图5和图6所示。

表5 故障分布统计表

图5 负载水平S1故障发生时间 图6 负载水平S2故障发生时间

对两种负载水平下的故障数据分别进行最小二乘拟合,对拟合结果采用K-S检验后得到威布尔模型参数θ1=364.6,m1=1.22;θ2=242.47,m2=1.48。

将原始应力和修正应力值分别结合以上威布尔模型参数拟合值,代入式(4)～式(8)计算正常负载水平S0下的分布模型,并与项目组内同型号设备基于负载水平S0开展的现场跟踪统计1500 h结果进行比对,威布尔模型参数值如表6所示。

表6 不同方法的威布尔分布参数

利用表6中3种测评方法的威布尔参数分别绘制得到概率分布函数结果如图7所示。

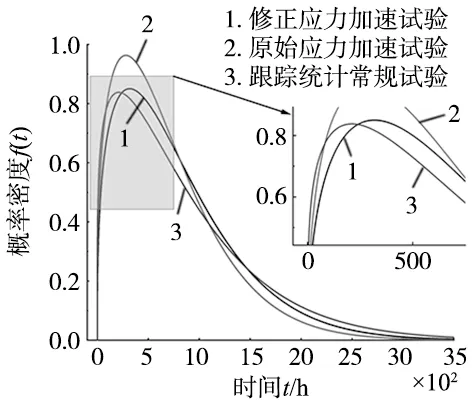
图7 不同测评方法威布尔分布模型对比

从图7中可以得出:

(1)采用修正应力的加速试验模型较未进行应力修正的模型与跟踪统计常规试验模型相比相差较小,威布尔参数的相对误差分别为4.7%和4.65%,说明本文提出的修正应力具有有效性。

(2)基于逆幂律模型的两种评估方法计算得到平均无故障时间MTBF值分别为791.6 h、698.95 h,与传统测评方法841.07 h相比,相对误差为5.9%和16.9%,可以看出修正应力的测评结果更接近实际。

4 结论

(1)结合疲劳累积损伤理论,总结了可靠性快速测评试验原理,基于数控机床在不同的运行工况下,各运动轴载荷对整机贡献不同,并提出了应用层次分析法对各运动轴重要度进行赋权,以此进行应力修正。

(2)提出了基于逆幂律模型的数控机床可靠性快速测评方法,以此设计了试验流程、剖面以及数据采集方式,寿命模型中加速应力采用修正应力结果进一步提高了评估精度。

(3)在某国产数控弯管机上进行了加速试验与可靠性评估,通过应用AHP方法对试验数据中的加速应力进行修正,得到的威布尔形状参数误差为4.7%,可靠性指标MTBF的相对误差为5.9%,验证了本方法的准确性。