智能变电站风险评估方法研究

闫佳文,周 磊,蒋春悦,陈长金,刘 哲

(1.国网河北省电力有限公司培训中心,河北 石家庄 050031 ;2.北京科东电力控制系统有限责任公司,北京 100192)

0 引言

计算机、网络、大数据、物联网、通信等技术[1-2]的不断发展为智能电网[3]的改革与创新带来了契机,特别是为智能变电站[4-6]系统的监控、状态运行评估等奠定了基础。作为典型电网的核心部分,输配电变电站在向用户输送优质电力和控制潮流方面发挥着重要作用。为了保证一次设备的安全和稳定运行,对继电保护系统(relay protection system,RPS)的运行状态进行风险评估很有必要。

近年来,RPS运行状态的风险评估已成为热门研究课题,大量学者对其进行研究并取得了丰硕成果。目前,有两种主流的评估方法。其一为模拟方法,如蒙特卡罗模拟法[7]。模拟方法主要通过统计分析和假设概率分布的随机抽样来获得可靠性指标。该方法实现简单但评估精度较低。其二为分析方法,如马尔可夫模型分析[8]、神经网络[9]、故障树[10]、层次分析法[11]等。分析方法通常需要考虑对象的逻辑关系,并通过迭代计算可靠性指标。分析方法结构清晰、精度较高,计算负担随着系统规模的增加而迅速增加。

本文提出了一种新的智能变电站RPS风险评估方法。首先,本文基于系统运行数据、故障数据和网络消息信息以及马尔可夫模型,对保护系统各装置的运行状态进行评估。其次,本文基于复杂网络,对智能变电站二次系统的状态和风险进行评估。

1 基于马尔可夫模型的状态评估

为了实现智能变电站二次设备的状态评估和风险评估,本文对硬件结构和功能相同的设备进行了分类,从而基于马尔可夫模型分别计算保护装置(protection devices,PD)中母线局部放电、线路局部放电、主变压器局部放电、网络交换机、组合单元和智能终端设备的故障率。以下对马尔可夫模型和状态评估执行过程作详细介绍。

1.1 马尔可夫模型

本文基于马尔可夫模型的评估方法对上述六种情况进行了失效率分析。在评估局部放电的运行状态时,预测状态仅受当前状态的影响,与历史状态没有直接关系。因此,基于马尔可夫模型,有:

(1)

式中:P为状态转移矩阵;Pij为下一状态i依赖于当前状态j的概率,i,j=1,2,…,n,n为状态个数;Δt为时间步长。

此外,Pij满足以下条件:

(2)

本文令A为转移密度矩阵,则有:

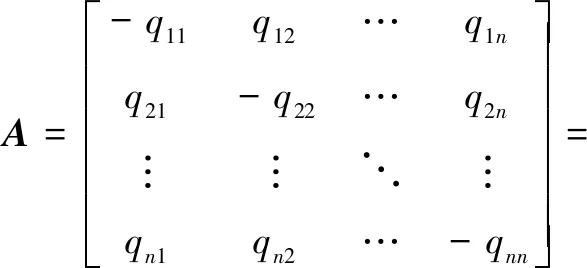
(3)

式中:qij为下一状态i依赖于当前状态j的概率密度函数;I为单位矩阵。

同理,qij满足式(4):

(4)

马尔可夫动态概率的行向量P(t)可定义为:

(5)

根据式(2),P(t)中所有元素的总和为1。根据转移密度矩阵A和马尔可夫动态概率的行向量P(t),对P(t)进行求导,可得出:

(6)

根据马尔可夫模型的特点,当时间t接近无穷大时,马尔可夫动态概率趋于稳定,则有:

(7)

1.2 状态评估执行过程

局部放电的状态由可靠性指标反映。可靠性指标的选择需要基本的可靠性数据支持。随着物联网、通信、网络等技术的成熟及智能变电站技术的飞速发展,二次设备的感知方法越来越丰富。因此,通过收集变电站的基础数据,如故障信息管理系统、检修报告、现场运行维护信息等,可分析设备运行状态。为此,本文提出了一个三状态的状态转移模型(正常-异常-故障),以描述系统可靠性指标。三状态的状态转移模型如图1所示。

图1 三状态的状态转移模型

由图1可知,PD故障由两个原因引发。其一为设备异常。设备异常主要指未及时修复设备导致设备功能失效,随即设备转入故障状态。其二为突发故障直接导致设备功能失效。

此外,局部放电的异常状态可分为两种。一是局部放电异常。该异常可由监控系统或人工操作进行检测,且可通过修复使系统重新恢复正常运行状态。二是无法发现装置的异常情况。这会导致时间累积后的局部放电故障。

由于影响PD有效运行状态的因素很多,为简化计算过程,本文所涉及的局部放电包括以下几个主要因素,即硬件、软件、外部环路和通信。设备各状态关系如图2所示。

图2 设备各状态关系图

图2中: ES0为设备的正常运行状态;AS1、AS2和AS3为局部放电的硬件、软件、外部电路和通信的异常运行状态,且这些异常状态均可通过监测发现;AS4、AS5和AS6分别为局部放电的硬件、软件、外部电路和通信的异常运行状态,且这些异常状态均未通过监测发现;IS7为设备的故障运行条件。

为有效分析系统运行,本文作如下定义。

定义1 显性异常概率。系统中PD存在异常。这些异常被检测到的概率称为显性异常概率,可通过式(8)计算:

(8)

式中:Y1、Y2、Y3为显性异常概率;T为保护系统的累计运行时间;n1、n2和n3为监控系统检测到的PD硬件、软件、外部电路和通信异常的次数。

定义2 隐性异常概率。系统中PD存在异常。这些异常未被检测到的概率称为隐性异常概率,可通过式(9)计算:

(9)

定义3 保护系统故障概率。保护系统的故障概率是由PD的异常运行(包括故障和拒止)引起的,计算式为:

(10)

式中:nW4、nW5和nW6分别为局部放电硬件、软件、外部电路和通信异常引起的局部放电故障次数。

定义4 局部放电失效概率。局部放电失效概率是由设备或组件突然失效引起的,可由式(11)计算:

(11)

定义5 异常修复概率。保护系统异常后的修复概率计算式为:

(12)

式中:TF1、TF2和TF3分别为设备硬件、软件、外部电路和通信异常的平均修复时间。

定义6 故障修复概率。PD故障后的修复概率由式(13)给出:

(13)

式(3)中的转移密度可计算如下:

(14)

(15)

综合上述方程,马尔可夫稳态概率P(∞)为:

(16)

因此,保护系统的三种状态的概率可计算如下:

(17)

式中:PES为正常状态运行概率;PAS为异常状态运行概率;PIS为故障状态运行概率。

2 基于复杂网络的风险评估模型

由于智能变电站二次设备的连接更加紧密,本文将二次设备系统视为一个复杂网络,并基于复杂网络理论对保护系统的运行风险进行评估。智能变电站RPS风险评估过程如图3所示。

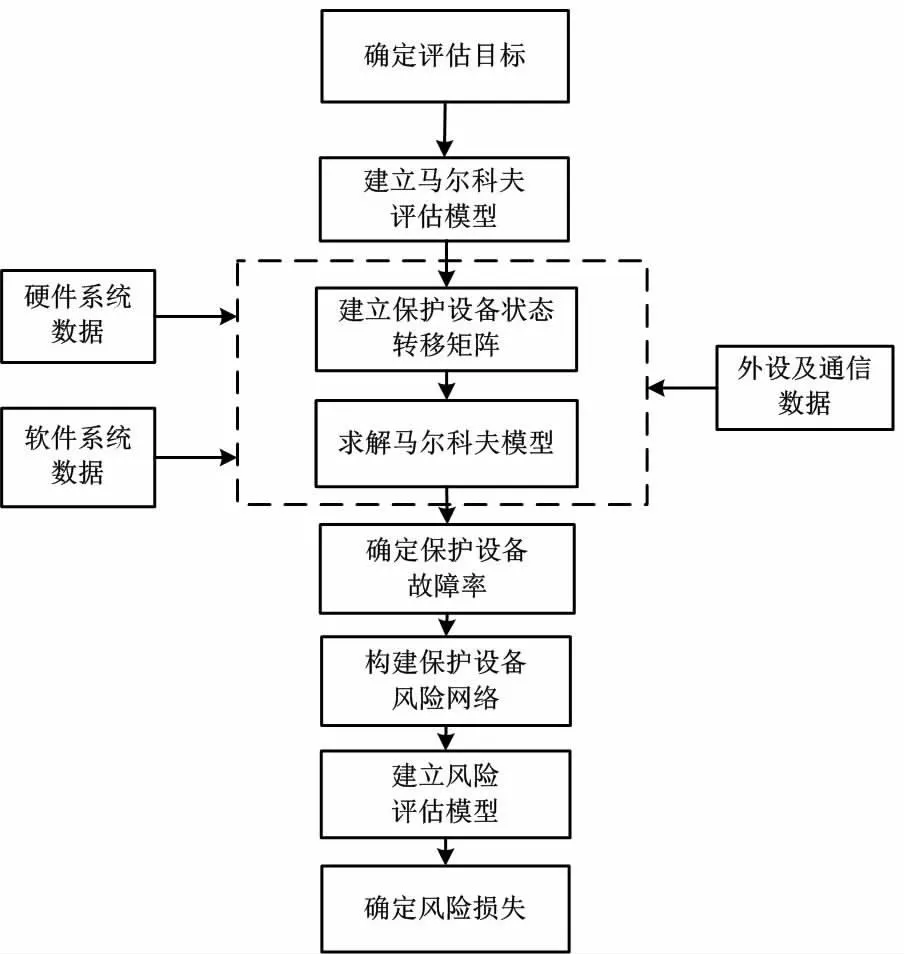
图3 智能变电站RPS风险评估过程图

2.1 相关概念

本文对风险网络建立过程中涉及的相关概念进行介绍。

定义7 网络节点。对于220 kV系统,保护系统中的PD、组合单元、智能终端、智能变电站网络的设备(如交换机、光纤和集线器等)均为网络节点。

定义8 智能体。网络中,智能体的定义为实现某种网络功能的网络节点。由于线路组合单元参与线路保护功能,故线路组合单元是线路保护功能的智能体。此外,本文将网络节点n中具有保护功能的智能体定义为Mni。其中,i为隶属度函数计算的度。

定义9 智能体集。保护系统中每个保护功能的实现都由多个智能体协同完成。因此,参与完成同一网络功能的所有智能体统称为智能体集。智能体集通常用S表示。

定义10 有向边。保护系统的每个保护功能均由多个智能体实现。这些智能体通过有线或无线方式彼此交互,并且信息的传输具有方向性。因此,智能体之间的定向信息交互称为有向边。

定义11 度。风险网络的度定义为参与完成保护功能的数目。例如,线路组合单元参与完成线路保护和母线保护,因此线路组合单元的度为2。

定义12 风险传递。保护系统的风险传递指:保护系统某一功能的实现需要由智能体集中的所有智能体串联完成,如果其中一个智能体失败且功能无法实现,则参与保护功能的智能体集将存在无法实施有效保护的风险。具体而言,某个电力单元(智能体)的故障将直接影响与其组合串联的其他电力单元(智能体),而不会影响没有与故障单元连接的其他电力单元(智能体)。风险传递的主要作用是去除随机现象,从而简化电力风险评估模型。例如,正线保护功能由合线单元、智能终端、PD、网络交换机等组成。当组合单元故障,即线路保护采样故障导致线路保护功能故障时,线路组合单元故障的风险并未转移到母线和主变压器的保护功能上。

基于以上概念,风险网络结构如图4所示。

图4 风险网络结构示意图

2.2 风险评估

在相关概念基础上,本节详细介绍了RPS风险评估模型的建立过程。变电站RPS的正常运行是保证一次设备和电网稳定、安全运行的基础。RPS故障会损坏相应的一次设备。RPS功能失效会影响二次系统本身和一次设备。因此,RPS的保护功能S的总风险式可描述如下:

RPS=R1+R2

(18)

式中:R1为S引起的一次设备风险;;R2为S对RPS造成的风险。

(19)

式中:PMi为S中第i个智能体的故障概率;CMi为S中第i个智能体故障造成的损失,可根据设备的维护成本进行计算;n为智能体集S中包含智能体的总数。

此外,本文假设只有当一次设备的所有保护功能失效且变电站在某时间间隔内发生故障时,保护系统故障才会导致一次设备损失。

(20)

式中:P1为一次设备发生故障的概率;C1为一次设备的风险损失,可通过一次设备的维护损失和停电损失计算;k为参与主要设备保护的S中非竞争性智能体的数量。

3 仿真与数值分析

3.1 数据集

本节以中国西部某智能变电站中典型220 kV母线连接模式为例,评估RPS的可靠性和风险。试验所用数据主要于2014年1月至2019年12月收集,具体包括保护系统所有二次设备的运行和维护记录、异常报警信息和一些其他数据(如异常时间、次数等)。智能变电站保护设备配置如图5所示。

图5 智能变电站保护设备配置图

智能变电站中,220 kV母线连接方式主要包括线路、母线、主变压器和母差。根据前述定义,线路组合单元为线路保护智能体,母差组合单元为母差保护智能体,高压/低压主变压器组合单元为主变压器保护智能体。同时,保护系统的每个保护功能由多个智能体共同实现。此外,采用网络采集和网络跳变方式的智能变电站,主要由保护系统中的PD和智能站辅助装置组成。其中,智能辅助设备主要包括组合单元、智能终端、网络交换机等。需要注意的是,为简化模型,智能变电站保护设备均遵循风险传递规则。

3.2 状态评估分析

仿真参数设置为:智能变电站二次设备的成功检测概率为0.9;局部放电硬件的平均修复时间一般为12 h;局部放电软件异常的平均修复时间一般为8 h;外部电路和通信异常的平均修复时间为24 h;局部放电系统故障后的平均修复时间为48 h。因此,根据修复概率定义:F1=0.833;F2=0.125;F3=0.041 7;F4=0.020 8。此外,仿真时除线路组合单元度设置为2,其他组合单元度均设置为1。

根据图5,以及所有线路、母线、主变压器、母差组成的保护系统所有二次设备的数据统计信息,保护系统参数如表1所示。表1中数据可根据式(9)～式(13)计算。

表1 保护系统参数

保护系统运行统计结果如表2所示。

表2 保护系统运行统计结果

表2中:PES为正常状态运行概率;PAS为异常状态运行概率;PIS为故障状态运行概率。仿真结果符合实际,表明所提马尔可夫模型能够有效模拟系统运行状态。

3.3 风险评估及分析

风险评估过程为:首先,根据风险评估过程,计算每个PD的失效概率;然后,建立变电站保护系统的风险网络,确定各保护功能的智能体集。此外,本文设线路间隔故障概率为0.000 5、主变间隔电网故障概率为0.000 23、母线故障概率为0.000 1。

根据式(17),保护系统故障率和风险损失统计如表3所示。

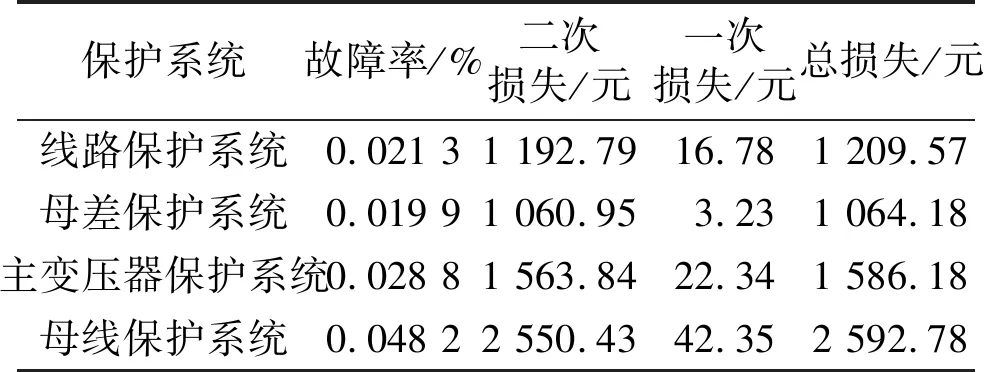
表3 保护系统故障率和风险损失统计

由表3可知,母线保护的二次风险损失在所有保护系统中最高,其次是主变压器保护,最后是线路保护和母差保护。经分析,二次风险损失中线路保护系统大于母差保护系统造成的损失的原因为:母差保护系统仅在母线充电过程中投入运行,其实际运行时间不太可能发生故障,由此造成的二次风险损失小于线路造成的二次风险损失。

3.4 综合对比

本节将所提基于马尔可夫模型的智能变电站风险评估方法与概率神经网络[9]、故障树[10]、层次分析法[11]等方法进行对比。对比指标选择“故障评估误差”和“是否可计算二次风险损失”。不同方法综合性能对比结果如表4所示。

表4 综合性能对比结果

由表4可知,所提模型识别误差为0.162 4%,且可计算二次风险损失。文献[10]所提基于故障树的方法虽然也能计算二次风险损失,然而故障树方法需要事先收集大量数据,且完全依赖于先验知识。因此,故障建模的好坏将对故障评估结果产生重大影响,且模型泛化性较弱。仿真结果进一步验证了所提模型对电力风险评估具有一定借鉴意义。

4 结论

本文基于马尔可夫模型和复杂网络理论,对智能变电站状态和风险评估进行了研究。由于在评估局部放电的运行状态时,预测状态仅受当前状态的影响,而与历史状态没有直接关系,本文提出了一种基于马尔可夫模型的智能变电站风险评估方法。同时,本文提出了一个三状态的状态转移模型(正常-异常-故障),用于描述系统可靠性指标。所提方法为智能变电站运行状态评估以及异常、故障风险评估提供了借鉴。未来可对数据安全进行研究,以进一步提升数据保护及网络攻击防护能力。