基于Hurst指数的PID控制参数优化

单港生　王志国　刘飞

摘 要 为了提高PID控制过程的控制性能，提出一种基于Hurst指数的PID参数优化方法。首先，给出基于Hurst指数的控制性能评价方法。然后，以Hurst控制性能指标为基础，结合绝对误差积分和控制作用限制项来定义PID参数优化的目标函数，使用遗传算法来求解PID参数值。最后，通过数值仿真和工业实例验证了该方法有效性。

关键词 PID参数优化 Hurst指数 控制性能评价 遗传算法

中图分类号 TP14   文献标识码 A   文章编号 1000?3932（2023）02?0158?07

基金项目：国家自然科学基金面上项目（61773183）。

实际工业过程中，组成控制回路的各个环节会随时间发生变化，这会导致控制系统性能相比投运初期出现下降，若不能及时监测到性能的变化并快速做出相應调整，将会造成经济损失或资源浪费［1］。控制性能优化技术是首先对控制回路性能进行评估，然后采用相应的措施改善控制性能。作为实际中广泛应用的PID控制回路，评价其控制性能并在性能不满足要求时通过校正PID参数以优化控制系统性能具有重要意义。

一般用于评价控制回路性能的指标有：确定性能指标、随机性能指标和鲁棒性指标。基于Hurst指数的控制性能评价指标属于随机性能指标。Hurst指数是HURST H E在研究尼罗河水文现象时提出的［2］，用来处理具有分形结果的时间序列，描述了时间序列的相关性。2012年，SRINIVASAN B等提出了在单变量控制系统中使用Hurst指数评价控制性能［3］，该方法不需要系统参数的先验知识，只需要系统的日常运行数据就能够准确计算出控制系统的性能指标。关于性能评价的研究可以追溯到20世纪，1989年，HARRIS T J利用系统过程数据和先验知识估计单变量控制系统的最小方差性能指标［4］。1997年，HUANG B等提出了滤波和相关性分析算法（Filtering and Correlation，FCOR），把单变量回路中的时延引申为关联矩阵，将最小方差性能指标推广到了多变量控制系统［5］。2002年，GRIMBLE M J提出了广义最小方差（Generalized Minimum Variance，GMV）基准，将控制输出作为惩罚项引入目标函数中，避免出现不切实际的大方差控制信号［6］。2003年，HUANG B提出使用线性二次型高斯（Linear Quadratic Gaussian，LQG）最优控制作为性能评估基准［7］，计算最优LQG控制律得到一条权衡曲线，系统的当前方差值越接近权衡曲线则控制性能越好。近几年来，学者们把基于时间序列分析的方法运用到了控制性能评价上。2014年，PILLAY N和GOVENDER P扩展了Hurst指数控制性能分析［8］，主要关注控制器设定点跟踪能力。2016年，DAS L等将基于Hurst指数的单变量系统控制性能指标与马氏距离相结合，提出多变量系统的Hurst控制性能指标［9］。2021年，MARYAM K和JAVAD P扩展了基于Hurst指数的多变量系统控制性能指标，给出了多变量系统性能指标的上下界［10］。蒋雄杰等将Hurst评价指标应用到火电机组控制系统性能评价上，验证了Hurst评价指标的有效性［11］。

影响一个控制回路性能优劣的因素很多，通过对控制器进行参数调整是控制性能优化的主要研究内容之一，而PID控制器在各个控制领域中应用广泛，因此笔者研究PID控制参数的整定优化，将Hurst控制性能指标引入到PID参数优化校正中，从而提高系统的控制性能。PID参数自整定由ASTROM K J等提出，以辨识过程模型参数为基础，根据被控过程特性的变化自动计算出新的控制参数［12，13］。随着计算机技术的飞速发展和人工智能技术的兴起，模糊控制、神经网络控制、遗传算法及数据驱动控制等智能算法与常规PID控制相结合，形成智能PID控制。智能PID控制器不仅具有常规PID控制器结构简单、可靠性高及鲁棒性强等特点，而且具有自学习、自适应和自组织能力。文献［14］提出了一个用线性形式模糊控制微分方程表示的模糊PID控制系统，研究此系统的性质。文献［15］开发了一种自适应傅里叶级数神经网络PID控制器结构，该控制器可以在线调整以抑制扰动效应并补偿系统参数的变化。文献［16～18］将遗传算法PID控制应用在压力罐系统控制、机器人挖掘机轨迹控制和风力发电系统控制中，验证了遗传算法PID控制具有优异的PID参数优化能力。文献［19，20］针对非线性系统分别提出了离线更新数据驱动PID控制器的数据库方法和基于自适应更新规则的数据驱动PID控制器设计方法，对非线性系统具有良好的控制性能。这些智能PID控制方法的出现使得PID控制保持着持久的生命力，继续在工业控制领域发挥重要作用。

笔者使用Hurst指数对具有随机扰动的单变量控制系统进行控制性能评价，将Hurst控制性能指标引入单变量PID控制参数校正中，提出一种基于Hurst指数的PID参数优化方法，定义结合Hurst控制性能指标、绝对误差积分和控制作用限制项的目标函数，使用遗传算法求解目标函数得到优化的PID控制参数，从而提高PID控制的控制性能，保证控制系统取得良好的控制效果。

1问题描述

考虑一个如图1所示的具有随机扰动的单变量控制过程，其中r是设定值输入，u是PID控制器输出，y是过程输出，e是系统误差，e=r-y。被控对象G（z）=z[^][G]（z），其中d为时延，[^][G]（z）是没有延迟的对象传递函数。a是一系列独立且均匀分布的白噪声序列，其均值为0、方差为σ。N（z）是扰动模型；D代表影响过程输出的扰动，由白噪声序列a通过扰动模型N（z）得到。

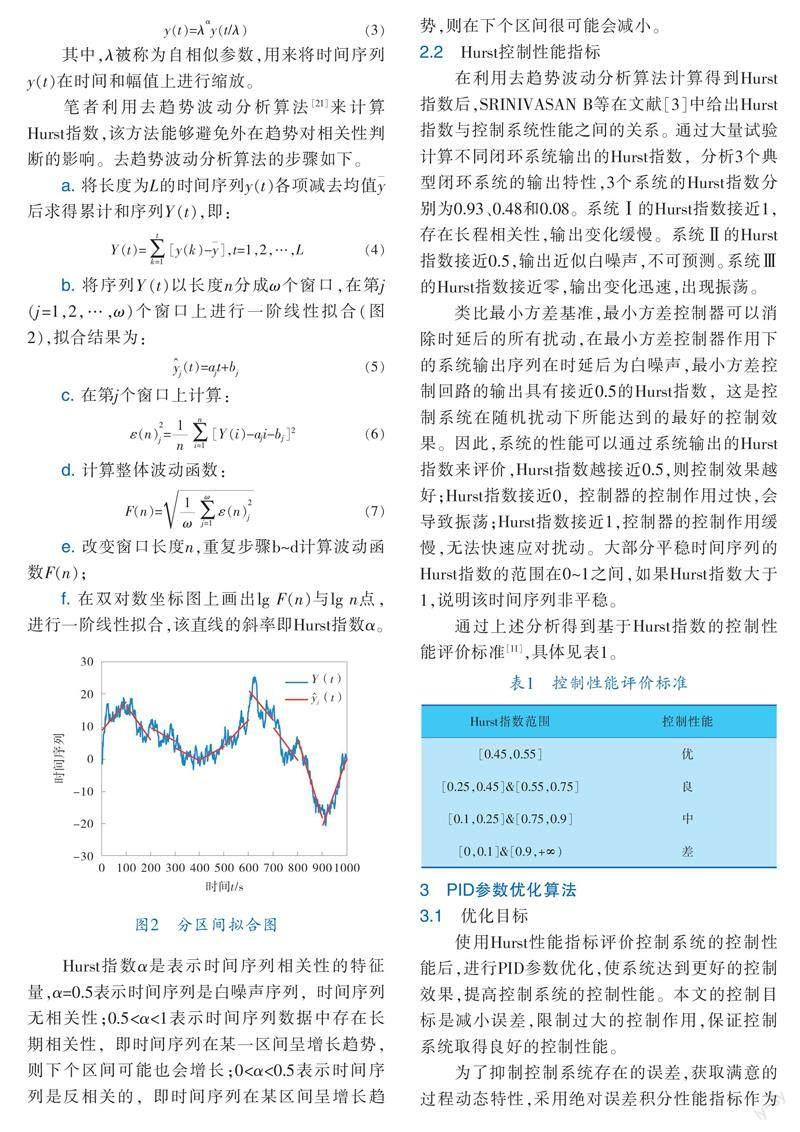
Hurst指数α是表示时间序列相关性的特征量，α=0.5表示时间序列是白噪声序列，时间序列无相关性；0.5<α<1表示时间序列数据中存在长期相关性，即时间序列在某一区间呈增长趋势，则下个区间可能也会增长；0<α<0.5表示时间序列是反相关的，即时间序列在某区间呈增长趋势，则在下个区间很可能会减小。

2.2 Hurst控制性能指标

在利用去趋势波动分析算法计算得到Hurst指数后，SRINIVASAN B等在文献［3］中给出Hurst指数与控制系统性能之间的关系。通过大量试验计算不同闭环系统输出的Hurst指数，分析3个典型闭环系统的输出特性，3个系统的Hurst指数分别为0.93、0.48和0.08。系统Ⅰ的Hurst指数接近1，存在长程相关性，输出变化缓慢。系统Ⅱ的Hurst指数接近0.5，输出近似白噪声，不可预测。系统Ⅲ的Hurst指数接近零，输出变化迅速，出现振荡。

类比最小方差基准，最小方差控制器可以消除时延后的所有扰动，在最小方差控制器作用下的系统输出序列在时延后为白噪声，最小方差控制回路的输出具有接近0.5的Hurst指数，这是控制系统在随机扰动下所能达到的最好的控制效果。因此，系统的性能可以通过系統输出的Hurst指数来评价，Hurst指数越接近0.5，则控制效果越好；Hurst指数接近0，控制器的控制作用过快，会导致振荡；Hurst指数接近1，控制器的控制作用缓慢，无法快速应对扰动。大部分平稳时间序列的Hurst指数的范围在0～1之间，如果Hurst指数大于1，说明该时间序列非平稳。

通过上述分析得到基于Hurst指数的控制性能评价标准［11］，具体见表1。

3 PID参数优化算法

3.1 优化目标

使用Hurst性能指标评价控制系统的控制性能后，进行PID参数优化，使系统达到更好的控制效果，提高控制系统的控制性能。本文的控制目标是减小误差，限制过大的控制作用，保证控制系统取得良好的控制性能。

为了抑制控制系统存在的误差，获取满意的过程动态特性，采用绝对误差积分性能指标作为参数优化的目标函数。为了防止控制能量过大，在目标函数中加入控制输入的平方项，这两个指标要求越小越好。选用下式作为控制系统的目标函数：

为了求解这样的优化问题，笔者使用遗传算法。遗传算法是HOLLAND根据自然界中适者生存的法则和基因遗传的思想提出的一种优化算法，遗传算法适用于求解复杂的优化问题，不需要初始信息就可以求得全局最优解。

笔者使用遗传算法对PID控制器参数进行优化。首先将K、K、K进行实数编码，再将3个编码串联起来组成一个整体编码。根据具体控制系统，确定3个待优化参数的搜索范围。

然后确定适应度函数。由于遗传算法针对最大化问题，而文中目标函数J越小控制效果越好，属于最小化问题，所以文中的适应度函数f采用目标函数J的倒数，f=1/J。

最后进行遗传操作，通过选择、交叉和变异产生新的更适合环境的个体。选择是从旧种群中选择生命力强的个体产生新种群。交叉是通过两个染色体的交换组合，产生新的优良品种。变异是以很小的概率随机改变遗传基因的值，避免进化过程在早期就陷入局部最优解，影响优化结果。

3.2 算法步骤

基于Hurst指数的PID控制参数优化过程如图3所示，算法步骤如下：

a. 确定遗传参数，产生初始种群。

b. 确定PID参数范围，对PID参数实数编码。

c. 使用初始PID参数得到系统输出数据，计算系统的Hurst指数与目标函数值，同时得到适应度函数值。

d. 对PID参数种群进行遗传操作（选择、交叉、变异）。计算每个PID参数个体的适应度函数值，其中适应度函数值高的个体遗传产生下一代。

e. 判断是否满足终止条件。若满足条件则停止遗传操作，不满足则继续执行步骤d直到满足终止条件。

f. 从最终的PID参数种群中选取适应度值最大的PID参数个体，将该个体反编码得到优化的PID控制参数。

4 仿真研究

4.1 数值仿真

对一个带有纯时延的二阶对象进行了仿真试验。被控对象传递函数为：

均值为0、方差为0.01的随机扰动信号a经过扰动模型叠加在系统的输出端，扰动模型为：

系统设定值输入r=33，利用经验法整定获得一组PID控制器参数K=1.15，K=0.2，K=1.8，参考这组参数确定笔者所提方法的PID参数范围。为了避免产生过大、不切实际的控制作用，将PID控制作用输出限制在［-10，10］。遗传进化100代得到优化结果，优化后PID参数K=0.2100，K=0.0073，K=0.6892，将两组PID参数作用下的控制效果进行对比。目标函数J的优化过程和Hurst指数变化过程如图4所示，两组PID参数控制作用对比如图5所示，系统输出响应曲线对比如图6所示。

由图4～6可知，经验法参数作用下的系统输出误差较大，PID控制器控制作用过大，系统Hurst指数为0.162 5，系统控制效果不太理想。经过笔者所提方法优化，目标函数J逐渐减小并趋于稳定，Hurst指数从0.162 5优化到0.454 4，处于控制性能指标的最优区间，控制性能得到了提高。系统输出动态响应速度快，输出值迅速达到设定值且输出误差小，限制了过分强烈的控制作用，控制系统取得满意的控制效果。

4.2 工业实例

笔者以某工厂脱硫浆液pH值控制回路为工业实例进行分析。脱硫浆液pH值在5.5左右时脱硫效果最好。通过采集某电厂控制系统中的实际运行数据进行辨识，脱硫浆液pH值控制系统的传递函数为：

pH设定值r=5.5，使用经验法整定得到PID控制器参数K=0.4，K=0.1，K=0.3。经过100代的遗传进化得到优化后的PID参数K=0.2478，K=0.0041，K=0.4836，将两组PID参数作用下的控制效果进行对比。目标函数J的优化过程和Hurst指数变化过程如图7所示，两组PID参数控制作用对比如图8所示，系统阶跃响应曲线对比如图9所示。

由图7～9可知，经验法参数作用下的控制系统输出误差较大，系统Hurst指数为0.152 9，系统控制效果不佳。使用笔者提出的方法进行优化，可以看到目标函数J逐渐减小，优化PID参数作用下控制系统的Hurst指数为0.504 7，处于控制性能的最优区间，系统控制性能得到了提高。系统控制作用变小，控制能量小，保证执行器的安全长久使用；系统输出稳定在设定值附近且误差小，满足脱硫浆液pH值的控制要求，能够达到较好的脱硫效果，同时满足煤炭燃烧烟气的排放要求。

5 结束语

笔者提出一种基于Hurst指数的PID参数优化方法，使用遗传算法来求解这个优化问题。研究结果表明，笔者所提方法能够有效增强PID控制器参数的优化效果，提高PID控制系统的控制性能。在后续工作中将进一步研究目标函数的定义、权重系数的选择，研究使用其他优化算法求解目标函数，以提高控制系统的性能。该方法是针对单变量系统的，将研究扩展到多变量系统将是今后要开展的工作方向之一。

参 考 文 献

［1］   ENDER D B.Process control performance： Not as good as you think［J］.Control Engineering Practice，1993，40（10）：180-190.

［2］   HURST H E.Long?term storage capacity of reservoirs［J］.Trans Amer Soc Civ Eng，1951，116：770-799.

［3］ SRINIVASAN B，SPINNER T，RENGASWAMY R.Control loop performance assessment using detrended fluctuation analysis （DFA）［J］.Automatica，2012，48（7）：1359-1363.

［4］   HARRIS T J.Assessment of control loop performance［J］.The Canadian Journal of Chemical Engineering，1989，67（5）：856-861.

［5］   HUANG B，SHAH S L，KWOK E K. Good，bad or optimal Performance assessment of multivariable processes［J］.Automatica，1997，33（6）：l175-1l83.

［6］   GRIMBLE M J.Controller performance benchmarking and tuning using generalized minimum variance control［J］.Automatica，2002，38（12）：2111-2119.

［7］   HUANG B. A pragmatic approach towards assessment of control loop performance［J］.International Journal of Adaptive Control and Signal Processing，2003，17（7?9）：589-608.

［8］   PILLAY N，GOVENDER P.A data driven approach to performance assessment of PID controllers for setpoint tracking［J］.Procedia Engineering，2014，69：1130-1137.

［9］   DAS L，SRINIVASAN B，RENGASWAMY R.Multivar?

iate Control Loop Performance Assessment with Hurst Exponent and Mahalanobis Distance［J］.IEEE Transa?

ctions on Control Systems Technology，2016，24（3）：1067-1074.

［10］   MARYAM K，JAVAD P.Data?driven performance assessment of multivariable control loops using a modified Hurst exponent?based index［J］.Proceedings of the Institution of Mechanical Engineers Part Ⅰ?Journal of Systems and Control Engineering，2021，235（6）：769-780.

［11］   蒋雄杰，罗雨颋，王印松，等.基于Hurst指数的火电机组控制系统性能评价方法［J］.控制工程，2021，28（9）：1850-1855.

［12］   ASTROM K J，HAGGLUND T.Automatic tuning of PID controllers［M］.North Carolina：Instrument Society of America，1988.

［13］  ASTROM K J，HAGGLUND T，HANG C C，et al.Automatic tuning and adaptation for PID controllers?A survey［J］.Control Engineering Practice，1993，1（4）：699-714.

［14］   PHU N D，HUNG N N，AHMADIAN A，et al.A New Fuzzy PID Control System Based on Fuzzy PID Controller and Fuzzy Control Process［J］.International Journal of Fuzzy Systems，2020，22（7）：2163-2187.

［15］  BENRABAH M，KARA K，AITSAHED O，et al.Adaptive Fourier Series Neural Network PID Contr?

oller［J］.International Journal of Control Automation and Systems，2021，19（10）：3388-3399.

［16］   UNAL M，ERDAL H，TOPUZ V.Trajectory tracking performance comparison between genetic algorithm and ant colony optimization for PID controller tuning on pressure process［J］.Computer Applications in Engineering Education，2012，20（3）：518-528.

［17］  FENG H，YIN C B，WENG W W，et al.Robotic excavator trajectory control using an improved GA based PID controller［J］.Mechanical Systems and Signal Processing，2018，105：153-168.

［18］   LI J S，LI W G.On?Line PID Parameters Optimization Control for Wind Power Generation System Based on Genetic Algorithm［J］.IEEE Access，2020，8：137094-137100.

［19］   WAKITANI S，YAMAMOTO T，GOPALUNI B.Design and Application of a Database?Driven PID Controller with Data?Driven Updating Algorithm［J］.Industrial & Engineering Chemistry Research，2019，58（26）：11419-11429.

［20］   YU H，GUAN Z，CHEN T W，et al.Design of data?driven PID controllers with adaptive updating rules［J］.Automatica， 2020，121：109185.

［21］   PENG C K，BULDYREV S V，GOLDBERGER A L，et al.Long range correlation in nucleotide sequences［J］.Letters to Nature，1992，356：168-170.

（收稿日期：2022-07-31，修回日期：2023-03-14）

PID Parameters Optimization Based on Hurst Index

SHAN Gang?sheng， WANG Zhi?guo， LIU Fei

（Key Laboratory for Advanced Process Control of Light Industry of the Ministry of Education，Jiangnan University）

Abstract   For purpose of improving the control performance of PID control process， a PID parameter optimization method based on Hurst index was proposed. Firstly， a control performance evaluation method based on the Hurst index was presented； then， through based on the Hurst control performance index and combined with the absolute error integral and the controllers output limitation， the objective function of PID parameter optimization was defined and PID parameters were obtained by using the genetic algorithm. Numerical simulation and industrial cases verify effectiveness of the method proposed.

Key words   PID parameter optimization， Hurst index， control performance assessment， genetic algorithm

作者簡介：单港生（1997-），硕士研究生，从事控制系统性能评价与优化等的研究。

通讯作者：王志国（1977-），副教授，从事工业过程控制性能评价和优化方面的教学与科研工作，zhiguowang@jiangnan.edu.cn。

引用本文：单港生，王志国，刘飞.基于Hurst指数的PID控制参数优化［J］.化工自动化及仪表，50（2）：158-164.