基于自适应拟合的智能车换道避障轨迹规划*
李 军,周 伟,唐 爽
(1.重庆交通大学机电与车辆工程学院,重庆 400074;2.轨道交通车辆系统集成与控制重庆市重点实验室,重庆 400074)
前言
换道避障轨迹规划是自动驾驶车辆领域的关键技术之一[1],稳定的换道避障行为能够提高车辆通行效率。换道避障轨迹规划需要在安全避开障碍物的前提下规划一条连续且光滑的换道轨迹[2]。目前常用的避障轨迹规划方法可以分为基于参数化曲线的算法[3]、基于网格的搜索算法[4]、基于采样的规划方法[5]、人工势场算法[6]和基于离散化规划的算法[7-9]5类。基于参数化曲线算法的轨迹规划方法由于路径曲线形状的限制存在不易实现实时避障的缺点。基于网格的启发式搜索轨迹规划方法在进行较大区域轨迹规划时存在计算量较大的问题。基于采样的轨迹规划方法由于采样随机的原因存在计算量较大和路径不够平滑的缺点。基于人工势场算法的轨迹规划方法由于没有考虑车辆运动学约束的原因存在所规划的轨迹不可行的可能。基于离散化优化的轨迹规划方法对车辆行驶道路进行有序的采样,不存在难以避障、计算量大、盲目性大和所规划的轨迹不可行的缺点。
模型预测控制算法的优点是可以在控制过程中添加多种约束[10-16],因此,模型预测控制算法被广泛用于自动驾驶车辆[17-27]、机器人和无人机等领域的轨迹规划。Hu 等[22]基于模型预测控制算法搭建了车辆轨迹规划和跟踪的集成框架,能够成功完成静态和动态障碍物的规避。Wang 等[23]基于模型预测控制算法设计了适合点障碍物的轨迹规划方法,在动态避障环境中取得了较好的效果。Gao 等[24]搭建了模型避障预测轨迹规划的框架,实现了不同速度工况下的避障轨迹规划,但轨迹规划控制器未考虑轨迹的曲率问题。Liu 等[25]基于模型预测控制设计了高速工况下的轨迹规划方案,在静态避障环境下获得了良好效果,但没有考察动态避障环境。Li等[26]结合人工势场理论,综合考虑车辆状态信息和障碍物的相对位置及速度信息,建立了惩罚函数,引入了优化目标函数,基于模型预测算法设计了避障轨迹规划的方案,实现了车辆的静态和动态避障轨迹规划,但未考虑到障碍物与车辆的相对最小距离。Park 等[27]考虑车辆与障碍物的视差角设计避障函数,基于模型预测算法设计避障轨迹规划方案,实现了不同速度工况下的车辆避障轨迹规划,但没有考虑到速度对避障轨迹规划的影响。
针对以上问题,本文定义坐标系和动态换道避障场景,搭建被控车辆和障碍车辆模型,确定车辆换道避障轨迹规划的行驶约束条件,考虑模型预测控制轨迹规划算法提供的不包含曲率信息的一系列离散点可能生成不可行轨迹的问题,设计一种基于五次贝塞尔曲线并考虑曲率信息的自适应轨迹拼接拟合方法,进一步基于模型预测控制算法设计自动驾驶车辆换道避障轨迹规划方法。
总之,本文提供了一种面向动态环境的自动驾驶车辆换道避障轨迹规划方法,所提出的方法基于五次贝塞尔曲线自适应分段拟合换道避障轨迹规划的离散点序列,拟合轨迹包含曲率信息。所提出的方法基于模型预测控制算法进行轨迹规划,该方法考虑障碍车辆模型。因此,该方法可用于高速动态避障环境。
1 动态换道避障场景
1.1 定义坐标系及换道避障场景
为描述车辆的运动定义两个坐标系:惯性坐标系XOY和车身坐标系xoy。当前车辆在直道进行换道避障,被控车辆行驶车道中心线前方和目标车道中心线上对应存在以一定速度行驶的障碍车辆,如图1所示。
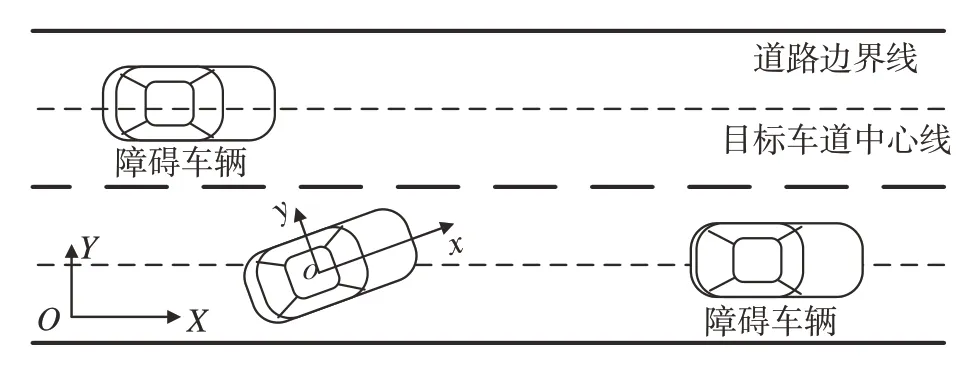
图1 坐标系及换道避障场景
1.2 换道避障轨迹规划车辆行驶条件
避障轨迹规划的需要在满足车辆行驶条件下最小化参考轨迹与规划轨迹之间的偏差,车辆行驶条件如下:
式中:vmin、v和vmax分别为允许最小车速、车速和允许最大车速;Rmin、R分别为车辆允许最小转弯半径、车辆转弯半径;amin和amax分别为车辆最小横向加速度和车辆最大横向加速度;b1和b2分别为两条道路边界线的横向坐标;Ym为规划轨迹的横向坐标;μ为路面附着系数;g为重力加速度;W为车辆宽度。
1.3 被控车辆和障碍物车辆模型
对于动态避障环境,需要搭建被控车辆和障碍车辆模型,换道避障轨迹规划采用忽略车身尺寸和轮胎受力情况的刚体运动学模型,该模型可以表示如下[2]:
式中:ax和ay分别为车身坐标系下车辆纵向加速度和横向加速度;ψ和φ分别为车辆横摆角和航向角;分别是车辆在惯性坐标系中的纵向速度和横向速度。
2 自适应轨迹拟合算法
2.1 五次贝塞尔曲线表达形式
基于五次贝塞尔曲线的自适应轨迹拟合算法被设计用以拟合轨迹规划的离散点序列。
贝塞尔曲线[2]可以表示为
式中:q(τi)为在参数τi处的插值点;m为贝塞尔曲线的阶次;Pk为贝塞尔曲线的控制点。
设P0、P1、P2、P3、P4、P5为贝塞尔曲线的控制点,五次贝塞尔曲线可以表示为
转变为矩阵的形式可以表示为
贝塞尔曲线在任一点的曲率k可以表示为
由于贝塞尔曲线是被用于离散点序列的拟合,根据离散点的坐标贝塞尔曲线的曲率可以表示为
2.2 轨迹拼接辅助点设计
在每两段相邻曲线处补充设计一个辅助控制点Q1,贝塞尔曲线拼接示意图如图2 所示。最优辅助控制点Q1满足条件如下:
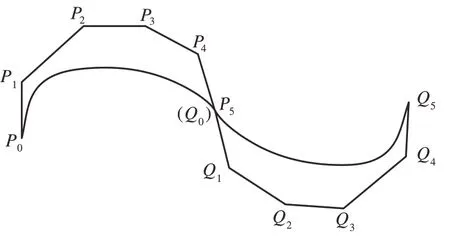
图2 贝塞尔曲线拼接示意图
式中Q0、Q2和Q3分别是下一段拼接轨迹上除辅助控制点以外的前3个控制点。
其中,式(8)表示最小化线段P5-P4、线段P4-P3、线段P3-P2、线段Q2-Q1和线段Q1-Q0代数和的长度。式(9)分别表示Q1处于Q0(P5)与Q2中间的合适位置;线段Q1-Q0的长度小于线段Q2-Q1的长度;线段P5-P4和线段Q1-Q0共线;P5=Q0表示第1 段末尾点与第2段第1个点重合。
2.3 轨迹自适应拟合流程
可以得到1 阶贝塞尔曲线的控制点坐标,表示如下:
式中:p1,1、p1,2、p1,3、p1,4、p1,5为贝塞尔曲线的1 阶控制点坐标;p0、p1、p2、p3、p4、p5为贝塞尔曲线的控制点坐标。
可以得到2 阶贝塞尔曲线的控制点坐标,表示如下:
式中p2,1、p2,2、p2,3、p2,4为贝塞尔曲线的2 阶控制点坐标。
可以得到3阶贝塞尔曲线的控制点,表示如下:
式中p3,1、p3,2、p3,3为贝塞尔曲线的3阶控制点坐标。
可以得到4 阶贝塞尔曲线的控制点坐标,表示如下:
式中p4,1、p4,2为贝塞尔曲线的4阶控制点坐标。
可以得到5 阶贝塞尔曲线的控制点坐标,表示如下:
式中p5,1为贝塞尔曲线的5阶控制点坐标。
拟合残差的平方和可以表示为
基于五次贝塞尔曲线的轨迹规划的离散点序列拟合流程如图3所示。

图3 轨迹自适应拟合流程
3 车辆换道避障模型预测轨迹规划
3.1 车辆避障函数
考虑到车速的影响以及惩罚函数在避障目标函数中所占的比例,避障函数[26]由下式给出:
式中:Jobs,i为避障函数;Sobs为避障权重;dmin为车辆距离障碍物的最小距离;ζ是一个极小的正数,用于避免分母为零。
3.2 离散化控制模型
3.2.1 状态变量选取
3.2.2 线性化控制模型
式(17)是连续非线性方程,需要将该方程进行线性化和离散化。
采用泰勒展开,式(17)可以转变为
式中:X0和u0为状态方程当前时刻的输入;J(X)和J(u)为雅可比矩阵。
式(18)可以转变为线性化状态方程:
3.2.3 离散化控制模型
对式(19)进行离散化处理,则式(19)转变如下:
模型预测控制系统预测输出与当前状态的关系为
其中,避障轨迹规划控制器的横向位移输出矩阵为
避障轨迹规划控制器的状态矩阵表示如下:
避障轨迹规划控制器的控制矩阵表示如下:
3.3 车辆换道避障轨迹规划目标函数
车辆换道避障轨迹规划的控制目标是避开障碍物的条件下最小化规划轨迹与参考轨迹的偏差,车辆换道避障轨迹规划目标函数可以表示为
式中:Q和R为权重矩阵;η和ηref分别为避障轨迹规划控制器的预测轨迹和参考轨迹;umax和umin分别为控制量的最大值和最小值;△umax和△umin分别为控制增量的最大值和最小值。
3.4 车辆换道避障轨迹跟踪目标函数
轨迹跟踪车辆模型选用考虑车辆轮胎侧偏特性的2 自由度车辆动力学模型[28],换道避障轨迹跟踪控制器采用文献[2]中的模型预测标准目标函数。
3.5 车辆换道避障稳定性分析
为验证本文提出的轨迹规划方法的稳定性,利用横摆角速度约束方程式(27)和质心侧偏角约束方程式(28)形成闭合包络,如图4所示[28]。

图4 稳定性约束包络示意图
车辆横摆角速度的控制边界可以表示如下:
式中:r是车辆的横摆角速度;vx是车辆的纵向速度。
车辆质心侧偏角的控制边界可以表示如下:
式中:β为车辆的质心侧偏角;Cαr为后轮等效侧偏刚度;a和b分别为从车辆质心到前轴和后轴的距离。
4 动态避障仿真结果与分析
4.1 动态避障方案设定
为验证本文车辆换道避障轨迹规划方案的有效性,按照A、B 两种方案进行车辆动态换道避障轨迹规划仿真分析。仿真车辆模型的基本参数如表1所示。

表1 车辆模型基本参数
A.障碍车辆1 和障碍车辆2 以初始时刻的运动状态匀速行驶。
B.障碍车辆1 以1 m/s2加速度加速到指定速度后以指定速度匀速行驶;障碍车辆2 以初始时刻的运动状态匀速行驶。
4.2 动态环境换道避障轨迹规划验证
同时,为验证本文中提出的自适应拟合算法的拟合轨迹的有效性,将自适应拟合算法的拟合轨迹与多项式拟合轨迹进行仿真对比分析。
车辆以方案A 在不同速度工况下换道避障轨迹规划结果如图5所示。在图5(a)中,障碍车辆1和障碍车辆2 在图示位置以56 km/h 的速度匀速行驶,自车以70 km/h的初速度在图示位置行驶,定义为工况1。从图5(a)可以看出,本文的换道避障轨迹规划方案在工况1 能够完成障碍物的规避。在图5(b)中,障碍车辆1和障碍车辆2在图示位置以64 km/h的速度匀速行驶,自车以80 km/h的初速度在图示位置行驶,定义为工况2。从图5(b)可以看出,本文的换道避障轨迹规划方法在工况2 能够完成障碍物的规避。在图7(c)中,障碍车辆1和障碍车辆2在图示位置以72 km/h 的速度匀速行驶,自车以90 km/h 的初速度在图示位置行驶,定义为工况3。从图5(c)可以看出,本文的换道避障轨迹规划方案能够在工况3完成障碍物的规避。
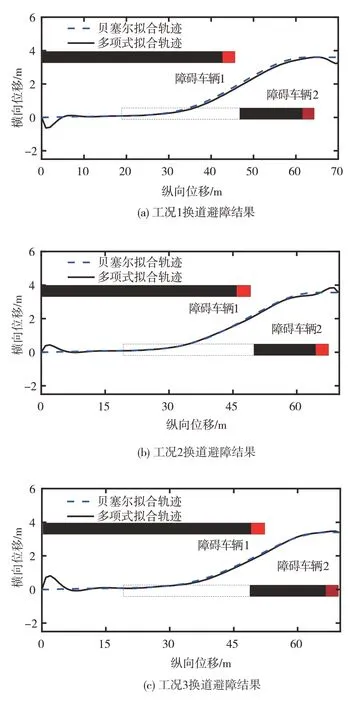
图5 方案A在不同工况下换道避障轨迹规划结果
同时,从图5 可以看出,多项式拟合在拟合较多的离散点时,为逼近所有的点,会在拟合开始和结束时产生震荡现象,由于贝塞尔曲线的凸包特性,本文提出的自适应拟合算法的拟合轨迹与多项式拟合轨迹相比更平滑。
车辆以方案B 在不同速度工况下换道避障轨迹规划结果如图6 所示。在图6(a)中,障碍车辆1 以1 m/s2加速度在图示位置以56 km/h的初速度加速至70 km/h,障碍车辆2在图示位置以56 km/h的速度匀速行驶,自车以70 km/h 的初速度在图示位置行驶,定义为工况1。从图6(a)可以看出,本文的换道避障轨迹规划方法在工况1 能够完成障碍物的规避。在图6(b)中,障碍车辆1以1 m/s2加速度在图示位置以64 km/h 的初速度加速至80 km/h,障碍车辆2 在图示位置以64 km/h的速度匀速行驶,自车以80 km/h 的初速度在图示位置行驶,定义为工况2。从图6(b)可以看出,本文的换道避障轨迹规划方法在工况2 能够完成障碍物的规避。在图6(c)中,障碍车辆1以1 m/s2加速度在图示位置以72 km/h的初速度加速至90 km/h,障碍车辆2 在图示位置以72 km/h 的速度匀速行驶,自车以90 km/h的初速度在图示位置行驶定义为工况3。从图6(c)可以看出,本文的换道避障轨迹规划方法能够在工况3 完成障碍物的规避。

图6 方案B不同工况下换道避障轨迹规划结果
从图6 可以看出,在拟合较多的离散点时,本文提出的自适应拟合算法的拟合轨迹相比于多项式拟合轨迹更平滑。
4.3 自适应拟合算法拟合残差
车辆以方案A 在不同工况下换道避障轨迹规划提供的离散点序列与贝塞尔曲线对应点的拟合残差如图7 所示。从图7 可以看出,车辆以方案A 在不同工况下换道避障轨迹规划提供的离散点序列与贝塞尔曲线对应点的拟合残差都保持在拟合阈值以内。
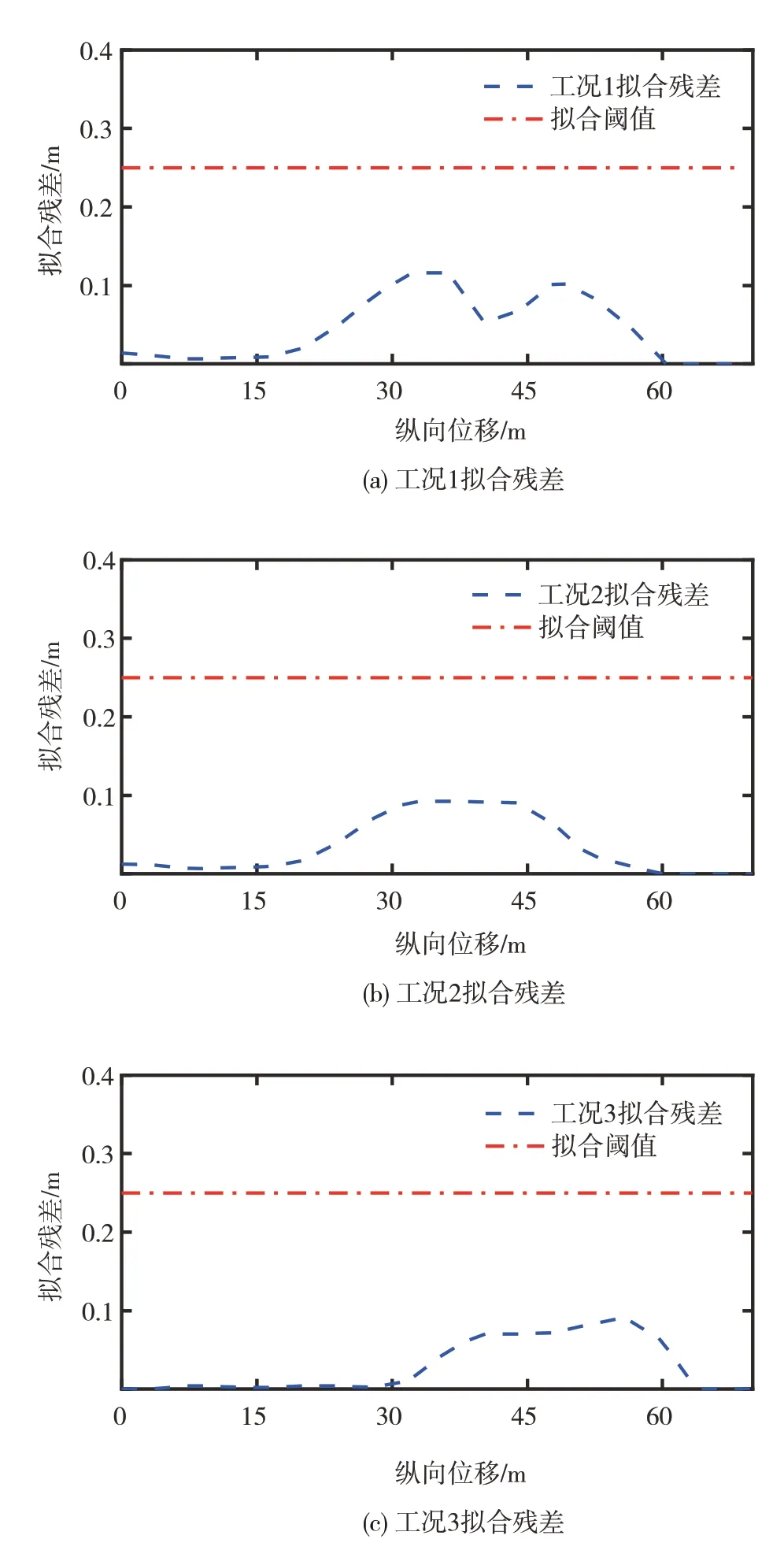
图7 方案A在不同工况下换道避障轨迹拟合残差
车辆以方案B 在不同工况下换道避障轨迹规划提供的离散点序列与贝塞尔曲线对应点的拟合残差如图8 所示。从图8 可以看出,车辆以方案B在不同工况下换道避障轨迹规划提供的离散点序列与贝塞尔曲线对应点的拟合残差都保持在拟合阈值以内。

图8 方案B在不同工况下换道避障轨迹拟合残差
4.4 被控车辆动力学参数分析
车辆以方案A 在不同速度工况下换道避障轨迹规划相关动力学参数曲线如图9所示。由图9可知,被控车辆的前轮转角、横向加速度和轮胎侧偏角都处于执行机构的机械饱和约束范围内。
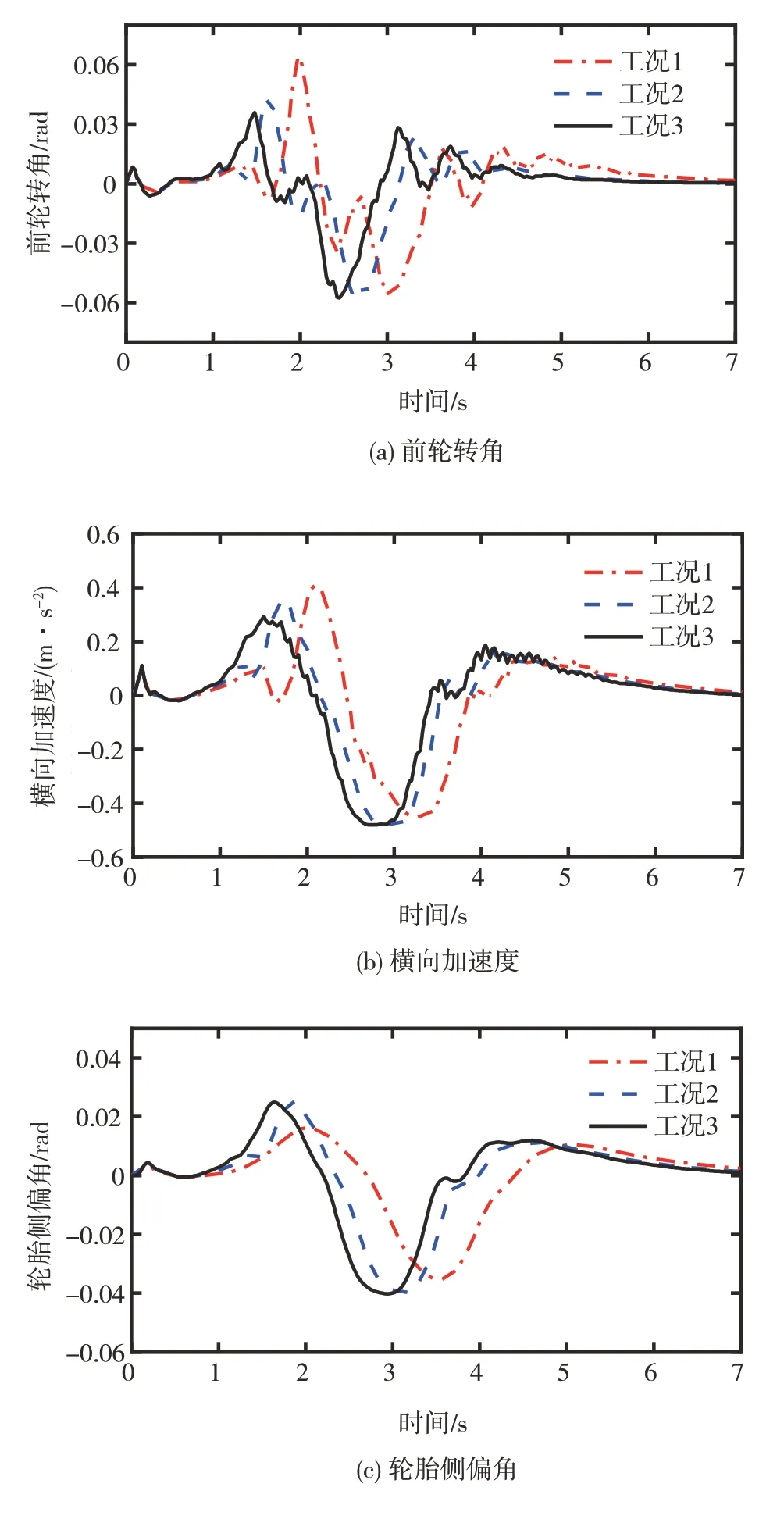
图9 方案A 在不同工况下换道避障轨迹规划的前轮转角、横向加速度和轮胎侧偏角
车辆以方案B 在不同工况下换道避障轨迹规划相关动力学参数曲线如图10所示。由图10可知,被控车辆的前轮转角、横向加速度和轮胎侧偏角都处于执行机构的机械饱和约束范围内。
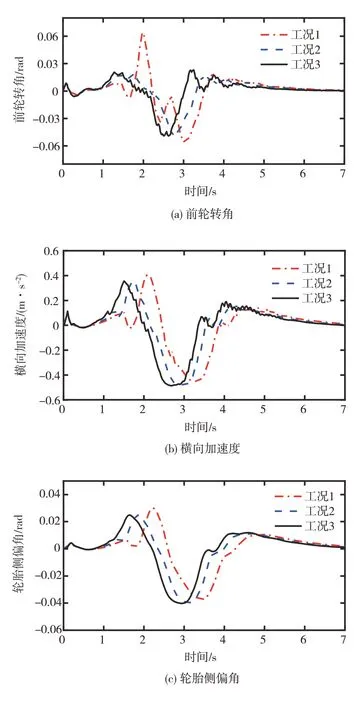
图10 方案B 在不同工况下换道避障轨迹规划的前轮转角、横向加速度和轮胎侧偏角
4.5 换道避障轨迹规划方法稳定性分析
车辆以方案A 在不同速度工况下换道避障轨迹规划稳定性验证结果如图11 所示。由图11 可知,车辆的横摆角速度和质心侧偏角一直处于包络之内,说明被控车辆在不同工况下都处于稳定状态。
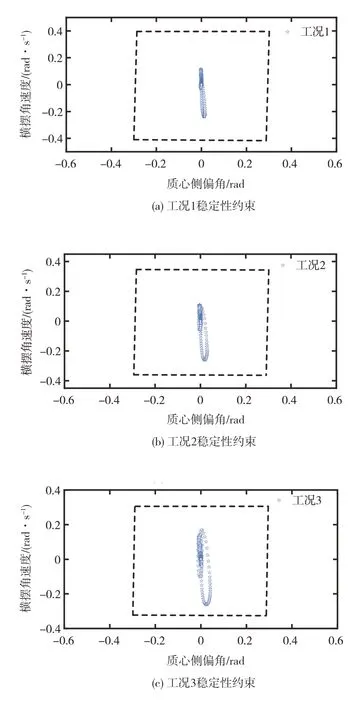
图11 方案A在不同工况下的稳定性约束验证
车辆以方案B 在不同速度工况下换道避障轨迹规划稳定性验证结果如图12所示。由图12可知,车辆的横摆角速度和质心侧偏角一直处于包络之内,说明被控车辆处于稳定状态。

图12 方案B在不同工况下的稳定性约束验证
5 结论
(1)定义了动态换道避障轨迹规划环境,进而确定车辆换道避障轨迹规划的行驶约束条件,搭建了轨迹规划被控车辆和障碍车辆模型。
(2)设计了基于五次贝塞尔曲线的自适应分段拟合算法拟合换道避障轨迹规划的离散点序列,拟合轨迹连续且光滑,换道避障轨迹规划提供的离散点序列与贝塞尔曲线对应点的拟合残差都保持在拟合阈值内。
(3)基于模型预测控制算法设计了换道避障轨迹规划方法。仿真结果验证了本文中提出的自动驾驶车辆换道避障模型预测轨迹规划方法在动态环境下的有效性和稳定性。
后续可研究雷达和视觉系统等信息设备与避障轨迹规划控制的集成框架,并对研究进行实车验证。

