栏杆高度对流线型箱梁涡振性能影响的试验研究
刘庆宽 ,王仰雪 ,孙一飞 ,李震 ,韩原 ,靖洪淼 ,2,†
[1.河北省风工程和风能利用工程技术创新中心(石家庄铁道大学),河北 石家庄 050043;2.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;3.石家庄铁道大学 土木工程学院,河北 石家庄 050043]
强风作用下大跨度桥梁的风致振动问题一直广受关注,其中涡激振动是大跨度桥梁在低风速时易发生的风致振动现象.当气流绕过主梁表面产生的旋涡脱落频率与主梁自振频率相同或相近时,会发生涡激共振现象.涡振的主要危害是影响行车舒适度和行车安全,持续的涡激振动还会带来桥梁结构的疲劳破坏.2020年虎门大桥发生涡激振动事件[1],进一步引起了研究者对桥梁涡激振动问题的关注.
为了达到较好的抗风性能,流线型钢箱梁被广泛地应用于目前的大跨度桥梁建设中,最近研究发现,扁平流线型箱梁也会发生涡激振动问题[2].因此,针对这类常用的大跨度桥梁断面形式,探索诱发涡激振动的原因,研发必要的振动控制措施,具有十分重要的工程意义.
大跨度桥梁风致振动的控制措施主要分为三大类:结构措施、机械措施和气动措施.对涡激振动的控制经常采用机械措施和气动措施.机械措施是在桥梁结构上添加阻尼器和控制器等[3]来改变结构的固有特性.气动措施是通过改变主梁的气动外形,进而改变气流绕流时分离和旋涡的形成,达到抑制涡振的目的.
常见抑制涡振的气动措施主要分为两类:其一是在主梁原有结构上增设附加构件,如抑流板、导流板、稳定板和风嘴等,相关研究有:杨詠昕等[4]、贺耀北等[5]和张志田等[6]提出了抑流板、导流板、稳定板等多种控制措施的选择方法;李春光等[7]、周志勇等[8]和李志国等[9]研究发现越尖锐的风嘴,改善主梁的涡振性能的效果越明显;Larsen 等[10]、许福友等[11]、郭增伟等[12]和胡传新等[13-14]通过对主梁表面气动特性的分析,揭示了抑流板和导流板的抑振机理.其二是对主梁原有附属构件进行优化设计,如人行道栏杆、防撞护栏和检修车轨道的截面尺寸、外形和位置等,相关研究有:钱国伟等[15]、朱思宇等[16]、王仰雪等[17‒18]、张天翼等[19]和李明水等[20]研究了栏杆分布位置、栏杆截面形状、栏杆倾斜角度以及栏杆透风率等参数对涡振性能的影响;刘小兵等[21]、张建等[22]和Laima 等[23]研究发现调整合适的检修车轨道位置和高度,可以有效地抑制主梁的涡振.此外,葛耀君等[24-25]、廖海黎等[26]、赵林等[27]和李明等[28-29]系统地总结了各类大跨度桥梁的气动抑振措施.
目前针对主梁上原有附属构件(栏杆和检修车轨道)对涡振性能影响的研究,主要有调整栏杆截面形式、栏杆透风率以及检修车轨道位置和高度等,但是关于栏杆高度对主梁涡振性能的影响研究较少,也缺乏相关机理的解释.因此,本文通过节段模型风洞动态测压与测振试验,研究了栏杆高度对主梁表面压力分布和主梁竖弯涡振的影响,寻找对流线型箱梁涡振性能影响最大和最小的栏杆高度,得到最优的栏杆高度取值,并揭示其对涡振的影响机理,为工程设计提供依据和参考.
1 风洞试验概况
1.1 主梁节段模型参数及模型设计
选取主梁为典型流线型断面的宁波象山港大桥为研究对象,其跨径为82 m+262 m+688 m+262 m+82 m=1 376 m,宽高比为9.71∶1,风嘴角度为56°.综合考虑风洞试验段截面尺寸、模型质量、阻塞率等要求[30],选定节段模型缩尺比为1∶30,模型长L=2 140 mm,宽B=1 070 mm,高H=117 mm,主梁节段模型断面图如图1所示.

图1 主梁节段模型断面图(单位:mm)Fig.1 Geometrical sizes of a bridge sectional model(unit:mm)
试验在石家庄铁道大学STU-1风洞实验室低速试验段内进行,该试验段高3.0 m,长24.0 m,宽4.4 m,流场背景湍流度小于0.4%.在试验段搭建弹性悬挂系统(见图2),系统主要由刚性支撑、花篮螺栓、弹簧、刚臂和主梁节段模型等组成,可实现模型的竖向和扭转振动.模型两端安装长、宽分别为主梁宽1.5倍、主梁高3.5 倍的端板,确保模型端部气流有较好的二维流动性并消除模型的端部效应[31-33].不同风攻角(α)下模型在风洞中阻塞度分别为3.42%(α=0°)、3.60%(α=±3°)和3.70%(α=±5°),阻塞度均满足小于5%的要求[34].

图2 弹性悬挂系统安装图Fig.2 Installation diagram of elastic suspension system
《公路桥梁抗风设计规范》(JTG/T 3360‒01―2018)[35]建议钢箱梁的阻尼比取0.3%,而实际中阻尼比会小于规范建议值,因此试验中模型的阻尼比也小于规范建议值,以使试验结果同实际结果更加接近.风洞试验主要参数[36]见表1.
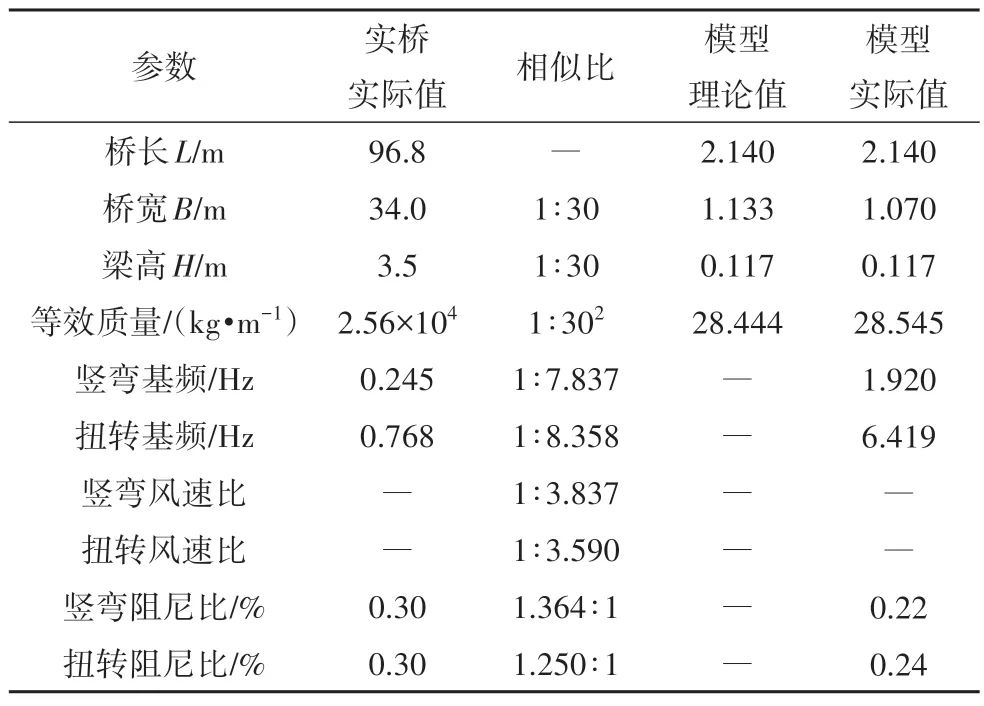
表1 风洞试验主要参数Tab.1 Main parameters of wind tunnel test
在模型的跨中位置处布置一圈测压孔,在风压可能变化敏感的部位加密布置,共180 个测压点,如图3 所示.为便于表示每个测点的坐标,定义无量纲间距Dd=d/D,d为测压点到A 点沿模型表面的累积距离,D为模型A、B 两点之间的沿模型表面累积距离.同时,为了在分析中准确定位,将主梁模型表面划分了7 个区域,见图3 中标注①~⑦.M 点和N 点是在下文频域分析时选用的代表测点.

图3 测点无量纲间距示意图Fig.3 Diagram of measuring points dimensionless distances
每根测压管长度一致,以避免测压管路长度对试验结果的影响.对比试验发现,将扫描阀放置在模型外部时,会因测压管路晃动对阻尼产生影响,因此,正式试验时将扫描阀放置在模型内部并进行固定,避免了扫描阀和测压管路对试验的影响.
1.2 试验工况
测压和测振试验在均匀流场中进行,试验风速范围为0~10 m/s,风攻角为0°、±3°、±5°.在主梁桥面防撞护栏和中央隔离栏杆保持不变的前提下,仅改变桥面外侧人行道栏杆高度,研究该处栏杆高度变化对主梁涡振性能的影响.各工况的栏杆截面形式和透风率相同.防撞护栏和中央隔离栏杆外形尺寸一致,高均为50 mm(对应实桥1.50 m),无量纲高度为0.43H,H为主梁节段模型的梁高,如图4(a)所示.

图4 栏杆示意图(单位:mm)Fig.4 Schematic diagrams of railings(unit:mm)
《城市桥梁设计规范》(CJJ 11―2011)规定[37]:人行道或安全带临空侧的栏杆高度不应小于1.10 m,非机动车道临空侧栏杆高度不应小于1.40 m,可见临空侧栏杆高度有较大的取值范围.本研究中栏杆的实际高度范围是1.23~1.95 m,在规范的取值范围之内.栏杆模型高度分别为h=41 mm(对应实桥1.23 m)、53 mm(对应实桥1.59 m)和65 mm(对应实桥1.95 m),对其高度进行无量纲化表示为h=0.35H、0.45H和0.56H,其示意图如图4(b)所示.对于桥面无任何栏杆状态工况,用h=0表示.
2 栏杆高度对主梁涡振的影响
2.1 各工况下主梁涡激振动响应
首先分析涡激振动(简称涡振)的振幅随风速的变化情况.为了研究对比方便,风速和振幅分别采用折减风速[U/(fB),其中U为来流风速,f为竖弯自振频率]和无量纲振幅(Y/H,其中Y为竖向振幅).图5所示为主梁节段模型各工况下的竖弯涡振响应随风速的变化曲线.
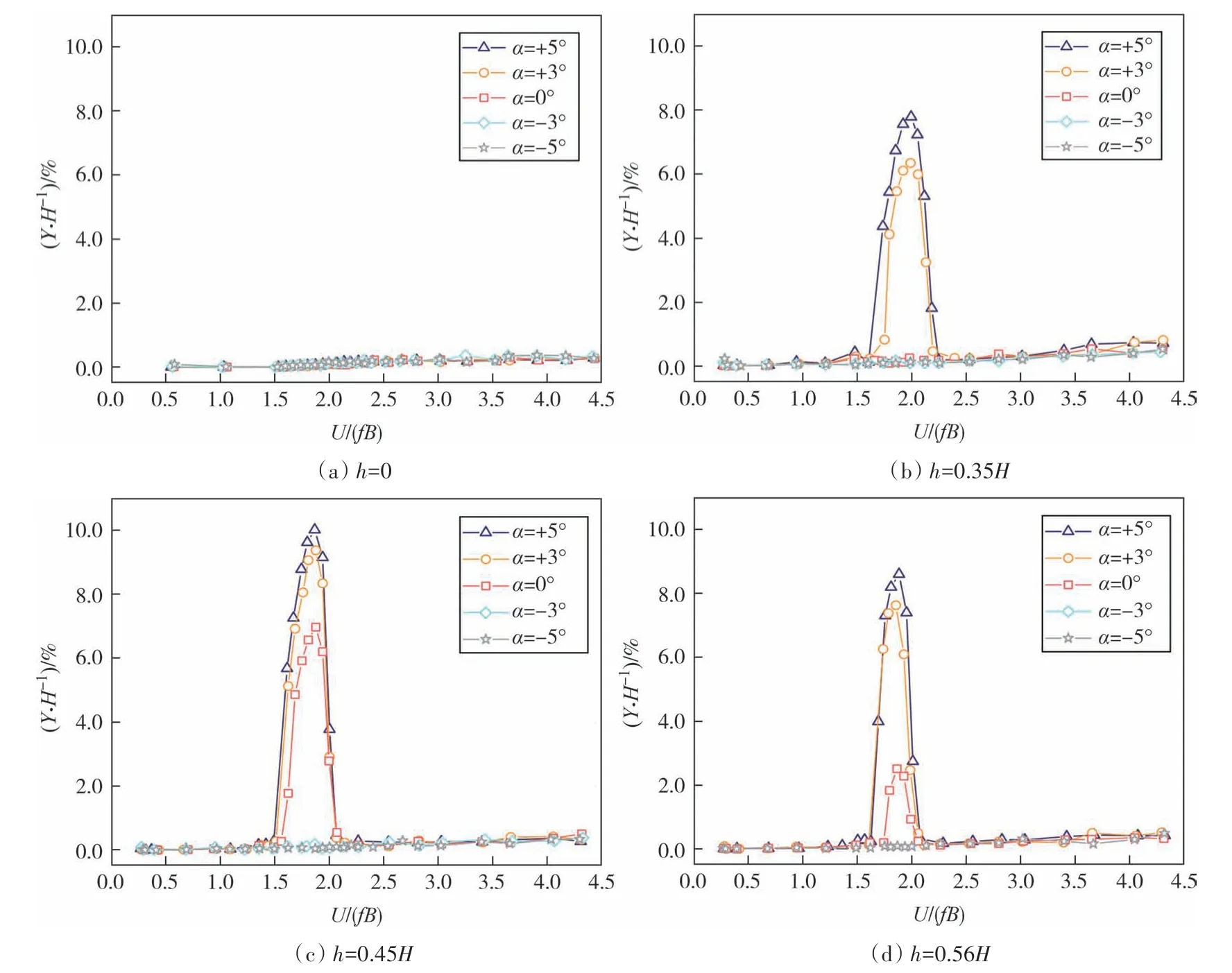
图5 不同栏杆高度、不同风攻角下主梁竖弯涡振响应Fig.5 Vertical VIV responses of main beam at different railing heights and attack angles
由图5 可知,无栏杆状态的主梁节段模型在各风攻角下均未发生涡振现象,而当桥面有栏杆存在时,部分风攻角下主梁发生了涡振现象.具体地,在α=+5°和+3°时,有栏杆的主梁均发生了涡振现象;在α=0°时,栏杆高0.35H的主梁断面未发生涡振现象,而栏杆高0.45H和0.56H的主梁发生了涡振现象;在α=-3°和 -5°时,不论主梁断面是否存在栏杆,均不发生涡振现象.由此可见,栏杆的存在会降低主梁的涡振性能,栏杆高度的变化会影响主梁涡振振幅.
2.2 栏杆高度对主梁涡振振幅的影响
由图5(b)(c)(d)可知,相同栏杆在不同风攻角下,发生涡振的风速锁定区间稍有变化.具体来说,栏杆高0.35H时,风速锁定区间U/(fB)=1.597~2.249;栏杆高0.45H时,风速锁定区间U/(fB)=1.489~2.137;栏杆高0.56H时,风速锁定区间U/(fB)=1.616~2.117.
为了分析栏杆高度的变化对主梁的涡振振幅的影响,在表2 中汇总了三种栏杆高度在α=0°、+3°和+5°时,竖弯涡振幅值最大时对应的风速和振幅.

表2 各工况涡振响应最大时的风速和振幅Tab.2 Wind speed and amplitude at maximum of VIV responses for each condition
由表2 可知,有栏杆状态下,栏杆高0.45H时主梁的涡振幅值最大,栏杆高0.35H时的涡振幅值最小,且涡振幅值大的工况锁定风速小.在不同风攻角下,栏杆高0.35H时均能够有效地抑制涡振响应,具体表现在α=+3°和+5°时,分别比栏杆高0.45H时的涡振幅值降低了32.56%和22.46%,锁定风速分别增大了0.117 和0.122,且在α=0°时可以完全抑制涡振.
3 栏杆高度对主梁涡振的影响机理
主梁表面的风压分布可以反映空气在主梁周边的绕流情况,因此对模型表面平均和脉动风压系数、风压频域特性及局部升力同涡振的贡献系数的关系进行研究,揭示栏杆高度变化对涡振的影响及作用机理.选用振幅最大时[对应U/(fB)=1.874],各工况风攻角为α=0°和+5°的风压数据结果进行分析.
3.1 平均风压系数分布
通过平均风压系数的分布来分析气流在主梁表面分离和再附等情况.各测点的风压系数计算公式如式(1):
式中:Pi为第i个测点的瞬时风压值;P0为参考点静压值;ρ为空气密度.
图6 和图7 是α=0°和α=+5°时主梁上、下表面平均风压系数的结果,平均风压系数(CP,mean)是风压系数的平均值.

图6 α =0°时主梁表面平均风压系数分布Fig.6 Distribution of mean wind pressure coefficient on girder’s surface at attack angle of 0°

图7 α =+5°时主梁表面平均风压系数分布Fig.7 Distribution of mean wind pressure coefficient on girder’s surface at attack angle of+5°
通过测点表面风压系数由正变为负,来判断气流分离点的位置.由图6(a)和图7(a)上表面风压分布可知,无栏杆状态时,气流分离点在迎风侧风嘴处前缘,而有栏杆状态时,在上表面迎风侧风嘴与桥面交界处,即栏杆的存在使得分离点位置后移.无栏杆时在0.097<Dd<0.190区域平均风压变化较为剧烈,而有栏杆时平均风压变化相对平缓.
由图6(b)和图7(b)可知,有栏杆时,下表面斜腹板前半部分平均风压系数随着Dd的增大而逐渐减小,后半部分随Dd的增大而增大,而无栏杆状态的平均风压系数在斜腹板上随Dd的增大而增大.值得注意的是,有栏杆时主梁的下表面存在三个风压的极值点,在α=0°时分别在Dd=0.096、0.227、0.794 附近;在α=+5°时分别在Dd=0.070、0.227、0.794 附近.由此可见,随着风攻角的增大,下表面第一个风压极值点的位置前移.
3.2 脉动风压系数分布
图8 和图9 分别是α=0°和+5°时主梁上、下表面脉动风压系数结果,脉动风压系数(CP,rms)是风压系数的标准差.由图8 可知,栏杆高0.45H的脉动风压变化最剧烈,其次是栏杆高0.56H、栏杆高0.35H,无栏杆状态时变化最平缓,但无栏杆状态时的脉动风压数值整体上要大于栏杆高0.56H和0.35H.由图8(a)可知,栏杆高0.45H时在0.055<Dd<0.335 和0.622<Dd<0.964 区域内,脉动风压有较大的起伏,最大脉动风压数值达0.223,约是无栏杆时最大脉动风压系数的1.8 倍.由图8(b)可知,有栏杆时,脉动风压的变化在斜腹板与底板交界处会出现极大值,而无栏杆时,下表面脉动风压变化比较缓和.栏杆高0.45H时在主梁迎风侧斜腹板前缘脉动风压变化剧烈,随后变化趋于平缓.

图8 α =0°时主梁表面脉动风压系数分布Fig.8 Distribution of fluctuating wind pressure coefficient on girder’s surface at attack angle of 0°

图9 α =+5°时主梁表面脉动风压系数分布Fig.9 Distribution of fluctuating wind pressure coefficient on girder’s surface at attack angle of +5°
由图9(a)可知,无栏杆时,主梁上表面的脉动风压系数明显小于有栏杆的工况.栏杆高0.35H和0.45H的主梁上表面脉动风压在0<Dd<0.680 和0.895<Dd<1 区域脉动风压系数值基本相同,但在0.680<Dd<0.895 区域栏杆高0.45H的主梁脉动风压系数明显大于栏杆高0.35H,最大CP,rms差值达0.038.有栏杆时,在0.074<Dd<0.320 和0.738<Dd<0.945 动力较强区域,栏杆高0.35H的脉动风压系数幅值最小.由图9(b)可知,在主梁下表面栏杆高0.35H的脉动风压系数小于栏杆高0.45H和0.56H.有栏杆时在主梁下表面迎风侧斜腹板区域,α=+5°的脉动风压变化剧烈程度明显大于α=0°.
总体而言,在风压变化显著的区域,α=0°时栏杆高0.45H的脉动风压系数明显大于其他工况.α=+5°时栏杆高度的变化不影响主梁表面脉动风压系数的变化规律,但数值上存在明显的差异,基本上呈现出栏杆高0.45H>栏杆高0.56H>栏杆高0.35H的规律.可知,栏杆高0.35H的主梁涡振幅值小于栏杆高0.45H和0.56H,可能与脉动风压提供的动力大小有关.
3.3 脉动压力功率谱
为了更加深入地分析各测点脉动压力和模型振动之间的关联,下面分析各测点的脉动压力功率谱与模型振动功率谱的关系.图10 是主梁上、下表面各测点的功率谱,以α=+5°时主梁上表面M 测点(Dd=0.055 处)和下表面N 测点(Dd=0.846 处)为代表点分析.

图10 代表测点脉动压力功率谱(α=+5°)Fig.10 Fluctuating pressure power spectrum of representative measuring point at attack angle of +5°
由图10 可知,栏杆高0.35H、0.45H和0.56H的M 和N 测点的脉动压力卓越频率与主梁自振频率十分接近.对比其功率谱幅值,可知栏杆高0.45H时功率谱幅值最大,栏杆高0.35H时较小.无栏杆时,测点的脉动压力卓越频率与模型自振频率不同,且功率谱幅值很小.
图11 是各工况下模型表面各测点的脉动压力卓越频率.由图11可知,栏杆高0.35H时主梁表面有少部分测点的脉动压力卓越频率偏离模型自振频率;栏杆高0.45H和0.56H的主梁表面各测点有相同的脉动压力卓越频率(1.919 Hz),且与模型自振频率(1.920 Hz)相近;无栏杆时,各测点的卓越频率非常离散,且大部分测点的脉动压力卓越频率与模型自振频率相差较大.

图11 脉动压力卓越频率(α=+5°)Fig.11 Excellent frequency of fluctuating pressure at attack angle of +5°
由此可知,栏杆高度的变化会影响脉动压力卓越频率和功率谱幅值的变化,导致主梁涡激振动性能的改变.
3.4 局部升力对涡振的贡献系数
局部升力对涡振的贡献系数是由脉动风压系数和局部测点升力与涡激力的相关系数乘积得到的[14],当涡振贡献系数大于0 时,表示该局部的升力对涡振有促进作用;当涡振贡献系数小于0 时,表示该局部的升力对涡振有抑制作用.涡振贡献系数的绝对值越大,表明局部升力对涡振的影响程度越大.因此分析局部升力对涡振的贡献系数,可以充分了解栏杆高度变化对主梁局部涡振性能的影响规律.
局部升力对涡振的贡献系数的计算方法如式(2)、式(3)所示.
式中:CRi为各测点的升力对涡振贡献系数;CPi,rms是第i测点的脉动风压系数;ρi为第i测点局部升力与整体升力的相关系数;F(t)为整个模型受到的升力时程;fi(t)为第i测点升力时程.
图12 和图13 是α=0°和+5°时主梁上、下表面涡振贡献系数结果.由图12(a)可知,α=0°时,栏杆高0.45H时主梁上表面涡振贡献系数最大,其次是栏杆高0.56H和0.35H,无栏杆时最小.其中,栏杆高0.45H的主梁涡振贡献系数在整个上表面起伏变化,极大值出现在Dd=0.097 和Dd=0.886 区域,对应最大涡振贡献系数分别为0.111 和0.114.而其他三工况的涡振贡献系数基本上在0.041 以内.由图12(b)可知,栏杆高0.45H时在迎风侧斜腹板前缘(0<Dd<0.038)的局部升力对涡振有促进作用,而在迎风侧斜腹板中部区域(0.038<Dd<0.109)对涡振有抑制作用.整体上说,在0.122<Dd<0.814 区域栏杆高0.45H的局部升力对涡振的贡献程度要大于其他三者.

图12 α=0°时主梁表面涡振贡献系数分布Fig.12 Distribution of VIV contribution coefficient on girder’s surface at attack angle of 0°

图13 α=+5°时主梁表面涡振贡献系数分布Fig.13 Distribution of VIV contribution coefficient on girder’s surface at attack angle of+5°
由图13(a)可知,有栏杆时,各栏杆高度在0.074<Dd<0.320 和0.752<Dd<0.945 区域,局部升力对主梁涡振贡献均较大,其贡献值基本在0.100 以上.由图13(b)可知,在下表面斜腹板与底板交界处附近,各栏杆高度均会出现涡振贡献系数最大值.对比上、下表面涡振贡献系数的数值,可知下表面的涡振贡献系数明显小于上表面,故影响主梁涡振振幅的主要区域在上表面.
综上所述,当α=0°时,栏杆高0.45H时在主梁上表面前部和尾部区域提供了较大的涡激力,而栏杆高0.35H在该区域削弱了局部升力对涡振的贡献作用,故栏杆高0.35H时未发生涡激振动现象.当α=+5°时,各栏杆高度在上述区域局部升力均提供了较大的涡激力,故诱发了涡激振动.栏杆高度的变化影响上述区域局部升力对主梁涡振的贡献程度,当涡振贡献系数越大时,产生的涡振振幅越大.
4 结论
通过节段模型动态测压和测振风洞试验,研究了栏杆高度对流线型箱梁涡激振动性能的影响,并揭示了其影响规律及作用机理,得到的主要结论如下:
1)人行道外侧栏杆高度的变化会显著影响流线型箱梁的涡振性能,当栏杆高度为45%梁高时主梁涡振幅值最大,在此基础上适当降低或增大栏杆高度,均对主梁涡振有较好的抑制效果,降低栏杆高度效果更好.因此,在工程应用中可综合考虑功能要求和涡激振动性能,选择最优的栏杆高度.
2)有栏杆时主梁表面的脉动风压卓越频率与自振频率基本一致;同无栏杆的主梁相比,设置栏杆后主梁表面的平均风压系数和脉动压力功率谱幅值显著增大,主梁表面大部分区域的升力对涡振贡献值增大,从而导致设置栏杆后的主梁涡振振幅增大.
3)当栏杆高度变化时,主梁上表面前部和尾部、下表面迎风侧斜腹板处的脉动风压系数会发生显著变化,主梁表面的脉动压力功率谱幅值也发生明显变化,主梁局部升力对涡振的贡献因栏杆高度改变而发生变化.

