大跨混合连续箱梁桥钢混结合段传力机理试验与分析

袁辉辉 ，黄珍珍 ，吴庆雄 ，林镇海

（1.福州大学 土木工程学院，福建 福州 350116；2.工程结构福建省高校重点实验室，福建 福州 350116；3.福建农林大学 金山学院，福建 福州 350002；4.福州三江口建设发展有限责任公司，福建 福州 350007）

对于跨越通航河流、铁路和公路的预应力混凝土连续箱梁桥，为了使桥梁满足通航要求、减轻结构自重、加快施工速度，采用钢-混凝土混合箱梁桥成为一种可行的技术途径［1］.一般而言，钢-混凝土混合梁将混凝土梁段布置在主梁承受负弯矩的部位，将钢梁段布置在承受正弯矩的部位，充分发挥两种材料抗压性能和抗拉压性能优越的特点，从而形成强度高、刚度大、动力性能好的结构形式［2-3］.针对桥梁建设中钢混结合段的主要构造形式，国内外学者［4-11］通过模型试验和有限元分析发现，钢混结合段作为影响结构整体受力和安全性的关键部位，在实际设计和施工中需要确保其受力性能良好、构造细节合理、混凝土与钢结构的结合性能良好并可靠，以实现主梁整体受力和协调变形.

抗剪连接件是钢混组合结构中传递荷载的主要部件，其中应用较多的是剪力钉和PBL剪力键.剪力钉的剪切刚度对钢与混凝土界面的受力与传力影响较大［12］，而群钉效应会显著降低剪力钉平均抗剪承载力和抗剪刚度［13］，导致剪力钉传力不均匀，且剪力钉间距越大，剪力钉平均抗剪承载力越低.近年来PBL 剪力连接件在钢混结构中得到推广应用，针对PBL 剪力键的传力机理、承载能力、抗疲劳能力开展的试验研究表明［14-16］，PBL 剪力键的承载力高、延性好、抗疲劳性能优秀，钢板开孔直径、钢板板厚、贯通钢筋的大小和强度、混凝土强度等是影响剪力键极限承载力和疲劳性能的主要因素.此外，钢格室的设计参数是否合理也会显著影响结合部构造的受力性能［17-18］，如钢格室的顶板、承压板、肋板等在设计中均需重点考虑.

在钢混结合段中，钢梁顶底板、腹板和横隔板与混凝土结合后，由于钢板板厚远小于混凝土的板厚，若不采取必要措施，则钢板内的力无法及时有效地传递给混凝土，造成应力在混凝土内不能充分扩散，从而导致应力集中［19］.既有研究对象多为混合梁斜拉桥中的钢混结合段，由于斜拉索的水平分力作用，斜拉桥上的钢混结合段受力以轴压为主，而梁桥上的钢混结合段则主要承受弯矩和剪力且有正有负，受力更为复杂.马尾大桥采用了一种新型的填充混凝土的后承压板式钢混结合段构造，与既有工程及试验研究对象的构造形式存在明显差异［20］.由于钢混结合段连接部位构造及受力复杂，一旦损伤或破坏，修复难度大，从而影响整座桥梁的结构安全及使用寿命.在进行箱梁桥钢混结合段的设计时，其构造应能使结合段两侧钢箱梁和混凝土箱梁之间的内力传递顺畅，且具有良好的抗开裂性、抗疲劳性和耐久性［21］.鉴于目前大跨度混合梁桥的工程实践较少，本文依托主跨240 m 的福州马尾大桥主桥，通过室内模型试验和实体有限元分析进行马尾大桥钢混结合段受力性能研究，揭示钢混结合段的空间应力分布规律和传力机理.相关研究成果可促进钢-混凝土混合连续箱梁桥在实际工程中的进一步推广应用.

1 钢混结合段缩尺模型试验概况

1.1 钢混结合段试验模型设计

如图1 所示，福州马尾大桥横跨闽江，主桥联长（71+83+123.5+240+123.5+83+71）m=795 m，主跨跨径240 m，是目前国内最大跨度的钢-混凝土混合连续梁桥［20］.主跨跨中采用钢箱梁代替预应力混凝土箱梁，钢箱梁区段长96 m，采用单箱双室结构，顶板宽度为20.25 m，梁高为4.203～4.358 m.在混凝土箱梁与钢箱梁结合处设置总长6.5 m的钢混结合段.结合段包括长3.0 m 的钢箱梁过渡段和长3.5 m 带钢格室的混凝土箱梁段，结合面处为一厚60 mm 的承压板.结合段钢结构部分的顶板采用正交异性板，其板厚28 mm，腹板和底板的板厚均为24 mm，在距离结合面2 m处设置一道厚度20 mm的横隔板，结合处通过变高板肋进行刚度过渡，板肋与承压板焊接.上述由顶底板、腹板及加劲肋、变高度T 肋和横隔板组成的构造，主要作用是将钢箱梁集中的应力平稳地传递并扩散到内填混凝土钢格室中.混凝土箱梁段往混凝土侧采用双壁板组合构造，内、外壁板分别长2.5 m 和1.8 m；为加强钢结构与混凝土的共同作用，钢格室的顶板、底板和腹板均设有间距200 mm 的M22-150 剪力钉和间距600 mm 的PBL 剪力板.PBL剪力板开孔直径80 mm，并在孔内穿直径32 mm 的钢筋.

图1 福州马尾大桥钢混结合段构造示意图Fig.1 Schematic diagram steel-concrete joint of Fuzhou Mawei Bridge

综合考虑试验场地和加载等条件，确定节段模型几何缩尺比为1∶3.5，即钢混结合段缩尺模型的长度为6.7 m、宽度为5.8 m，各构造细节与实桥相同，如图2所示.

图2 缩尺模型构造示意图（单位：mm）Fig.2 Schematic diagram of the scaled test model（unit：mm）

试验模型与实桥采用相同材料，包括Q370q 钢材、C55 混凝土、HRB400 钢筋等，材料参数见表1.为保证预应力钢束锚固端和张拉端的布置和加工需要，需对理论缩尺截面进行部分调整，与实桥相比，调整后的主梁混凝土端截面轴压刚度和抗弯刚度分别提高了1.34 倍和1.26 倍，钢箱梁端截面轴压刚度和抗弯刚度分别提高了1.26 倍和1.21 倍.PBL 剪力板及贯穿钢筋按面积相似比设计，根据抗剪承载力相似原则选用M10-100剪力钉.

表1 结合段材料力学参数Tab.1 Mechanical properties of the joint material

1.2 缩尺模型试验加载方案

为了确定缩尺模型中的加载条件，首先采用MIDAS/Civil 软件建立如图3 所示的实桥空间杆系有限元模型，并以钢混结合段的结合面为研究对象，主要考虑表2列出的7种静力加载工况.在进行缩尺模型试验加载设计时，根据表2 所示按相似比换算后的钢混结合面内力理论值（轴力、剪力和弯矩），为了便于在试验模型的混凝土箱梁段施加较大的轴力、在钢混结合段施加效果明显的剪力和弯矩，同时为了保证大尺度试验模型的顺利吊装和安全加载，本次试验中钢箱梁端部边界设置为固结、混凝土箱梁端部设置为简支，如图4 所示，以尽量使得缩尺试验模型受力最不利的结合面准确反映实桥对应截面的受力状态.

表2 缩尺试验模型钢混结合面的内力理论值Tab.2 Theoretic values of internal forces of the key sections of the scaled test model

图3 实桥空间梁单元有限元模型Fig.3 Spatial beam FEM of the actual bridge

图4 缩尺试验模型的加载Fig.4 Loading of scaled test model

混凝土梁段施加最大轴力考虑1.2倍安全系数，主梁轴向加载按29 016 kN×1.2≈34 819 kN 设计，采用自平衡的预应力钢绞线施加荷载.模型采用与实桥相同规格的1×7-ϕs15.2 预应力钢绞线，每束钢绞线的公称横截面积为140 mm2，预应力索最大张拉应力取0.75fp＝0.75×1 860 MPa＝1 395 MPa，所需预应力索数量为34 819×103/（140×1 395）≈178束，选用12孔的夹具式锚具，所需预应力孔洞为178/12≈15 个.采用圆锚张拉端锚具，锚板直径166 mm，锚下垫板边长230 mm，对应的波纹管外径90 mm.试验模型中结合面需施加最大弯矩4 013 kN∙m，考虑1.4倍的超载后施加弯矩为5 618 kN∙m.通过在主梁模型上部布置4 个2 000 kN 竖向液压千斤顶实现弯矩加载.由于需施加的最大剪力1 344 kN 远小于最大弯矩需施加的竖向力，在试验中不再额外施加剪力.

1.3 缩尺模型试验测量方案

缩尺模型上的位移测点分布如图5 所示.其中1号截面为结合段混凝土端部，2号截面为结合段混凝土中部，3 号截面为结合面，4 号截面为结合段钢梁端部.在顶板、底板、腹板分别布置120 个、72 个、24个应变片，如图6 所示，其中，1 号截面为混凝土箱梁段测点，2～8号截面为钢箱梁段测点.腹板以第1行为例，由混凝土箱梁侧向钢箱梁侧依次编号为1-1～8-1；以1 号截面为例，由中腹板侧向边腹板侧依次编号为1-1～1-3.顶底板以第1 列为例，由混凝土箱梁侧向钢箱梁侧依次编号为1-1～8-1；以1 号截面为例，由中腹板向翼缘板端部依次编号为1-1～1-8.

图5 位移测点布置图Fig.5 Layout of displacement measuring points

图6 应变测点布置图Fig.6 Layout of strain measuring points

2 静力试验结果分析与讨论

2.1 结构整体受力性能

钢混结合段缩尺模型在整个加载过程中并未发现混凝土开裂或钢材屈服现象，直至加载结束，模型完好无损.图7 为试验模型各控制截面在不同级别荷载作用下的竖向位移曲线.由图7（a）可知当施加荷载由350 kN 逐级增至930 kN、2 550 kN、2 800 kN、4 300 kN、5 500 kN、6 650 kN 时，结合面（3 号截面）处最大竖向位移由0.35 mm 增至0.90 mm、2.66 mm、2.92 mm、4.41 mm、5.50 mm、6.30 mm，对应截面弯矩由435 kN∙m增至1 314 kN∙m、2 020 kN∙m、2 295 kN∙m、4 013 kN∙m、4 816 kN∙m、5 618 kN∙m，呈线性增长，说明模型处于弹性工作状态.由图7（b）可以看出，结合段各截面的竖向变形沿纵桥向没有明显突变，变形协调，说明此类带钢格室的结合段设计合理，保证了主梁刚度从混凝土箱梁段到钢箱梁段平稳过渡.

图7 试验模型控制截面竖向位移Fig.7 Vertical displacement at key sections of the test model

2.2 结构局部受力性能

2.2.1 箱梁顶板

本次试验的应变结果均在试验模型制作完成且施加完预应力之后测得，因此未能考虑模型自重和施加轴力的影响.由于预应力通过承压板均匀施加到结合面上，可计算得到结合面处混凝土的初始压应力为-9.5 MPa.由于数据众多，图8 仅示出顶板测点在加载过程中的应变情况.

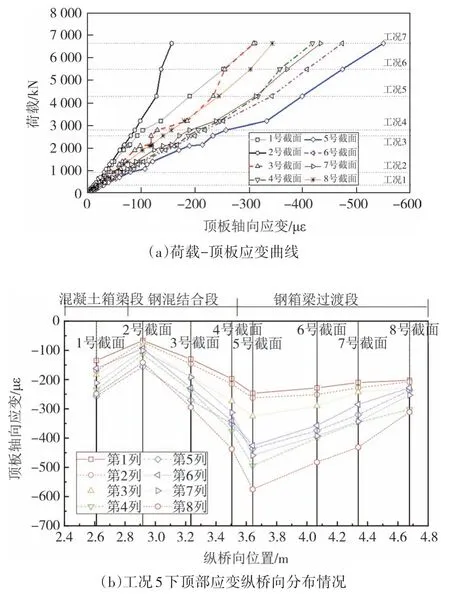
图8 试验模型顶板应变Fig.8 Top plate strains of the test model

图8（a）为各工况下顶板测点的荷载-应变曲线.可以看出，工况1～工况5 下，5 号截面最大应变增量依次为-30 με、-67 με、-190 με、-233 με和-399 με，顶板应变与荷载呈线性递增关系，说明构件处于弹性工作阶段；工况5（承载能力极限状态最大弯矩组合）下，顶板混凝土测点的应力增量为-14.1 MPa，此时顶板混凝土的最大压应力为-23.6 MPa，小于C55混凝土的抗压强度设计值24.4 MPa；顶板钢板的最大压应力为-82.2 MPa，小于Q370q 钢材强度设计值275 MPa，表明该结合段顶板混凝土和钢板强度均满足设计要求.工况6 和工况7（1.2 倍和1.4 倍承载能力极限状态）下，5号截面最大应变增量分别为-474 με和-550 με，计算得到顶板钢板的最大压应力为-97.6 MPa 和-113.3 MPa，均小于钢材强度设计值275 MPa；而顶板混凝土的最大压应力分别达到-26.4 MPa和-29.0 MPa，均超过C55混凝土的设计强度，不满足设计要求，但明显小于C55 混凝土的峰值抗压强度63.8 MPa，且结构仍处于弹性工作状态，说明该钢混结合段具有充足的安全储备.

由图8（b）所示工况5 作用下顶板各测点沿纵桥向的应变分布可以看出，顶板纵向压应变从承压板到过渡段交接处，呈由大到小的变化规律.中腹板及附近（第7、8 列），边腹板（第4 列）从4 号截面到5 号截面的应变变化较大.腹板受到约束使其变形较小，从横桥向看，钢箱梁顶板压应变呈现腹板处（第4、8列）大、翼缘板和两腹板区域小的规律.应变由5 号截面向钢箱梁侧几乎呈线性递减，表明过渡段T 肋具有良好的传力作用.钢箱梁上由2号截面到5号截面应变逐渐增大，呈线性增长，表明剪力连接件能将内填混凝土的力平稳地传递给钢格室.由于结合段的钢格室及内部填充混凝土所承担的应力通过承压板集中传递给钢箱梁过渡段，使得4号截面到5号截面应力增加较快.

2.2.2 箱梁底板

图9（a）所示为各工况下底板测点的荷载-应变曲线.各工况底板应变与荷载呈线性关系，即构件处于弹性阶段；承载能力极限状态最大弯矩组合工况下，混凝土和钢测点的最大应变增量分别为215 με 和562 με，换算得到底板混凝土的最大应力为-1.9 MPa，底板钢板的最大拉应力为115.8 MPa，结合段底板混凝土和钢板强度均满足设计要求.1.4倍承载能力极限状态工况下，混凝土和钢测点的最大应变增量分别为298 με和802 με，换算得到底板混凝土的最大应力为1.1 MPa，底板钢板的最大拉应力为165.2 MPa，分别小于C55 混凝土和Q370q 钢材的抗拉强度设计值1.89 MPa和275 MPa，仍能满足材料设计强度要求.

图9 试验模型底板应变Fig.9 Bottom plate strains of the test model

图9（b）绘制了承载能力极限状态最大弯矩组合工况下底板各测点沿纵桥向的应变分布.可以看出，底板钢箱梁应变（从2 号截面开始）呈抛物线变化.中腹板（第5 列）和边腹板（第1 列）从4 号截面到5号截面的应变变化较大，这是由于该处底板受腹板的约束，其变形较小.中腹板的4 号截面4-5#点的应变为563 με，5 号截面5-5#点的应变增至680 με，靠近边腹板的1-4#点到1-5#点应变由610 με 增至680 με，这是由于结合段的钢格室及内部填充混凝土所承担的较均匀的应力通过承压板集中传递给钢箱梁过渡段，使得该截面处底板应力增加.

2.2.3 箱梁腹板

图10 为工况7（1.4 倍承载能力极限状态工况）下腹板测点沿顺桥向的应变分布.可以看出，腹板侧的钢箱梁应变分布呈中间大、两头小的形态，在5 号截面处应变最大；由2号截面上升到5号截面再下降到8 号截面，变化接近线性且较为平缓，说明钢混结合段的腹板传力比较平顺；位于3-5#点处的腹板钢箱梁最大应变为680 με，换算应力为134 MPa，表明结构安全储备充足.

图10 试验模型腹板应变Fig.10 Web plate strains of the test model

3 实桥钢混结合段精细化有限元分析

3.1 有限元模型的建立与验证

建立的钢混结合段精细化实体单元有限元模型如图11（a）所示.使用的混凝土和钢材材料应力-应变本构关系如图11（b）所示.本文采用四折线本构模型［22］模拟钢混结合段中钢材的弹塑性行为，采用《混凝土结构设计规范》（GB 50010―2010）［23］推荐的混凝土单轴受压应力-应变关系模拟混凝土的非线性行为.根据单元选择原则和研究目的，除了钢筋采用2 维桁架单元外，模型其余部分均采用三维实体单元，且将钢梁和混凝土梁分开建模.其中，混凝土箱梁段、钢混结合段的承压板与PBL 剪力键、钢箱梁过渡段钢板的单元类型主要为8 节点线性六面体单元（C3D8R），钢混结合段的内填混凝土、钢格室钢板、剪力钉的单元类型为4 节点线性四面体单元（C3D4R）.对各个部件进行网格划分时，为防止单元大小差异过大，造成单元节点过约束，不同部件的接触面网格大小尽量接近，且变形越大的位置，网格划分越精细，防止单元过渡扭曲造成计算不收敛.

图11 钢混结合段精细化实体有限元模型Fig.11 Refined solid FEM of steel-concrete joint

由于实桥钢混结合段的结构、荷载和边界条件基本对称，为节省模型分析的计算时间，在有限元建模时采用对称建模.结构关于桥面中心线（Z轴）对称，设立对称边界XSYMM，结合面混凝土箱梁端部简支，钢箱梁端部固结.钢格室及顶底板PBL剪力板与内填的混凝土的接触采用Master-Slave 接触算法；内填混凝土与承压板之间的接触采用硬接触方式；剪力钉及腹板PBL 剪力板与混凝土接触边界设为绑定.接触属性设置中，切向采用摩尔库伦摩擦罚函数形式，参考文献［24］中的设置方法，将摩擦因数µ取为0.4，法向为硬接触，允许接触后分离.贯穿PBL 剪力板的钢筋以内置的方式嵌入内填混凝土.

在图11（a）的精细化实体有限元模型中施加与试验模型相同的边界条件和荷载，得到各工况下的荷载-位移曲线和关键部位的应变分布曲线图，并与试验结果进行对比分析，如图12 所示.由图12 可知承载能力极限状态最大弯矩工况下钢混结合段轴向应变呈现腹板处顶底板应力较大、两腹板之间和翼缘板区域应力较小的分布情况，且由钢格室往承压板方向应力逐渐增大，从承压板往钢箱梁过渡段方向应力逐渐下降，在承压板位置取得应力最大值，与前文试验结果基本吻合，说明有限元建模方法可较准确地反映结构受力性能与空间应力分布状态.

图12 有限元分析与试验结果的对比Fig.12 Comparison between FEA and test results

3.2 钢混结合段传力机理分析

实桥钢混结合段组成部件众多、构造复杂，且又同时承受轴力、剪力和弯矩的共同作用，为进一步厘清各部件的传力机理，本节继续分析钢混结合段在单独承受轴力、剪力和弯矩作用下的受力状态，其中有限元模型的边界条件设置为钢箱梁端部固结，混凝土端自由悬臂.

3.2.1 轴力传递机理

为了解实桥钢混结合段在轴力单独作用下的应力分布情况和传递规律，在图11（b）所示模型的自由悬臂端施加-1 000 kN的轴力，得到图13所示的应力分布图.以承压板的位置为起点，沿着钢格室纵向各部件所承担的轴力占比如图14所示，图中Max.Prin⁃cipal 为单元第一主应力，S33 为单元沿Z轴方向（垂直于截面）的纵向正应力.

图13 轴力作用下结合段应力分布图Fig.13 Stress distribution of joint section under axial force

图14 轴力作用下结合段各部件轴力分担比Fig.14 Component force ratio of joint section under axial force

由图13 可知，钢格室及其内填混凝土全截面受压，越靠近承压板应力越大，且顶板压应力较底板略小；承压板应力分布较为均匀，但与钢格室钢板、PBL 剪力键焊接区域存在应力集中现象，压应力相对较大.由图14 可知，混凝土箱梁段中，与承压板接触的钢格室外面板轴力占比约为20%、内面板占比约为11.5%、PBL 剪力连接件占比约为5%、剪力钉占比约为2%.承压板接触的内填混凝土因挤压作用承受约61.5%的轴力.由于PBL 剪力键、剪力钉与混凝土间的机械咬合作用，以及钢格室面板与内填混凝土的摩擦作用，内填混凝土的轴力逐渐转移至钢格室面板，距离承压板越近，钢格室面板轴力占比越大，内填混凝土轴力占比逐渐减小.钢箱梁段中，与承压板接触的钢箱梁面板轴力占比约为53%、加劲肋占比约为47%.距离承压板越远，轴力由加劲肋逐渐传递到钢箱梁面板上，钢箱梁面板的轴力占比逐渐增大，加劲肋的轴力占比逐渐减小.

3.2.2 剪力传递机理

为了解实桥钢混结合段在剪力单独作用下的应力分布情况和传递规律，在有限元模型自由悬臂端施加1 000 kN的剪力，得到图15所示的应力分布图，图中S22为单元沿Y轴方向的竖向剪应力.

图15 剪力作用下钢混结合段应力分布图Fig.15 Stress distribution of joint section under shearing force

在竖向剪力作用下，钢混结合段的钢格室腹板处内填混凝土、PBL 剪力键以及钢箱梁段腹板承受较大的剪应力；而承压板底部附近混凝土受到挤压，压应力较大.钢格室靠近承压板底部附近的钢板应力较大.剪力从钢格室内填混凝土传递到PBL 剪力键和腹板处剪力钉上，然后传递到钢格室钢板上，再通过承压板和钢格室钢板传到钢箱梁上.

3.2.3 弯矩传递机理

为了解实桥钢混结合段在弯矩单独作用下的应力分布情况和传递规律，在有限元模型自由悬臂端施加1 000 kN∙m的弯矩，得到图16所示的应力分布图.

图16 弯矩作用下钢混结合段应力分布图Fig.16 Stress distribution of joint section under bending moment

在弯矩作用下，钢混结合段钢格室内填混凝土顶板受压、底板受拉，由于有一部分应力由PBL 剪力键和剪力钉传递给钢格室面板，剩余应力直接传递给承压板，因此越靠近承压板，钢格室钢板应力越大，混凝土应力越小；承压板与钢顶板的焊接处混凝土受到挤压，导致该处混凝土应力较大.

弯矩传递可分为受压与受拉两部分区域，其中受压区域的传力路径和各部件占比与轴力作用下的基本一致，这里不再赘述；受拉区域的传力路径主要是钢混结合段的内填混凝土通过剪力钉和PBL 剪力键将大部分荷载传递给钢格室面板，而承压板受力较小.

3.3 钢混结合段构造参数分析

由上述分析可知，实桥钢混结合段的关键传力构造为承压板和剪力连接件，且承载能力极限状态荷载组合下钢结构部分的最大应力仅为115.8 MPa，距离钢材的设计强度275 MPa 还有较大优化空间.因此，本节进一步分析承压板厚度和剪力连接件布置间距对钢混结合段受力性能的影响.

3.3.1 承压板厚度

钢混结合段中的承压板易出现应力集中现象，其厚度直接关系到结构的刚度和所能承受的荷载，且会影响内力的平缓传递.实桥钢混结合段承压板厚度为60 mm，在保持其余设计参数不变的前提下，改变承压板厚度（40 mm、50 mm、70 mm、80 mm）进行钢混结合段模型的受力分析，得到表3 所示的承压板厚度不同时钢混结合段的变形和应力.当承压板厚度从40 mm 增加至80 mm 时，承压板大部分区域的应力在15 MPa 以下，最大应力先减小后增大，承压板厚度为50 mm 时最小；承压板纵向变形随之减小，其中从40 mm 增加至50 mm 时降幅最大，幅度为-17.2%；钢箱梁最大应力和竖向位移随着承压板厚度增大而逐渐减小，但降幅较小.随着承压板厚度由80 mm 减小到50 mm，钢混结合段内填混凝土的应力逐渐增大，但变化幅度不大，厚度取50 mm 时内填混凝土最大应力为-17 MPa；当承压板厚度由50 mm 降到40 mm 时，内填混凝土最大应力达到-20.3 MPa，增加了15%.因此，综合考虑受力性能和建设成本，实桥钢混结合段承压板厚度取50 mm时，构造比较合理.

表3 承压板厚度不同时主要构件性能指标Tab.3 Main performance index of key components for different thickness of the bearing plate

3.3.2 剪力钉间距

剪力钉是钢混结合段主要连接构造之一，据《公路钢混组合桥梁设计与施工规范》（JTG/T D64-01―2015）相关规定，剪力钉间距宜取直径的10～15 倍，且不宜大于300 mm.马尾大桥实桥设计采用M22-150 剪力钉，间距200 mm.为了解剪力钉间距对钢混结合段受力性能的影响，本节扩展选取间距150 mm、250 mm和300 mm进行对比分析.表4列出了剪力钉间距不同时，承压板和钢格室的变形和应力.增大剪力钉间距会导致剪力钉、承压板、钢格室的最大应力水平不同程度地增大，当剪力钉间距由150 mm增大至250 mm 时均呈现小幅度增加趋势，而间距由250 mm变化至300 mm时增幅显著增大，剪力钉和承压板最大应力增幅分别可达到12.5%和13.7%.承压板平均应力水平均在14 MPa 以下.另外，随着剪力钉间距的增大，钢格室内填混凝土的应力水平和应力集中区域也随之增大，尤其是剪力钉间距从250 mm 到300 mm 的变化较明显，间距取300 mm 时内填混凝土局部区域压应力超过-20 MPa.因此，综合考虑受力性能和建设成本，实桥钢混结合段剪力钉间距取250 mm时，构造比较合理.

表4 剪力钉间距不同时主要构件性能指标Tab.4 Main performance index of key components for different spacing of shear studs

3.3.3 PBL剪力键间距

PBL 剪力键是钢混结合段主要连接构造之一，马尾大桥实桥采用开孔直径80 mm、间距600 mm 的PBL 剪力板.为了解PBL 剪力键布置间距对钢混结合段受力性能的影响，本节拓展实桥参数，建立间距400 mm、600 mm 和800 mm 的有限元模型进行对比分析.表5 列出了PBL 剪力键间距不同时承压板和钢格室的变形和应力.随着PBL剪力键间距的增大，PBL 剪力键、承压板、钢格室的最大应力水平均随之明显增大；PBL 剪力键间距由400 mm 增至600 mm时，承压板和钢格室的最大应力分别增加了10.7%和12.4%，PBL 剪力键最大应力增幅约为3%；间距由600 mm 增至800 mm 时，增幅显著增大，PBL 剪力键的最大应力由94.4 MPa 增加到104.3 MPa，增加了10.5%，承压板和钢格室的最大应力分别增加了17.7%和21.3%.因此，综合考虑受力性能和建设成本，实桥钢混结合段PBL 剪力键间距与设计相同，取600 mm时构造比较合理.

表5 PBL剪力连接件间距不同时主要构件性能指标Tab.5 Main performance index of key components for different spacing of PBL shear connector

3.3.4 结合段构造参数优化后有限元分析

根据参数分析结果，取承压板厚度为50 mm、剪力钉间距为250 mm、PBL 剪力键间距为600 mm，建立构造参数优化后的实桥钢混结合段有限元模型，得到图17 所示承载能力极限状态下结构的应力分布.由图17可知，钢结构部分的应力都在150 MPa以内，混凝土处于全截面受压状态，压应力大部分在15 MPa 以内.根据《公路钢混组合桥梁设计与施工规范》（JTG/T D64-01―2015），对优化后的钢混结合段进行验算，发现结合段各截面的计算应力与安全系数的乘积均小于材料的设计强度，满足规范要求.

图17 构造优化后钢混结合段应力分布图Fig.17 Stress distribution diagram of steel-concrete joint after structural optimization

4 结论

以大跨度钢-混凝土混合连续箱梁桥——福州马尾大桥的钢混结合段为研究对象，开展了几何缩尺比例为1∶3.5的大比例模型静力加载试验研究，同时进行了实桥钢混结合段的精细化实体有限元分析，得到以下结论：

1）承载能力极限状态最大弯矩组合工况下，试验模型结合面最大竖向位移为4.41 mm，混凝土梁段全截面受压，结合面顶板混凝土最大压应力为-23.6 MPa，底板钢板最大拉应力为115.8 MPa，均小于设计材料C55混凝土和Q370q钢材的容许应力.

2）静力加载试验过程中钢混结合段模型并未发现明显开裂破坏现象，直至1.4倍承载能力极限状态组合工况结束模型仍完好无损，各关键截面测点的荷载-位移曲线与荷载-应变曲线基本呈线性关系，模型始终处于弹性工作状态，表明该结合段的设计具有充足的安全储备.

3）通过钢混结合段在各内力作用下的主应力分析可知，轴力和弯矩的60%通过剪力钉和PBL 剪力连接件由钢格室内填混凝土传递至钢箱梁，剩余部分直接传递到承压板；剪力通过PBL 剪力连接件和腹板剪力钉从钢格室内填混凝土传递至钢箱梁上.

4）钢混结合段空间应力分布表现为沿横桥向顶底板在与腹板连接处的应力较大，两腹板之间和翼缘板区域的应力较小；沿纵桥向钢箱梁的应力从承压板向两端逐渐减小；结合段各截面的竖向变形沿纵桥向没有明显突变，变形协调，说明带钢格室的钢混结合段传力平顺，保证了主梁刚度从混凝土箱梁段到钢箱梁段的平稳过渡.

5）综合考虑受力性能和建设成本，建议此类采用填充混凝土后承压板式的新型钢混结合段的承压板厚度取50 mm、剪力钉间距取250 mm、PBL 剪力键间距取600 mm，此时构造较为合理.