新余市不同功能区樟树土壤水分特征研究

肖 斌，罗 蓉，董星宇，段 毅

（1.中国林业科学研究院 亚热带林业实验中心，江西 分宜 336600；2.新余钢铁集团有限公司，江西 新余 338000；3.宜春市袁州区林业局，江西 宜春 336000）

樟树[Cinnamomum camphora(L.) Presl.]为樟科(Lauraceae)樟属(Cinnamomum)常绿高大阔叶乔木，是我国重要的经济树种和绿化树种［1］，在中国南部各省份广泛分布，现已成为南方许多城市生态建设的首选树种，被誉为江南宝树［2-4］。樟树在城市园林植物造景中发挥着重要的作用，其既可以呈带状分布作为行道树，或孤植成为重点观赏树种，也可以散点植配合其他树种作为点缀［5］。但随着城市化和工业化进程的加快，人类活动加速了土壤结构的破坏和功能的减弱，如土壤压实板结易导致水分滞留不透水，且因土壤利用方式的改变使得土壤环境和土壤理化性质发生了明显的变化，引起了城市化过程中不透水面积增加，加剧了城市内涝灾害，这对植被生长及城市园林绿化景观效果造成了严重影响［6-10］。以往的研究大多是针对不同功能区城市绿地或者不同植被类型土壤性质的［6，11-12］，对樟树的相关研究很少体现在城市不同功能区上。由于南方城市樟树分布面积广，受环境和人为因素的影响大，且土壤水分特征存在空间变异性，因此，研究城市不同功能区樟树的土壤水分特征，将对城市园林绿化养护、景观美化具有重要的意义。本文以樟树为研究对象，通过探讨城市不同功能区樟树的土壤水分特征，以期为城市园林绿化樟树栽培与养护提供参考性数据。

1 材料与方法

1.1 研究区概况

新余市位于江西省中部偏西，地处九岭、武功山、峰顶山三山交接地带，属于亚热带湿润季风气候。该地区具有气候温和、日照充足、雨量充沛、无霜期长、严冬较短的特征。年平均气温17.7 ℃，年平均降水量为1595 mm。夏、秋季雨水少，多干旱，冬季则多霜雪天气，常有冻害出现。境内多数山地主要由变质岩系、花岗岩、石灰岩、砂质岩等组成，森林覆盖率达55.8%。目前，新余市城市绿化覆盖率达54.1%，绿地率达52.5%，人均公园绿地面积为18.95 m2。在城市发展过程中，新余市将绿色发展贯穿于城市建设和改造的始终，种植开花树种（含绿篱色带）共26.25万棵，且人行道行道树以大樟树为主。

1.2 样品采集与处理

本研究以种植樟树的土壤为研究对象，2022年7月分别在新余市高新区、渝水区、仙女湖区选择具有地标性和代表性的工业区、校园、风景区、居住区和商业区进行采样，每个区设3个采样地，每个采样地设置3个取样点，共设置取样点45个（表1）。取样点选择在樟树占比多，种植时间久的取样地，经移除地表枯落物后，采用环刀分别取0～20、20～40 cm两层土样，每层土样3个重复。取出的环刀样及时称重，并带回实验室分别进行土壤容重、含水率、持水性、渗透性的测定。土壤容重、持水性、渗透性采用环刀法测定，含水率采用烘干法测定。

表1 采样地相关信息

带回实验室的环刀先用水浸泡12 h（水面不超过环刀上口），再去掉上盖，在上面套上一个空环刀，接口处用胶带密封以防漏水。将组装好的环刀放到漏斗上，通过渗透架固定，漏斗底下用烧杯承接。准备好计时器和量筒，控制每次注入的水量一致，依次为50、20、20 mL……，同时记录水分完全渗透下去的时间为t1、t2、t3……，一直到水分完全渗透下去所用的时间稳定保持不变为止。选取初渗率、稳渗率、平均入渗率作为研究渗透特征的指标。

初渗率(mL/min)=最初入渗时段内渗透量/入渗时间，本研究选取第1次加水50 mL作为最初入渗渗透量。稳渗率(mL/min)=单位时间内的渗透量趋于稳定时的渗透速率。平均入渗率(mL/min)=达到稳渗时的渗透总量/达到稳渗时的总时间。

通过称量土壤样品烘干前后质量的差异（105℃ 烘干至恒重），计算土壤含水率。土壤含水率(%)=土壤水分/烘干土质量×100%，土壤容重(g/cm3)=烘干土质量/环刀体积。土壤孔隙度和土壤持水性依据《森林土壤水分—物理性质的测定》（LY/T 1215—1999）的操作及计算方法。

1.3 土壤入渗过程的拟合

有关土壤水分入渗的数学模型有很多种，参照相关研究结果，分别选用了物理意义明确的Philip模型、半经验的Horton模型和经验性的Kostiakov模型对城市不同功能区樟树土壤入渗量的实测数据进行拟合。

Philip模型：

式（1）中：f(t)为土壤入渗率(mL/min)，t为入渗时间(min)，A为稳渗率(mL/min)；S为土壤吸水率(%)。

Horton模型：

式（2）中：fc、fo、k分别为稳渗率、初渗率、常数。

Kostiakov模型：

式（3）中：a、b为拟合参数。

1.4 数据统计分析

使用Excel 2016和SPSS 22.0软件对数据进行统计分析，采用单因素方差分析法(one-way ANOVA)和LSD多重检验法进行差异显著性分析(P＜0.05)，采用Pearson相关系数法进行相关性分析。数据采用相同功能区3个取样地的平均值±标准差表示，采用Origin 8.0软件进行图形绘制。

2 结果与分析

2.1 不同功能区樟树土壤容重、含水率比较分析

对城市不同功能区樟树土壤容重和含水率特征进行了分析，结果见图1。由图1可知，各功能区土壤容重均大于1.30 g/cm3。在0～20 cm土层中，居住区的土壤容重最大，达到1.57 g/cm3，其次分别为校园、工业区、商业区和风景区，其中居住区与风景区的土壤容重存在显著性差异。因居住区人流较大，儿童嬉戏踩踏时容易造成土壤板结，而风景区樟树以游客观赏为主，人为扰动较少，而且林下植被丰富、根系发达，区内树种多样化，其枯枝落叶腐化后又能改善土壤的理化性质［13］。在20～40 cm土层中，除居住区外，各功能区20～40 cm土层的土壤容重高于0～20 cm的土层的，其中工业区的土壤容重最大，达到1.59 g/cm3，其次分别为居住区、校园、商业区、风景区，不同土层、不同功能区间土壤容重的差异性不显著。各功能区土壤含水率范围在16.0%～23.2%，2个土层均以商业区含水率最高，其次为工业区和风景区，校园和居住区的土壤含水率均显著低于商业区的。

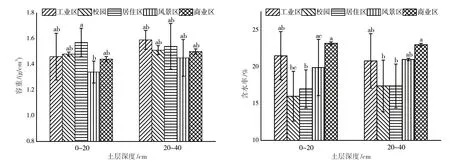
图1 不同功能区不同土层土壤容重与含水率特征

2.2 不同功能区樟树土壤孔隙度、持水性比较分析

对城市不同功能区土壤孔隙度、持水性特征进行了分析，结果见表2。由表2可知，各功能区0～20 cm土层的土壤毛管孔隙度均高于20～40 cm土层的，表明土壤表层拥有更多的水分来保障植物的生长所需。各功能区土壤毛管孔隙度范围在25.0%～41.5%，非毛管孔隙度范围在2.3%～12.4%，土壤总孔隙度范围在33.2%～48.7%。其中，风景区土壤毛管孔隙度最大，显著高于居住区的；居住区的土壤非毛管孔隙度最大，显著高于校园的；风景区的土壤总孔隙度最大，显著高于工业区的。相比而言，风景区土壤结构好、土壤容重小、总孔隙度大、土质疏松，更有利于保水保肥。从各功能区持水性特征可以看出，风景区的毛管持水量和最大持水量均为最高，除居住区外，0～20 cm土层的土壤毛管持水量和最大持水量均大于20～40 cm土层的，各功能区的毛管持水量、田间持水量、最大持水量范围分别为163.3～310.0、55.0～175.5、211.4～364.4 g/kg。

表2 不同功能区不同土层的土壤孔隙度、持水性特征

2.3 不同功能区樟树土壤渗透模型拟合情况

城市不同功能区土壤入渗速率的变化趋势总体较为一致，前期入渗速率下降快，后期逐渐趋于平稳（图2）。总体来看，0～20 cm土层土壤入渗速率高于20～40 cm土层的，表层土壤下渗速率相对较快，但当渗透量达到150 mL时，各功能区的土壤渗透速率接近0，因此在下暴雨等恶劣天气情况下，容易出现内涝现象。以前50 mL渗透量的入渗速率作为初入渗率来比较，居住区土壤入渗速率最高，0～20 cm的为303.47 mL/min，20～40 cm的初入渗率为266.08 mL/min，其他功能区土壤初入渗率均相对较低。0～20 cm土壤稳渗率以工业园最高，土壤稳渗率为5.15 mL/min，其次依次为风景区、校园、商业区、居住区；20～40 cm土壤稳渗率以商业区最高，土壤稳渗率为0.89 mL/min，其次分别为风景区、居住区、工业园和校园。

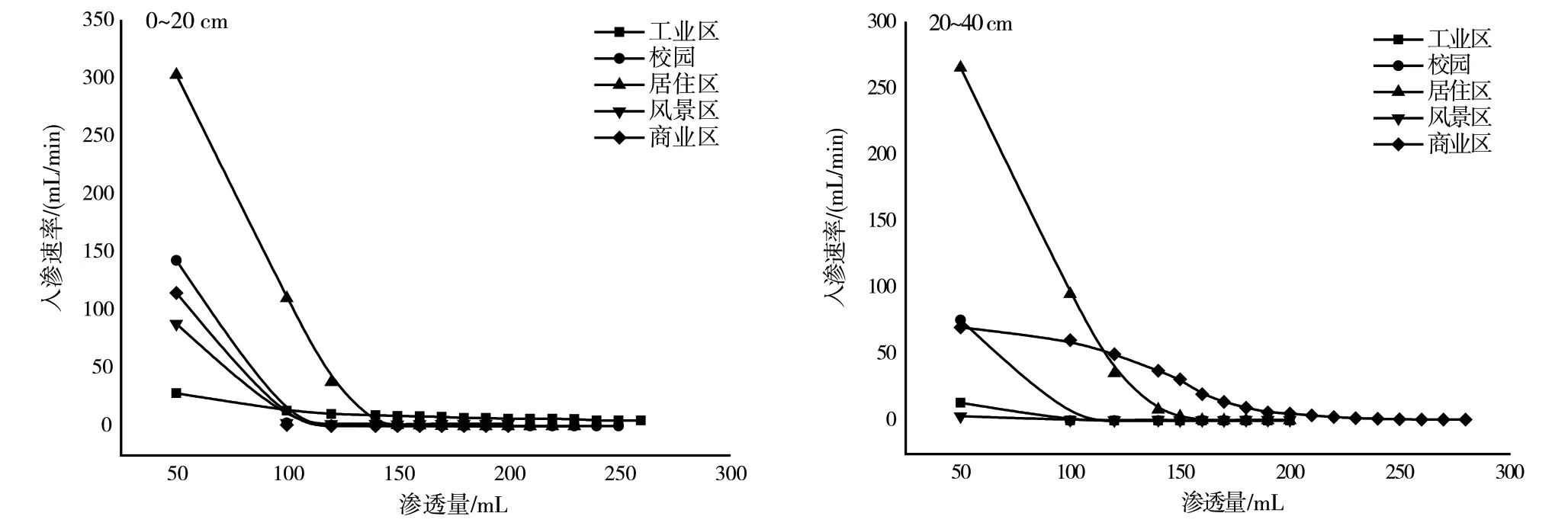
图2 不同土层、不同功能区土壤入渗特征

对城市不同功能区土壤入渗特征进行模型拟合（表3）发现，各个拟合模型的精度存在差异，Philip模型拟合的相关系数为0.854～1.000，Kostiakov模型拟合的相关系数为0.880～0.990，Horton模型拟合的相关系数为0.386～0.830。总体相比而言，Philip模型拟合效果更好，Kostiakov模型次之，Horton模型拟合效果较差。校园、居住区、风景区的土壤入渗特征用Philip模型能较好地拟合土壤水分入渗过程，工业区0～20 cm、商业区20～40 cm土壤入渗以Kostiakov模型拟合效果最佳。

表3 不同土层、不同功能区土壤入渗特征的拟合参数

2.4 不同功能区土壤水分因子相关性分析 对城市不同功能区土壤容重、含水率、孔隙度、持水性、渗透性进行相关性分析（表4）可知，土壤容重与毛管孔隙度、总孔隙度、毛管持水量、最大持水量呈极显著负相关关系，其中土壤容重与最大持水量的相关系数达到了-0.922，即土壤容重越大，土壤就越紧实，孔隙度小，其持水性也相应较差。土壤毛管孔隙度与总孔隙度、毛管持水量、田间持水量、最大持水量呈极显著正相关关系，相关系数分别为0.777、0.981、0.823、0.776；与初渗率、平均入渗率呈显著负相关关系。非毛管孔隙度与初渗率、平均入渗率呈极显著正相关关系，相关系数分别为0.779和0.778；与田间持水量呈极显著负相关性，这与非毛管孔隙度会直接影响水分下渗并吸收降水从而影响土壤水分渗透速率有关［14］。总孔隙度与毛管持水量、最大持水量分别呈显著、极显著正相关关系，相关系数分别达到了0.842、0.981。毛管持水量与田间持水量、最大持水量呈显著、极显著正相关关系，与平均入渗率呈显著负相关关系。田间持水量与初渗率、平均入渗率呈显著负相关关系。初渗率与平均入渗率呈极显著正相关关系，相关系数达到了0.925，这表明在土壤入渗过程中，初渗率直接影响到了整个入渗的平均速率，这可能与初渗率过大有关。

表4 不同功能区土壤水分因子相关性分析

3 讨论

3.1 不同功能区樟树土壤容重和含水率特征

城市不同功能区的土壤容重可以反映人类活动对土壤的压实作用程度，一般正常土壤容重约为1.30 g/cm3，当土壤容重达到1.50 g/cm3时，植物根系就难以伸入，从而影响植物的正常生长［15］。本研究表明，城市各功能区樟树土壤容重总体偏大，其中居住区0～20 cm土层的土壤容重显著大于风景区的，说明风景区土壤结构优于居住区的，风景区人为干扰相对较少，尤其是该区树种丰富、枯枝落叶多，根系发达，有利于改善土壤结构，这与李晓英等［6］的研究结果较为一致。大多数研究表明，土壤容重随土壤深度的增加而增加［16-18］，本研究居住区樟树0～20 cm土层的土壤容重高于20～40 cm的，因调查的居住区中樟树移栽时间并不长，这可能与在樟树移栽过程中人为翻耕有关。土壤含水率反映了土壤的蓄水、保水能力。本研究中商业区的土壤含水率最高，显著高于居住区和校园的，虽然商业区人为流动较为集中，但是其土壤容重相对较小，土壤疏松，透气性能好，保水能力强，这与卓文珊等［19］的研究结果不一致，可能原因是两者的土壤类型和基础地力不同，其次是新余市城区商业区人为管护、养护较好，土壤植被能得到及时有效的水分补充。

3.2 不同功能区樟树土壤孔隙度、持水性特征

土壤孔隙度与土壤容重具有反相关的特征，与容重一样，土壤孔隙度也可以用来表征土壤的压实程度，土壤孔隙度越大，土壤就越疏松［20］。本研究表明，风景区樟树的土壤毛管孔隙度和总孔隙度相较其他功能区高，土壤压实程度低，保水保肥能力好。从土壤持水性也可以看出，风景区毛管持水量和最大持水量均为最大，这与卢小遮等［21］的研究结果一致。土壤持水能力是多种因素综合作用的结果，土壤结构好能增强土壤吸附能力，更利于水分的保持。相较而言，风景区樟树土壤结构相对较好，更有利于保水保肥，以供应植物的正常生长所需。

3.3 不同功能区樟树土壤渗透特征及模型拟合

土壤入渗性能是土壤重要的物理性质，反映了土壤涵养水源和抗侵蚀的能力，是影响土壤侵蚀与地表径流的重要因素［22］。与大多数研究一致［10，23］，城市各功能区樟树土壤入渗特征为前期快，后期逐渐趋于平稳。由于土壤表层0～20 cm容重小，土壤疏松，相对于20～40 cm土层，土壤渗透速率更快。城市中的绿地削减和管理径流基本是依靠土壤入渗功能［13］，本研究表明，当渗透量达到150 mL时，土壤渗透速率变慢，若遇暴雨导致地表径流无法及时削减，则容易产生内涝现象。土壤渗透速率受多种因素影响［24］，本研究居住区樟树土壤初渗率最高，这可能与天气温度高有关。总体相较而言，各功能区樟树土壤入渗特征Philip模型拟合效果更好，这与檀海洋［25］的研究结果相一致。

3.4 不同功能区土壤水分因子相关性

土壤容重、含水率、孔隙度、持水性、渗透性都为土壤的基本物理性质，它们之间存在着一定的相关关系，本研究表明，土壤最大持水量与土壤容重、毛管孔隙度、总孔隙度、毛管持水量存在极显著相关关系，相关系数分别为-0.922、0.776、0.981、0.866，即土壤容重越大，孔隙度越小，土壤保水能力越差。土壤渗透特征用初渗率、稳渗率、平均入渗率表征，其中土壤非毛管孔隙度与土壤初渗率、平均入渗率存在极显著相关关系，相关系数分别为0.779、0.778。一般地，土壤非毛管孔隙度处于缺水状态使得土壤初始入渗率快，这与陈致富等［26］研究荒草地土壤入渗特征的结果一致。土壤初渗率与土壤平均入渗率相关系数为0.925。可见，土壤初渗率越大，土壤平均入渗率也越大。

4 结论

（1）新余市不同功能区樟树土壤容重总体偏大，其中0～20 cm土层的土壤容重表现为居住区＞校园＞工业区＞商业区＞风景区，20～40 cm土层的土壤容重表现为工业区＞居住区＞校园＞商业区＞风景区，土壤含水率范围在16.0%～23.2%，各土层不同功能区以商业区含水率最高，其次为工业区和风景区。

（2）风景区樟树的土壤毛管孔隙度、总孔隙度、毛管持水量、最大持水量相较其他功能区均为最大，相较而言，风景区樟树土壤结构相对较好，更有利于保水保肥，以供植物的正常生长所需。

（3）新余市各功能区樟树土壤入渗特征为前期快，后期逐渐趋于平稳，0～20 cm土层的土壤渗透速率快于20～40 cm土层的。总体而言，各功能区樟树土壤入渗特征以Philip模型拟合效果更好，Kostiakov模型次之，Horton模型拟合效果较差。

（4）城市不同功能区樟树土壤最大持水量与土壤容重存在极显著负相关关系、与土壤总孔隙度存在极显著正相关关系，相关系数分别为-0.922、0.981；土壤非毛管孔隙度与土壤初渗率、平均入渗率存在极显著正相关关系；土壤初渗率与平均入渗率之间存在极显著正相关关系。