运动副分布顺序对并联机构运动学与动力学性能的影响

沈惠平 仲 锐 李 菊 李 涛

(常州大学现代机构学研究中心, 常州 213016)

0 引言

三自由度纯平移和纯转动并联机构在抓取及调姿等方面已有较多的研究与应用[1],但具有转动和移动特性混合的并联机构研究和应用相对较少。

HUNT[2]于1983年设计了一种含寄生运动的3-DOF空间机构,ZHANG等[3]对2T1R的平面并联机构类型进行了综合并实现了模块化设计,但缺少对机构的运动学分析;刘艳敏等[4]研究了2T1R机构的综合方法,并优选了部分新机型;余顺年等[5]提出了一种以两平移一转动并联机构为主体的新型中医推拿机器人机型,并求出其运动学正反解的解析解;WANG等[6]提出了一种Cylindrical型两平移一转动并联机构;杨宁等[7]根据基于螺旋理论对两平移一转动型并联机构的结构综合进行研究;REFAAT等[8]根据位移李群理论对三自由度运动并联机构进行型综合研究;张彦斌等[9]根据线性变换理论,对无奇异完全各向同性2T1R型空间并联机构进行型综合;杨廷力等[10-11]基于单开链单元对2T1R型并联机构进行了型综合,得到多种含有平面闭回路结构的新型机构;SHEN等[12]设计并分析了一类具有解耦运动和符号式位置正解的2T1R并联机构,并研究了优化支链布置对运动学、动力学和刚度的影响;TETIK等[13]利用回路方程的雅可比矩阵确定了3-RRS并联机构的奇异性;SUN等[14]使用边界搜索方法求解了3-PRS并联机构的工作空间;LI等[15]对3-PRS使用数值搜索方法对并联机构的可达工作空间进行了分析。上述大部分2T1R并联机构很少具有运动解耦性[16-18]及符号式位置正解[19-20],使得机构运动学建模以及误差分析、刚度分析以及动力学分析等方面较为困难,计算量大。

机构动力学分析方法中,拉格朗日法[21-22]通过动能及势能推导来建立动力学方程,其表现形式相对简单,但在解决多杆件机构时计算量较大;牛顿-欧拉法[23]将待分析机构拆分开,建立相对应完整的动力学模型,对于构件较多的机构,分析较繁琐、计算量大;而虚功原理法[24-25]通过系统的虚位移做功建立机构动力学模型,只需要计算较少速度矩阵,具有高效、便捷的特点。基于虚功原理的力分析序单开链法[26]能求出驱动副反力(矩)外,还能求解出机构运动副中的作用力。

本文根据基于方位特征方程(POC)的并联机构拓扑设计理论方法[11],设计两种零耦合度的2T1R并联机构,它们具有相同运动副类型和数目,但在支链中的分布顺序不同,对这两种机构的主要拓扑特性(POC集、自由度、耦合度)进行分析;根据基于拓扑特征的运动学建模方法,求解两种并联机构的位置正反解;基于位置正解求解各自的工作空间与奇异性;又根据基于雅可比矩阵求解两种并联机构动平台中心点的速度与加速度曲线,根据基于虚功原理的力分析序单开链法对两种机构进行动力学建模,求解各自的驱动力;对比分析两种新型机构的运动学、动力学性能,得到其一为优选机构,并给出优选机构应用场景的概念设计。

1 机构设计和分析

1.1 机构设计

1.1.1支链设计

机构动平台POC集计算式[11,24]为

(1)

(2)

式中MJk——第i个运动副POC集

Mbi——第i条支链末端POC集

MPa——机构动平台POC集

(1)混合支链Ⅰ设计

2-DOF的两滑块平面五杆机构(P1⊥R11‖R12‖R13⊥P2)如图1a所示。为便于阐述,在静平台0上建立坐标系oxyz,x轴方向平行于P1轴线方向,y轴方向垂直于P1轴线方向,z轴方向平行于静平台0法线方向。取R12轴线上一点为基点,显然,其末端构件能够产生平行于xoz平面的两维移动(2T)以及平行于y轴的一维转动(1R),即其POC为2T1R。

图1 两种混合支链

由式(1)可得,该子并联机构末端输出的POC集为

在子并联机构的输出转动副R12的输出轴上串联一个与其同轴线的转动副R3,即转动副R12与R3是复合铰链,再在垂直于R3的轴线上串联一个转动副R4(即R4⊥R3);且用转动副R4连接动平台1的一端,从而得到混合支链Ⅰ1(图1b)。

在子并联机构输出转动副R12的输出轴上串联一个与其同轴线的转动副R3,即转动副R12与R3是复合铰链;再在垂直于R3的轴线上串联一个轴线相平行的转动副组R4、R5(即R4⊥R3),且R4‖R5,且用转动副R5连接动平台1的一端,从而得到混合支链Ⅰ2(图1c)。

由式(2)可知,混合支链Ⅰ1、Ⅰ2上末端转动副R4、R5轴线上一点的POC集分别为

(3)

(4)

式(3)表明,混合支链Ⅰ1末端的输出运动为xoz平面内的两维移动(2T)以及绕转动副R4、R12轴线的两维转动(2R);式(4)表明,混合支链Ⅰ2末端的输出运动为三维移动(3T)以及绕转动副R5、R12轴线的两维转动(2R),因设计目的是两平移一转动,故需设计另一条约束支链来分别约束支链Ⅰ中多余的运动元素,以满足其设计目标。

(2)混合支链Ⅱ设计

为使机构具有较好的承载能力及刚度,混合支链Ⅱ采用包含由4个转动副组成的平行四边形机构(简称:Pa机构),且至少包含2T1R运动元素的支链结构。

将移动副P3与Pa机构一短边串联的转动副R5刚性连接,且移动副P3的轴线与转动副R5相互平行;又在该Pa机构对边短杆上串联另一个转动副R6,使转动副R6与动平台1另一端连接,这样,组成另外一条混合支链Ⅱ1。因此,混合支链Ⅱ1可记作{-P3‖R5(-Pa)‖R6-},如图2a所示。

图2 混合支链Ⅱ的设计

同样,将移动副P3与Pa机构的一条短边平行且刚性连接,在Pa机构的另一边短杆再串联转动副R6,使转动副R6的轴线与R5相互平行布置,且用转动副R6连接动平台1的另一端,从而组成混合支链Ⅱ2。因此,混合支链Ⅱ2可记作{-P3(-Pa)‖R6-},如图2b所示。

对于混合支链Ⅱ1,由式(2)可知,混合支链Ⅱ1末端构件上R6轴线外任一点的POC集为

M3=MP3∪MPa∪MR5∪MR6=

因此,混合支链Ⅱ1末端构件能够产生三维移动(3T)和平行于转动副R6的一维转动(1R)。

对于混合支链Ⅱ2,由式(2)可知,混合支链Ⅱ2末端构件上R6轴线上任一点的POC集为

M4=MP3∪MPa∪MR6=

因此,混合支链Ⅱ2末端构件能够产生平行于xoz平面的二维移动(2T)和平行于转动副R6的一维转动(1R)。

1.1.2机构构成

使混合支链Ⅰ1中的移动副P1、P2与混合支链Ⅱ1中的P3平行布置,且将设计的混合支链Ⅰ1与混合支链Ⅱ1相互配合,混合支链Ⅰ2与混合支链Ⅱ2组合,分别并行地连接于静平台0与动平台1之间,得到的机构A与机构B如图3所示。机构A动平台前端转动副R4在Y向的位置不变,而机构B动平台后端转动副R6在Y向的位置不变。混合支链Ⅰ都含有五杆机构,混合支链Ⅱ都含有Pa机构,但其支链拓扑结构的局部稍有不同,而运动副类型及总数均相同。

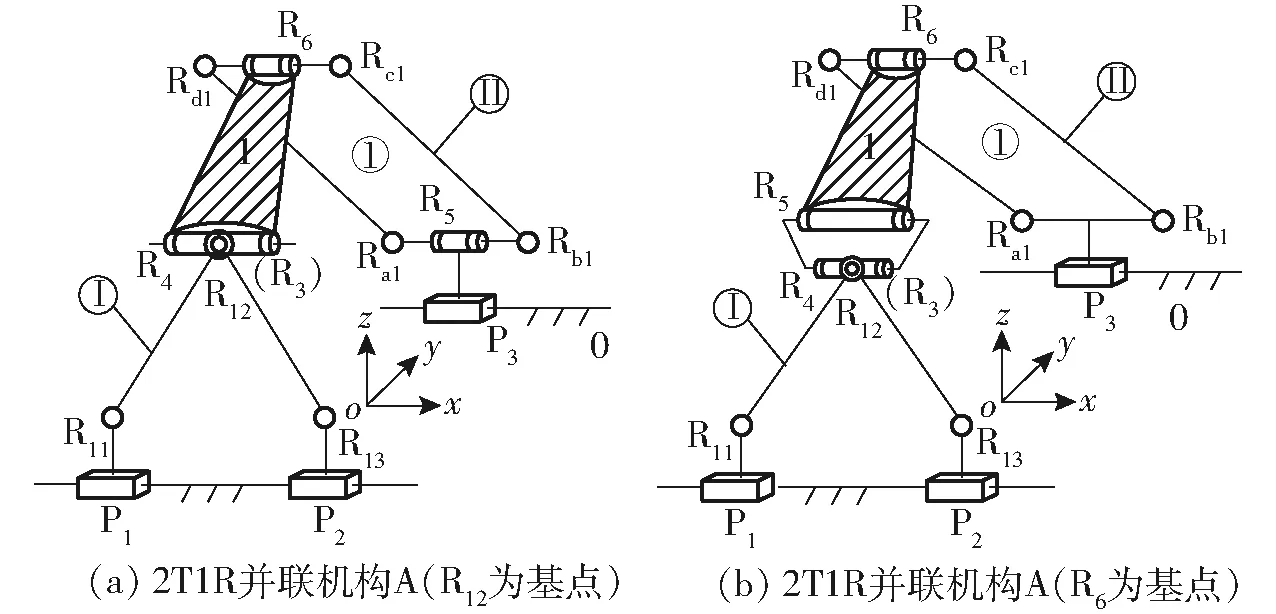
图3 两种2T1R并联机构

根据式(1)可知,2T1R并联机构A动平台1上R4轴线上一点的POC集为

MPa1=M1∩M3=

同样,2T1R并联机构B动平台1上R6轴线上一点的POC集为

MPa2=M2∩M4=

1.2 机构自由度计算

机构全周自由度计算公式[11,24]为

(5)

(6)

v=m-n+1

式中F——机构自由度

fi——第i个运动副的自由度(不含局部自由度)

m——机构所含的运动副数

v——独立回路数

n——机构所含的构件数

ξLj——第j个回路的独立位移方程数

Mb(j+1)——第j+1条支链末端构件的POC集

对机构A、B而言,显然,第1条回路为平面五杆机构(子并联机构),易知,其独立位移方程数ξL1为3,由式(5)可知,该子并联机构自由度为

而第2回路有所不同,对于并联机构A,第2回路由上述子并联机构、转动副组(R3⊥R4)与混合支链Ⅱ1{-P3‖R5(-Pa)‖R6-}构成,其独立位移方程数ξL2由式(6)计算为

ξL2=

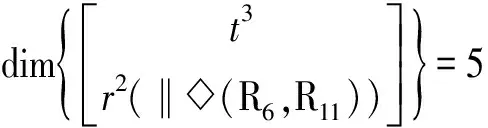
故并联机构A的自由度F2由式(5)计算为

对于并联机构B,第2回路由上述子并联机构、转动副组(R3⊥R4‖R5)与混合支链Ⅱ2{-P3(-Pa)‖R6-}构成,其独立位移方程数ξL3由式(6)计算为

故并联机构B自由度F1由式(5)计算为

机构自由度为3,因此,当取静平台0上的移动副P1、P2、P3为驱动副时,动平台1可以实现xoz平面的两维移动和绕转动副R4轴线的一维转动的输出运动。

1.3 耦合度计算

由基于单开链(SOC)组成原理[11]可知,任何一个机构都可分解为约束度为正、零、负的3种有序单开链(SOC),第j个SOCj的约束度[11,18]为

(7)

式中mj——第j个SOCj的运动副数

Ij——第j个SOCj的驱动副数

一组有序的v个SOC可划分为若干个最小的子运动链SKC,每个SKC仅含一个自由度为零的基本运动链(BKC),SKC的耦合度κ,其计算式为

(8)

对于并联机构A,其两个回路的SOC约束度由式(7)分别计算为

由SKC的判定准则[11,24]可知,并联机构A包含有2个SKC,其中,SKC1为P1⊥R11‖R12‖R13⊥P2,SKC2为R3⊥R4‖R6‖Pa‖R5‖P3,其耦合度由式(8)计算为

而对于并联机构B,两个回路的SOC约束度由式(7)分别计算为

由SKC的判定准则[11,24]可知,并联机构B包含有2个SKC,其中,SKC1为P1⊥R11‖R12‖R13⊥P2,SKC2为R3⊥R4‖R5‖R6‖Pa‖P3,其耦合度由式(8)计算为

表明两种机构均只包含2个SKC,其耦合度κ为0,因此,机构符号式位置正解可由独立求解2个SKC而得。

1.4 运动解耦性与基于SKC的机构拓扑解析

并联机构A、B的拓扑结构解析式[18]可表示为

(9)

(10)

对上述两种并联机构的拓扑分析表明:这两个机构的动平台均可实现xoz运动平面内的两维移动(2T)以及绕x轴(平行于转动副R4轴线)的一维转动,其自由度均为3。这两个机构的耦合度为零,进而无须设定虚拟变量,可直接求解得出其位置正解。动平台基点(对机构A而言为R4,对机构B而言为R6)在y轴方向的位置分量为定值。并联机构A在xoz平面内x轴方向和z轴方向的两维移动(x、z)由SKC1中的移动副P1、P2决定,机构A的转动角由移动副P1、P2、P3共同决定;并联机构B在xoz平面内x轴方向的一维移动(x)由SKC1中的移动副P1、P2决定,而在xoz平面内z轴方向的一维移动以及转动角由移动副P1、P2、P3共同决定;因此,并联机构A具有较好的部分运动解耦性。

2 并联机构运动学分析

2.1 位置分析

2.1.1机构A正逆解分析

机构A的运动学模型如图4所示,其位置正解求解归纳为:已知求驱动副输入量x1、x2、x3,求动平台1基点位置O′(x,y,z)及姿态角α。

图4 并联机构A运动学建模

设静平台0两导轨之间的距离为2a,静坐标系Oxyz原点O位于两导轨的几何中心处,x轴平行于A1A2,y轴垂直于A1A2,z轴由右手螺旋法则确定。在动平台1中转动副R4(图4a中点C3)的中心建立O′x′y′z′坐标系,x′轴与静坐标系x轴平行且方向一致,y′轴与静坐标系y轴平行且方向一致,z′轴与静坐标系z轴平行且方向一致。

设A1B1=A2B2=A3B3=l1,B1C1=B2C2=l2,C3D=l3,DB3=l4,动平台姿态角为α,如图4b所示。

(11)

该机构中C1、2、3D∈B3在yoz面的投影,如图4b所示。

因此,可以得到

(12)

由杆长约束条件DB3=l4,可得

(13)

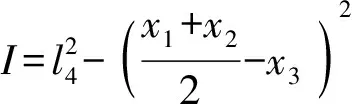
N1=2Hl3N2=-4al3

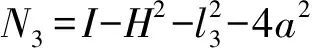
式(13)中m=±1,所以正解数目为2×1=2。

而机构的位置逆解求解可归纳为:已知动平台1的位置O′及姿态角α,求驱动副输入量x1、x2、x3。

由杆长约束条件DB3=l4及位置正解,可得

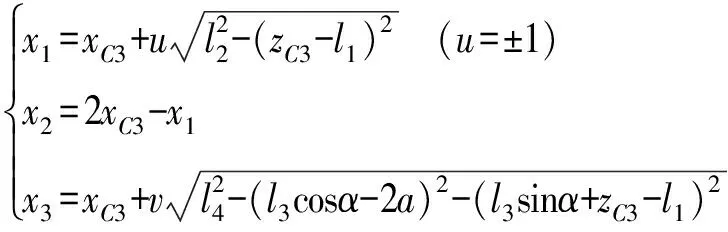
(v=±1)

(14)

由于式(14)中u=±1,v=±1,所以正解数目为2×2=4。

2.1.2机构B正逆解分析

机构B运动学模型如图5所示。

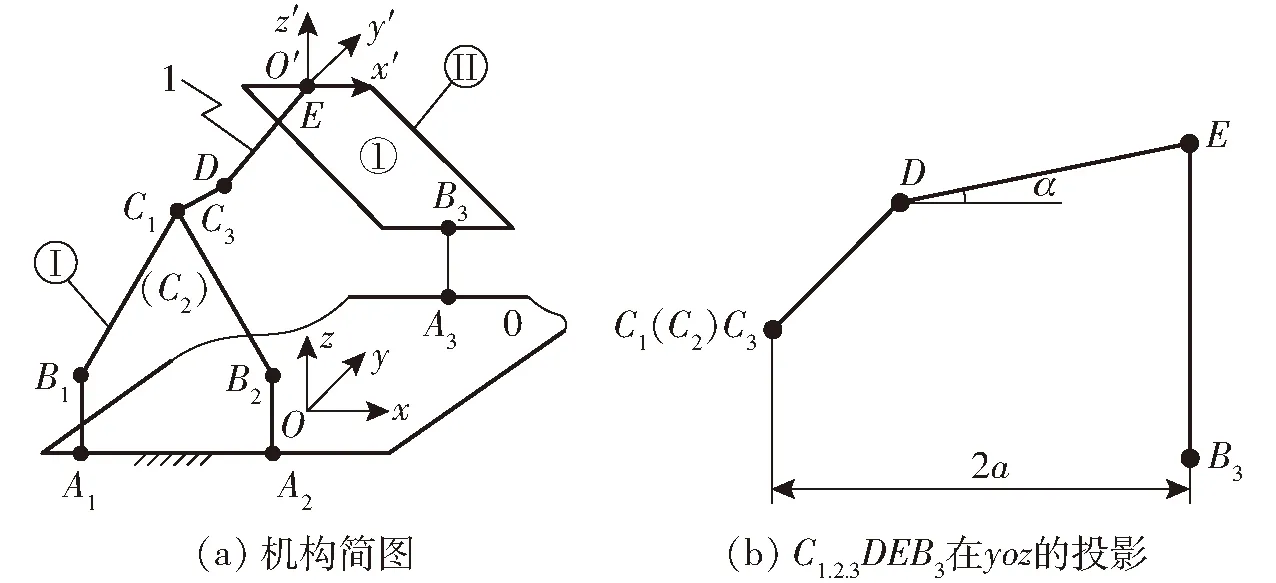
图5 并联机构B运动学建模

机构B静坐标Oxyz建立同机构A。在动平台1中转动副R6(图5a中点C3)的中心建立O′x′y′z′坐标系,x′轴与静坐标系x轴平行且方向一致,y′轴与静坐标系y轴平行且方向一致,z′轴与静坐标系z轴平行且方向一致。

设A1B1=A2B2=A3B3=l1,B1C1=B2C2=l2,C3D=l3,DE=l4,EB3=l5,动平台姿态角为α,如图5b所示。

由杆长约束条件DE=l4,可得

(15)

其中

N1=4al4N2=2Jl4

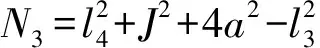
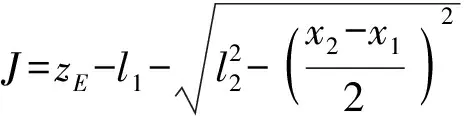
由于式(15)中m=±1,n=±1,因此正解数目为2×2=4。

进一步,逆解可由位置正解得

(16)

其中

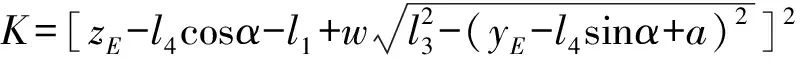
(w=±1)

(17)

由于式(16)、(17)中u=±1,v=±1,w=±1,因此反解数目为2×2×2=8。

2.1.3正逆解验算

设并联机构A尺寸参数为:a=300 mm,l1=100 mm,l2=200 mm,l3=450 mm,l4=320 mm。取3个驱动量x1=-106.09 mm,x2=181.67 mm,x3=-70.29 mm。将上述参数代入正解式(12)、(13)得到动平台的位置正解,如表1所示。

表1 运动学正解的理论计算值

表1中的2组数据对应的构型图如图6所示。

图6 机构A的正解及其对应的构型

将以图6a构型(即表1中序号1对应的构型)作为机构A的后续运动学、动力学计算对象。

将在正解中表1中的序号1数值代入式(17),得到的4组反解如表2所示,其所对应4个构型如图7所示。

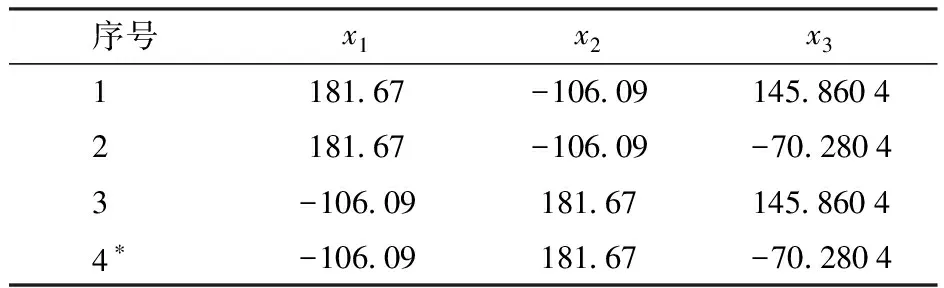
表2 运动学反解的理论计算值

图7 机构A的反解及其对应的构型

可见,表2中序号4参数与设定的机构输入参数以及图6a与图7d所示构型一致,从而验证了正逆解公式的正确性。

设并联机构B的尺寸参数为:a=300 mm,l1=100 mm,l2=200 mm,l3=180 mm,l4=450 mm,l5=320 mm。用同样的方法,验证了机构B位置正逆解公式的正确性。

2.2 工作空间

工作空间表示动平台操作端的运动范围,是并联机构的一个重要运动学指标[24-25]。因并联机构A、B均具有符号位置正解,故采用位置正解来计算工作空间。相比于通过位置逆解及预设工作空间的搜索范围、搜索所有满足约束条件的点以形成三维图的方法,该方法直接搜索驱动副的范围以确定工作空间,具有计算量少、工作空间计算准确等优点[24]。

2.2.1并联机构A

确定机构A中3个驱动移动副P1、P2和P3的移动量稍大于机构杆件移动范围,分别取为-250 mm≤x1≤0 mm,0 mm≤x2≤250 mm,-300 mm≤x3≤300 mm。通过Matlab软件,对正解式(14)～(16)进行编程,得到该机构动平台上质心的三维工作空间如图8a所示;而工作空间xyz中3个不同方向的投影如图8b～8d所示。

图8 并联机构A工作空间及其在xOy、yOz、xOz面的投影

工作空间在x=60 mm、y=-85 mm、z=300 mm平面上的截图,如图9所示。

图9 并联机构A工作空间内xyz方向上的截面图

2.2.2并联机构B

同样,确定机构B中3个驱动移动副P1、P2和P3的移动范围同机构A。通过Matlab软件,对正解式(15)进行编程,得到该机构动平台上质心的三维工作空间,如图10a所示;而工作空间xyz3个不同方向的投影,如图10b～10d所示。

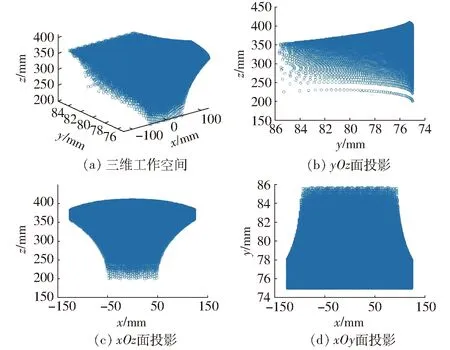
图10 并联机构B工作空间及其在xOy、yOz、xOz面的投影

工作空间在x=50 mm、y=213 mm、z=385 mm平面上的截图,如图11所示。

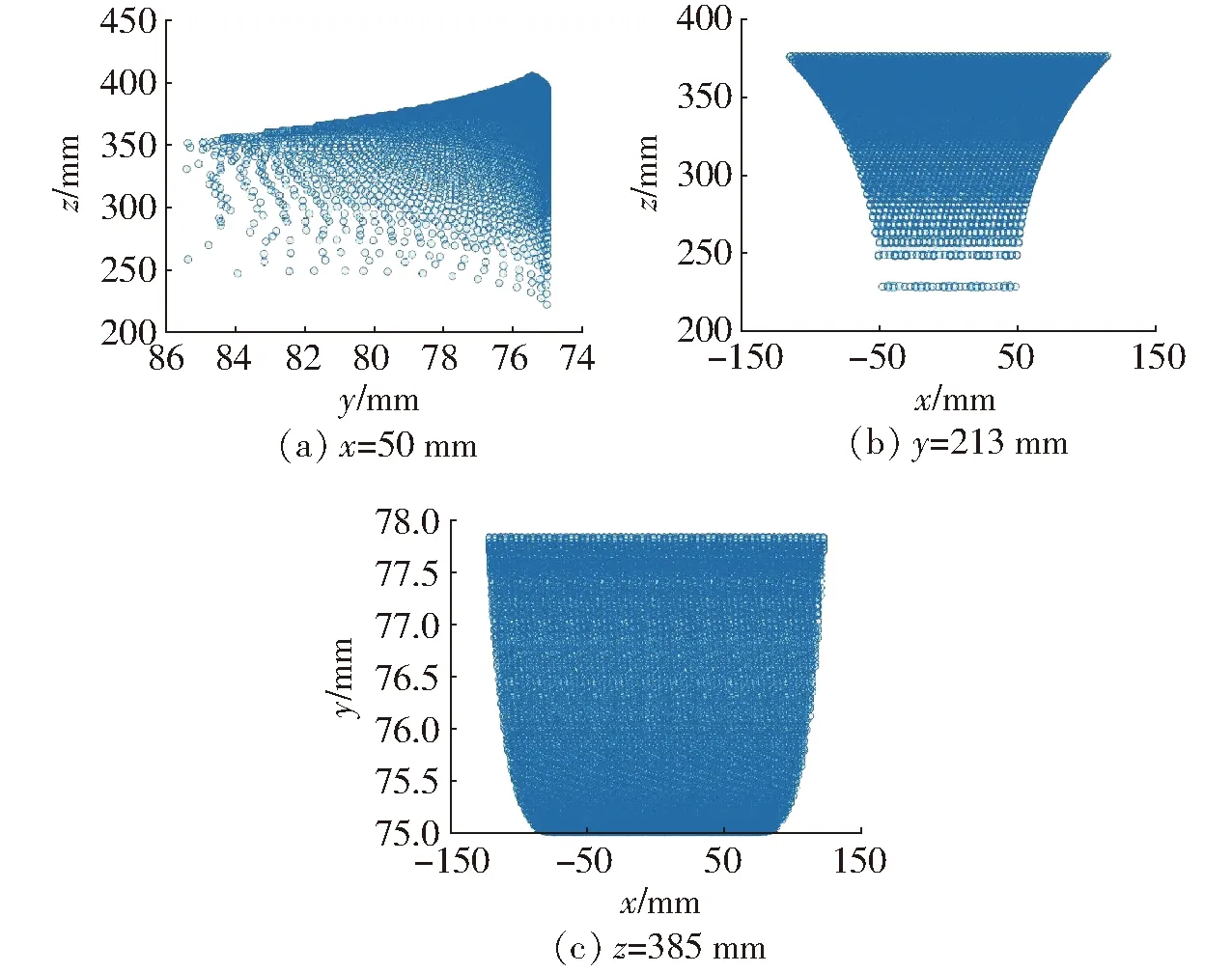
图11 并联机构B工作空间内xyz方向上的截面图

2.3 奇异性分析

采用基于雅可比矩阵的奇异位形及分析方法。雅可比矩阵为[26-27]输入关节速度到机构末端输出速度的映射,由于矩阵内部元素与位置有关,该映射关系为

(18)

式中Jo、Ji——输出、输入雅可比矩阵

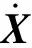
根据Jo和Ji矩阵是否奇异,将机构分为3种奇异类型:①当det(Ji)=0时,机构发生输入奇异。②当det(Jo)=0时,机构发生输出奇异。③当det(Ji)=det(Jo)=0时,机构发生综合奇异。

2.3.1并联机构A

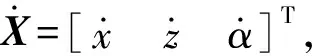
(1)输入奇异

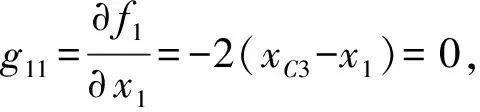
图12 输入奇异位置

(2)输出奇异

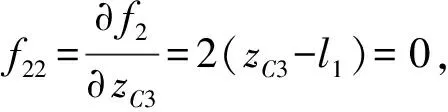
图13 输出奇异位置

(3)综合奇异

当det(Ji)=det(Jo)=0时,即输入、输出奇异同时存在,机构才发生综合奇异,经分析该机构不发生综合奇异。

2.3.2并联机构B

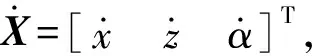
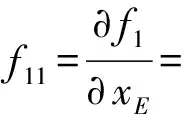
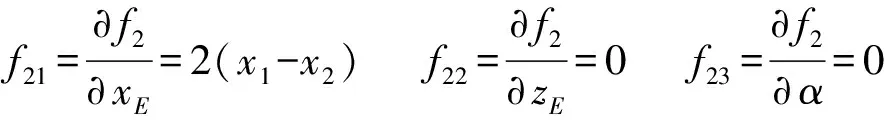
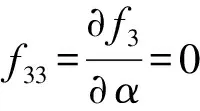
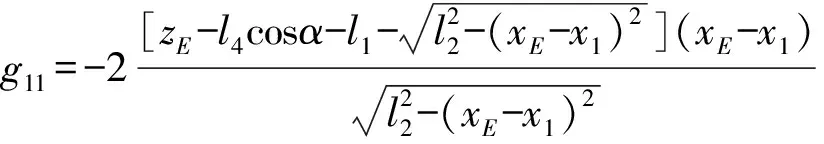
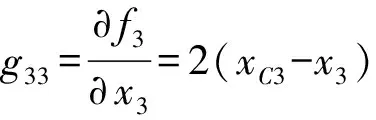
(1)输入奇异

图14 输入奇异位置1

图15 输入奇异位置2

(2)输出奇异

(3)综合奇异

当det(Ji)=det(Jo)=0时,机构才发生综合奇异;经分析发现该机构不发生综合奇异。

3 机构动力学分析

3.1 并联机构A

因机构A、B的耦合度均为零,因此这两个机构各杆件的速度和加速度均可由刚体运动学速度(加速度)合成定律求得,其分析计算流程图如图16所示。

图16 机构速度、加速度分析流程图

取3个驱动副P11、P21、P31的输入函数分别为y1=20sin(πt)、y2=-10sin(πt)、y3=20sin(πt),且3个驱动副的初始位置分别为ρ1=-131.07 mm、ρ2=181.55 mm、ρ3=-57.74 mm。

利用Matlab得到机构A动平台质心的速度与加速度的理论计算曲线如图17所示。

图17 机构A动平台质心速度、加速度理论计算曲线

在ADAMS软件中对虚拟样机进行仿真,得到机构A动平台的质心的速度与加速度仿真曲线如图18所示。

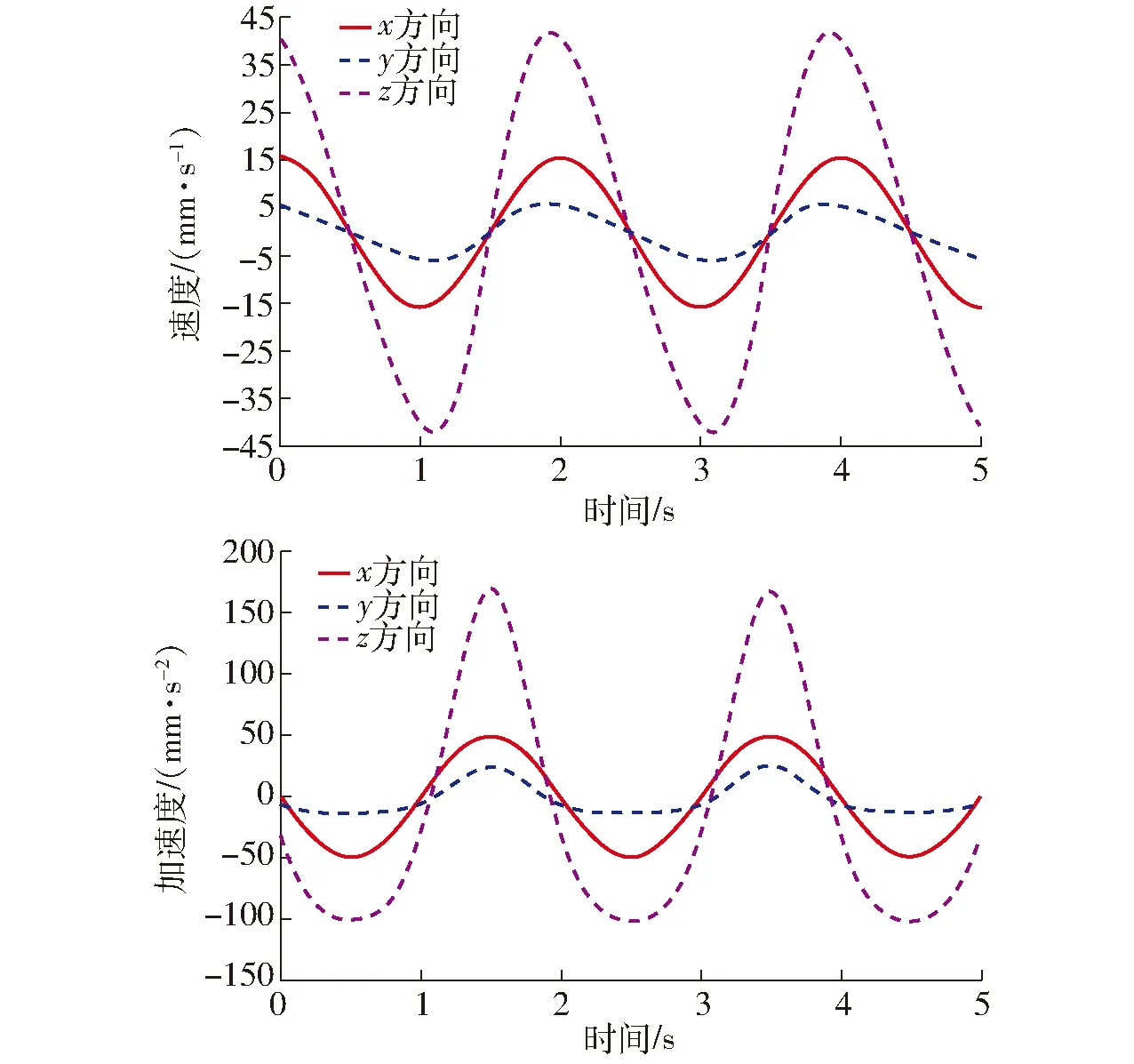
图18 机构A动平台质心速度、加速度仿真曲线

3.2 并联机构B

3个驱动副P11、P21、P31取相同的输入函数及3个驱动副的初始位置,利用Matlab得到机构B动平台质心的速度与加速度的理论计算曲线如图19所示。

图19 机构B动平台质心速度、加速度的理论计算曲线

在ADAMS软件中对虚拟样机进行仿真,得到机构B动平台的质心的速度与加速度仿真曲线如图20所示。

图20 机构B动平台质心速度、加速度的仿真曲线

从图17、18及图19、20可知,并联机构A、B理论计算的速度与加速度曲线与ADAMS仿真得到的曲线一致,表明其运动学建模求解的正确性;动平台1质心的速度与加速度曲线变化平缓,没有陡增陡减的突变现象发生,表明该机构A、B运动性能良好,均有潜在利用价值。

3.3 机构动力学建模

3.3.1基于虚功原理的力分析序单开链法

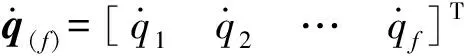
3.3.1.1并联机构A

(1)SKC2内各构件受力分析

取动平台质点为点P,则有

(19)

式中fp——动平台质心外力

τp——动平台质心外力矩

mp——动平台质量

Ip——动平台惯性矩阵

ε1——动平台角加速度

ω1——动平台角速度

a1——动平台线性速度

g——重力加速度

由驱动副A3B3受力分析可得

(20)

其中

式中f3——驱动副P3驱动力

mA3——驱动副P3质量

aA3——驱动副P3加速度

由转动杆DB3受力分析可得

(21)

式中mDB3——转动杆DB3质量

IDB3——转动杆DB3惯性矩阵

(2)SKC1内各构件受力分析

由驱动副AiBi受力分析可得

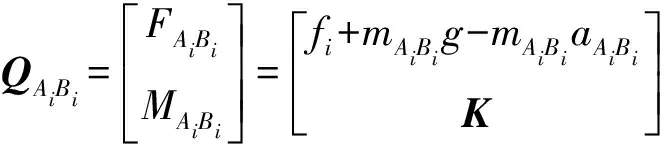
(i=1,2)

(22)

式中fi——驱动副AiBi驱动力

mAiBi——驱动副AiBi质量

aAiBi——驱动副AiBi加速度

由转动杆BjCj受力分析可得

(j=1,2)

(23)

式中mBjCj——转动杆BjCj质量

IBjCj——转动杆BjCj惯性矩阵

3.3.1.2并联机构B

(1)SKC2内各构件受力分析

取动平台质点为点P,则有

(24)

由驱动副A3B3受力分析可得

(25)

由转动杆DB3受力分析可得

(26)

(2)SKC1内各构件受力分析

由驱动副AiBi受力分析可得

(27)

由转动杆BjCj受力分析可得

(j=1,2)

(28)

由转动杆C3D受力分析可得

(29)

式中mC3D——转动杆C3D质量

IC3D——转动杆C3D惯性矩阵

3.3.2动力学方程建立

3.3.2.1并联机构A

解除两个SKC在点C3的运动副约束之后,支反力FC3转化为未知外力,根据基于虚功原理的力分析序单开链法分别建立SKC1、SKC2动力学方程为

(30)

(31)

其中

δxAiBi=JvAiBiδq(i=1、2、3)

δxBjCj=JvBjCjδq(j=1、2)

δxDB3=JvDB3δqδxp=JvpδqδxDC3=JvDC3δq

δθB1C1=JωB1C1δqδθB2C2=JωB2C2δq

δθp=JωpδqδθDB3=JωDB3δq

将式(19)～(23)代入式(30)、(31)即可求出两个SKC连接处点C3处的支反力。

3.3.2.2并联机构B

解除两个SKC在点E的运动副约束之后,支反力FC3转化为未知外力,同样可建立SKC1、SKC2动力学方程为

(32)

(33)

将式(24)～(29)代入式(32)、(33)即可求出两个SKC连接处点C3处的支反力。

3.4 机构动力学的验证与仿真

3.4.1并联机构A

设机构A中各杆件的质量分别为:mA1B1=0.056 93 kg;mA2B2=0.056 93 kg;mA3B3=0.067 27 kg;mB1C1=0.072 01 kg;mB2C2=0.070 42 kg;mC3D=0.494 4 kg;mDB3=0.105 86 kg;mRaRb=0.071 83 kg;mRcRd=0.062 41 kg。各杆件转动惯量如表3所示。

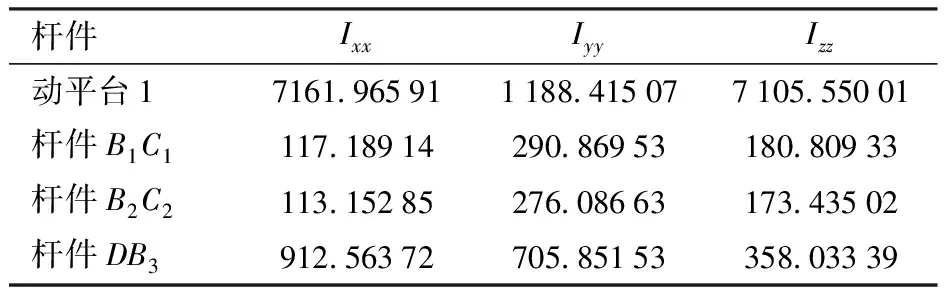
表3 机构A各杆件转动惯量

将上述参数代入动力学方程式(19)～(23),取3.1节(忽略摩擦时)该机构在负载5 kg(fp=50 N,τp=0)状态下的驱动力,如图21所示。

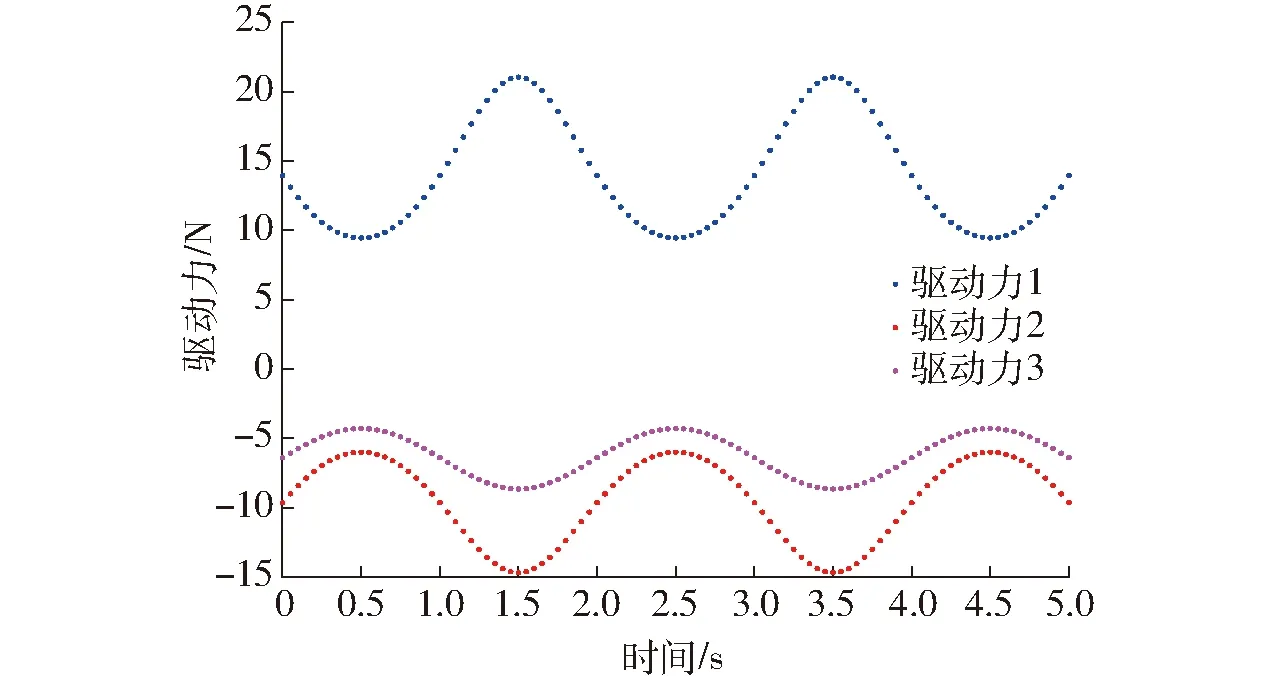
图21 并联机构A驱动力理论曲线

将虚拟样机导入ADAMS中,选取运动仿真时间为5 s,得到的驱动力仿真曲线如图22所示。

图22 并联机构A驱动力仿真曲线

3.4.2并联机构B

设机构B中各杆件的质量分别为:mA1B1=0.056 93 kg;mA2B2=0.056 93 kg;mA3B3=0.124 90 kg;mB1C1=0.072 01 kg;mB2C2=0.070 42 kg;mC3D=0.494 4 kg;mDE=0.494 4 kg;mRaRb=0.105 67 kg;mRcRd=0.063 78 kg。各杆件转动惯量如表4所示。

表4 机构B各杆件转动惯量

将上述参数代入动力学方程式(24)～(29),取3.2节的输入函数作为驱动副的输入函数,运用Matlab计算(忽略摩擦时)该机构在负载5 kg(fp=50 N,τp=0)状态下运动副处的驱动力,如图23所示。

图23 并联机构B驱动力理论曲线

同时,将虚拟样机导入ADAMS 中,选取运动仿真时间为5 s,得到的驱动力仿真曲线如图24所示。

图24 并联机构B驱动力仿真曲线

对比图21、22以及图23、24易知,驱动力理论计算曲线与ADAMS仿真曲线基本一致,即两种机构动力学模型是正确的,仅存在微小差距,其主要原因在于:各运动副连接处存在间隙,理论计算的参数值与实际模型的参数值有差距;以及ADAMS软件仿真是基于 Lagrange方程建立的动力学仿真模型,而本文主要采用基于虚功原理的序单开链法,在计算时存在舍入误差和累计误差。

4 应用场景概念设计

将设计的2T1R机构A应用于水果深加工的智能分拣、传送工艺中,其应用场景概念设计三维图如图25a所示,工作平面示意图如图25b所示,空间结构布置简图如图25c所示。其工作原理是:

图25 应用场景的概念设计

(1)传送带1以速度v0将等待分拣加工的装筐苹果送至指定位置,2T1R并联机构在传送带1的末端等待承接苹果,通过扫描识别装筐苹果的品质标签,以速度v1进行运输,待运输到相对应品质的生产线时,并联机构通过动平台的斜坡将装筐苹果滑动到下一环节的传送带上。①品质略有瑕疵的装筐苹果通过动平台转运到传动带2上,以速度v2进入苹果深加工车间。②品质较好的装筐苹果通过动平台转运到传送带3上,以速度v3进入封装出货车间。

(2)当导轨上的驱动移动副P1、P2、P3取相同速度大小和方向时,可实现长距离的移动,以使传送带1上的装筐苹果通过传送带2将瑕疵苹果或通过传送带3将高品质苹果送至相应的库存或相应环节进一步的加工。

(3)当导轨上的驱动移动副P1、P2、P3取不同速度大小和方向时,动平台可实现xOz平面内的二维移动和绕转动副R4的一维转动,其中,x轴方向和z轴方向的移动由P1、P2决定(可以调节动平台x、z位置),而转动角的转动由P1、P2、P3共同决定(可以使动平台与传送带2、3之间位置对应一致,并在y轴方向上靠近传送带1、2、3)。

5 结论

(1)根据基于方位特征(POC)方程的并联机构拓扑结构设计理论与方法,设计两种零耦合度且部分运动解耦的(2T1R)并联机构,它们具有相同运动副类型和数目,但在支链中的分布顺序不同;分别对两种机构的自由度、耦合度等主要拓扑特性进行分析,结果表明这两种机构耦合度为零。

(2)根据拓扑特征运动学分析方法对两个机构进行了运动学建模,验证了机构具有符号式位置正解;且均具有部分运动解耦性,但机构A部分运动解耦程度更好;分析了这两种机构的工作空间及其奇异位置,表明机构A在相同的杆长和工作范围条件下,工作空间更大。

(3)求解了两种并联机构动平台中心点的速度与加速度曲线,表明这两种机构动平台质心的速度与加速度曲线变化平缓,没有陡增陡减的突变现象发生,具有良好的机构运动性能;同时根据基于序单开链虚功原理对该机构进行逆向动力学建模,并求得其驱动力变化幅度相似且平缓,表明这两种机构在实际应用中电机选型的多样性。

(4)不同运动副分布顺序对并联机构运动学与动力学性能有较大影响;机构A的运动解耦性更好、工作空间更大,因此,选取机构A为优选机构;同时,对机构A用作水果深加工中智能分拣、传递的应用场景进行了概念设计。