灌区用水优化模型参数全局敏感性分析与不确定性优化
姜 瑶 颜泽文 黎良辉 闫 峰 熊吕阳
(1.南昌大学工程建设学院, 南昌 330031; 2.南昌大学鄱阳湖环境与资源利用教育部重点实验室, 南昌 330031)
0 引言
灌溉是保障粮食生产的关键,尤其在干旱地区。在水资源短缺背景下,确保合理配置灌区水资源,提高农业用水效率具有十分重要的意义[1]。灌区水资源优化配置是实现灌区高效用水的有效手段之一。随着相关研究的发展,灌区水资源优化配置逐渐由单一目标向多目标发展,由小尺度向大尺度过度,由传统优化算法[2-4]向智能优化算法[5-7]发展,由确定性优化向不确定性优化发展[8-9]。优化模型的复杂性随之增加,所涉及不确定性参数众多,从而影响了此类模型的计算效率和实用性。
模型参数敏感性分析是一种研究模型输入因素对输出变量影响程度的方法,能很好地识别影响模型性能的关键参数,在模型参数率定、参数相关性和不确定性量化等方面都发挥重要作用[10]。模型参数敏感性分析通常分为局部敏感性分析和全局敏感性分析[11]。局部敏感性分析相对简单,只检测单个参数的改变对模型的影响,但其忽略了其他因素交互作用对模型结果的间接影响,因此该方法存在一定局限性[12]。全局敏感性分析能够同时考虑多个参数变化以及参数间交互作用对模型结果的影响,更适用于具有复杂非线性特征的灌区优化问题,相关方法包括Morris筛选法[13]、EFAST(Extended Fourier amplitude sensitivity test)方法[14]、Sobol方法[15]、LH-OAT(Latin hypercube-One factor at a time)方法[16]和GLUE(Generalized likelihood uncertainty estimation)方法[17]等。参数敏感性分析方法在水文模型模拟研究中已得到广泛应用[18-19],同时在泵站系统优化中也有部分应用[20-21],但在灌区水资源优化配置研究中的应用尚不多见。灌区水资源优化配置模型涉及的参数众多,而且由于环境、地物类型、管理等因素变化的影响导致大多数参数具有不确定性。当前研究多是直接选择某些不确定性参数并对其进行定量表征,缺少对模型参数的敏感性分析,这一方面可能忽略某些敏感性因素的影响,另一方面,过多不确定性参数的定量表征会使得模型结构复杂,增加求解过程的难度,降低模型计算效率和应用效果。因此,将敏感性分析方法应用到灌区水资源优化配置中,筛选出高敏感性的关键参数,以此进行不确定性下的灌区用水优化具有重要意义和实用价值。
本文将LH-OAT方法与灌区用水优化模型耦合,建立针对优化模型参数的全局敏感性分析方法,并以黑河流域中游盈科灌区为案例研究区,定量分析模型中不确定性参数的敏感性,筛选出高敏感性参数,以此进行不确定性下的灌区用水优化,获得研究区考虑不确定性的灌溉用水配置方案。通过优化模型参数的全局敏感性分析,综合考虑高敏感性参数及其不确定性对优化结果的影响,从而降低模型的复杂性,提高模型效率和实用性,为不确定性下的灌区水资源优化配置提供方法参考。
1 研究方法
1.1 LH-OAT方法
随机OAT(One factor at a time)方法是MORRIS[13]在Monte Carlo的基础上提出的。该方法原理为:若有M个参数,每次对一个参数进行随机微小扰动,其他参数不变,共进行M次扰动,模型运行M+1次,即可得到M个参数各自的敏感度。然而,由于Monte Carlo方法随机抽样,产生大量样本导致OAT方法的运算量变大。
针对Monte Carlo会产生大量样本的问题,MCKAY等[22]在其基础上提出了拉丁超立方(Latin hypercube,LH)抽样法。该方法将整个参数空间等分成N层,对每个参数抽样N次,并保证参数在每一等分层中抽样1次,随机组成N个LH参数组。LH抽样法减少了样本数量,确保了敏感性分析的高效性,但仍存在一些缺点,即当所有参数都变化时,并不能明确是哪一参数输入值的变化引起的输出结果的变化。
LH-OAT敏感性分析法将LH抽样法和OAT敏感度分析方法相结合,克服了LH抽样法和OAT方法的不足,减少了模型运行的次数和时间,也提高了准确性,有效地反映出模型输出结果随模型参数的微小改变而变化的敏感性程度。假设有M个参数,首先将这些参数空间等分成N层,然后在每一层中抽样1次即1个LH抽样点(包含M个参数的集合),共生成N个LH抽样点。然后对每个LH抽样点中的参数采用OAT方法扰动,即每次随机改变1个参数,共有M次扰动。因此,1个LH抽样点可生成M+1个参数组,N个LH抽样点生成N×(M+1)个参数组。将模型运行N×(M+1)次,得到各参数的N次敏感度,将其取算术平均值后即可得到全局敏感度,其原理公式为
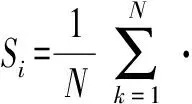
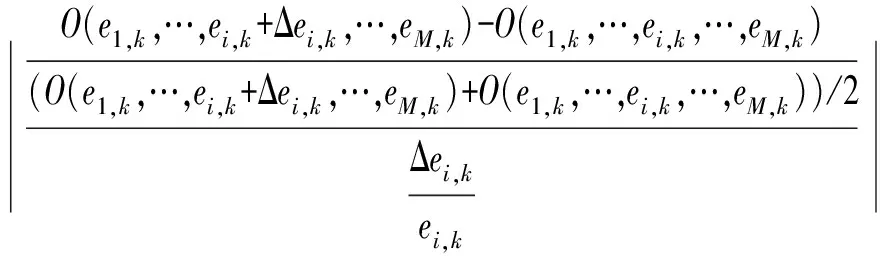
(1)
式中O——输出变量
ei,k——第i个参数在第k个LH抽样层中的取值
Δei,k——参数ei,k的某次扰动
Si——参数i的全局敏感度
1.2 优化模型
本文中的灌区用水优化模型在JIANG等[23]构建的区域灌溉用水优化模型基础上改进得到。该优化模型具有2层结构,第1层为非线性规划模型,以求解各子系统内灌溉用水和种植面积在不同作物-土壤单元间的最优分配问题;第2层采用动态规划方法来优化灌溉用水在不同子系统之间的分配。有关模型的结构与数学表达详见文献[23]。本文在原模型基础上,参考JIANG等[24]提出的方法,进一步对其结构进行了改进以提高模型效率,主要包括:①第1层所采用的各作物-土壤单元的作物水分生产函数(Crop water production function,CWPF)利用农业水文模型(SWAP-EPIC)与优化算法耦合的模拟-优化模型得到,相较于原模型中的现状CWPF,其代表了各作物-土壤单元内的最优CWPF。②第2层采用基于各单元最优CWPF优化得到的各子系统用水-灌溉效益最优响应函数。有关该模拟-优化方法详见文献[24]。给定灌区总灌溉水量,模型从第2层开始依次求解,最终可得到各层最优结果。
1.3 方法构建
将LH-OAT方法与灌区用水优化模型耦合,对优化模型中的不确定性参数进行全局敏感性分析。耦合基于Matlab程序实现,具体步骤包括:①基于所构建灌区用水优化模型,选择模型中的M个不确定性参数,并分别确定其取值空间。②采用LH抽样法对选取的M个参数在值域内进行采样,共生成N组抽样点(每组包含M个参数)。③采用OAT方法逐一对每组抽样点中的参数进行扰动,生成N×(M+1)个参数组。④以各参数组作为优化模型输入,以优化模型的不同优化结果作为输出变量,重复运行优化模型N×(M+1)次。⑤按式(1)计算各参数针对不同输出变量的全局敏感度并排序,同时统计同一参数考虑所有输出变量的敏感度全局排序。⑥根据敏感度全局排序,选择高敏感性参数并将其在合理范围内进行随机采样和组合,以此作为优化模型的不确定性输入参数,重复运行优化模型,最终得到灌区用水的不确定性优化结果(图1)。
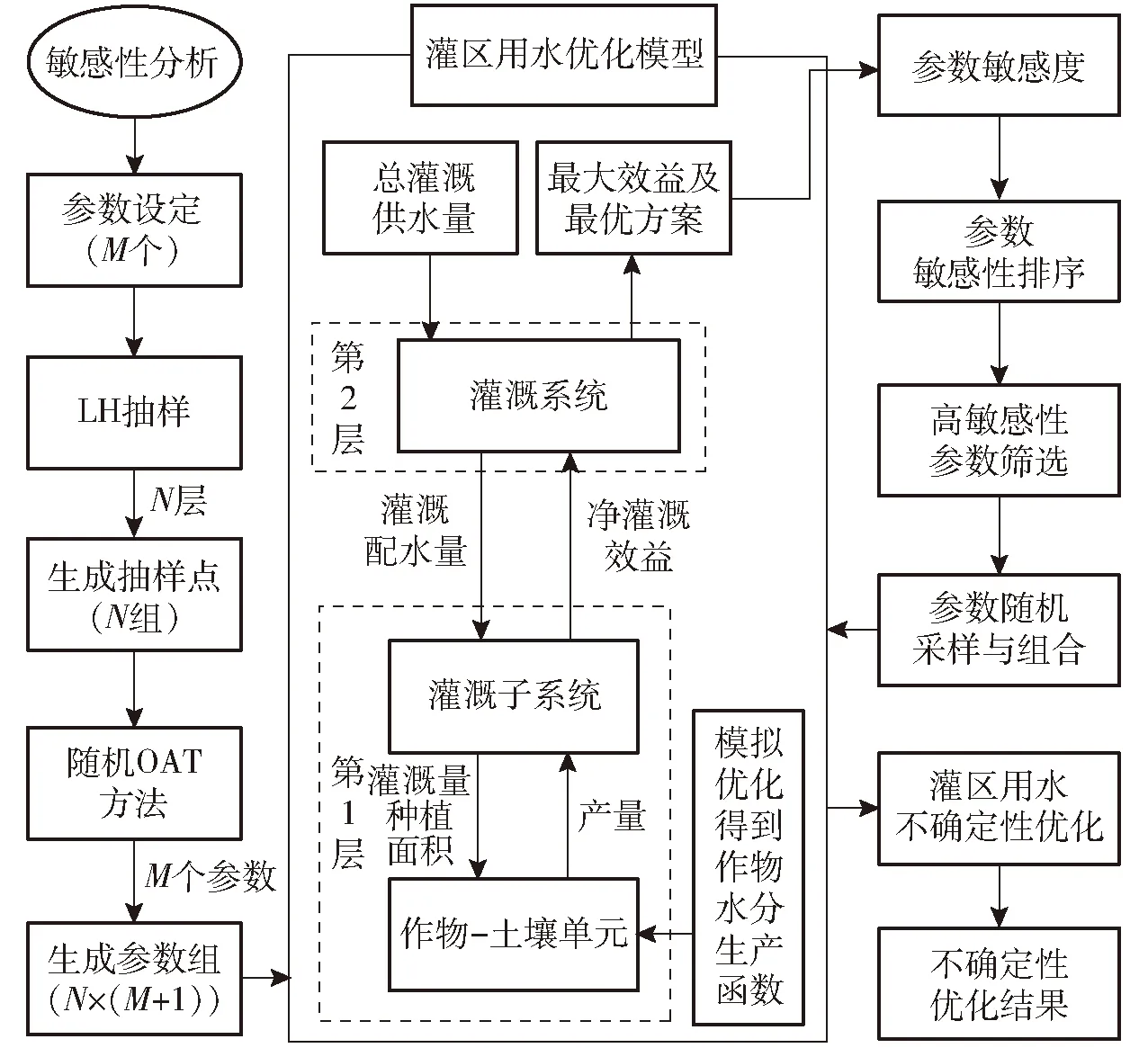
图1 LH-OAT方法与灌区用水优化模型耦合示意图
2 案例分析
2.1 研究区概况
以我国西北内陆黑河流域中游盈科灌区作为案例研究区(图2)。盈科灌区为黑河流域中游绿洲的三大灌区之一,位于甘肃省张掖市,总面积192 km2,其中灌溉面积约131 km2,占总面积的68%。盈科灌区属温带大陆性干旱气候,冬夏较长且冬季寒冷干燥,春秋较短且多风少雨。灌区年平均气温 6.5~8.5℃,日照时数达3 000 h以上,多年平均降雨量仅为133 mm,无霜期140 d左右。灌区耕作层(0~140 cm)土壤质地主要以粉壤土和壤土为主,灌区上游(西南部)的耕作层底部也常出现砂砾石层[25]。灌区内主要种植玉米、春小麦和一些经济作物,其中粮食作物种植面积约占总种植面积的83%,经济作物以蔬菜为主,包括包菜、辣椒等,面积占15%左右[26]。盈科灌区灌溉渠系由1条主干渠、2条分干渠以及1 000多条下级分配渠道组成,由盈科干渠从东总干渠引黑河水进行灌溉,灌溉方式以漫灌或传统畦灌为主。盈科灌区渠系及作物土壤分布见图2。
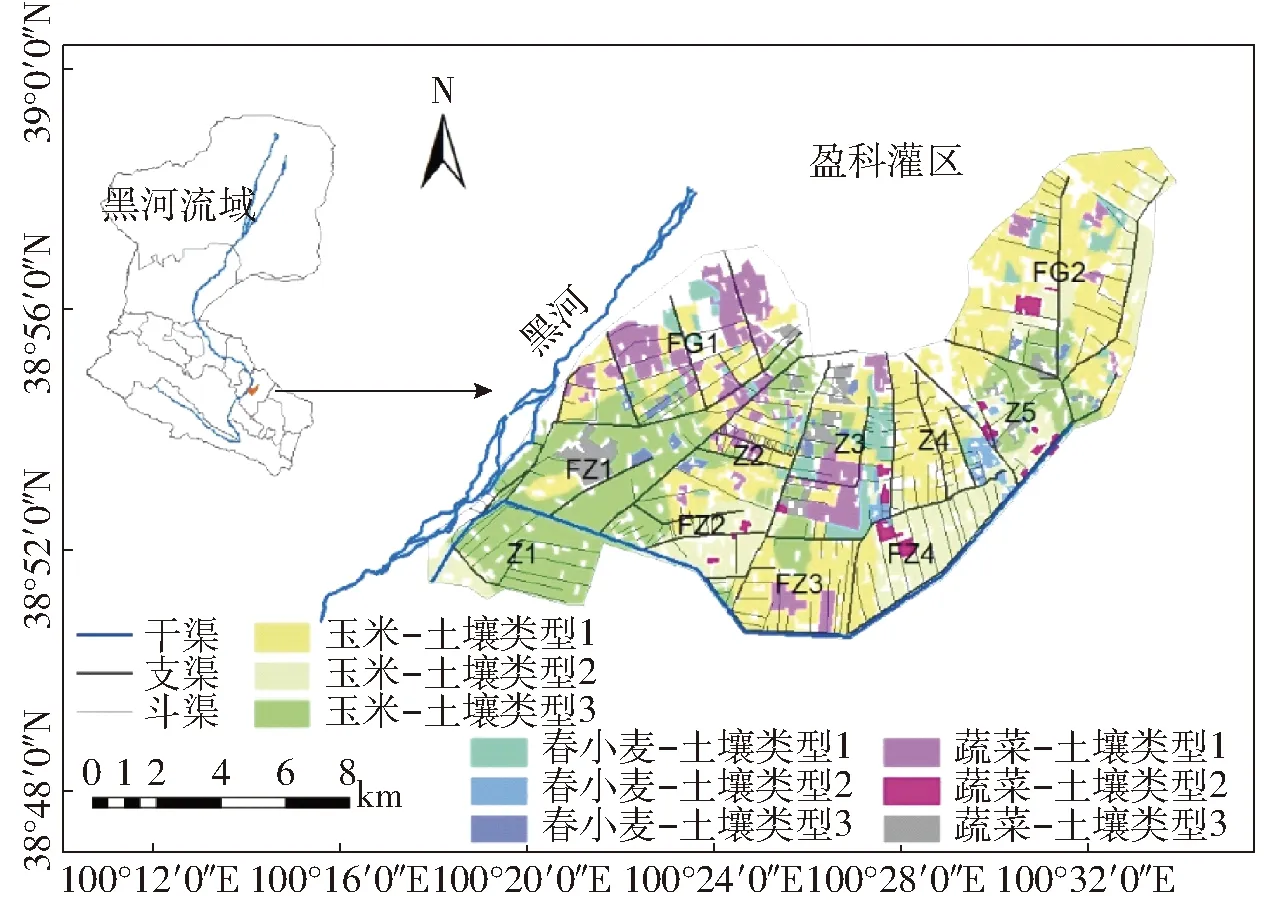
图2 盈科灌区渠系及作物-土壤单元分布图
2.2 模型参数设置
根据以往研究[23],灌区内土壤可分为3种类型,即粉壤土(0~140 cm)、壤土(0~140 cm)和粉壤土(0~60 cm),分别定义为土壤类型1~3。作物主要考虑玉米、春小麦和蔬菜(以包菜为代表)。根据灌区内3种土壤类型和作物的空间分布,共定义9种作物-土壤单元(图2),对应9种类型CWPF(表1)。根据灌区渠系分布,共定义11个渠系控制区(图2),作为优化模型第2层的子系统,各渠系控制区包含不同的作物-土壤单元,其内不同作物-土壤单元之间的优化为优化模型的第1层。优化模型中各参数设置参考文献[23]。

表1 作物水分生产函数(CWPF)类型及其对应单元
为分析模型中不确定性参数的敏感性,共选取6类参数进行分析,分别为CWPF、水价、作物价格、作物种植成本、灌溉量约束和总可用灌溉水量(地表水和地下水),共计25个参数。其中,CWPF考虑由气候变化引起的函数本身的不确定性,针对9种作物-土壤单元,分别利用1.2节所述模拟-优化模型[24]获得不同气候类型(适宜和不适宜)下的最优CWPF,其中,适宜和不适宜气候年份参考文献[24]分别采用2012年和2010年。以这2年的气象数据驱动模拟-优化模型,从而确定各单元CWPF变化的上下限,如图3(不同CWPF所对应土壤-作物单元及其分布见图2和表1)所示。其他不确定性参数根据其现状实际值进行上下浮动一定比例确定其取值空间,如表2所示。敏感性分析的输出变量设定为优化模型的目标值——净灌溉效益G和决策变量——作物灌溉量X和作物种植面积A。对25个参数分成10层进行LH抽样(即M=25,N=10),对每个LH抽样点采用OAT方法,模型总运行次数为10×(25+1)次,针对不同输出变量,根据式(1)计算每个参数对应的敏感度。

表2 模型待分析参数及其取值
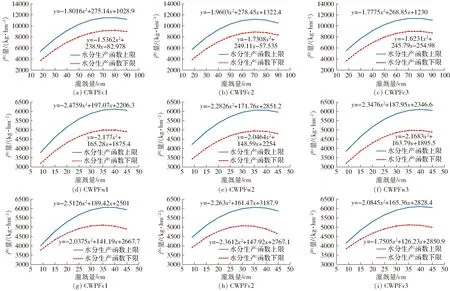
图3 盈科灌区不同作物-土壤单元内作物水分生产函数
2.3 敏感性分析结果
针对不同输出变量,计算得到25个参数的全局敏感度(图4)及其排序(表3),将各参数对不同输出变量的敏感度排序最小值作为其敏感度全局排序(表3)。参考文献[16]及参数敏感度全局排序结果,将参数敏感性划分为4个等级,排序为1的定义为极敏感参数,排序为2~5的为较敏感参数,排序为6~10的为一般敏感参数,排序在11及以后的为不敏感参数。
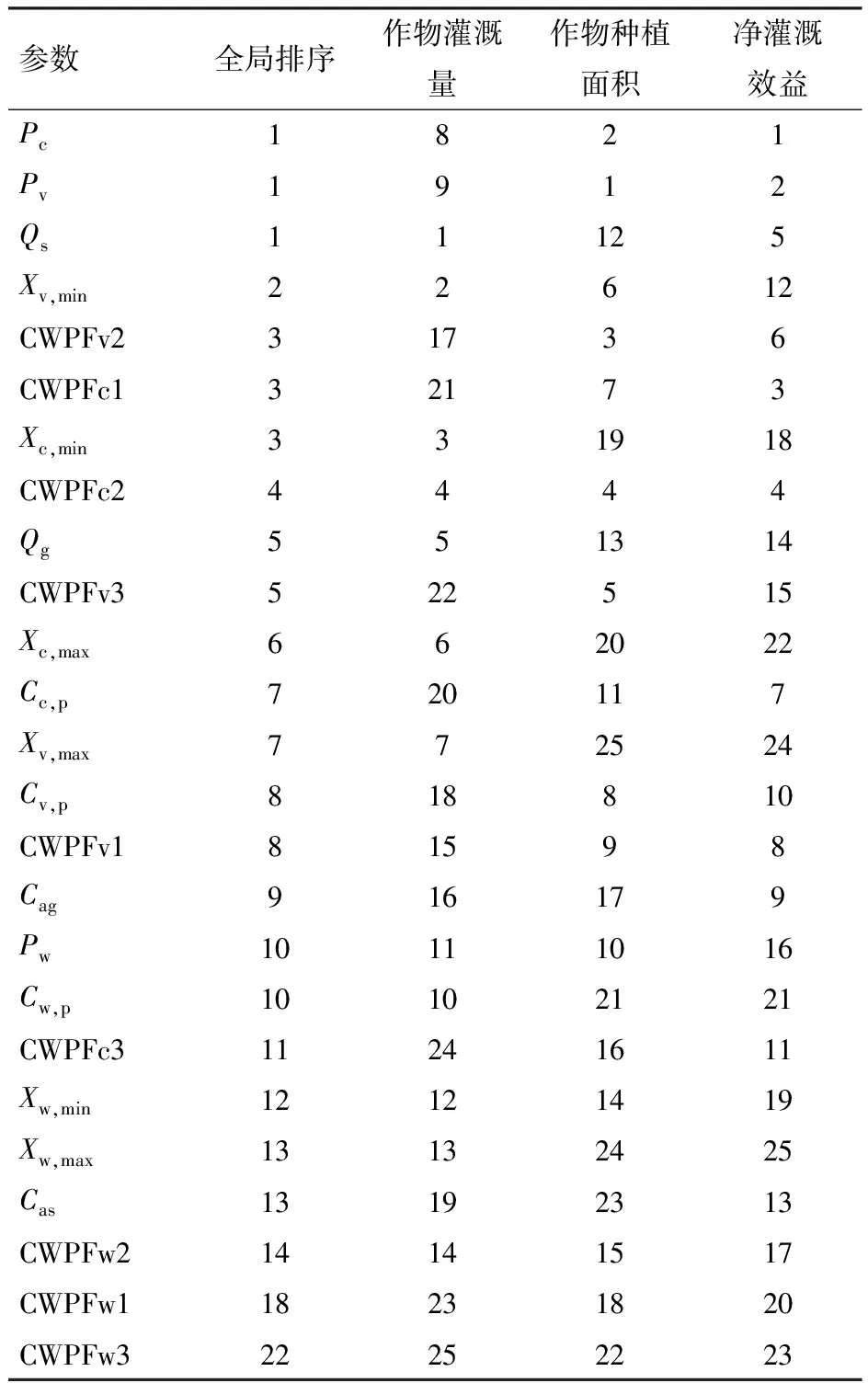
表3 参数敏感度排序
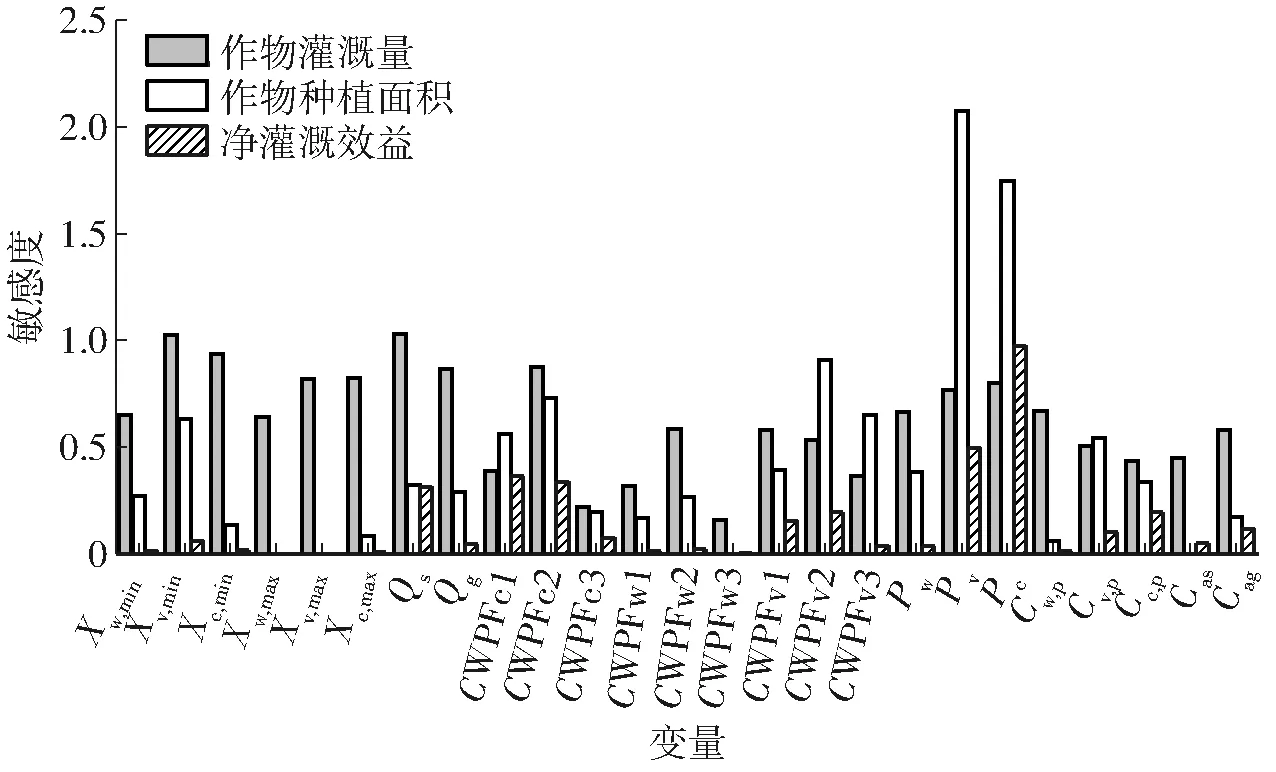
图4 不同输出变量的参数敏感度计算结果
2.3.1参数对决策变量的敏感性分析
以作物灌溉量X为输出变量时,其对总地表水灌溉量Qs和蔬菜最小灌溉量约束Xv,min最为敏感,敏感度超过了1.0,对总地下水灌溉量Qg和其他灌溉量约束(Xmin和Xmax)均有较强敏感性,敏感度多大于0.8(图4),这与实际情况相符合,即可用水量与灌溉量约束直接影响优化时作物灌溉量的分配。同时,作物价格P对X也有较大的影响,其敏感度为0.6~0.8,排序为8~11(图4和表3),表明在优化过程中作物价格会通过影响灌溉收益来影响灌溉量分配。相较上述参数,X对CWPF的敏感度总体较小,平均敏感度小于0.5(图4),排序主要在15以后(表3)。X对Cag的敏感性强于Cas,这可能是由于地下水价高于地表水价,地下水价波动对X的影响更大。总体上,X受模型输入参数的影响较大,很多输入参数对X的敏感度大于0.5。
以作物种植面积A为输出变量时,其对作物价格P,尤其是蔬菜和玉米的价格(Pv和Pc)非常敏感,敏感度大于1.0,其次对部分CWPF、作物种植成本Cp和最小灌溉量约束Xmin也呈较强敏感性(图4和表3)。对于同类参数,A对春小麦相关参数的敏感性较蔬菜和玉米的同类参数低(图4和表3),这可能是由于蔬菜和玉米的价格和产量较春小麦高,在优化中考虑到效益最大化的问题,蔬菜和玉米的种植面积分配优先于春小麦。总体上,A对CWPF、P、Cp和Xmin的敏感性明显大于其他参数,表明作物种植面积的分配与作物产量及其收益更密切。
2.3.2参数对目标值的敏感性分析
以目标值净灌溉效益G为输出变量时,其对玉米价格Pc呈极敏感,对Pv、Qs、CWPFc1和CWPFc2均呈较强敏感性,对地下水价格Cag、作物种植成本(Cc,p和Cv,p)、CWPFv1和CWPFv2呈一般敏感性。总体上,G对CPWF和价格相关参数都有不同程度的敏感性,这是由于作物产量和价格相关参数直接影响净灌溉效益。然而,相较于蔬菜和玉米,G对与春小麦有关的所有参数均不敏感,这是由于春小麦的产量在3种作物中最小且价格偏低,即其潜在灌溉收益最低,导致优化中春小麦对灌溉效益的影响最小,故其相关参数也最不敏感。另外,G对Qg不敏感,但对Qs呈敏感性,这是由于在优化中地表水灌溉量大约是地下水灌溉量的3倍,且地表水价较低,在优化中具有优先性,故地表水灌溉量的不确定性会对作物灌溉配水带来较大影响,进而影响净灌溉效益。
2.3.3参数敏感性全局分析
参数敏感度全局排序结果表明,玉米和蔬菜的价格(Pc和Pv)、总地表水灌溉量Qs为3个极敏感参数(表3中排序为1)。其中,Pc和Pv对X的影响较小,但对G和A的影响明显,而Qs对于X极敏感,但对于G和A较敏感,因此综合考虑参数对于不同输出变量的敏感性,上述3个参数均表现为极敏感。较敏感参数有7个,涵盖了最小灌溉量约束(Xv,min、Xc,min)、4种类型的CWPF以及总地下水灌溉量Qg(表3中排序为2~5)。一般敏感参数共有8个,包括各作物种植成本Cp、地下水价格Cag、玉米和蔬菜的Xmax以及春小麦价格Pw和1类CWPF(CWPFv1)(表3中排序为6~10)。总体上,作物价格、玉米和蔬菜的CWPF、总可用灌溉水量以及最小灌溉量约束的敏感性较强,其不确定性对优化模型的影响较大。
2.4 优化结果分析
根据参数敏感度全局排序,选取极敏感和较敏感参数(即全局排序1~5)作为优化模型的不确定性输入参数,包括部分作物价格(Pc和Pv)、部分CWPF(CWPFc1、CWPFc2、CWPFv2和CWPFv3)、部分灌溉量约束(Xv,min和Xc,min)以及总可用灌溉水量(Qs和Qg)共计10个参数,其他参数则不再考虑其不确定性,仍参照以往研究设置[23]。根据灌区实际情况,设置10个不确定性参数的变动范围,其中CWPF的变动范围仍参考图3,其他参数的变动范围如表4所示。对所选10个不确定性参数,在其变动范围内采用LH抽样法随机生成N个参数组(N≥20,每组包含10个参数),作为优化模型的不确定性参数输入,以此最终得到灌区用水的不确定性优化结果。
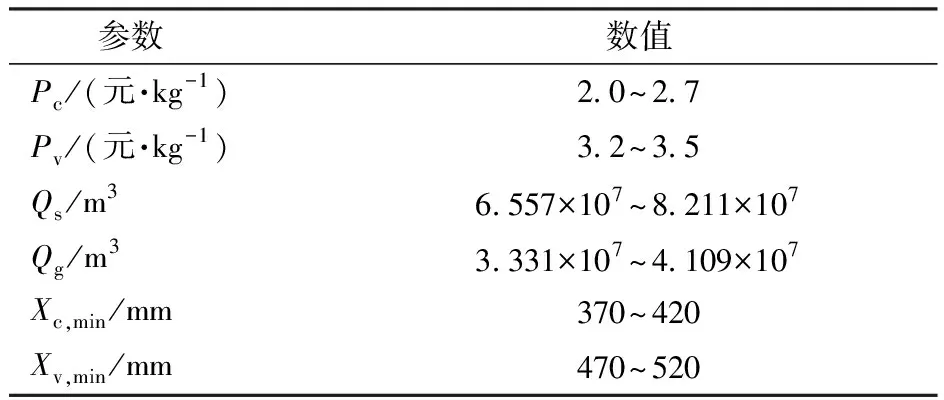
表4 优化模型敏感性参数变动范围
由图5可以看出,不同渠系之间的配水量存在明显空间差异,同时由于不确定性参数的影响,同一渠系的配水量也存在明显波动,如控制区Z4的地表水和地下水配水量分别为188.4~370.7 mm和32.2~221.8 mm,表现出较大的不确定性。同时,可注意到,地下水配水量的波动比地表水更明显,这可能是因为地下水水价较高,对灌溉效益影响更大,因此其价格的不确定性引起地下水配水量较大的波动。另外,部分渠系的地表水配水量波动很小,如FZ3、FZ4、FG1和FG2,这可能是这些渠系控制区的单方水效益较低,其配水量往往倾向分配最小值,受参数不确定性的影响较小。
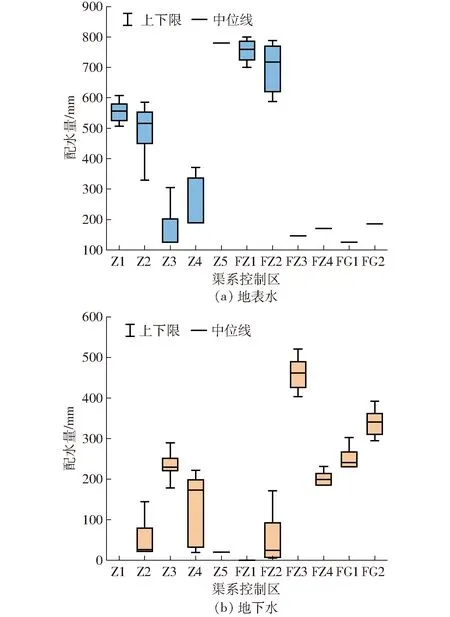
图5 各渠系控制区灌溉配水量优化结果
不同渠系控制区内各作物种植面积优化结果如图6(图中C、W和V分别表示玉米、春小麦和蔬菜)所示。从图6可以看出,各渠系控制区内玉米和蔬菜的种植面积比春小麦的种植面积波动更明显,这主要是由于春小麦产生的经济效益偏低,优化中种植面积往往会优先分配给玉米和蔬菜这些高效益作物,因此其受敏感参数不确定性的影响更大。同时,不同渠系间的作物种植面积分配及其波动也存在明显差异,这主要与控制区内作物-土壤单元分布有较大关系。
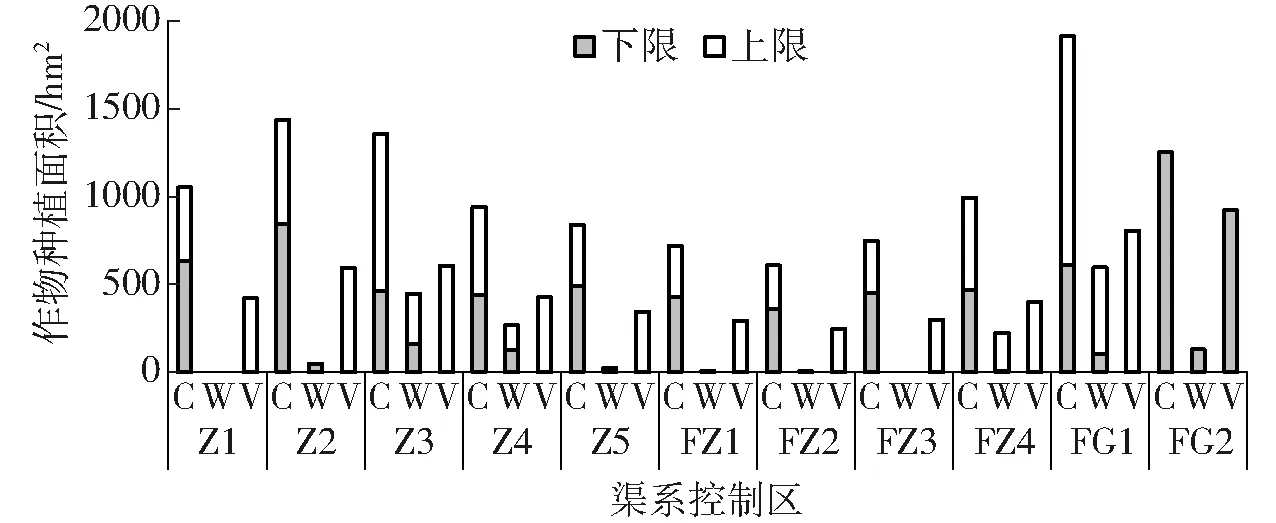
图6 各渠系控制区作物种植面积优化结果
图7为不同渠系内不同作物灌溉量的优化结果。由图7可知,各渠系之间作物灌溉量呈现出较大差异,如控制区Z1内的玉米灌溉量为57.0~69.3 mm,而控制区FZ4内的玉米灌溉量仅为40.0~44.2 mm。相比而言,玉米灌溉量的空间差异较蔬菜和春小麦明显,如春小麦灌溉量在许多渠系控制区几乎一致,这也与各作物的经济效益密切相关。由于不确定性参数的影响,各渠系内作物的灌溉量也表现出明显波动,但由于不同渠系内基本参数(如作物和土壤分布)等的差异,作物灌溉量的波动幅度在不同渠系之间呈现出较大不同,如控制区Z2内的蔬菜灌溉量为49.3~88.8 mm,呈现出较大不确定性,而一些渠系控制区内的蔬菜灌溉量波动为50 mm左右,春小麦的灌溉量几乎不变。
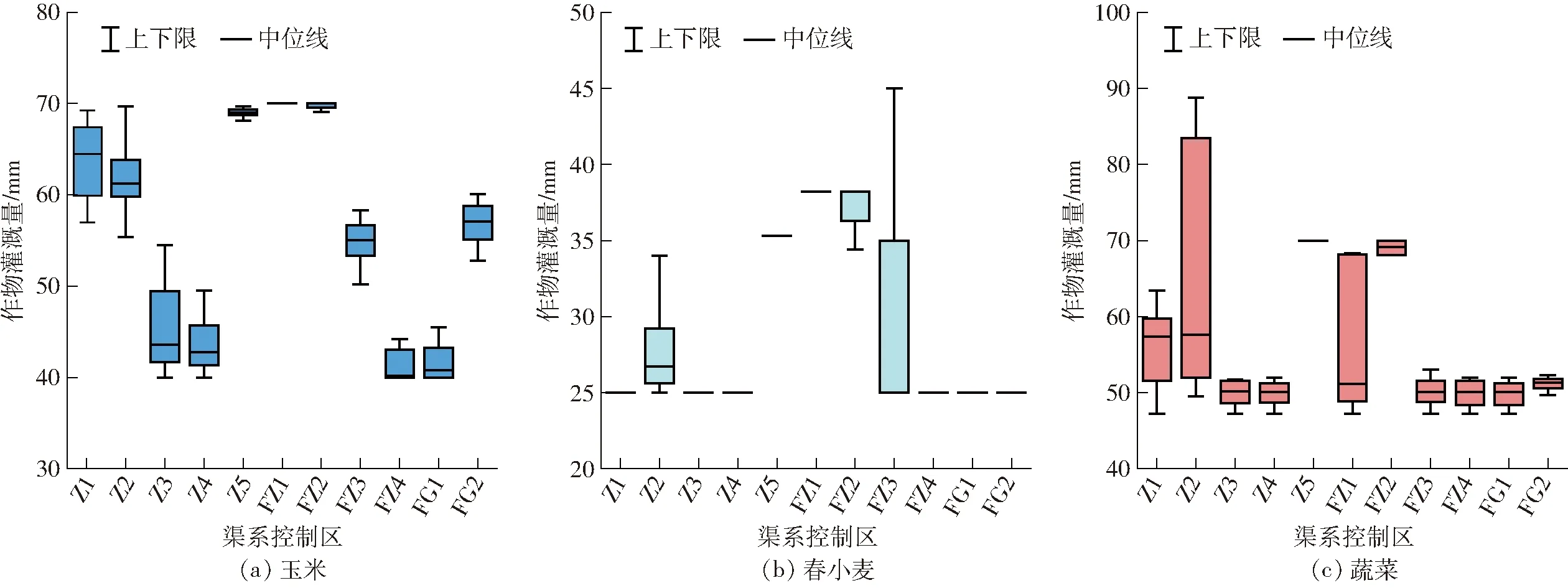
图7 各渠系控制区内各作物灌溉量优化结果
3 讨论
案例分析表明,本文所提出的基于LH-OAT的灌区用水优化模型敏感性分析与不确定性优化方法可以合理且高效地识别出高敏感性参数,并能够反映出多种敏感参数及其不确定性对优化结果的综合影响,是分析优化模型中不确定性参数全局敏感性的有效可行方法。其优势具体表现为:
(1)以往灌区水资源优化配置研究很少对模型中参数的敏感性进行定量分析,这不仅容易影响结果分析的准确性,而且在构建不确定性优化模型时,容易忽略部分敏感性参数的不确定性及其对优化结果的影响。本文将LH-OAT方法与灌区用水优化模型耦合,对优化模型中涉及的众多不确定性参数进行全局敏感性分析,以此获得各参数的敏感度排序,并筛选出高敏感参数作为不确定性参数输入,从而较全面地考虑了优化模型中的敏感性参数及其不确定性,且计算效率较高,具有实用性。
(2)相比以往灌区用水不确定性优化模型仅考虑某几个不确定性因素并予以量化表征,本文所提出方法可较全面地同时考虑多种敏感性参数的不确定性,通过这些参数的随机采样和组合,开展不确定性下的灌区用水优化。这种方式一方面不再需要分析不确定性参数的特征或分布规律来对其进行量化表征,从而降低了模型的复杂性,提高了优化计算的效率;另一方面优化结果能反映众多敏感性参数的综合影响,而不仅仅是某一因素的单一影响。
4 结论
(1)针对灌区水资源优化配置过程中存在众多不确定性参数而影响模型效率的问题,将LH-OAT方法与灌区用水优化模型耦合,构建了基于LH-OAT方法的灌区用水优化模型参数敏感性分析与不确定性优化方法。将该方法应用于黑河流域中游盈科灌区的灌溉用水优化中,分别以优化模型的目标值——净灌溉效益G和决策变量——作物灌溉量X和作物种植面积A为输出变量,以6类共25个不确定性参数为输入变量,定量确定了各参数针对不同输出变量的敏感度及其全局排序,筛选出10个高敏感性参数,并将高敏感参数作为模型不确定性参数输入,获得了不确定性下的灌区用水优化结果。
(2)各参数对不同输出变量的敏感性存在差异,综合考虑各输出变量,极敏感参数为玉米和蔬菜的价格及总地表水灌溉量,较敏感参数涉及蔬菜、玉米最小灌溉量约束、4种类型的作物水分生产函数以及总地下水灌溉量,合理反映出不确定性参数对优化结果的综合影响。
(3)基于高敏感性参数的灌区用水不确定性优化高效可行,较全面地考虑了高敏感的不确定性参数,从而大大降低不确定性下优化模型结构和求解的复杂性,提高模型效率,并且能综合考虑多种不确定性参数对优化结果的影响,为灌区水资源优化配置研究提供了实用且有效的方法参考。

