围岩和衬砌劣化作用下隧道底部结构动力响应
王景春 常子红 王大鹏 刘凯林
1.石家庄铁道大学 安全工程与应急管理学院, 石家庄 050043; 2.石家庄铁道大学 土木工程学院, 石家庄 050043
随着我国高速铁路事业的快速发展,投入运营的铁路隧道越来越多。在列车荷载及外界环境作用下隧道安全性会降低。一方面,混凝土碳化、钢筋锈蚀等因素会造成混凝土强度降低、衬砌开裂、渗漏水等;另一方面,基底围岩性能劣化会引起隧道结构开裂、破损等。为准确掌握列车振动荷载作用下隧道结构服役性能,需要考虑衬砌和围岩劣化对隧道结构的影响。
国内外学者针对隧道衬砌及围岩劣化问题进行了持续探索。刘昌等[1]通过建立衬砌劣化特性的时效解析模型,得到衬砌劣化系数越大,支护时间越晚,支护反力终值越小,围岩变形终值越大。Xu等[2]利用模型试验分析了冻融循环寒区隧道衬砌结构劣化规律,得出衬砌劣化会导致衬砌结构裂缝逐渐发展,衬砌结构严重开裂。曾冬艳等[3]研究了岩石轻微劣化、中等劣化及严重劣化3种情形下围岩变形情况。刘四进等[4]通过数值模拟分析了管片衬砌结构劣化规律。
既有文献对衬砌和围岩劣化作用下隧道衬砌结构力学性能、变形规律和劣化机理进行了研究,但未考虑劣化作用对隧道结构动力响应的影响。本文采用数值模拟方法,在轨道板上直接施加拟合的列车荷载,着重分析衬砌和围岩劣化作用下隧道底部结构动力响应特性,为高速铁路隧道养护及加固提供参考。
1 衬砌和围岩劣化特性分析
1.1 衬砌劣化特性
衬砌混凝土力学性能随着服役时间发生改变。山岭隧道所处环境为一般大气环境,故采用牛荻涛等[5]提出的一般大气环境下混凝土时变模型,描述混凝土力学性能随着服役时间增长而退化的过程。即
式中:μ(t)、σ(t)分别为t时刻混凝土抗压强度平均值和标准差;μ0(t)、σ0(t)分别为混凝土28 d龄期抗压强度平均值和标准差。
依据GB 50010—2011《混凝土结构设计规范》中的C15—C80混凝土抗压强度标准值和弹性模量,拟合得到混凝土弹性模量与抗压强度标准值的关系,即
式中:Et、fck,t分别为服役t年时混凝土的弹性模量和抗压强度标准值。
二次衬砌常采用C30混凝土,其抗压强度平均值和变异系数分别取20.1 MPa和0.11。代入式(1)可得不同服役时间混凝土抗压强度,将其代入式(3)计算得到C30混凝土不同服役时间的弹性模量,见表1。
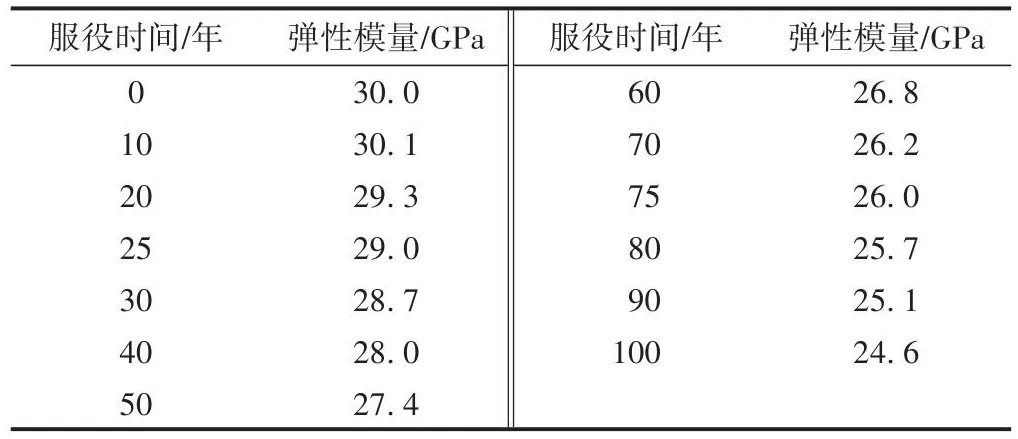
表1 C30混凝土不同服役时间的弹性模量
1.2 围岩劣化特性
为了分析围岩劣化作用下隧道结构动力响应特性,通过改变围岩力学参数模拟围岩劣化。岩石进入屈服阶段后,内部微裂纹累积、扩展产生损伤,岩体颗粒间黏结强度不断减小;微裂纹累积到一定程度产生宏观裂纹,岩体发生破坏。因此可以认为随着围岩不断劣化,其弹性模量和黏聚力逐渐降低。对于软弱破碎岩体,内摩擦角会随塑性应变增大而增大。
TB 10003—2016《铁路隧道设计规范》中Ⅴ级围岩的力学性能指标取值范围:弹性模量为1 ~ 2 GPa,黏聚力为0.05 ~ 0.20 MPa,内摩擦角为20° ~ 27°。假定在环境作用下围岩均匀劣化,计算得到运营期内不同服役时间Ⅴ级围岩力学性能指标,见表2。
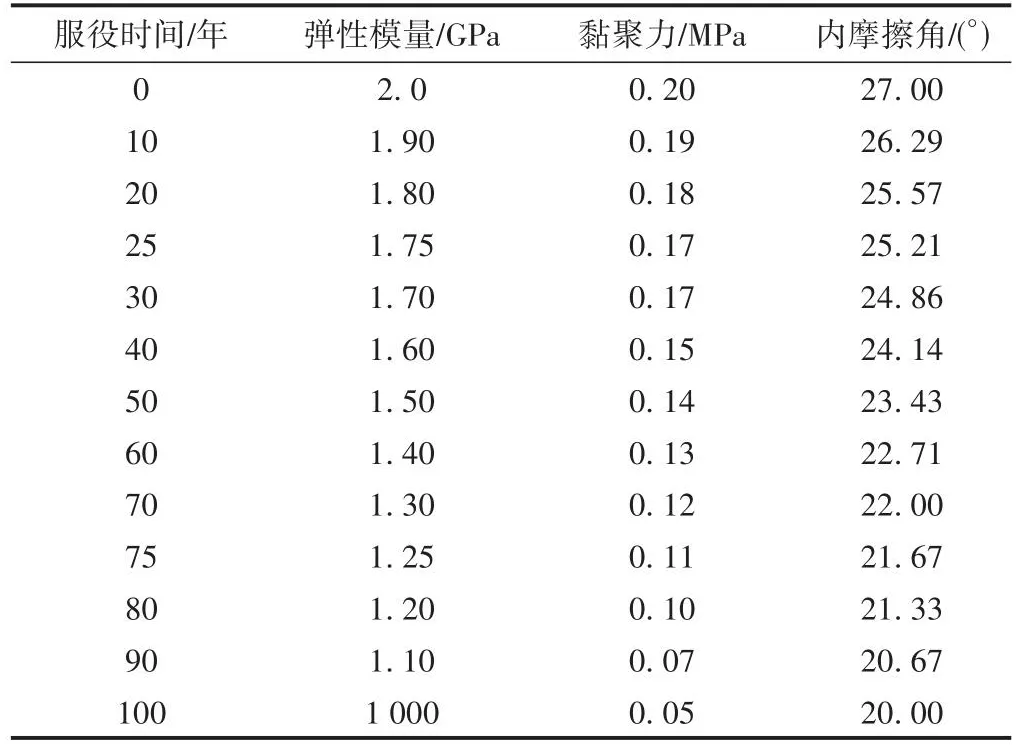
表2 不同服役时间Ⅴ级围岩力学性能指标
2 隧道结构动力响应特性数值模拟
2.1 列车振动荷载模拟
采用人工激励的方式来模拟列车振动荷载。采用文献[6]中修正后的列车振动荷载表达式计算列车振动荷载对轨道产生的横向和竖向激振力。修正后的列车荷载F(t)为
式中:k1、k2分别为相邻轮轨力叠加系数、刚轨分散系数,k1= 1.5,k2= 0.7;P0为车辆静载;P1、P2、P3分别为行车不平顺、动力附加荷载和波形磨耗引起的振动荷载。
以高速列车CRH3为例进行模拟,列车运行速度350 km/h,轴向荷载170 kN。
2.2 模型建立与参数确定
计算断面采用TB 10621—2014《高速铁路设计规范》中Ⅴ级围岩高速铁路双线隧道标准断面,计算模型尺寸为100 m(长) × 40 m(宽) × 120 m(高),见图1。围岩采用摩尔库伦模型,衬砌及轨道板采用弹性模型。依据GB 50086—2001《铁路隧道围岩分级标准》确定围岩及隧道结构的力学参数,见表3。
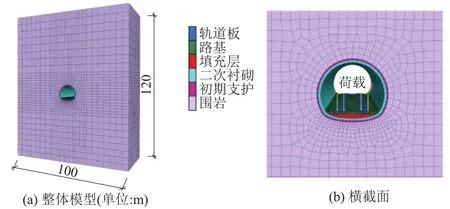
图1 计算模型
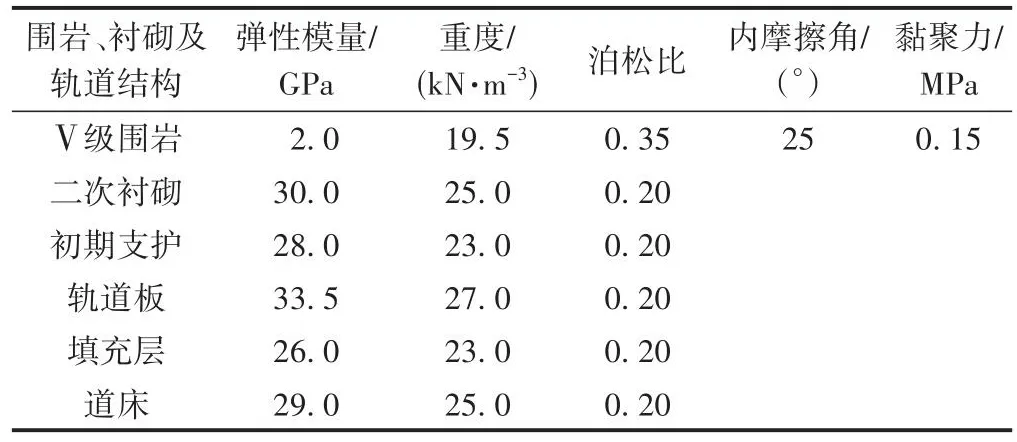
表3 计算参数
2.3 边界条件及阻尼
为消除振动波在边界上产生的反射,在模型侧面及底部设置黏弹性边界。分析动力响应时采用Rayleigh阻尼来减弱结构体系在自然振动模式下的振幅。阻尼矩阵C的计算式为
式中:M、K分别为质量矩阵和刚度矩阵;α、β分别为质量阻尼系数和刚度阻尼系数。
3 计算结果与分析
分三种工况对列车通过时隧道结构动力响应进行分析。工况1—工况3分别为不考虑劣化作用、考虑衬砌劣化作用和考虑围岩劣化作用。
在隧道衬砌结构拱顶、边墙、边墙与仰拱连接处、左侧仰拱底部、仰拱中心布置测点,如图2所示。
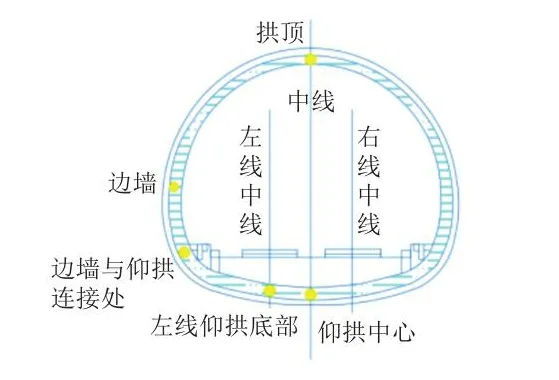
图2 测点布置
3.1 不考虑劣化作用时隧道结构动力响应
工况1隧道结构竖向位移和振动加速度时程曲线见图3。
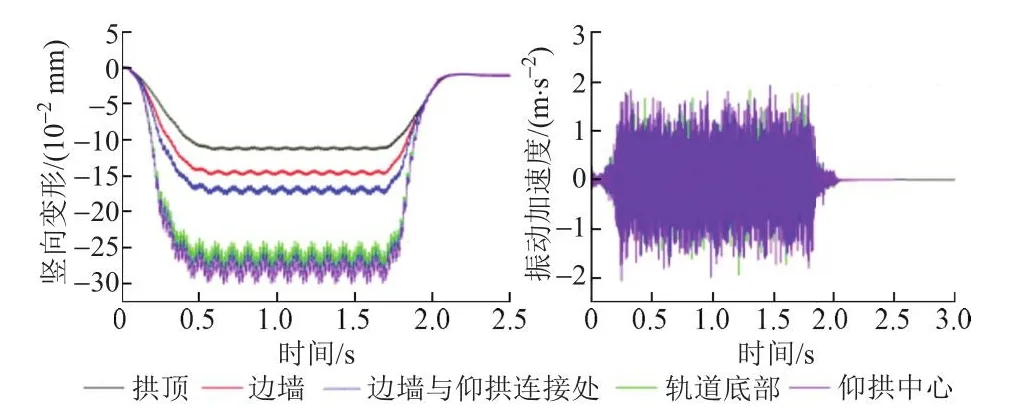
图3 工况1隧道结构竖向位移和加速度时程曲线
由图3可知:工况1仰拱中心测点竖向位移及振动加速度比其他测点大。因此,选择仰拱中心为研究对象,结合表1和表2,进一步分析衬砌及围岩劣化作用下列车通过时隧道底部结构动力响应。
3.2 考虑衬砌劣化作用时隧道底部结构动力响应
1)竖向位移及加速度
工况2仰拱中心测点竖向位移及振动加速度最大值随服役时间变化曲线见图4。可知:①考虑衬砌劣化作用时,从开始服役到服役100年仰拱中心竖向位移最大值变化不明显,稳定在0.030 ~ 0.033 mm;②仰拱中心振动加速度最大值随服役时间延长先减小后增大。

图4 工况2仰拱中心测点竖向位移及振动加速度最大值随服役时间变化曲线
2)动应力
工况2仰拱中心测点动应力最大值随服役时间变化曲线见图5。可知:①仰拱中心测点动拉应力最大值和动压应力最大值均随服役时间增大而减小;从开始服役到服役100年仰拱中心测点动拉应力最大值从0.813 MPa降至0.732 MPa,降幅9.96%;②动压应力最大值从2.752 MPa降至2.311 MPa,降幅16.02%。
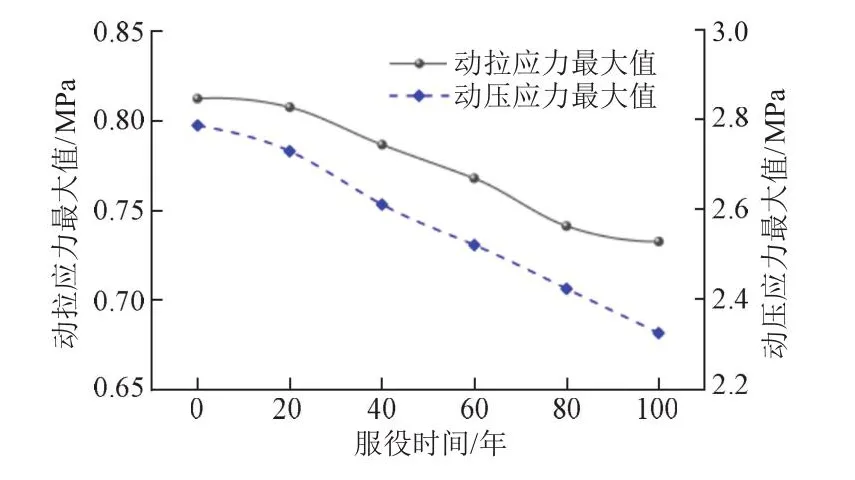
图5 工况2仰拱中心测点动应力最大值随服役时间变化曲线
3.3 考虑围岩劣化作用时隧道底部结构动力响应
1)竖向位移及加速度
工况3仰拱中心测点竖向位移及振动加速度最大值随服役时间变化曲线见图6。可知:①考虑围岩劣化作用时,仰拱中心测点竖向位移基本上随服役时间延长而增大,从开始服役到服役100年竖向位移由0.030 mm增至0.045 mm,增幅50%;②仰拱中心测点振动加速度随服役时间延长先增大后减小,可见围岩劣化对隧道底部振动加速度影响较大。
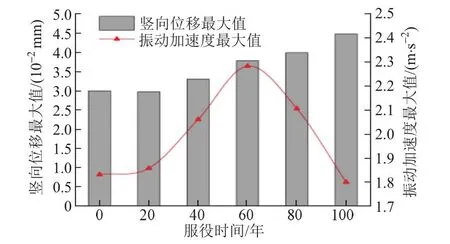
图6 工况3仰拱中心测点竖向位移及振动加速度最大值随服役时间变化曲线
2)动应力
工况3仰拱中心测点动应力最大值随服役时间变化曲线见图7。可知:①仰拱中心测点动压应力随服役时间延长而增大,从开始服役至服役100年动压应力由2.752 MPa增至5.139 MPa,增幅86.7%。②动拉应力随服役时间延长先减小后增大,从服役60年左右开始增大。混凝土抗拉性能差,动拉应力增大对隧道底部结构非常不利。结合图6中加速度变化规律可知,服役60年左右隧道底部动力响应变化明显,因此隧道服役后期应加强隧道底部及周围岩体的监测与病害防治。
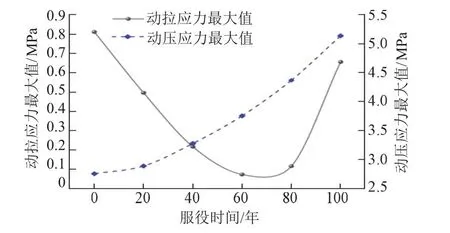
图7 工况3仰拱中心测点动应力最大值随服役时间变化曲线
4 结论
本文通过数值模拟分析了不考虑与考虑衬砌及围岩劣化作用时隧道结构动力响应。主要结论如下:
1)从整体来看,衬砌劣化对隧道底部结构动力响应影响较小。考虑衬砌劣化作用时,从开始服役到服役100年,隧道底部结构竖向位移基本保持不变,振动加速度先减小后增大,动应力逐渐减小。
2)围岩劣化对隧道底部结构动力响应影响明显。从开始服役至服役100年,隧道底部竖向位移增加50.0%,动压应力增大86.7%,动拉应力先减小后增大。服役60年左右,隧道底部结构振动加速度变化显著,动拉应力急剧增大,拉应力增加对隧道底部结构极为不利。加之竖向位移持续增大,隧道服役后期应加强隧道底部及周围岩体的监测与病害防治。

