基于代理模型的400 km/h高速铁路车-桥系统关键参数优化方法

张可新 同新星 李克冰 杨勃

1.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心， 北京 100081； 2.西安理工大学 机械与精密仪器工程学院，西安 710048； 3.中国铁道科学研究院集团有限公司 铁道建筑研究所， 北京 100081

高速铁路对行车安全性和乘坐舒适性提出了极高要求。我国高速铁路大量使用桥梁以减少工后沉降和轨道不平顺性［1-2］。简支梁因其结构简单、施工方便、成本低等优点，被广泛地应用于我国高速铁路建设中。预应力混凝土简支梁长期受预应力的压缩作用，随着时间的推移会产生徐变压缩效应［3］。因其下端压缩变形高于上端，导致简支梁出现徐变上拱现象，从而造成高速铁路线路纵断面的不平顺性，影响高速铁路的行车安全性和乘坐舒适性［4-5］。车-线-桥耦合系统研究表明［6-7］：列车轴重与桥梁徐变上拱是影响列车垂向加速度的重要因素。因此，在桥梁密集的高速铁路设计阶段，确定合理的列车轴重和桥梁徐变上拱值对高速铁路的安全性和舒适性设计具有重要意义。

关于高速铁路桥梁徐变上拱对列车动力学响应的研究主要集中于桥梁徐变上拱的仿真［8-9］、徐变上拱对列车的动力学响应分析、徐变上拱限值研究等方面。勾红叶等［10］以桥梁下沉、徐变上拱值为研究对象，通过车体垂向加速度和轮轨垂向力评价行车安全，构建桥梁变形映射通用模型，并运用仿真分析与数据拟合的方法研究高速铁路桥梁附加变形与行车安全的动态关系模型。杨宏印等［11］推导了考虑轨道不平顺和轮轨脱离的车轮-轨道-桥梁耦合动力方程，使用有限元方法分析桥梁徐变上拱值对系统的加速度、轮轨接触力的响应规律。徐庆元等［12］利用ANSYS软件建立高速列车-纵连板式无砟轨道-桥梁耦合动力学模型，研究徐变上拱值对车体最大加速度、最大轮轨力等的影响。黎国清等［13］通过实车试验研究了徐变上拱引起的轨道不平顺性，构建车-桥系统动力模型，分析桥上轨道不平顺幅值对垂向加速度的影响规律。柏华军［14］以温差效应下的墩顶竖向变形为对象，基于车-桥耦合分析软件，研究温度效应对车-桥系统动力响应的影响规律。田新宇等［15］运用MIDAS/Civil软件建立车辆-轨道-桥梁耦合动力学模型，分析徐变上拱值对车体垂向加速度、舒适度等的影响，获得桥梁残余徐变上拱的设计限值。

目前，我国已自主化全面构建了时速350 km成套技术体系，并在京沪高铁、郑徐高铁开展综合试验，探索了时速380 ~ 420 km高速铁路的相关技术问题，具备向时速400 km发展的潜力。时速400 km高速铁路技术参数尚未完全确定，同时动车组技术参数与基础设施设计参数存在一定的耦合关系，因此需要进一步完善系统正向设计和匹配优化方法，从而合理地制定新一代更高速、更安全、更舒适的高速铁路设计参数。本文以列车垂向加速度为目标，基于代理模型和优化设计理论，研究时速400 km高速铁路车-桥系统关键参数优化设计方法，为桥梁徐变上拱控制及车辆设计提供参考。

1 高速列车垂向加速度代理模型构建

桥梁徐变上拱和列车轴重是影响列车垂向加速度的关键参数，且两个参数相互影响，关系比较复杂，难以获得精确的解析表达式。基于有限样本数据的代理模型能够以极高的精度描述参数之间的关系，为研究车-桥系统关键参数优化提供了有效途径。

1.1 基于拉丁方的设计变量抽样

拉丁超立方抽样（Latin Hypercube Sampling，LHS）是一种从多元参数分布中近似随机抽样的方法，能在较少抽样的情况下获得较高的计算精度。在350 km/h高速铁路技术基础上，以列车轴重和桥梁徐变上拱值为设计变量，其取值范围分别设定为［12，17］t和［3，13］mm。基于LHS方法抽样获得的列车轴重和徐变上拱值的组合数据，得到25组不同的设计变量组合（表1），可为车辆垂向加速度的虚拟仿真提供有效输入参数组合。

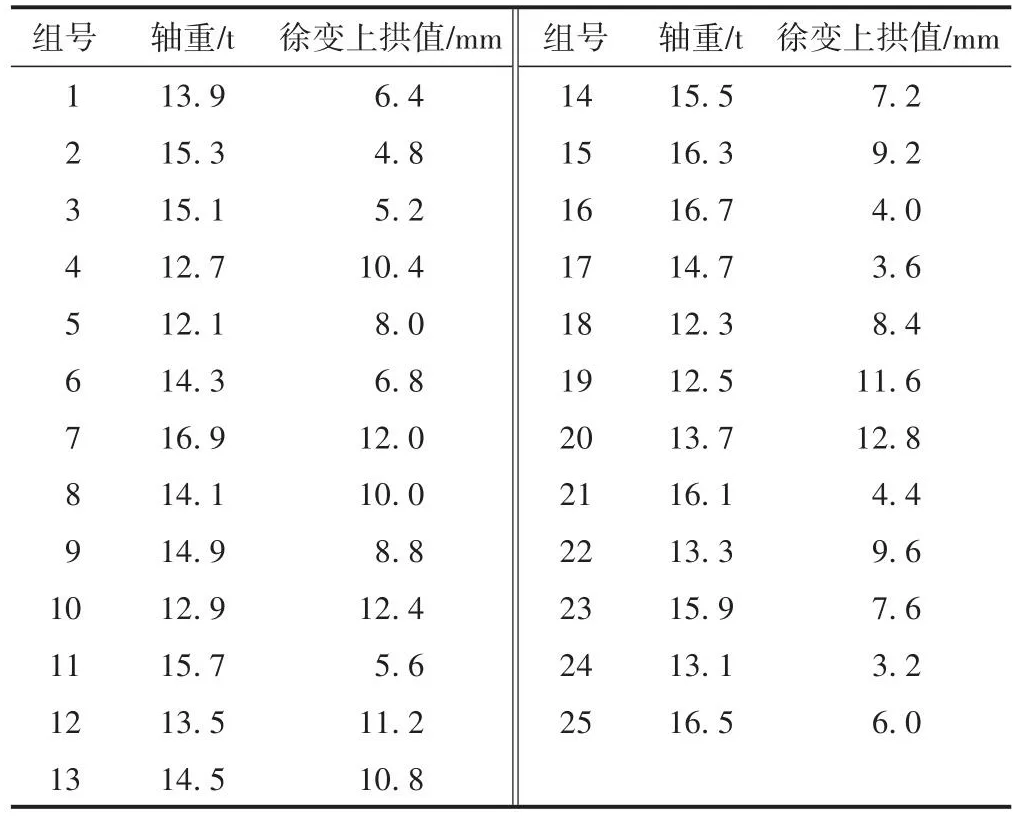
表1 基于LHS方法抽样获得的列车轴重与徐变上拱值的组合数据

1.2 高速列车垂向加速度虚拟仿真

通过构建高速铁路车-桥系统动力学模型研究列车垂向动力学特性是有效的分析方法。本文考虑CRH380B列车结构特征，以连续32 m混凝土简支梁为对象，基于LSH方法抽样的输入参数组合，通过构建三维车桥耦合动力分析模型，研究400 km/h高速铁路不同列车轴重和桥梁徐变上拱值组合下的高速列车垂向加速度，为构建其代理模型提供合理有效的样本数据。

1.2.1 车-桥系统动力分析模型及求解方法

三维车-桥动力耦合系统由车辆子系统和桥梁子系统两部分组成，子系统之间通过给定的轮轨相互作用模型相联系，系统的内部自激励包括轨道不平顺、车辆蛇行运动等。

轮轨间相互动力作用，横向采用轮轨切向蠕滑假定的线性简化假定，竖向采用轮轨垂向密贴假定。分别建立车辆子系统、桥梁子系统的动力方程，联立车辆子系统方程和桥梁子系统方程，可得到车-桥系统的动力方程，即

式中：Mv、Cv、Kv、Xv分别为单节车辆的质量矩阵、阻尼矩阵、刚度矩阵、位移向量；Cc为轮轨间蠕滑产生的附加阻尼矩阵；Fv为作用在单节车辆上的外加力向量；Mb、Kb分别为桥梁子系统的质量矩阵和刚度矩阵；Cb为桥梁子系统的阻尼矩阵；Xb为桥梁子系统的位移向量；Fb为作用在桥梁子系统的力向量，即轮轨间作用力。

系统方程的建立方法及各矩阵向量参见文献［16-17］，系统方程的求解采用全过程迭代法［18］。首先假定桥梁子系统为刚性，求解独立的车辆子系统方程，得到列车轮轨间作用力时程，然后将轮轨间作用力施加于桥梁，求解独立的桥梁动力方程得到桥梁的动力响应。将求出的桥面动力响应时程与轨道不平顺叠加作为新的车辆系统激励进行下一步迭代。

1.2.2 不同抽样的车辆垂向加速度计算

以CRH380B动车组为对象，采用中国高速铁路无砟轨道不平顺谱转换的时域不平顺样本作为动车组的轨道不平顺激励。基于LSH方法抽样的徐变上拱和轴重参数组合，通过求解三维车桥耦合动力学模型，获得400 km/h高速铁路列车轴重和徐变上拱值不同组合的车辆垂向加速度，为构建车体垂向加速度代理模型提供了有效的样本数据。基于三维车-桥模型获得的不同列车轴重与徐变上拱值组合的车辆垂向加速度见表2。

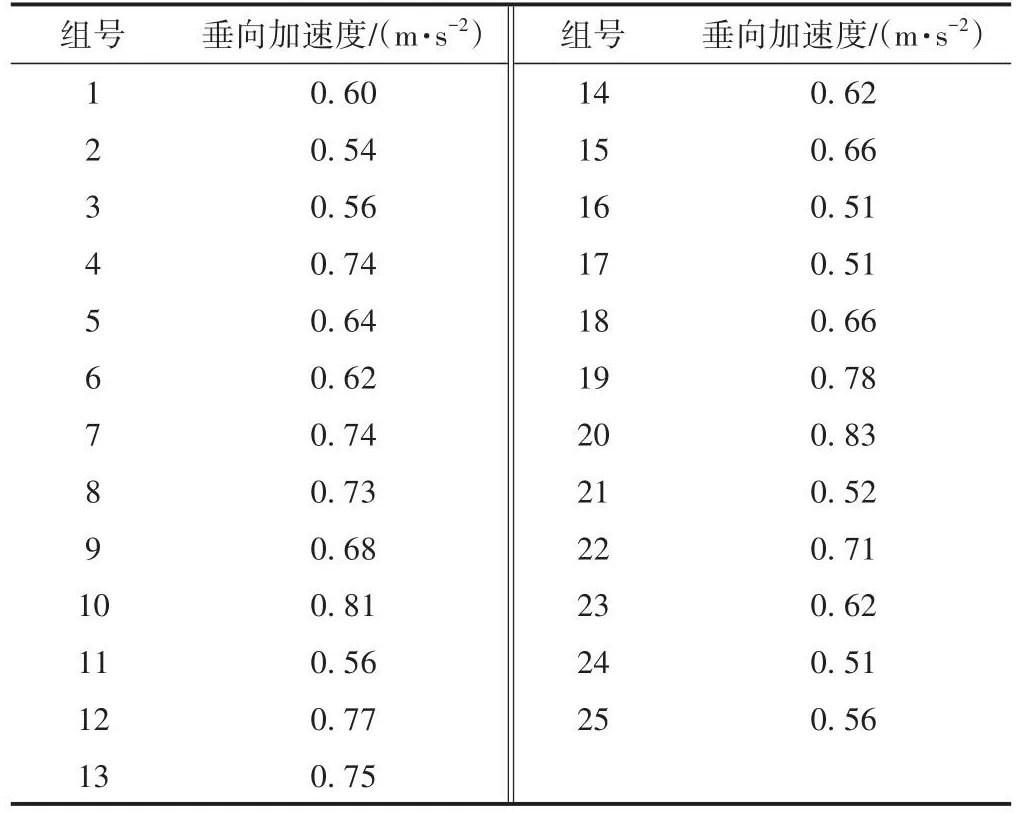
表2 基于三维车-桥模型获得的不同列车轴重与徐变上拱值组合的车辆垂向加速度

1.3 基于Kriging的车体垂向加速度代理模型

1.3.1 Kriging代理模型构建方法

Kriging模型是一种基于随机过程的统计预测法，具有在样本点上精确插值和预测的优点，对于强非线性问题具有良好的拟合能力。假设x∈ Rd为多维输入向量，y（x）为输出响应，则Kriging模型的表达式为

式中：p为多项式的项数；βi为回归系数；Z（x）表示一个满足正态分布N（0，σ2）的高斯随机过程，均值为0；fi（x）为第i个多项式。

Z（x）的协方差为

式中：cov（·）为协方差函数；σ2为方差；R（·）为相关函数；θ为相关系数向量；xi和xj分别为第i和j个输入设计变量。

本文选取的常数回归项和高斯相关函数为

式中：d为设计变量的维数；θk为输入变量的第k个分量的相关性系数；xi，k和xj，k分别表示第i和j个输入设计变量矢量的第k维分量。

输出y（x）的最优线性无偏估计为

式中：y为样本响应值向量̂为β的最大似然估计；R为相关函数矩阵；r为相关函数向量；f为长度为n的单位列向量。

表达式为

σ2的估计为

与σ̂2都是式（3）相关系数向量θ的函数，θ的值可通过求解下式得到。

式中：Φ（·）为极大似然估计函数。

通过模式搜索算法求解无约束优化问题式（8），可得相关系数向量θ；将其代入式（2）—式（4），构建得到Kriging代理模型。

1.3.2 基于Kriging的代理模型构建

以高速列车轴重、桥梁徐变上拱值为设计变量，首先通过求解三维车桥耦合模型获得列车以400 km/h速度通过桥梁时的一系列车体垂向加速度的数据样本；然后基于Kriging代理模型构建原理，建立列车轴重、桥梁徐变上拱值与车体垂向加速度的代理模型。归一化后的响应曲面如图1所示。可知：①车体垂向加速度与列车轴重、桥梁徐变上拱值成非线性的关系，其响应曲面光滑平顺。列车轴重越大，且桥梁徐变上拱值越小，则高速列车的车体垂向加速度越小。②车体垂向加速度对徐变上拱值的敏感性远远高于对车辆轴重的敏感性，应在系统设计中限制桥梁的徐变上拱限值。另外，构建的代理模型响应面与通过车-桥动力学模型计算的结果（表2）趋势一致，充分说明了代理模型的有效性。

图1 基于Kriging方法构建的车体垂向加速度代理模型归一化后的响应曲面

1.3.3 代理模型精度分析

基于Kriging方法构建的列车车体垂向加速度代理模型的评价参数见表3。可知，代理模型预测精度达到了98.96%，复相关系数达到了0.995 3，表明代理模型具有较高的精度，能够精确描述高速列车轴重、桥梁徐变上拱值与车体垂向加速度的非线性关系。此外，轴重和桥梁徐变上拱值的参数向量分别为0.316 4和0.499 3，证明了徐变上拱值的变化对车体垂向加速度影响更大，与响应面呈现的规律一致。

表3 基于Kriging的高速列车车体垂向加速度代理模型评价参数及其精度

2 基于代理模型的车-桥系统关键参数优化

2.1 高速列车垂向加速度优化模型

为了在400 km/h高速铁路系统设计阶段为桥梁及列车设计提供依据，以400 km/h高速铁路为对象，利用车体垂向加速度评价安全性和舒适性。在满足TB 10621—2014《高速铁路设计规范》的约束条件下，以列车轴重与桥梁徐变上拱值为设计变量，以车体垂向加速度最小为设计目标，构建基于代理模型的400 km/h高速铁路车-桥系数关键参数优化模型，即

式中：x1和x2为设计变量，分别代表高速铁路列车的轴重和桥梁的徐变上拱值；f（x1，x2）是基于代理模型构建的高速列车车体垂向加速度函数。

2.2 基于布谷鸟搜索算法的优化模型求解

布谷鸟搜索算法（Cuckoo Search Algorithm，CSA）是一种新型进化类全局优化算法，其思想借鉴了自然界中布谷鸟寻窝产卵的巢寄生繁殖方式和莱维飞行原理。因调试参数少、全局寻优能力强、鲁棒性好且无须重新匹配调试参数等优点，CSA被广泛地应用到工程优化领域。CSA算法第t+1代第i个布谷鸟的局部随机游走位置更新表达式为

式中：xti+1、xti分别为第t+1代、第t代的第i个布谷鸟位置；α>0为步长比例因子；s为步长；⊗代表向量点乘；H（u）为Heaviside函数；pa为外来鸟蛋被巢主鸟发现的概率，pa∈[0，1]；ε为随机数；xtj和xtk代表不同的随机序列。

基于莱维飞行原理，全局随机游走的位置更新表达式为

式中：λ为莱维指数；L（s，λ）为莱维飞行函数；Γ（λ）为λ函数。

基于CSA算法的高速铁路车-桥系统关键参数优化流程见图2。

图2 基于CSA算法高速铁路车-桥系统关键参数优化流程

具体步骤如下：

1）分别设定车辆轴重（x1）和桥梁徐变上拱值（x2）的变化范围，给定种群数量、发现概率和最大迭代代数，预先设定最大允许优化代数（Tmax）。

2）基于拉丁方抽样原理，以车辆轴重和徐变上拱值为设计变量，在其变化区间内进行有限抽样。

3）构建三维车-桥系统动力学模型，基于步骤2）中的输入参数，分别计算得到不同组合的车体垂向加速度，为代理模型提供有效的设计样本。

4）采用Kriging方法，基于步骤3）中的样本点构建车体垂向加速度与车辆轴重和桥梁徐变上拱值的代理模型f（x1，x2）。

5）基于步骤4）中的代理模型，以车辆轴重和桥梁徐变上拱值为设计变量，构建以车体垂向加速度最小为目标的高速铁路车-桥系统关键参数优化模型。

6）通过丢弃适应度较差的鸟窝和选取适应度较好的鸟窝，生成新的第t代种群。

7）采用局部和全局随机游走更新公式对第t代种群设计变量xi进行更新，并计算每个鸟窝的适应度函数值。

8）对终止条件进行判断，如若满足t>Tmax，则输出优化结果；否则，令迭代次数t=t+1并返回步骤6）。

2.3 计算结果分析

采用布谷鸟搜索算法对构建的高速铁路车-桥系统关键参数的优化模型进行优化求解。设定布谷鸟搜索算法的鸟窝数为20个，发现概率为0.25，随机生成初始设计变量，迭代优化次数调试后设为100。基于布谷鸟搜索算法的高速铁路车-桥系统关键参数优化迭代过程见图3。可知，车体垂向加速度目标函数值随着迭代次数的增加逐渐趋于稳定，在第100代时收敛于0.490 9 m/s2，远小于TB 10621—2014的容许值（1.3 m/s2），表明车体垂向加速度能够满足高速铁路运行安全性和舒适性的要求。此时x1= 15 t，x2= 3 mm。通过代理模型和优化理论获得的设计变量最优值处于可行区域的边界，这与目标函数的性质相吻合。说明本文提出的方法对优化高速铁路车-桥系统关键参数快速有效。

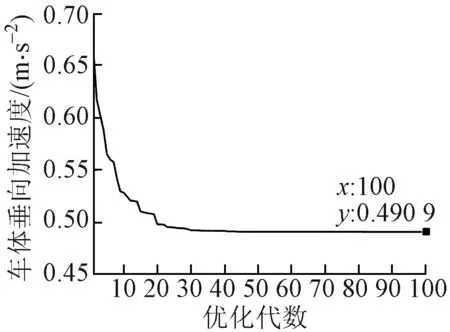
图3 基于布谷鸟搜索算法的高速铁路列车垂向加速度优化迭代过程

3 结论

针对高速铁路车-桥系统建模复杂难以优化的问题，本文以最小车体垂向加速度为目标，基于代理模型和优化设计理论，研究高速铁路车-桥系统关键参数优化方法，得到结论如下。

1）在构建的400 km/h高速铁路三维车-桥系统动力学模型的基础上，基于拉丁方抽样和仿真分析，建立了车体垂向加速度的Kriging代理模型，其精度达到了98.96%，复相关系数达到了0.995 3，可有效描述车体垂向加速度与列车轴重、桥梁徐变上拱值的相互关系。

2）提出了一种基于代理模型的时速400 km高速铁路车-桥系统关键参数优化方法，基于代理模型和优化理论获得了最优列车轴重和桥梁徐变上拱值，分别为15 t和3 mm，此时车体垂向加速度最小，其值为0.490 9 m/s2，小于TB 10621—2014容许值（1.3 m/s2），验证了本文方法的正确性和有效性。