基于多周期趋势分解和两级融合策略的浪高预测方法

郑小罗，李其超，姜 浩，宋 巍*，邓小东

（1. 上海海洋大学 信息学院，上海 201306；2. 国家海洋局 东海预报中心，上海 200081）

浪高是全球大气系统中的一个重要参数，由于海洋环境极其复杂，预测浪高是一项非常具有挑战性的任务[1]。一般地，浪高的预测方法大致可以分为3 类：数值波浪模型、经典线性时间序列模型和机器学习模型。

数值波浪模型基于能量平衡方程，例如第三代波浪模型WAM（Wave Model）、基于WAM 的近岸波浪模拟SWAN（Simulating Waves Nearshore）和WW3（WAVE WATCH Ⅲ）[2]，其利用预报的风场资料，将第三代生成波模式应用于大尺度、长时间的浪高预测。然而，数值波浪模型是物理规律驱动的数值逼近模型，具有输入复杂度高、对风场资料的要求高及计算过程耗时长等特点，比较适用于大区域海浪的反演和预报。

由数据驱动的方法中，经典线性时间序列模型包括自回归模型（Autoregressive，AR）、自回归移动平均模型（Autoregressive Moving Average，ARMA）和差分整合移动平均自回归模型（Autoregressive Integrated Moving Average，ARIMA）等[3]。Soares 和Ferreira[4]将AR 用于浪高预测；Ge 和Kerrigan[5]对比了AR 和ARMA 用于海浪预报的性能，在10 种不同的海浪数据测试下，ARMA 的误差和效率均优于AR。Agrawal 和Deo[6]采用ARMA 和ARIMA 在不同预测区间进行在线浪高预测，结果表明ARMA 和ARIMA 的性能非常相似。但是ARMA 模型对序列的平稳性有要求，而ARIMA 能够通过差分运算将非平稳数据转换成平稳数据，解决平稳性依赖问题，所以ARIMA 模型是应用更为广泛的经典线性时间序列模型。

近年来，以大数据为基础的机器学习算法表现出强大的预测能力。Makarynskyy[7]和Cornegobueno 等[8]利用人工神经网络（Artificial Neural Networks，ANN）和极限学习机（Extreme Learning Machine，ELM）预测浪高，在准确率和一致性方面都有较好的表现。由于支持向量机（Support Vector Machine，SVM）和支持向量回归（Support Vector Regression，SVR）具有强大的泛化能力和完整的数学理论，在海浪预测方面也得到广泛应用[9-11]。Malekmohamadi 等[12]对SVM、ANN、贝叶斯网络和自适应神经模糊推理系统（Adaptive neural fuzzy Inference System，ANFIS）的浪高预测效果进行了深入研究，结果表明，ANN、ANFIS 和SVM 的预测结果都在可接受范围，而贝叶斯网络的预测结果相对不可靠。陆小敏等[13]通过集成栈式自编码器和XGBoost（eXtreme Gradient Boosting）[14]算法，进行有效波高预测，但是并没有考虑到数据分布的不平衡和数据集的规模大小。黄心裕等[15]基于Prophet 算法[16]对海南近海波高和周期进行了分析和预测。Prophet 算法是基于时间序列分解（Seasonal、Trend 及Residual）和机器学习的拟合实现的，适用于具有强烈季节性影响的时间序列分析，对数据异常和趋势变化具有稳健性。深度学习作为机器学习的子领域，极大地促进了计算机视觉和自然语言处理的发展。长短时记忆网络（Long Short Term Memory，LSTM）是最流行的时间序列预测深度学习网络之一，被广泛地用于预测风速、交通、太阳能和股票价格等[17]领域。莫旭涛和李自立[18]将卷积神经网络（Convolutional Neural Network，CNN）和LSTM 相结合，在中国南海北部湾的浪高预测取得较高的预测精度。顾兴健等[19]基于LSTM 建立的海浪环境短期预报模型，在我国海域上的预测结果取得了较好的精度，但是随着时间长度的推移，误差会逐渐增大。此外，许多新的深度学习网络，例如DeepAR[20]也被广泛应用到时间序列预测相关领域，但是在浪高预测中应用较少。

上述方法尝试从多个角度进行浪高预测，但未能充分考虑浪高序列的周期性、非平稳性和非线性，一定程度地限制了浪高预测的精度。基于局部加权回归（Locally Weighted Regression，Loess）的周期趋势分解（Seasonal and Trend decomposition using Loess，STL）[21]能够探索复杂的时序数据的规律，适用于时序预测任务，且具有较强的鲁棒性。为了实现对多站点未来12 h 的浪高预测，本文针对多源浪高时序数据的多周期性、非平稳性和非线性等特点，提出了一种基于多周期STL 分解和两级融合策略的浪高预测方法MSTL-WH。首先通过周期图法估计多源浪高数据集中的主要周期，然后利用STL 将复杂的浪高序列分解为简单的趋势项、周期项和余项，最后使用LSTM 结合两级融合策略以融合长中短时序下的浪高特征并进行浪高预测。应用实测浪高数据开展实验，并与经典时间序列模型ARIMA、加性时间序列预测模型Prophet、集成学习模型XGBoost、长短时记忆网络LSTM 和基于概率预测深度学习模型DeepAR。实验结果表明，MSTL-WH 能够对不同站点未来12 h 的浪高进行准确预测，综合表现优于ARIMA、Prophet、XGBoost、LSTM 和DeepAR 方法，各级浪高下MAE 均低于20%，符合业务化运行标准。

1 方 法

MSTL-WH 的流程如图1 所示。首先对浪高数据集进行预处理，包括缺失值填充、异常值处理等。使用周期图法提取浪高数据集中的4 个主要周期，以代表不同监测站点的浪高周期，并根据这4 个主要周期对浪高序列进行4 次STL 分解，将复杂的浪高序列分解为12 个简单分量；然后采用结合两级融合策略的LSTM 网络进行特征提取与融合，有效学习不同周期、不同时间海浪信息对未来浪高的影响；最后使用全连接层并结合注意力机制输出浪高预测值，实现对多站点浪高的精确预测。

图1 方法流程图Fig. 1 Flow chart of the proposed method

1.1 基于STL 的多周期-趋势分解

近岸浪高受多重因素影响，使得浪高难以预测，近岸浪高具有一定的周期性，可以使用STL 将浪高时间序列分解为3 个简单分量：趋势分量、周期分量和剩余分量。不同站点浪高时间序列一般具有不同的周期，因此本文利用从数据集中提取的4 个主要周期，对每一条浪高时间序列进行4 次STL 分解，提取其不同周期下的分量，从而提高预测方法的泛化性能，实现对多源浪高时间序列的精准预测。高序列X(n) ，对其进行离散傅里叶变换为X(ejω)，该序列的周期图可以定义为：

浪高数据主要周期提取的方法采用经典的周期图法，即信号功率谱密度估计方法。对于一个浪

根据式（1）得到的功率谱估值，找出最大功率对应的频率，并取其倒数得到该序列的主要周期。

STL 是由Cleveland 等[21]提出的一种经典的时间序列分解方法，其优点在于，对带有异常值的时间序列分解出的分量有更强的鲁棒性，本文中，STL 将浪高序列分解为3 个分量的分解表达如下：

式中： Xi为 浪高序列； Ci为趋势分量； Si为周期分量； Ri为剩余分量；N 为序列长度。STL 是一种迭代方法，其分解过程主要分为内循环和外循环，内循环嵌套在外循环中。内循环用于更新趋势分量和周期分量，外循环用于计算稳健的权值，通过在下一次内循环中使用这些权值，以减少异常值对更新后续内循环中趋势分量和周期分量的影响。内循环是STL 的主要部分，具体循环过程如下。

第1 步：去趋势性。在内循环迭代 k+1次 ，使用在第 k 次 迭代时得到的趋势分量对原始浪高序列进行去趋势：。

第2 步：平滑周期性。使用Loess 对去趋势浪高序列 Xi′的 每个周期子序列进行平滑，得到浪高序列的临时周期分量。

第4 步：临时周期分量去趋势性。将第2 步中得到的临时周期分量减去防止低频信号进入周期分量，得到第 k+1次 循环的周期分量，表示为。

第5 步：去周期性。原始浪高序列 Xi减 去周期分量得到去周期序列，表示为。

第2、3、4 步是内循环的周期平滑部分，第6 步是趋势平滑部分。在外循环中，利用内循环所得的浪高趋势分量和浪高周期分量来计算浪高剩余分量。浪高序列 4 个主要周期经过STL 分解，被分解为12 个简单分量，接下来以这12 个分量作为神经网络预测模型的输入。

1.2 两级融合策略

对于不同周期STL 分解的12 个分量，直接利用LSTM 进行特征学习可能会破坏各周期的独立性，造成多周期之间的干扰。为此，结合两级融合的思想设计特征学习网络，网络第一层使用4 个LSTM 网络分别提取4 个不同周期输入子序列的特征。

LSTM 网络是RNN 的一种改进模型，相较于RNN 模型，它具有特殊的记忆和遗忘模式，每一个LSTM 网络拥有一个记忆单元（cell），在 t 时刻的状态记为 ct，其值通过输入门、遗忘门和输出门更新，它们一般使用sigmoid 或者tanh 函数进行激活。记忆单元的工作流程为：在时刻t，记忆单元通过3 个门接收当前状态 xt与 上一时刻记忆单元的隐藏状态 ht-1，除此之外，每一个门还接收记忆单元的状态 ct-1。接收到输入信息之后，每一个门对不同来源的输入进行计算，并且由其激活函数决定其是否激活。输入门的输入经非线性变换后，与经过遗忘门处理过的记忆单元状态进行组合，产生新的记忆单元状态 ct。最后，记忆单元状态 ct通过非线性运算和输出门的控制产生记忆单元的输出 ht。

从浪高时间序列的长、中、短周期考虑，结合两级融合的思想设计预测网络，网络第一层使用4 个LSTM 网络分别提取输入序列中4 个子序列的特征，然后将输出融合到一个LSTM 网络中，之后再连接2 层LSTM 网络进一步提取特征（LSTM 网络中的隐藏单元数量均为128）。

1.3 自注意力机制

对浪高特征进行充分提取之后，每个特征已经获得了一定的权重，为进一步强化特征，提升模型预测精度，使用自注意力模块对权重进一步分配。

注意力机制本质为一个查询对应多个键值对的映射。注意力机制的原理可分为3 个阶段：第1阶段计算每一个查询Q 和各个键K 的相似度，获得每个键对应值V 的权重；第2 阶段使用Softmax激活函数归一化权重，从而获得权重系数；第3 阶段对权重系数和对应的键值V 进行加权求和，获得最终注意力权值，其计算式为：

式中： Q ∈Rn×dk； K ∈Rn×dk； V ∈Rn×dk， n为 输入序列长度， dk为输入序列特征维度。

自注意力机制也被称作内部注意力机制，是一种特殊的注意力机制。一般情况下，注意力机制中的输入和输出是不一样的，比如在翻译任务下，输入序列是需要翻译的英文语句，输出序列则是翻译后的中文语句，注意力机制发生在输出的Q 和输入的所有元素之间。对于自注意力机制则是发生在输入序列或输出序列的内部元素之间，也就是式（3）中Q、K 和V 三个矩阵都来源于相同的输入序列。自注意力机制可以减少对外部信息的依赖，将输入序列不同位置的信息关联，擅长提取数据的内部相关性。

2 实验验证

实验验证了MSTL-WH 在测试集和新数据集上的预测误差，并通过与ARIMA、XGBoost、Prophet 和LSTM 这4 个具有代表性的预测方法对比，证明本文所提方法的优越性。本文实验硬件环境如下：处理器为英特尔酷睿i9-10885H，CPU 频率为2.4 GHz，内存为16 GB；操作系统为Windows10（64 位）；程序设计语言为Python3.6.9（64 位），集成开发环境为PyCharm Professional 2019.3.3；程序设计过程中的LSTM 网络由Keras2.1.5 程序包实现。整个浪高预测实验主要分为4 部分：①数据集构建；②消融实验；③对比实验；④泛化性能验证。

2.1 评价指标

为验证MSTL-WH 的有效性，选择平均绝对百分误差（Mean Absolute Percentage Error，MAPE）和平均绝对误差（Mean Absolute Error，MAE）作为评价指标，对比不同预测模型预测浪高的性能。MAPE 和MAE 的公式如下所示：

式中： yi为 真实浪高；为预测浪高； Nt为预测长度。模型在预测浪高时，MAPE 和MAE 的数值越小，代表预测结果越准确。

2.2 数据集构建

本文的浪高实测数据来自国家海洋科学数据中心[22]。由于浪高监测设备异常或网络异常等原因，实测数据会包含异常值，因此需要对实测数据进行异常值处理，具体处理方式为：对于异常值连续长度不超过3 的浪高序列，使用异常点前后的3 个有效值的均值进行填充；对于异常值连续长度超过3 的浪高序列进行截断保存。对所有站点的实测数据进行上述处理后，得到94 条长度不一的浪高序列，这些序列用于后续数据集的制作。

数据集中的观测站点分布在24°～39°N，包含小长山（XCS）、小麦岛（XMD）、连云港（LYG）、大陈（DCH）、老虎滩（LHT）、芝罘岛（ZFD）、南麂（NJD）七个海洋站的实测数据，每条浪高数据时间跨度为2017 年1 月至2020 年4 月，采样频率为1 次/h，共29 160 h。

由于浪高实测数据跨越了不同海区，其浪高数据的周期性变化也大不相同。为了确定对浪高数据进行STL 分解的周期值，使用周期图法对每一条浪高序列进行功率谱密度估计。提取功率最大的频率，取其倒数作为候选周期，共获得94 个候选周期，各观测站点浪高时序数据的主要周期如图2 所示。结合候选周期的直方图，最终确定140、221、314 和460 h 作为周期值。根据上述4 个周期，STL 将每一条复杂的浪高序列分解成12 个简单分量，将每个分量归一化至区间（0，1）后用于后续的数据集制作。为了捕捉不同站点的海浪周期，从而更加准确地预测浪高，在制作数据集时，滑动窗口的长度应大于海浪序列数据的周期。因此，在使用滑动窗口切分浪高序列时，窗口大小设置为500 h，步长为2 h，前488 个时间点的浪高值及其分量作为输入，后12 个时间点的浪高值作为真值，对所有序列进行滑动窗口切分后，共得到69 836 个样本。按照8∶2 划分训练集和测试集，得到55 868 个样本的训练集、13 967 个样本的测试集，数据形状分别为（55 868，488，12）和（13 967，12），训练集中各等级浪高样本的数量如图3 所示。

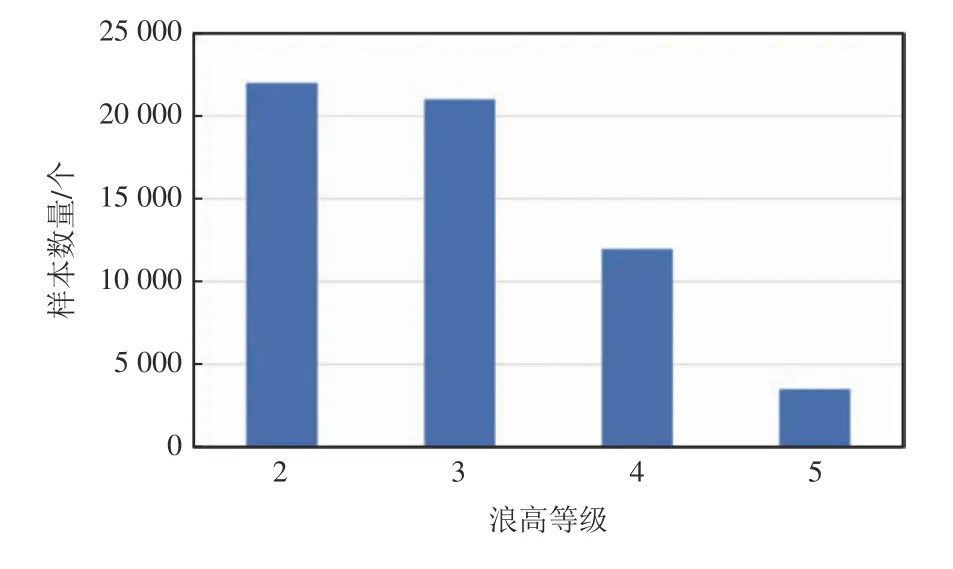
图3 训练集中各等级浪高的样本数量Fig. 3 Number of samples at different levels of wave height in the training data set

2.3 消融实验

首先通过对比实验，确定一个具有3 层LSTM 的预测网络，基于此网络对比采用单周期STL 分解前后和多周期STL 分解的浪高预测误差，验证多周期STL 分解的有效性，然后分别在是否采用多周期STL 分解的基础上，对比采取两级融合前后的浪高预测误差，证明两级融合的有效性，最后通过实验确定融合层后LSTM 的层数。

为了验证多周期STL 分解的有效性，向一个3 层LSTM 预测网络分别输入原始浪高时间序列、单周期STL 分解后的浪高时间序列和多周期STL 分解后的浪高时间序列，对比浪高预测误差，其中每层LSTM 的隐藏神经元个数为128。未采用STL 分解时，模型输入数据为原始浪高序列，维度为（488，1）；采用单周期STL 分解时，使用周期图法得到数据集中功率最大周期，并据此对输入的浪高序列进行STL 分解，模型的输入数据维度为（488，3）；采用多周期STL 分解时，模型的输入数据维度为（488，12）。模型的输出均为未来12 h 的浪高值，结果如表1 所示。

表1 多周期STL 分解对预测性能的影响Table 1 Impact of multi-period STL decomposition on prediction performance

从表1 可以看到，使用单周期进行STL 分解在一定程度上可以减小预测误差，相比之下，多周期进行STL 分解可以更进一步减小预测误差，使MAE 降至0.15 m，MAPE 降至30.97%，这表明多周期STL 分解对于减小预测误差发挥了重要作用。

接下来为了验证两级融合的有效性并进一步说明多周期STL 分解的有效性，我们分别对单周期STL 分解及多周期STL 分解下是否采用两级融合对预测误差的影响进行了对比。在融合层之后连接1 层LSTM 网络和1 层全连接层来输出浪高预测值，其中每层LSTM 的隐藏神经元个数为128。实验结果如表2 所示。

表2 单/多周期STL 分解下两级LSTM 特征融合对预测性能的影响Table 2 Impact of two-stage LSTM feature fusion on prediction performance under single/multi-period STL

从表2 可以看出，无论在单周期STL 分解下还是在多周期STL 分解下，采用两级融合均可明显减小预测误差。相对单周期STL 分解，采用多周期STL 分解具有更小的预测损失，结合两级融合可将MAE 降低至0.11 m，MAPE 降低至20.56%。因此，多周期STL 分解及两级融合对于多源浪高时间序列预测任务具有明显提升效果。

最后，在采用多周期STL 分解及两级融合的基础上，我们在特征融合层后连接不同层数的LSTM，然后使用自注意力层对权重再分配，最后连接1 个全连接层输出浪高预测值，其中每层LSTM 的隐藏神经元个数为128，结果如表3所示。

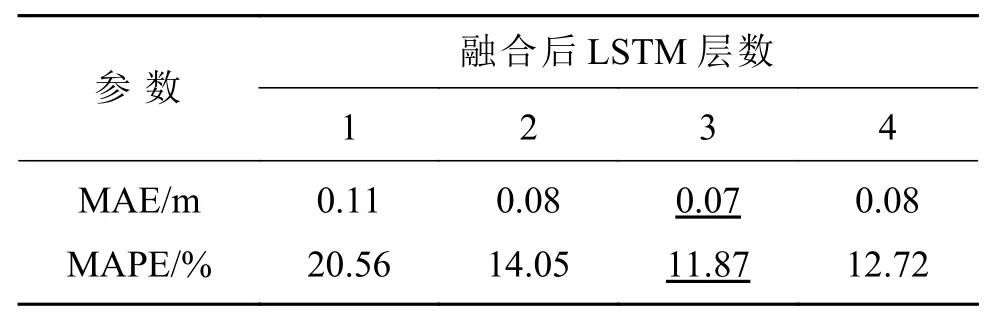
表3 LSTM 层数对预测性能的影响Table 3 Impact of the number of layers of LSTM on prediction performance

由表3 可以看出，随着网络中LSTM 层数的增加，网络的预测性能也随之提升，但当LSTM层数增加至4 层时，由于网络参数量过多导致过拟合，网络性能开始下降，当LSTM 的添加层数为3 时，模型的预测误差最小，MAE 低至0.07 m，MAPE 低至11.87%，因此，在MSTL-WH 中，使用3 层LSTM 进一步提取融合后的特征。

2.4 对比实验

基于时间序列的预测模型主要包括经典线性时间序列模型、机器学习模型和深度学习模型，本文从中选取了ARIMA、Prophet、XGBoost、LSTM 和DeepAR 这5 个具有代表性的预测模型与MSTLWH 进行对比。

根据最新发布的海浪等级国家标准[23]，将模型预测结果计算平均值后分为4 个等级区间，即2级对应浪高0.10～0.50 m、3 级对应浪高0.50～1.25 m、4 级对应浪高1.25～2.50 m、5 级对应浪高2.50～4.00 m，评价指标结果如表4 所示。同时，为直观观察各模型在不同等级浪高下的预测性能，在不同浪高等级范围随机选择了4 个时间序列，使用各种对比模型进行了24 h 预测，预测结果如图4 所示。

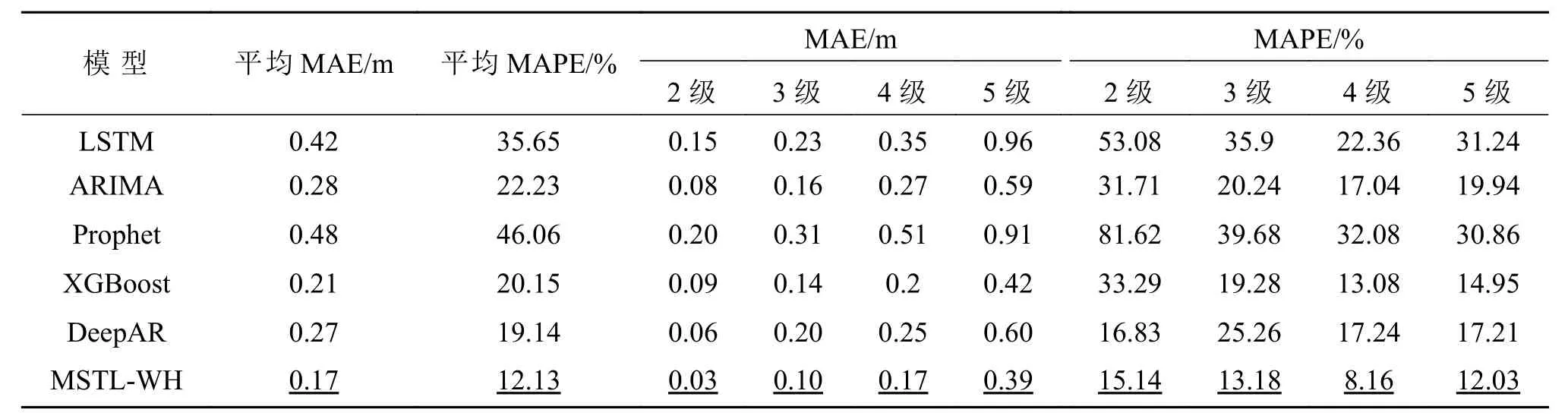
表4 各模型在不同浪高等级下的评价指标结果Table 4 Evaluation metrics of different models at different levels of wave height

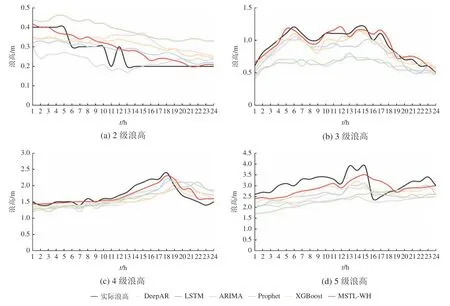
图4 各模型不同等级浪高下的预测效果Fig. 4 Results of different models at different levels of wave height

根据24 h 的浪高值预测结果对比（图4），MSTL-WH（红色）与实际浪高值（黑色）的拟合度较高。集成学习方法XGBoost（黄色）和经典的ARIMA 模型（蓝色）整体上比其他3 种方法性能更好。DeepAR 模型（粉色）整体性能与ARIMA 模型类似。Prophet 模型（绿色）对低等级的浪高预测值偏高，但是高等级的浪高预测值偏低，说明其对数据变化适应性较差。同样，LSTM 网络（灰色）预测网络效果也不佳，总体预测值偏低，这对海浪预警非常不利。最后，大部分模型在海况4 级的浪高范围内预测趋势较好，这可能与这一等级的训练数据较充分有关，但也存在波动峰值滞后的情况，本文模型滞后性较小。

表4 从误差指标上进一步给出客观评价。MSTL-WH 在各等级浪高下的预测指标均优于其他模型，尤其对于3、4 级浪高，即在0.50～1.25 m、1.25～2.50 m 区间的浪高序列，MSTL-WH 的平均绝对误差仅为0.10 m 和0.17 m，在平均绝对误差±0.20 m 的误差范围内，浪高等级不会发生变化。对于2 级浪高，MSTL-WH 的平均绝对误差仅为0.03 m，几乎可以忽略不计。因此，本文提出的MSTLWH 在各等级浪高下有着良好的预测性能，满足浪高预报业务化的要求（MAPE≤20%）。

2.5 泛化性能验证

尽管MSTL-WH 在验证集上的准确性和稳定性表现良好，为了进一步验证其泛化能力，本文在不同站点以及新数据集上分别进行了实验。各模型针对不同站点（多源）的MAE 评价指标结果如表5 所示。

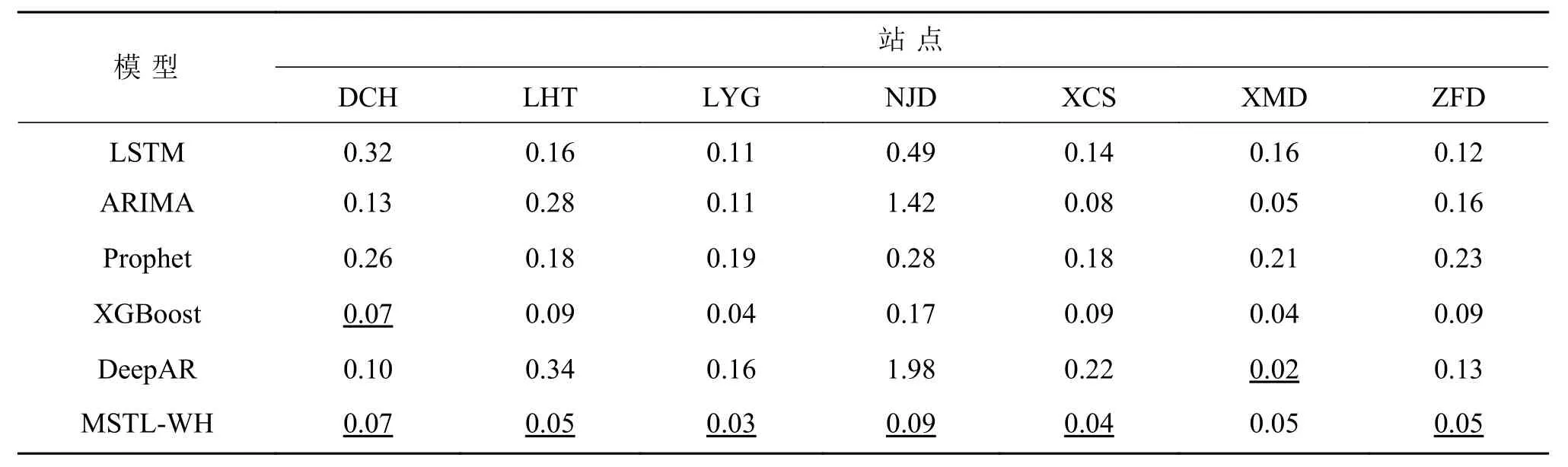
表5 各模型在不同站点（多源）的MAE 评价指标结果（m）Table 5 MAE evaluation metrics of different models at different stations (m)

由表5 可以看出，MSTL-WH 在7 个不同站点中有5 站MAE 评价指标上优于其他模型。在DCH站点，MSTL-WH 和XGBoost 的预测指标相同，均优于其他模型。在XMD 站点中，DeepAR 的MAE 评价指标更小，预测性能相对更好，但MSTL-WH 仍然是所有预测模型中排名第二的模型。总体来看，MSTL-WH 在不同站点（多源）的预测误差变化小，模型性能稳定。

对国家海洋科学数据中心与训练集一致的7个站点2020 年4 月至5 月的浪高实测数据进行预处理（详见2.2 节描述）后，共得到3 620 条浪高序列，覆盖了2～5 级的浪高。MSTL-WH 在这一新数据集上的各项指标如表6 所示。

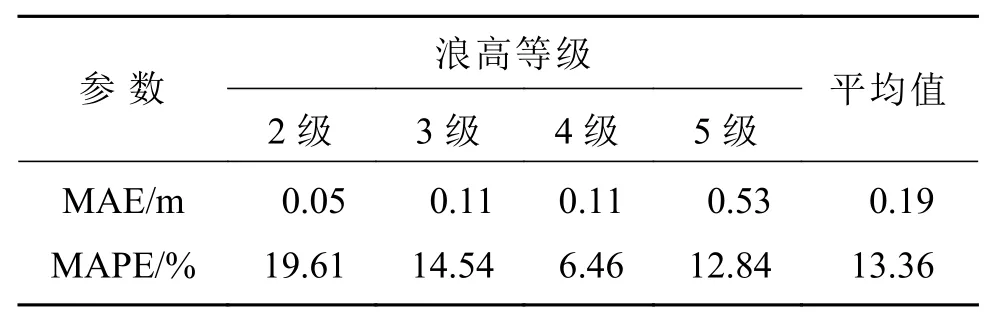
表6 MSTL-WH 在新数据集上的各项指标Table 6 Results of MSTL-WH in new dataset

由表6 可见，MSTL-WH 在新数据集上各等级浪高的平均相对误差均小于20%，对比表4 中的性能指标，MSTL-WH 除了在2 级浪高预测有较大误差外，其余等级浪高情况下最大增加了1.36%的平均绝对误差。虽然2 级浪高预测的MAPE 为19.16%，但其平均绝对误差仅为0.05 m，对实际预报业务几乎没有影响。由此可见，MSTL-WH 在不同等级浪高预测上具有良好的泛化性。

3 结 语

本文基于浪高实测数据，针对多源浪高时序序列难以预测问题，提出了基于多周期STL 分解和两级融合策略预测方法。首先使用周期图法从多源浪高时序数据集中提取主要周期，并据此对浪高序列进行STL 分解，然后使用LSTM 从短、中和长期不同的视野提取浪高特征，采用两级融合策略进行特征融合，最后使用全连接层输出未来12 h 的浪高值。

本文所提出的浪高预测方法MSTL-WH 对2、3、4 和5 级浪高序列预测的MAPE 均低于20%，满足浪高预报业务化运行的要求（MAPE≤20%）。相较于LSTM、ARIMA、Prophet、XGBoost 和DeepAR，MSTL-WH 能更好地预测具有不同周期的浪高序列，同时解决了对不同地区（多源）预测适应性差的问题，降低了预测模型的滞后性，且在新的浪高数据集下，具有良好的泛化性。

在充分分析时间序列数据特征的前提下，本文提出的方法不仅适用于浪高预测，还可以用于其他领域的时间序列预测任务，具有广阔的应用前景。