波-流相互作用源函数及其对海浪模拟的影响

王泽宇，江兴杰*，华 锋，杨永增

（1. 自然资源部 第一海洋研究所，山东 青岛 266061；2. 自然资源部 海洋环境科学与数值模拟重点实验室，山东 青岛 266061；3. 山东省海洋环境科学与数值模拟重点实验室，山东 青岛 266061；4. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室，山东 青岛 266237；5. 汕头大学 理学院，广东 汕头 515063）

海浪和海流都是海洋动力环境的重要组成部分，二者之间存在着动量、能量的交换，可统称为波-流相互作用（wave-current interaction）。Johnson[1]在假设浪、流间没有能量交换且波能守恒的前提下，通过研究线性深水波以及其与波向成任意夹角的海流耦合，观察波-流相互作用对波浪折射的影响。Arthur[2]对Johnson[1]的理论进行进一步研究，建立了一种动态耦合，认为浪、流之间有能量的交换，不能保持各自能量的守恒。Longuet-Higgins 和Stewart[3-4]在波致沿岸流的理论研究中，首先提出波-流相互作用的理论，并推导出了浅水区的二维波应力表达式。Bretherton 和Garrett[5]认为，对于运动介质中传播的小振幅无耗散短波动，波作用量密度不变。Phillips[6]指出，在非均匀流场中，波浪与平均流动之间存在着能量交换，一般来说波能密度并不守恒，但波作用量（wave action）是守恒的；在此基础上波作用量守恒原理被应用于表面波，进而导出了波能平衡方程以及平均流动的能量平衡方程。

波-流相互作用对波浪发生、成长以及传播的影响亦被引入海浪数值模拟中。在Wave Modeling（WAM）[7]、WaveWatchIII[8]、Simulating Waves Nearshore （SWAN）[9-10]为代表的第三代海浪模式中，通常求解的是波作用量形式的能量平衡方程；由于波作用量在波-流相互作用中是守恒的，所以仅需考虑背景流场对海浪群速度大小、方向的改变，以及所引起的波浪折射效应，没有单独讨论流场对波浪能谱的影响。波-流相互作用源函数（wave-current interaction source function）[11-13]以Phillips[6]导出的波能平衡方程、平均流动的能量平衡方程为基础被推导出来，从理论上将波-流相互作用中流场对波浪能谱的改变与对波浪能量传播的影响分开讨论。Wang 等[14]以波-流相互作用源函数[11-13]为基础，引入应变速率、散度和变形速率的概念，分别从这3 个方面研究了背景流场对海浪的影响；但其分析过程中仍没有将流对波浪传播与对能谱的影响区分开。

综上所述，波-流相互作用对波浪模拟的影响可包含2 个方面：①背景流场的存在可影响波浪能量的传播，包括改变群速度的大小、方向，以及产生折射效应；②振动运动对抗非均匀流场中水平流动的流速切变（即流速梯度∂U⇀/∂X⇀=∂(Ux,Uy)/∂(x,y)）做功，可使海浪能谱发生改变。在以往的研究中，对波-流相互作用的探讨主要围绕前者进行，鲜见对后者的讨论。

本文在袁业立等[11-12]所建立的波-流相互作用源函数（以下统一称为 Scu）的基础上，通过对该源函数的系统分析，以及利用MASNUM 海浪模式[11-13]所进行的理想实验，阐释该源函数对海浪模拟可造成的影响。本文首先分析了水平流动的流速梯度量级、水深以及波浪成长状态对 Scu作用效果的影响，然后进一步分析了 Scu在谱空间中的作用形态，最后在MASNUM 海浪模式的基础上进行理想实验，分析 Scu对波浪参数有效波高、谱峰方向模拟的影响。

1 波-流相互作用源函数

波-流相互作用源函数（ Scu）可写成以下形式：

式中：E 为单位截面所含的平均总扰动能量； Ux、 Uy分别为流速在x、y 方向的分量；流梯度矢量表示浪场空间内两点间流向量（流速、流向）的变化情况，即， 由此 ∂Ux/∂x、∂Uy/∂y、 ∂Ux/∂y、 ∂Uy/∂x 分别为 Ux、 Uy在x、y 方向的流速梯度； S1、S2、S3、S4分别为与 ∂Ux/∂x、∂Uy/∂y、 ∂Ux/∂y、 ∂Uy/∂x 一一对应的波流相互作用函数的系数；为波数矢量； cg和c 分别为谱空间中波数矢量所对应的群速度和相速度； θ 为所对应波向，即：

由频散关系可得：因此，从 Scu的推导过程中可以得出，其表示波浪对抗平均动量流（流速、流向）的变化做功，波浪与平均动量流之间存在能量的交换。

1.1 流速梯度量级对 Scu作用效果的影响

考虑实用形式的JONSWAP 谱[15-16]， S(f)为一维频谱，有

式中：有效波高 H1/3取 6.5 m[15-16]；谱峰周期 Tp取 10 s[15-16]；峰升因子 γ=3.3[15-16]；形状参数取值为

图1 不同流速梯度量级下波-流相互作用源函数（ Scu）、波-波非线性相互作用源函数精确计算结果（ Xnl ）及破碎耗散源函数（ Sds）的量级对比Fig. 1 Comparison of wave-current interaction source function (S cu) , exact computation of nonlinear energy transfer ( Xnl ) and dissipation source function (S ds)

1.2 水深和波浪成长状态对 Scu作用效果的影响

由式（8）可知，在深水条件（d→ ∞） 下 cg/c→ 1 /2， 而在浅水条件（d→0）下 cg/c→1，因此，式（1）～式（5）中的参数 cg/c在 不同水深下可能使 Scu的作用效果发生改变。此外，式（8）还表明， cg/c与波数k 也密切相关；由于k 随着波浪的成长会出现由大到小的演变，因此参数 cg/c对 Scu的影响还可能随波浪成长的状态不同而相异。图2 为 ∂Ux/∂x=10-5s-1、 水深10～2 000 m 时， Scu的系数 S1随频率/波数的变化趋势，频率范围为：0～1 Hz，对应的波数最小为0，最大值可由式（7）计算得到。由图2 可见，在高频（大波数）的区间内，各水深下 S1基本一致，几乎不随频率/波数变化，也就是说，对于成长初期的海浪，水深效应基本不会影响 S1对波浪模拟的作用效果；而随着海浪成长得越来越充分（低频、小波数区域），不同水深下 S1的 差别开始显现，且水深越浅， S1开始变化的频率（波数）相对越大，至海浪模拟谱空间设置的最低频率（通常为0.030 或0.042 Hz）。除2 000 m 深水情况外，其他各水深下 S1的值与高频部分相比都发生了较大的改变；而就深水情况而言，在一般海浪模拟的谱空间范围内，海浪的成长状态不会影响 Scu对海浪模拟的作用效果。

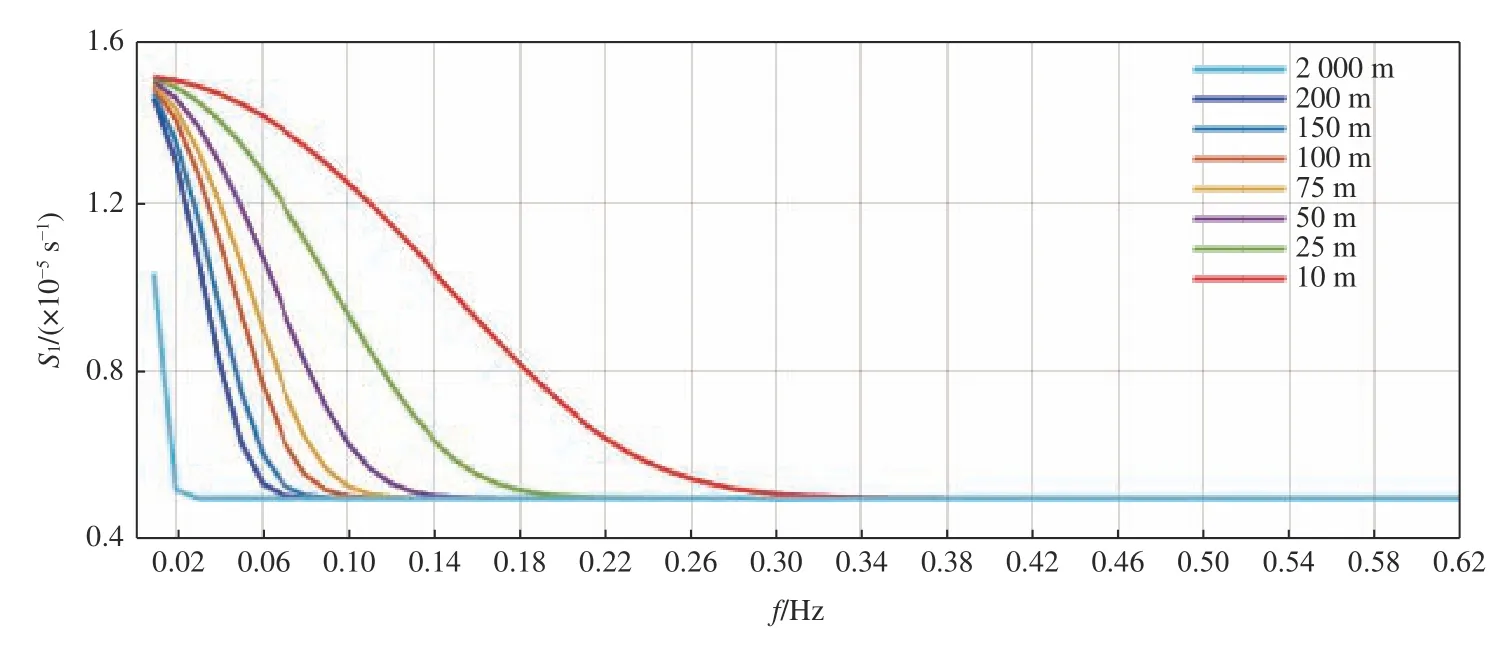
图2 ∂ Ux/∂x=10-5 s-1时 不同水深下 Scu系 数 S1随频率（波数）的变化趋势Fig. 2 Trends of the coefficients S 1 varying with frequency (wave number) under different depth conditions (∂ Ux/∂x=10-5 s-1)

1.3 Scu在波谱空间中的作用效果

为避免水深和波浪成长状态的影响，以下的分析和理想实验均在深水条件下展开。图3 为当cg/c=1/2 时 ，Scu（ S1～S4）在谱空间范围内的取值情况，其中正值为海浪谱获得能量（红色），负值为海浪谱失去能量（蓝色）。从式（1）～式（5）可以看出，S1～S4紧密依赖于三角函数sin θ、cosθ在谱空间方向上的取值。当∂Ux/∂x 分别为10—5或—10—5s—1，S1系数在谱空间所有方向上≤ 0或≥0，即∂Ux/∂x分量可使 Scu令波谱能量在整个谱空间范围内减小或增加（图3a 和图3b）；同时，由于 cos2θ 和 sin2θ在[0°,360°]范围内的取值在[0,1]范围内变化，S1对波谱的作用在0°（360°）和180°最为明显，而在90°和270°时没有影响；类似的效果也体现在 S2上，如图3c和图3d 所示（∂Uy/∂y分别为10—5和—10—5s—1）。同理，当∂Ux/∂y取10—5或—10—5s—1时，由于sinθ、cosθ在[0°, 360°]范围内的取值可在[—1, 1]范围内变化， S3对 波谱能量的改变在不同谱空间方向上也会发生变化： S3对海浪谱的作用在0°（360°）、90°、180°和270°上总有一项为零，因此S3对海浪谱的这几个方向没有影响，而在上述几个方向的间隔区间内，交替出现了增加和减少波谱能量的效果（图3e 和图3f）；类似的效果也体现在S4上，如图3g和图3h所示（∂Uy/∂x 分别取10—5和—10—5s—1）。此外， S1、S2对海浪谱的作用效果显然要比S3、S4更 显著；且由于上述作用效果在方向上的不均匀性， Scu不仅可增加或减小谱空间中的能量，也可造成谱峰方向的改变（详见第2 节理想实验）。

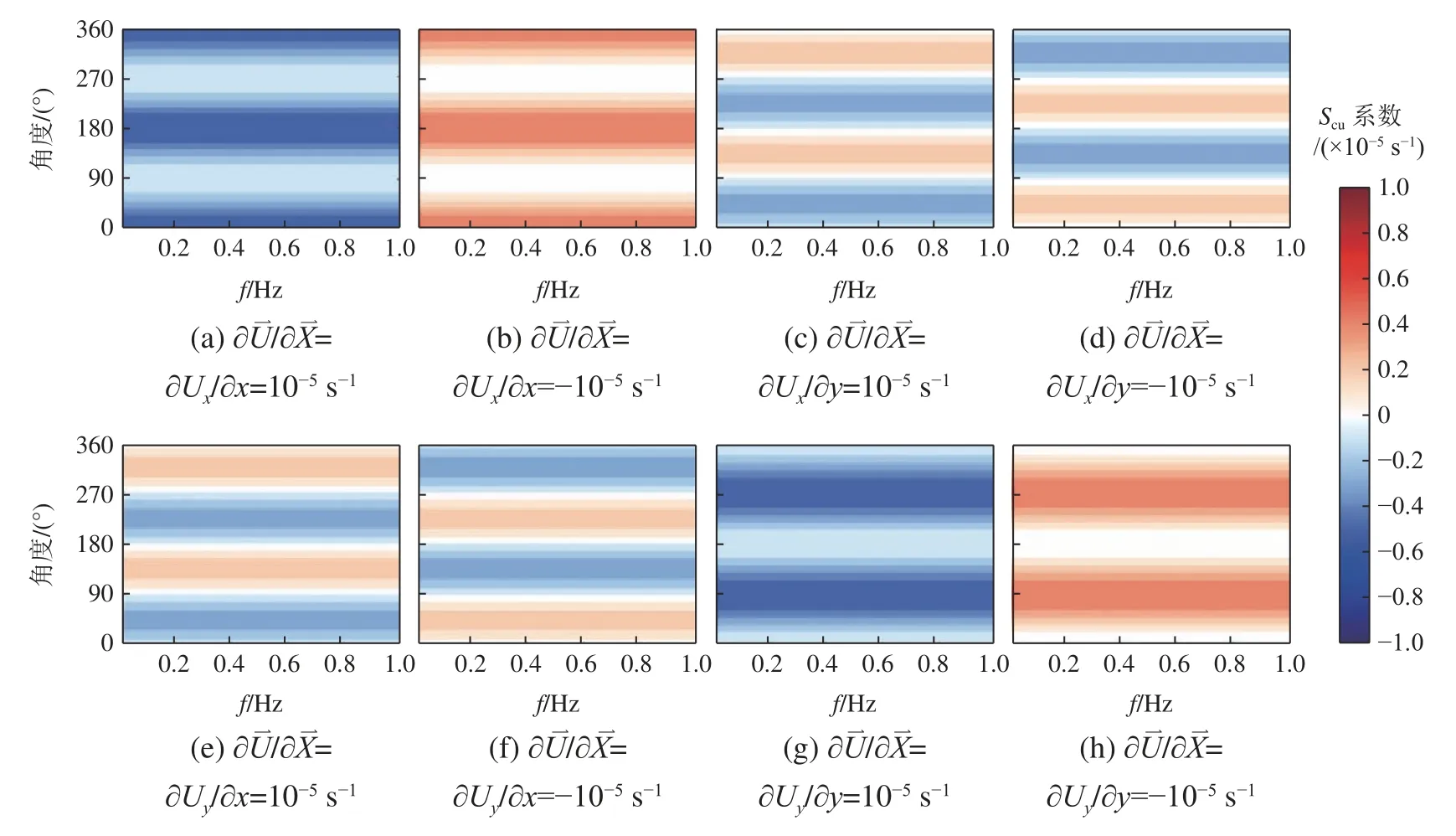
图3 S cu系数在谱空间中的作用效果Fig. 3 Patterns of coefficient Scu in spectral space

2 波-流相互作用源函数理想实验

2.1 理想实验方案设计

为了更符合实际状况，本文考虑海浪在传入流速变化区（关注区）后，模拟浪场在有、无Scu作用下的分布，比对其差异。主要比对有效波高Hs和谱峰波向dp两个模拟值，其中通过模拟谱的零阶矩获得 ：Hs

取一维频谱S（fp）中谱峰（谱密度最大值）频率 fp所对应方向 dp：

且约定为笛卡尔坐标系下的去向；比对结果统一为有 Scu作用时减去无 Scu作用时模拟值差值。就理想实验条件而言，为方便表述，考虑沿流向上2 个空间点的流向量变化：首先，将流向分为沿x 轴正向、x 轴负向、y 轴正向及y 轴负向四类情况；其次，在每个流向上再考虑流速梯度的方向，也将其分为沿x 轴正向、x 轴负向、y 轴正向和y 轴负向，如此，共形成16 组流场实验条件，所有实验流场方向及对应的梯度方向如图4 所示。图4 中，箭头方向表示流速方向，箭头长度表示流速相对大小：左侧2 列方案中，流速方向与流速梯度方向平行，而在右侧2 列方案中，流速方向则与流速梯度方向垂直；以方案a 为例，其流速方向与流速梯度方向一致，均沿x 轴正向，而方案e 中流速方向与流速梯度方向相反，流速梯度方向沿x 轴负向；方案c 中流速方向沿y 轴正向，而流速梯度方向沿x 轴正向。

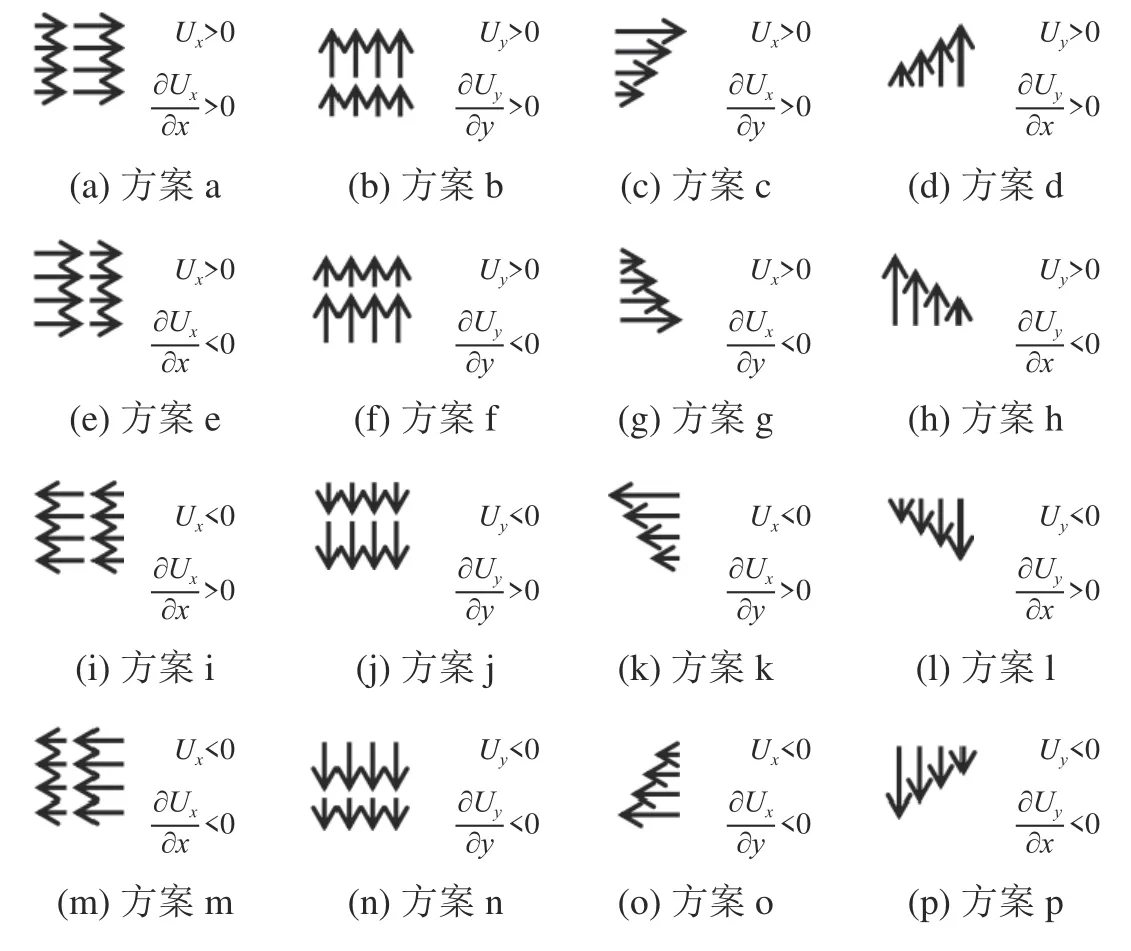
图4 实验流场方向及对应的流速梯度方向Fig. 4 The experimental flow directions and the corresponding gradient directions

理想实验的计算区域大小为1 000 km×1 000 km，在整个区域中均采用2 000 m 的等深地形，避免水深及波浪成长状态导致Scu的作用效果产生变化；流速变化区，即实验的关注区，设置在计算区域的中央。考虑（台风中心区域流速梯度量级[22]）和（Scu与 Xnl、对应的是25km×25km 的关注区域（图5b）。以方案a为例，流速在关注区域左边界布，设置2 个不同的关注区域：对应的关注区域大小为200km×200km（图5a），Sds具 有相同量级）两种不同量级的流速梯度，为了使2种量级的流速梯度均符合实际流场的空间分为0 m/s，流速沿x 轴增大，在关注区域的右边界，图5a 中流速达到2 m/s，而图5b 中则达到2.5 m/s；方案b 中，流速在关注区域下边界为0 m/s，流速沿y 轴增大，在关注区域的上边界，图5a 中流速达到2 m/s，而图5b 中则达到2.5 m/s。

2.2 10-5 s-1 流速梯度量级下Scu对模拟结果的影响

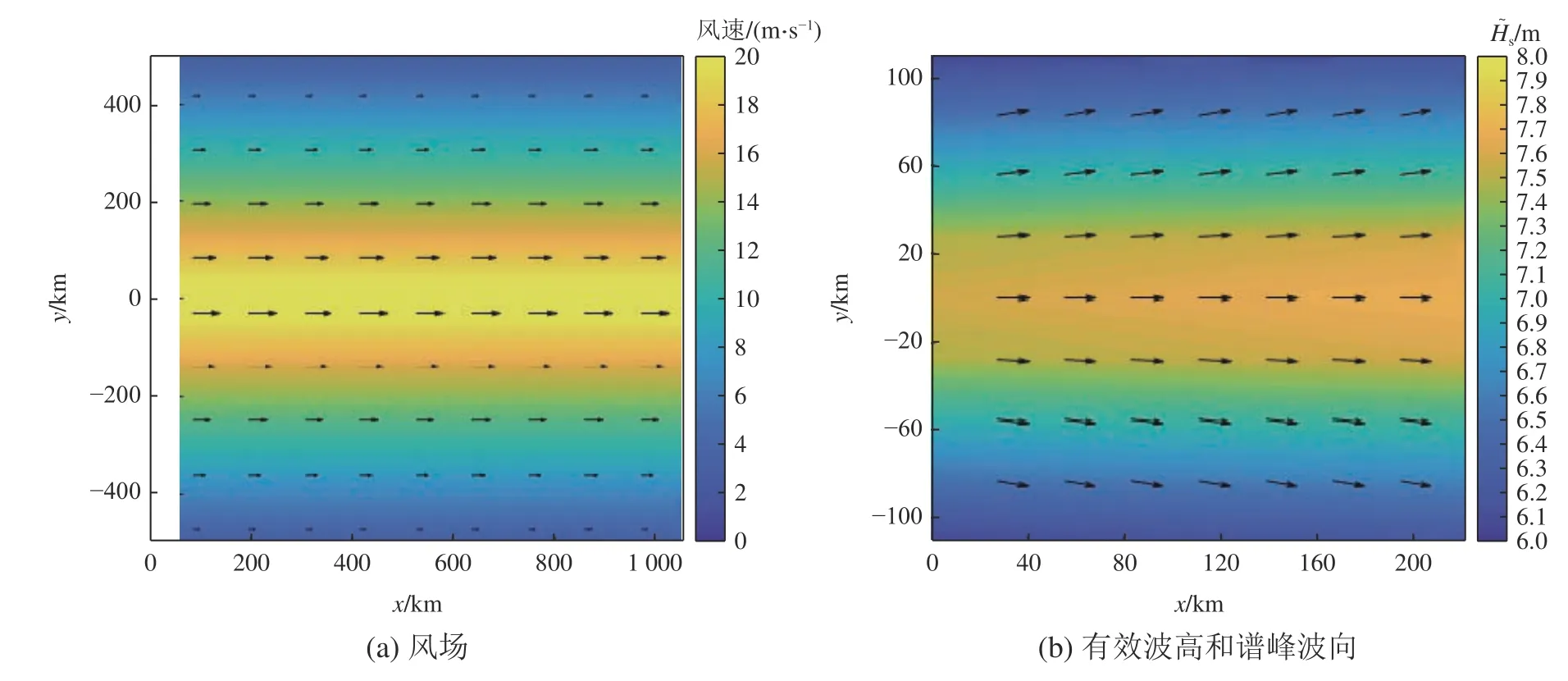
图6 不考虑 Scu时 的驱动风场和模拟72 h 后关注区域的有效波高和谱峰波向Fig. 6 Wind field and the simulated significant wave height and peak direction after 72 hours

图7a～图7p 和图8a～图8p 分别对应方案a～方案p 模拟72 h 后关注区域中和的 分布情况。图中，红色表示考虑了 Scu作用后的ΔHs值 增大，Δdp表现为逆时针偏转；蓝色表示在 Scu作用下ΔHs值 减小、Δdp顺时针偏转；白色则表示 Scu对 Hs、 dp的模拟无影响。图9 为图7和图8 中的A～L 点和M～X 点所对应的 Scu的谱空间分布（图9a～图9h 对应图7a～图7h 和图8a～图8h，图9 各分图中上、中、下三个部分分别对应图7 和图8 各分图中自上而下标识的3 个点，其中中间点均在x 轴上），其中黑色虚线表示谱峰方向，蓝色表示 Scu在该谱空间范围内值为负（能量减少），红色则表示 Scu在空间内为正（能量增加）。

图7 模拟72 h 后关注区内ΔHs的分布Fig. 7ΔHs distribution in the region of attention after a 72-hour simulation

图8 模拟72 h 后关注区域内Δdp 的分布Fig. 8Δdp distribution in the region of attention after a 72-hour simulation

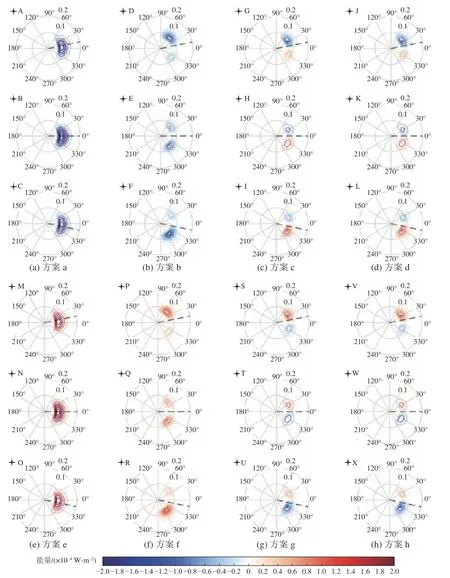
图9 图7、图8 中A～X 点 Scu的 谱空间示意图Fig. 9 Patterns of S cu at A-X in Fig. 7 and Fig. 8

从图7、图8 可以看出，首先，在不考虑背景流场影响波浪传播的前提下， Scu对波浪模拟的作用效果与流向无关，因此，图4 中前2 行的实验方案（对应图7a～图7h 和图8a～图8h）与后2 行的实验方案对应图7i～图7p 和图8i～图8p）实验结果相同。

其次， Scu对 Hs模 拟的影响显然与 Scu在谱空间中的分布形态以及 dp的位置有关。如图7a 和图7e所示，当流向与流速梯度方向一致或相反时，考虑 Scu的作用后 Hs模拟值在整个关注区域内减小或增大；对应图9a 和图9e 中关注点A～C 及M～O 的 Scu谱空间取值情况可见， Scu谱值在关注区域内均为负值或正值；依据袁业立等[11-12]、杨永增[13]以及Phillips[6]，可推测振动运动对抗背景流场中的流速梯度做负功或正功，因此导致整个海浪谱失去或获得能量；同样的原理适用于图7 左侧2 列所示的所有8 组实验。此外，在方案a、方案e、方案i、方案n 中，由于 dp与 梯度方向基本一致，Scu的作用效果最为明显（对应图3a、图3b 中0°（360°）、180°方向），而方案b、方案f、方案j、方案n 中，由于 dp与 梯度方向呈90°夹角， Scu的作用效果相对较弱（对应图3g、图3h 中0°（360°）、180°方向）；因此，图7 左侧2 列ΔHs的改变程度出现了明显的区别。而如图7 右侧2 列所示，当流向与流速梯度方向垂直时，ΔHs在 关注区域中y=0 两侧出现截然相反的变化趋势；ΔHs出现上述分布形态的原因仍然与 Scu分布及 dp的 位置有关，以图9c 为例：从图9c 中可以看到，图7c 中G～I 点上的 Scu系数谱空间分布对应图3c：在G 点上，由于 dp相 对0°向逆时针方向偏转，导致 Scu谱空间中负值的占比明显大于正值（图9c 上图），因此G 点一侧的ΔHs＜0 ； 同理，在I 点一侧ΔHs＞0 是 由于该侧 dp相对0°向顺时针方向偏转，导致 Scu谱空间中正值占比明显大于负值（图9c 下图）；而在H 点，由于 dp正在0°方向， Scu谱空间的正负值占比在 dp两侧完全对称（图9c 中图），因此在H 点所在的y=0 线上对谱能量的积分结果ΔHs=0。受篇幅所限，图7d、图7g～图7h、图7k～图7l 以及图7o～图7p 中相同的原因不再一一赘述。

第三， Scu对 dp模 拟的影响同样取决于 Scu在谱空间中的分布形态以及 dp所在方向。图8 左侧2 列Δdp同样出现了在x 轴两侧变化趋势相反的现象：对照图9a 和图9e 可见，由于 Scu在 dp两侧分布的不对称性，在A、M 点和C、O 点处 dp向 Scu谱值较小的一侧偏转；而在B、N 点上，由于 Scu在 dp两侧对称分布，因此 dp不发生偏转；同样的原理也适用于图8 左侧2 列中的其他方案结果。而对于图8右侧2 列的8 组方案， Scu在 dp两侧出现一正一负的分布形态（图8 中G～I 点对应图9c，图8 中J～L点对应图9d，图8 中S～U点对应图9g以及图8中V～X点对应图9h），因此 dp在整个关注区域中均向谱空间中Scu为负（ Scu谱值较小）的一侧偏转。需要说明的是，在s-1梯度下， Scu对dp的作用效果十分微弱，而 dp的 计算是通过式（13）得到，存在一定的数值不稳定性，因此图8 中的Δdp存在一定的不规律性，但变化趋势仍是明确的。

最后， Scu对 Hs模 拟的影响在浪场空间中存在累积效应，即在波浪传播方向上，上游浪场中Scu使得ΔHs模拟值增加或减少的效果会向下游累积，如图7a、图7i 和图7c、图7f 中，模拟浪场沿波浪传播方向（x 正向）ΔHs逐 渐减小或变大，同理，图7 右侧2 列中，ΔHs在关注区域中沿x 轴向两侧变化幅度增加。且ΔHs/ H˜s的量级为1%。

根据上述分析可知，当流向与流速梯度方向一致或相反时， Scu会使得 Hs的模拟值减小或增大，并且 dp与 流速梯度方向越趋于一致或相反， Scu对 Hs模拟的影响效果越明显。而当流向与流速梯度方向垂直时， Scu对 Hs模 拟结果的影响趋势则与 dp密 切相关（依据 Scu在 dp两 侧谱空间的分布情况）；当Scu在 dp两 侧对称分布时 Scu可出现不改变 Hs模 拟值的情况。 Scu的作用同样可使模拟 dp出现偏转，同样根据 Scu在 dp两 侧谱空间的分布情况， dp总 是向 Scu相对较小的一侧偏转；特别地，流速梯度(∂Ux/∂y)(∂Uy/∂x)＞ 0 会使得 dp逆 时针偏转，而 (∂Ux/∂y)(∂Uy/∂x)＜ 0 使得 dp顺时针偏转。

2.3 10-5 s -1 与 10-4 s -1 梯度量级下 Scu影响效果比较

为使得2 种流速梯度量级下， Scu的作用效果可比，此章节设计了10-4s-1的理想方案，分别采用如图5a 和图5b 所示的流速变化区（关注区）开展。2 种流速梯度下的所有实验均采用相同的驱动风场，风场方向设置为与x 正向成30°夹角，大小20 m/s，且在整个计算区域内一致；在实验过程中，驱动风场同样保持恒定。如此设置的风场可使 dp模拟值即使在25 km×25 km 的小关注区域中也可以与梯度方向有一定的夹角，避免方案c～d、g～h 中 dp两 侧 Scu能量变化相互抵消（如图9c～图9d、图9g～图9h 所示）的情况，导致 Hs无可比性；且避免方案a～b、e～f 中因dp两侧 Scu能量对称（如图9a～图9b、图9e～图9f 所示），导致 dp无变化而出现不可比的情况。在不考虑Scu的作用时，模拟72h后，的关注区域内的和分布情况分别如图10a、图10b 所示，其中颜色表示的 大小，箭头指向方向。由于已知的作用效果与流向无关，因此理想实验仅在方案a～h（共8 组）下开展。

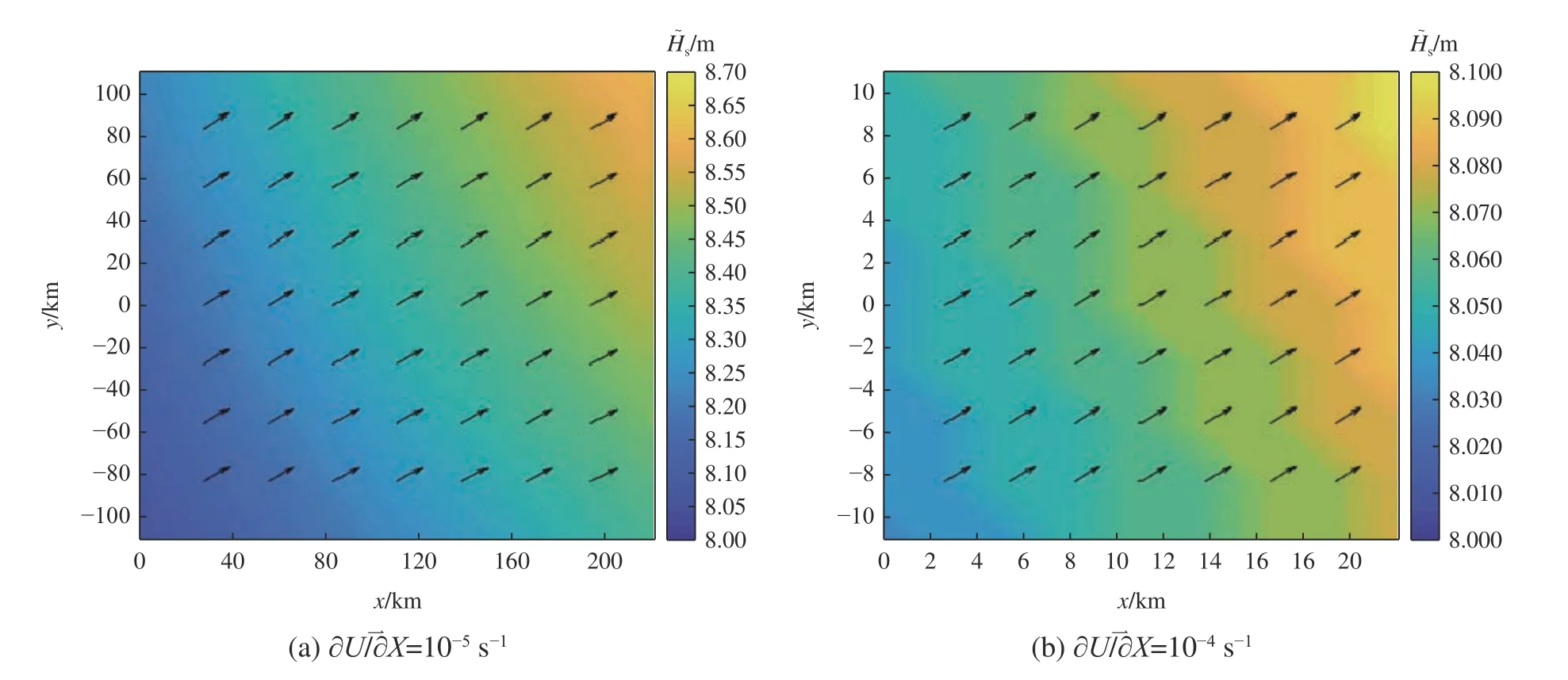
图10 不考虑Scu、在情况下模拟72 h后关注区内和分布Fig.10Significantwave height and spectralpeakdirectio n after72-hour simulation with and excludingScu

图11 模拟72 h 后ΔHs的分布Fig. 11ΔHs distribution in the region of attention after a 72-hour simulation

如图11～图14 所示，相同实验方案中、2 种流速梯度作用下， Scu对 Hs、 dp模拟值的影响趋势相同但程度有所差异。在s-1的 所有实验中，关注区域中ΔHs最高为0.2 m（方案a、e），Δdp最大为1°（方案b、f），而在s-1的 实验中，在 Scu作用下的 Hs模拟值变化最大可达0.35 m（同为方案a、e）， dp模拟值最大变化可达1.6°（同为方案b、f）。由于图11、图13 的关注区域大于图12、图14 的关注区域，因此图11、图13 中的关注区域产生的累积效应更强，且图11、图13 中 以及 的绝对值大小普遍小于图12、图14；由此可ΔHsΔdp知， 对 、 模拟值的影响程度与流速梯度绝对值的大小成正比关系。ScuHsdp

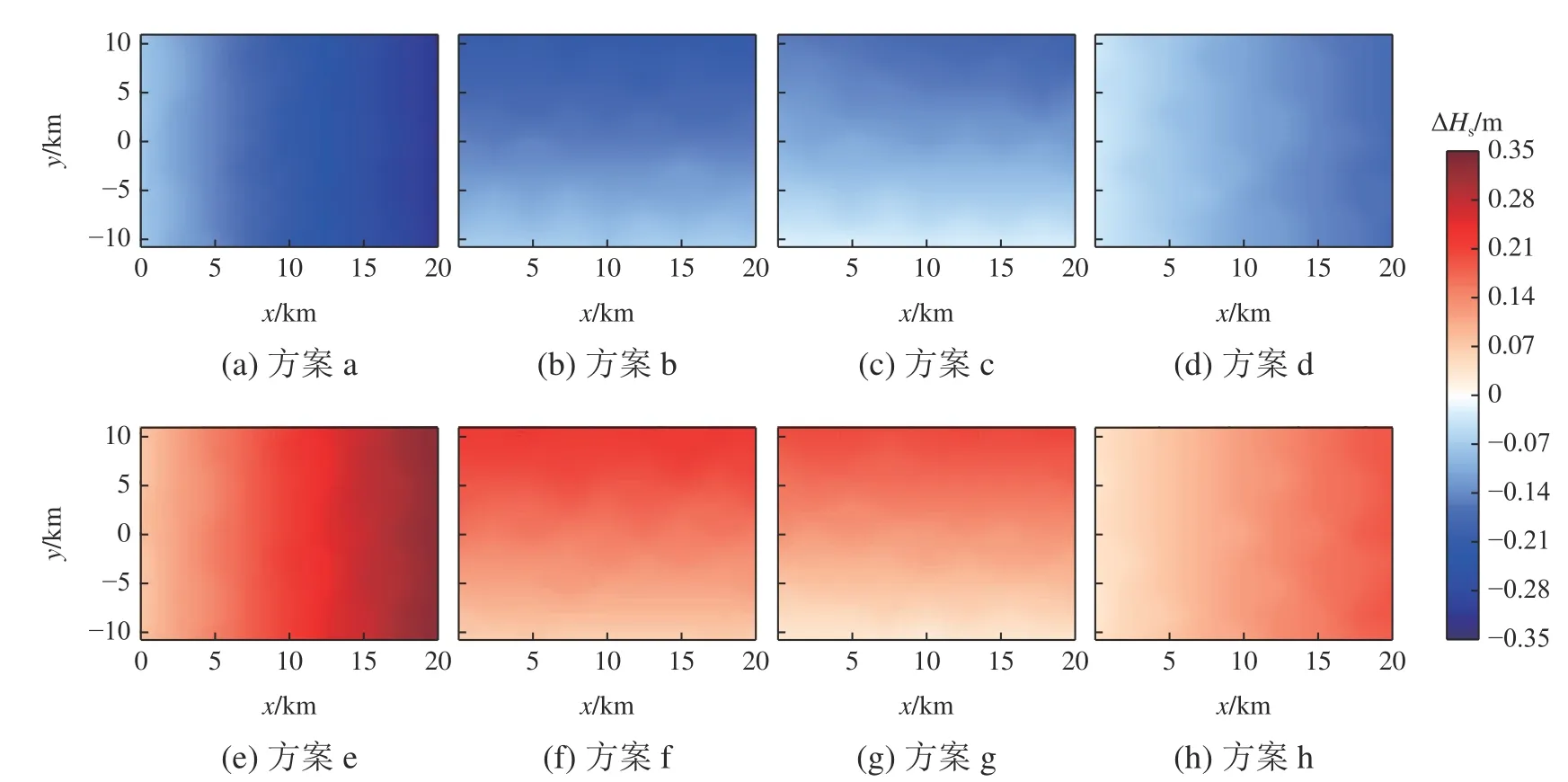
图12 模拟72 h 后ΔHs的分布Fig. 12ΔHs distribution in the region of attention after a 72-hour simulation

图13 模拟72 h 后Δdp的分布Fig. 13Δdpdistributiom in the region of attention after a 72-hour simulation

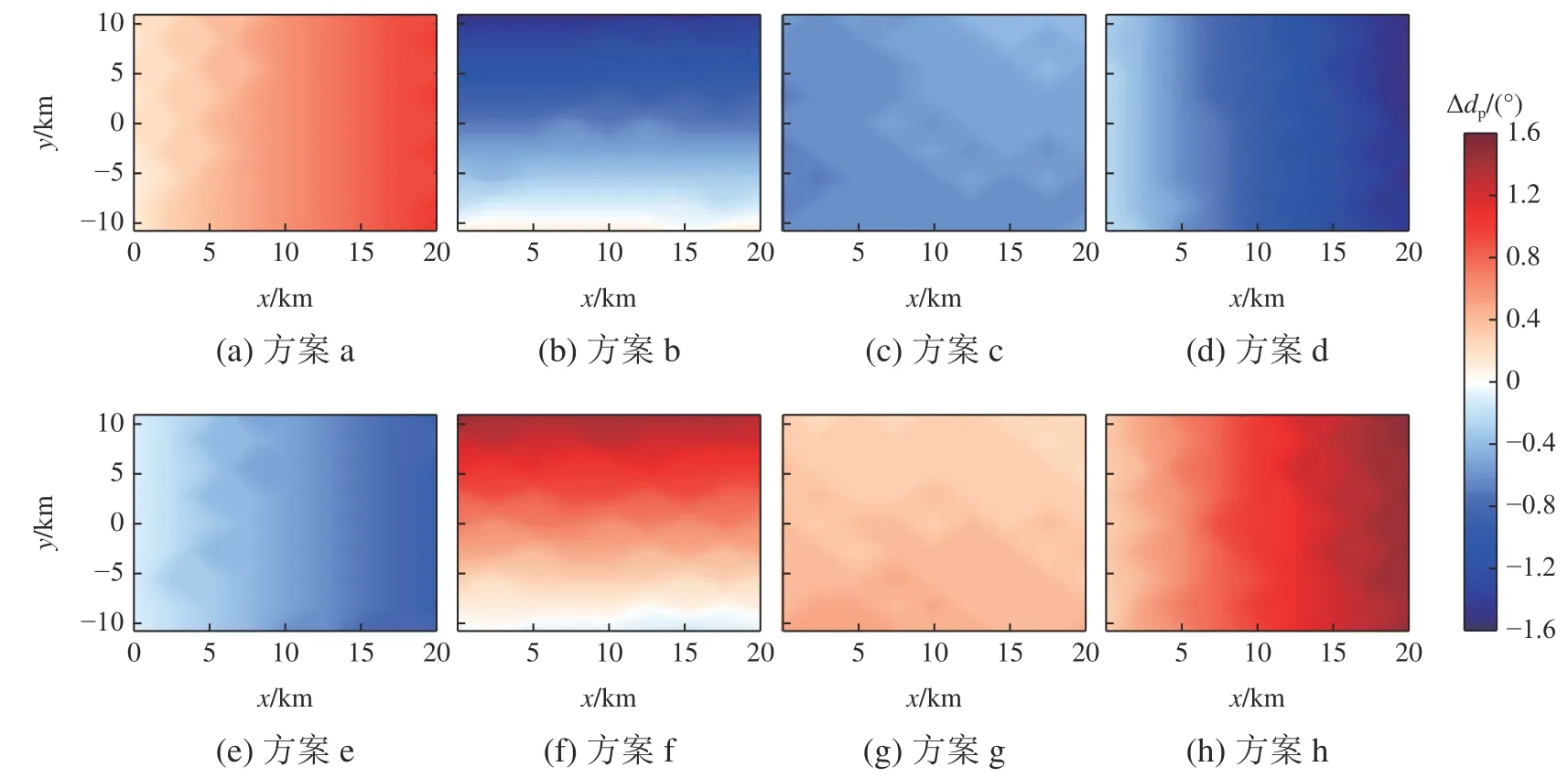
图14 模拟72 h 后Δdp的分布Fig. 14Δdp distribution in the region of attention after a 72-hour simulation

3 结 论

本文系统分析了波-流相互作用源函数[11-13]（ Scu）的特性，并在第三代海浪模式MASNUM-WAM[11-13]的基础上，通过多个理想实验，充分分析了 Scu对 Hs和 dp模拟可能产生的影响，主要结论如下。

1）由于 Scu中包含了参数 cg/c， 因此， Scu对 Hs和 dp模拟的影响效果可因水深及波浪成长状态的不同而发生变化，实验表明：在波浪成长的初期， Scu对波浪模拟的影响较小，而波浪成长得越充分，Scu对波浪场模拟的影响越大；此外，水深越深， Scu的影响效应对波浪成长状态越不敏感。

2） Scu对波浪模拟的影响仅与流速梯度的方向、大小，以及海浪谱的分布形态有关，而与流速的方向、大小无关。

3）当流向与流速梯度方向一致或相反时， Scu会使得模拟 Hs的 模拟值减小或增大；且 dp与流速梯度方向越趋于一致或相反， Scu的影响效果越明显。而当流向与流速梯度方向垂直时， Scu对 Hs模拟结果的影响趋势则与 dp密 切相关，当 Scu在 dp两 侧谱空间的分布对称时， Scu可能对 Hs的模拟无影响。

4） Scu可使 dp模 拟值发生偏转，偏转趋势与 Scu在 dp两 侧谱空间中的分布形态有关，即 dp总 向 Scu相对较小的一侧偏转；特别的，当流向与流速梯度方向垂直时， (∂Ux/∂y)(∂Uy/∂x)＞ 0 会使得 dp逆时针偏转，而(∂Ux/∂y)(∂Uy/∂x)＜0使得 dp顺时针偏转。

5）本文考虑了10-5s-1和1 0-4s-1两种不同量级的流速梯度，但在真实海洋中，尤其是开阔海域中，后者的量级很难达到，因此通常情况下 Scu对 Hs、 dp模拟值的影响非常小；但考虑到涌浪的长距离传播， Scu对 dp的影响仍可能明显改变涌浪的传播形态。