矢量电推进系统的气动-推进耦合模型
夏济宇,周洲,徐德,王正平
西北工业大学 航空学院,西安 710072
随着科技的进步与社会的发展,人们愈发关注低碳发展模式,世界各国相继提出了自己的碳中和目标。在航空界,绿色航空也逐渐得到研究机构与学者们更多的关注[1-2],然而传统的航空燃油发动机在工作方式和效率等方面受到诸多限制,因此更加高效、节能、环保的分布式电推进系统成为了如今的一个研究热点[3-4]。
分布式电推进系统(DEP)由多个螺旋桨或涵道风扇组成,具备实现结构共形设计与气动推进一体化设计的巨大潜能。DEP 通过对机翼表面气流的抽吸,可以有效改善飞机气动特性,欧盟“洁净天空2”计划[5]表明,二维场景下涵道影响区域机翼的最大升力系数甚至可达4.5。基于边界层抽吸(BLI)效应,经过良好设计的DEP 具有更高的推进效率[6],更加符合绿色航空的要求。此外,DEP 的多推进器冗余使飞机具有了更强的容错能力,从而得到更为可靠的安全保障[7]。
正是由于DEP 的众多优点,国内外学者对分布式电推进技术进行了大量的研究。比较著名的方案有美国NASA 的X-57 麦克斯韦试验飞机[8]、Joby S2 飞机,德国Lilium Aviation 公司的Lilium Jet[9]等。Kerho 和Kramer[10]在NASA LEARN 项目资助下,使用计算流体力学和风洞试验方法研究了小型分布式电推进飞行器的推进器对机翼气动性能的影响。法国ONERA 实验室的Hermetz 等[11]设计了2 架小型无人机,一架为三翼面布局,分布式涵道风扇布置于机翼后缘;另一架机翼上置,沿机翼前缘布置分布式涵道风扇。Hermetz 等基于CFD 方法进行二维和三维仿真计算,以研究气动-推进耦合,其中转子采用桨盘模型,在二维仿真中,主要分析了机翼翼型、涵道转子位置和转子直径这几个参数变化带来的影响,在三维仿真中,进行了涵道风扇进排气的详细设计。张阳等[12]研究了分布式涵道风扇喷流对后置机翼的气动性能影响,通过涵道单元/涵道-机翼的地面试验验证了数值计算方法的可靠性和高效性,并进一步对分布式涵道风扇-机翼构型的气动优势进行了分析讨论。张星雨等[13]设计了一套地面测试平台,结合数值模拟方法对分布式电推进技术验证机的气动性能及其气动-推进耦合关系开展了研究,其研究结果表明,涵道对机翼边界层的抽吸效应使得上翼面的气流加速,从而引起升力增加,并且造成气动焦点后移的现象。电涵道作为DEP 的核心,部分学者还针对其气动和推进特性展开研究。Traub[14]对一系列新型空涵道外壳,在改变迎角参数下进行了大量的试验研究。Drela 等[15]开发的DFDC 是一种轴对称涵道风扇分析工具,给定涵道风扇的设计配置,DFDC 可以快速准确预测涵道风扇的力与力矩。Bontempo 和Manna[16]使用非线性半解析模型分析了涵道转子周围的轴对称流场,重点分析了涵道横截面的弧度和厚度对性能的影响。
现有研究已经明确指出,电推进系统的气动和推进之间存在强烈的耦合效应[17],但是传统基于工程经验的气动分析方法无法很好地描述气动-推进耦合效应[18],以CFD 为代表的数值计算方法无法满足飞行动力学与控制系统对于模型的实时计算需求[19]。因此,研究电推进系统的气动-推进耦合效应是当前的重要研究方向,而如何建立快速、精确的气动-推进耦合计算模型是其中亟须解决的关键问题。
在现有文献中,尚未见到适用于电推进系统的气动-推进耦合实时计算模型。本文的目标是,在保证所建立气动-推进耦合模型能描述出系统主要特征与具备实时计算能力的前提下,使模型达到尽可能的高精度。根据电推进系统的特点,本文从涵道推进系统入手,基于理论模型与工程经验模型将涵道总推力与涵道转子推力相关联,得到涵道系统的各截面气流状态;然后基于涵道的气动经验公式且根据涵道桨盘截面速度修正涵道气动模型;接下来,分析如何处理涵道抽吸对机翼气动特性的影响,并建立机翼气动增升模型,此外根据涵道是否倾转分别展开讨论;最后,将所有模型统一至机体坐标系下,完成了气动-推进耦合模型的建立,并且根据CFD 仿真计算验证了气动-推进耦合模型的准确性。本文提出的气动-推进耦合模型具有极快速的计算能力,满足无人机动力学系统与飞行控制系统的实时计算需求,具有工程实用与理论分析价值。
1 研究对象
本文研究对象是类似于Lilium Jet(见图1)的一种矢量电推进系统,研究重点是机翼与电涵道之间的气动-推进效应,该矢量电推进系统仅为DEP 的一部分,由有限长度机翼和位于机翼尾部的单个可倾转电涵道组成。矢量电推进系统中α为机翼迎角,ζ为涵道倾转角度,c、l分别表示机翼与涵道外壳弦长,r2、r、rout分别表示涵道入口截面、桨盘截面、出口截面的半径,A2、A、Aout分别表示涵道入口截面、桨盘截面、出口截面的面积,x2、xout分别表示涵道入口、涵道出口至桨盘截面的距离,如图2 所示。

图1 Lilium Jet 矢量电推进系统[9]Fig.1 Lilium Jet vector electric propulsion system[9]
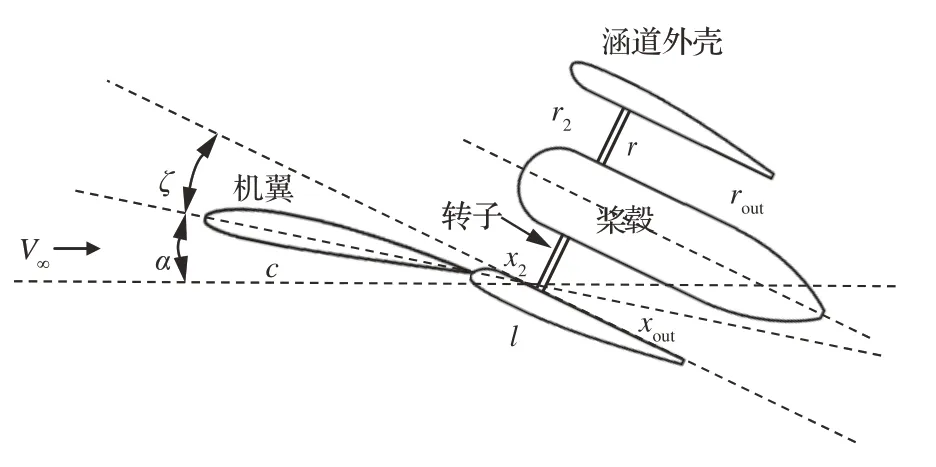
图2 矢量电推进系统参数Fig.2 Parameters of vector electric propulsion system
矢量电推进系统具有如下优势与潜能:①通过推进系统与机翼融合设计,提高推进效率;② 基于电涵道的可倾转特性,无人机能够实现短距/垂直起降;③由于电涵道的尺度无关性,推进系统布局更加灵活;④ 拓展了无人机的操纵方式与能力,可减小甚至取消气动舵面。
矢量电推进系统作为无人机的动力单元,或分布式布置或自由组合,为无人机提供气动升力与推力。建立高效、准确的气动-推进耦合模型有助于降低系统不确定性、提高无人机动力学模型精度,对飞行控制系统响应速度与控制效果的提升也大有裨益。
2 涵道系统模型
涵道系统不仅为无人机提供推力,同时涵道外壳也是气动升力体,因此涵道系统模型包括涵道推进模型与涵道气动模型两部分。
2.1 涵道推进模型
相比于孤立螺旋桨,在来流速度较低时涵道外壳能够额外提供一部分推力,因此涵道系统具有更高的推进效率。目前,关于孤立螺旋桨的研究已经相当完善,但是在涵道系统中,如何准确描述涵道的转子推力与涵道总推力的定量关系还需充分探索。系统典型截面如图3所示。
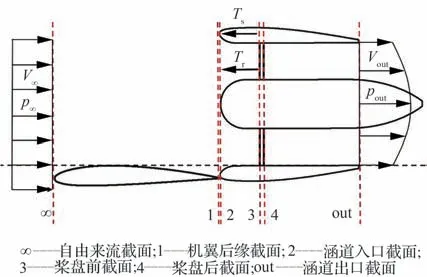
图3 系统典型截面Fig.3 Typical sections of system
为了便于分析,进行矢量电推进系统的典型截面划分,其中下标“∞”表示自由来流截面,“1”表示机翼尾缘截面,“2”“3”“4”分别表示涵道入口、桨盘前与桨盘后截面,“out”表示涵道出口截面。本文涵道形状较为常规,将涵道内部气流视作均匀轴向流动。另外,理想地认为涵道设计良好,在涵道出口处静压恢复至来流静压。
转子的桨盘模型能够准确描述穿过转子以及上下游无黏性区域的流动变化[19],因此其依旧被广泛应用。涵道转子推力的表达式为
涵道系统的总推力T由涵道外壳推力Ts与转子推力Tr共同组成,从上游恒压区至下游涵道出口,基于积分形式的动量方程[20],将涵道系统的总推力表达为
定义关系Ts=CsTr,Cs为涵道外壳的推力比例系数,Cst=1+Cs为涵道的推力增强系数,即T=CstTr,参考文献[21]进行Cst的理论推导。当输入功率为0 W 时,Cst的一阶近似值为
采用线性流体力学方法,将涵道流场分解为关于考虑涵道外壳厚度的均匀流,加上关于通过涵道桨盘的均匀流,以及关于考虑涵道内壁弯曲的均匀流。
首先,基于涵道出口截面中心线的速度,考虑几何参数对于流场流动行为的影响。中心线速度具有4 个分量,其无量纲形式写作
如文献[20,22]所述,使用毕奥-萨伐尔定律进行积分可以确定涵道中心线上沿无量纲距离的诱导速度。令。
转子旋转对于速度的贡献基于半无限涡流圆柱进行建模,忽略尾迹旋转与尾迹收缩。
然后计算涵道内壁弯曲对于出口截面诱导速度为
涵道外壳翼型厚度明显影响桨盘截面速度,但对于出口速度的影响则为
基于中心线速度认为涵道桨盘截面和涵道出口截面质量流守恒,经过代数运算后得
所推导的涵道推力增强系数Cst将涵道设计参数耦合进来,如涵道入口与出口半径、桨盘截面至涵道出口截面的长度,很好地体现了涵道设计特征,使模型参数具有明确物理意义,更为详细的分析可以参考文献[19,21]。
Cst的表达式还揭示了一个现象:在低来流速度与高推力时,涵道外壳的推力增强效应显著;而在高来流速度与低推力时,涵道外壳甚至阻碍气流流动而产生负推力。因此,为了使涵道螺旋桨扬长避短,需要根据实际工作点设计其额定推力、螺旋桨参数与涵道外壳参数。在4.3 节模型验证与分析中也将体现该现象。
涵道拉力与功率系数计算模型早已工程化,基于应用最为广泛的模型将涵道拉力系数与功率系数计算公式写作
拉力系数、功率系数与前进比J=V∞/(nd)分别呈一次与二次函数关系,进一步可得
结合式(5)与式(7)即可在来流条件与涵道转子转速已知情况下,求得涵道总推力与转子推力,进一步结合伯努利方程、动量方程与质量守恒方程计算出涵道系统内外部流场的各截面实时状态:
涵道转子的工作状态将对涵道与机翼的气动力产生影响,2.2 节将根据相应截面的气流状态修正涵道与机翼的空气动力模型。
2.2 涵道气动模型
涵道系统的空气动力主要来自于涵道外壳,涵道外壳一般为某一翼型的旋成体,其特征与环形翼极为相似。Werle[23]通过大量的试验和计算数据验证了一个线性无黏气动力模型的可靠性,此模型可以计算不同迎角下孤立涵道外壳/环形翼(无转子)的升力。
因此当不考虑涵道转子的影响时,即涵道转子输入功率为0 W 时,涵道系统的升力和阻力系数表达式如式(9)和式(11)所示。
涵道气动升力系数公式为
涵道气动阻力系数公式为
式中:e为涵道外壳的奥斯瓦尔德效率因子,当AR=2时,e=1.36,当AR=1时,e=1.25。
进一步,易得涵道升阻力计算公式为
则输入功率为0 W 时,涵道轴向与法向气动力为
当涵道转子工作时,涵道内部气流状态发生变化,参考发动机的处理方法[21],基于涵道桨盘处质量流量差修正涵道外壳法向力:
3 耦合推进系统的机翼增升模型
在工程应用中,一般采用气动导数模型描述机翼的气动力,这种模型在机翼受其他部件影响较少且流场为层流的情况下效果理想。然而,当存在推进系统显著影响机翼气流流动情况时,如何考虑推进系统的耦合效应是一个亟需解决的关键问题,并且耦合效应的处理方式将直接影响机翼气动力模型的精度。
针对本文研究的推进系统置于机翼尾缘的气动-推进耦合系统,推进系统会对机翼表面气流产生抽吸作用,因此会对机翼的气动力产生诱导效应。针对本文研究的此类气动-推进耦合系统,涵道螺旋桨对机翼下表面气流的影响作用可以忽略,因此主要考虑涵道对于机翼上表面气流的诱导效应。以下标ou 表示机翼在自由来流流场中的上表面状态,od 表示下表面状态,Vi则表示诱导效应下机翼上表面速度。
为了描述这种诱导效应,本文将机翼上表面速度增量直观地表示为ΔVi=Vi−Vou=g(V∞,V1),即速度增量是关于自由来流与机翼尾缘气流的非线性函数。机翼尾缘气流与自由来流和涵道入流直接相关,同时涵道入流条件依赖于自由来流与涵道推力,因此本质上来说,流场在机翼上表面的发展主要受自由来流与涵道推力影响。机翼尾缘速度的求解分为涵道倾转角度为0°与涵道倾转角度不为0°这2 种情况,将在3.1 与3.2 节分别讨论。
原始机翼升力可由机翼上下表面压差积分而得
式中:w为机翼展长。
机翼升力由受自由来流影响的基础升力与受涵道诱导影响的升力增量共同组成,即L=Lo+ΔL。同理,升力增量可由机翼上表面压力增量积分而得
再将dl进行无量纲处理得
则机翼受推进系统诱导后的总升力系数表示为
除此之外,还必须考虑诱导效应对于机翼俯仰力矩系数的改变,俯仰力矩增量系数公式为
则总俯仰力矩系数表达式为
式中:Cmo为机翼原始俯仰力矩系数。
3.1 涵道倾转角度为0°
当涵道倾转角度为0°时,“1”截面与“2”截面重合,即V1=V2,p1=p2。因此,可以直接将涵道入流状态作为机翼尾缘状态。在自由来流与涵道推力已知条件下,由式(5)得到转子推力与涵道总推力的关系Tr=T/Cst,由式(8)得V1=,再结合式(17)~式(23)的推导,即可求解出涵道倾转角度为0°时,机翼的诱导速度增量与气动系数修正。
值得注意的是,涵道的存在并非一直增强机翼上表面流场流动。实际上,当来流速度较低、涵道推力较大时,涵道抽吸机翼上表面气流,使气流速度增大;当来流速度较高、涵道推力较小时,涵道反而阻碍机翼上表面气流流动,使气流速度减小。
3.2 涵道倾转角度不为0°
首先,涵道倾转所产生的效果相当于增大机翼弯度,因此类比常规气动舵面,将涵道倾转角度作为机翼气动导数变量,即CL=CLo+CΔL+CLζζ。另外,当涵道倾转角度不为0°时,机翼尾缘截面与涵道入口截面不再重合,因此需要建立由涵道入口气流状态逆推机翼尾缘气流状态的公式。
与3.1 节相同,涵道入口气流速度可以在自由来流与涵道推力已知的情况下推导出来。然后,为了在自由来流速度V∞与涵道入流速度V2已知的情况下进一步推导出机翼尾缘截面的气流速度V1,本文借鉴圆柱绕流公式描述这种气流诱导与气流偏转。将涵道与机翼连接点作为虚拟圆柱圆心,以涵道入口半径为虚拟圆柱半径,并且将机翼尾缘至涵道入口沿中心线的速度,即沿虚拟圆柱的圆周速度,作为相应截面的参考速度。
无环量的圆柱绕流可以用直匀流与偶极子叠加获得[24]。合成势流的速度势函数为
则合成速度场为
由于驻点位于x轴上,且在驻点处yA=0,可得偶极子强度为。
在极坐标系下,速度势函数与速度场可表达为
本文基于实际情况,提出双圆柱绕流(如图4所示)假设。

图4 双圆柱绕流示意图Fig.4 Schematic diagram double circular cylinder wake
第1 次圆柱绕流:将自由来流V∞作为基础入流,得到绕虚拟圆柱ζ角度的涵道入口基础速度[V2]0。然后将真实的涵道入口速度V2与[V2]0作差,得到涵道诱导速度增量[V2]1=V2−[V2]0。第2 次圆柱绕流:将涵道诱导速度增量[V2]1作为反向入流,得到反向绕虚拟圆柱ζ角度的机翼尾缘诱导速度增量[V1]1。因此,在自由来流与涵道诱导的影响之下,机翼尾缘截面的速度为V1=V∞+[V1]1。
必须注意的一点是,不同于一般圆柱绕流,本文中的入流与反向入流所处的位置为虚拟圆柱的90°位置而非圆柱正前方(0°位置),因此在进行上述速度场计算时,需要进行速度数值与角度的变换。综上,即可求解出当涵道倾转角度不为0°时,机翼的诱导速度增量与气动系数修正。
4 气动-推进耦合模型
4.1 气动-推进耦合模型综合
为了体现气动-推进耦合模型的实际应用价值,而不仅仅是零散的相关模型,本节将文中所有模型综合至同一坐标系下,采用相同的状态变量进行表达。
根据第2 节和第3 节的分析,矢量电推进系统中各模型分别将部分输入变量作为已知变量,为了统一各模型的输入输出,实现模型的一体化效果,需要明确各模型分别强烈依赖何种变量,各模型间变量的相互关系是怎样的。首先,涵道推进模型依赖于自由来流与涵道转子转速,机翼迎角与涵道倾角的变化也会改变轴向入流速度;其次,涵道迎角由机翼迎角与涵道倾转角叠加而来,即αd=α+ζ,涵道转子的工作状态直接影响涵道气动力;另外,由于涵道对机翼上表面气流产生抽吸作用,改变了上表面气流流速从而导致气压分布变化,而涵道倾转一方面调整了抽吸作用的效果,另一方面相当于改变了机翼弯度。气动-推进耦合模型如图5 所示。
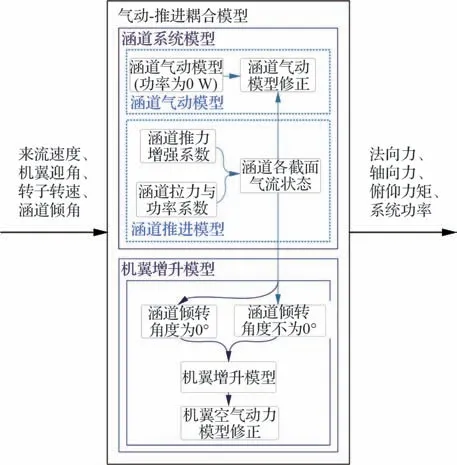
图5 气动-推进耦合模型示意图Fig.5 Schematic diagram of aerodynamic/propulsion coupling model
因此,将涵道推进模型与机翼增升模型中涵道推力与涵道入口截面气流状态统一,将涵道推进模型与涵道气动模型中涵道迎角与涵道桨盘截面气流状态统一,并且涵道输入功率即为系统功率。综上,建立机体坐标系下矢量电推进系统的气动-推进耦合模型为
在气动-推进耦合模型中,自由来流速度V∞、机翼迎角α、转子转速n与涵道倾角ζ为输入变量,系统法向力(升力为主)、轴向力(推力为主)、俯仰力矩、系统功率为输出变量,机翼翼型、弦长、涵道各截面半径、长度、桨盘位置以及涵道转子桨叶参数为系统设计参数。
4.2 气动-推进耦合模型适用性分析
气动推进-耦合模型的建立主要涉及以下4 点假设与简化:①气流不可压缩假设;②假设涵道外壳不发生流动分离,涵道入口不发生流动畸变;③简化涵道内部流场为直匀流,忽略出流的尾迹旋转与收缩;④简化机翼的影响作用,忽略机翼对于涵道的影响。
所研究矢量电推进系统的涵道直径为150 mm,基于气流不可压缩假设,转子桨尖马赫数约束为Matip≤0.3,因此其最大转速为220 r/s,最大功率为1 950 W;涵道实物原型的额定输入电压为58.8 V,电机型号为5020 −KV230。
涵道倾角过大,一方面可能导致外壁面出现流动分离现象;另一方面,在来流速度也较大时,可能还会在涵道入口出现流动畸变现象。因此,当倾转角度小于涵道外壳流动分离倾角与涵道入口流动畸变倾角时,能够保证模型具有较高精度,具体的倾角边界需要根据实际情况确定。
矢量电推进系统中,不仅涵道抽吸机翼上表面气流从而改变流场流动,机翼也会影响涵道的入流条件。为了分析机翼对于涵道的耦合影响,基于CFD 分别计算了孤立涵道与带机翼涵道2 种构型下涵道的推力增强系数Cst,其中机翼迎角、涵道倾角均为0°,来流速度沿涵道轴向。
表1 给出了孤立涵道与带机翼涵道的推力增强系数对比,在当前计算工况下,2 种构型数值极其接近,(结合式(5))说明涵道出流速度基本不变,进一步(结合式(8))说明涵道入流速度基本不变,表明机翼对涵道流场流量影响很小,甚至可以忽略。因此本文暂时忽略机翼对于涵道的影响。
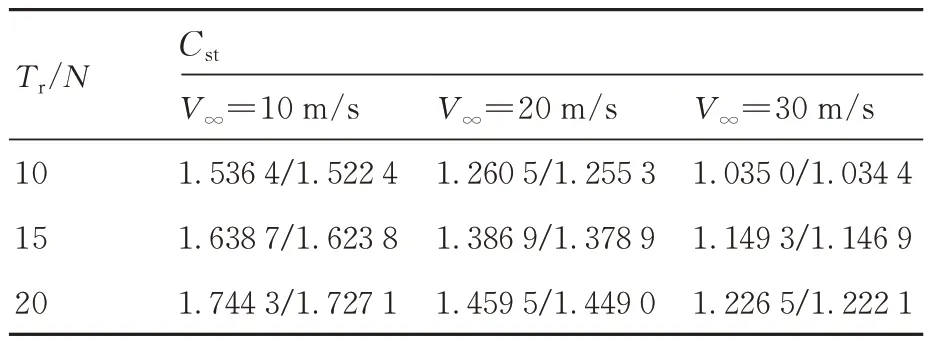
表1 孤立涵道与带机翼涵道的推力增强系数Cst 对比Table 1 Comparison of Cst between isolated duct and duct system with wing
4.3 气动-推进耦合模型验证与分析
为了验证本文矢量电推进系统的气动-推进耦合模型的准确性,基于CFD 方法开展了一系列仿真计算。计算状态选取高度为海拔500 m,雷诺数Re=0.46×106(基于平均气动弦长),力矩参考点取在机翼1/4 弦长处,采用结构化网格对计算域进行离散,网格量约800 万,采用雷诺平均Navier-Stokes(RANS)方程进行流场数值求解,湍流模型采用SST(Shear Stress Transport)模型,基于SIMPLE 压力-速度耦合求解器,空间离散方法为二阶迎风(Second Order Upwind)格式,时间推进采用一阶隐式(First Order Implicit)方程,为了减弱机翼三维效应的影响,将机翼延长至足够长,仅取中间翼段作为研究区域。CFD计算物面网格如图6 所示,分别为涵道倾转角度为0°、30°、60°这3 种状态。
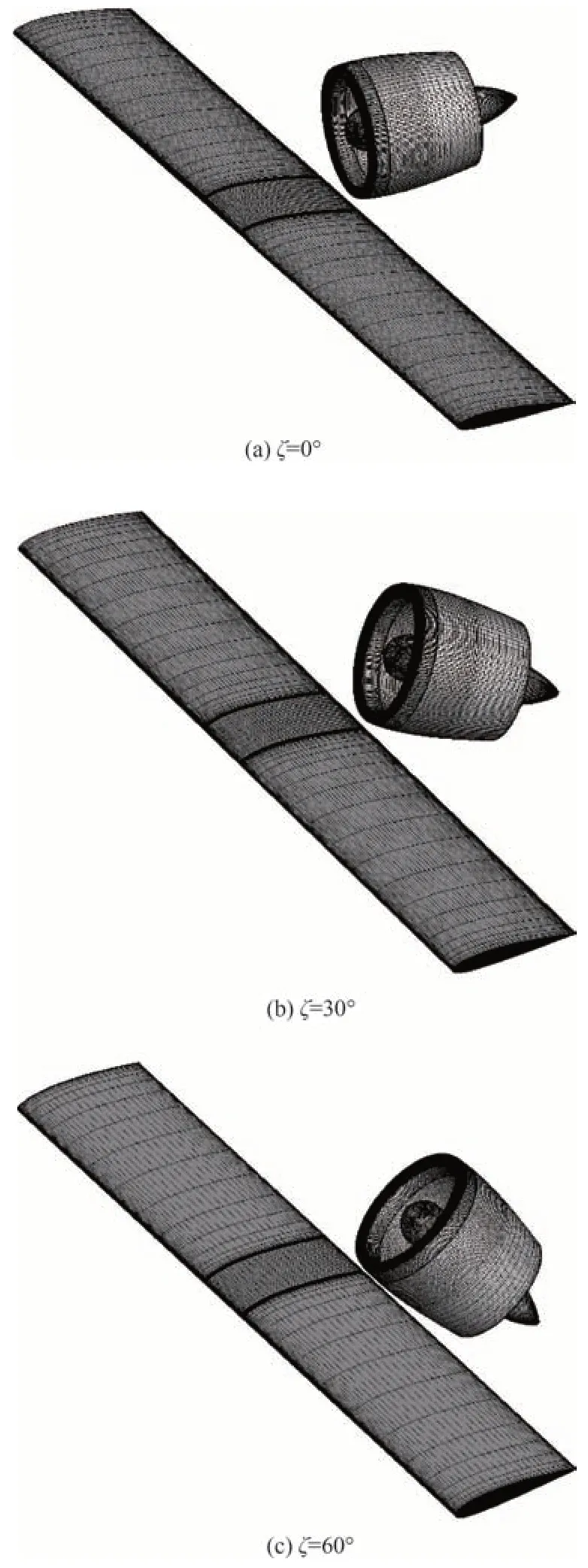
图6 CFD 计算物面网格Fig.6 Surface grid for CFD simulation
矢量电推进系统作为一个涉及大量状态变量与设计参数的系统,其影响因素众多,变化规律复杂,为了更加清晰地了解关键变量对气动-推进耦合模型的非线性影响,文中暂以α=0°展开研究。这是因为迎角一般处于较小的变化范围,且对于机翼而言其影响效果偏线性,对涵道而言迎角相比于涵道倾转角是一个小量,因此,本文更关注来流速度、涵道转子转速与涵道倾转角度的变化对系统带来的影响。
在图7~图10 中,“APCM”表示根据本文所提出的气动-推进耦合模型的快速计算结果(每个计算点均在100 ms 以内),“CFD”表示CFD 数值计算结果(每个计算点约6 h)。为了简化表达,下文以APCM 代表气动-推进耦合模型,另外,下标“vep”表示矢量电推进系统,下标“w”表示机翼,V∞表示计算状态来流速度,ζ表示计算状态涵道倾转角度。
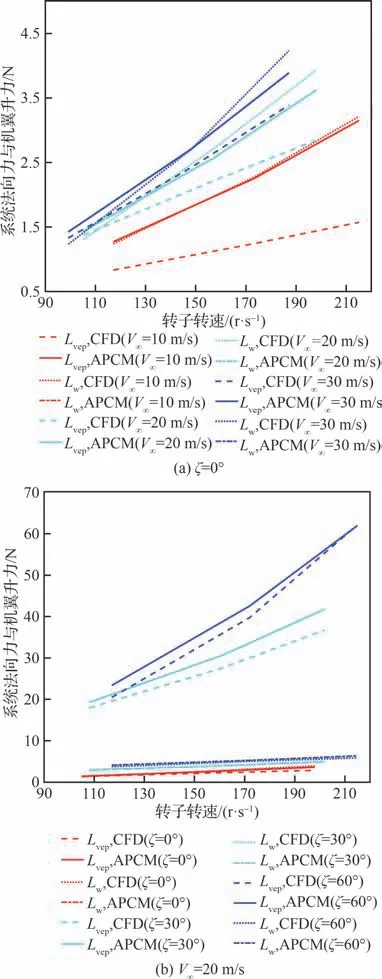
图7 系统法向力与机翼升力曲线Fig.7 System normal force and wing lift curves
当涵道倾转角度为0°时,根据APCM 计算的涵道气动升力为0,机翼气动升力即为系统法向力,因此在图7(a)中,APCM 的Lvep与Lw重合。APCM 对于机翼气动升力的计算结果与CFD 相互吻合,表明本文方法非常准确地预测出涵道抽吸所引起的机翼增升效果。然而由于APCM 理想化地认为涵道推力始终沿轴向,因此在系统法向力计算中产生较大误差。当涵道倾转角度不为0°时,无论是机翼升力还是系统法向力,APCM 与CFD 计算结果均吻合良好,误差大约控制在10%以内,这表明在APCM 具有良好预测机翼增升效果能力的同时,3.2 节中所提出的双圆柱绕流假设是合理且准确的。
在涵道倾转角度为0°与不为0°这2 种情况下,APCM 中机翼俯仰力矩的计算都很贴近CFD 计算结果。然而在图8(a)中,APCM 在大来流速度条件下对系统俯仰力矩的预测,相比于小来流速度条件下更准。这是由于机翼处于涵道下侧,限制了下侧气流的流入,因此更多的气流增量来自于涵道上方,从而导致入流方向发生偏移不再沿涵道轴向(APCM 假设涵道入流为直匀流),在小来流速度下涵道入流不对称现象更加严重,因此误差更大。APCM 中矢量电推进系统俯仰力矩误差与法向力误差产生的原因均来源于此。在图8(b)中,较大的倾转角度工况始终存在较为明显的系统俯仰力矩误差,此现象的原因还跟涵道气动模型误差有关。当涵道倾转角度过大时,涵道作为一个气动升力体已然失速,其气动焦心移动,因此无论涵道转子转速高或低,计算误差均较为明显。在图8(a)与图8(b)中还出现了一个相近的现象:即随转子转速的增大,机翼低头力矩不再为0 N·m 且持续增大,这表明涵道抽吸引起了机翼焦心后移。

图8 系统与机翼俯仰力矩曲线Fig.8 Pitching moment curves of system and wing
如图9(a)所示,APCM 关于系统轴向力的计算结果与CFD 趋势一致,尤其是当来流速度较大时,二者计算结果相差无几。随涵道倾转角度增大,系统轴向力逐渐减小(见图9(b)),这并不代表涵道推力减小,而是表示涵道倾转导致推力在机体坐标系下轴向分量减小。对于系统法向力与轴向力的精准计算体现了APCM 的可靠性,因此这种基于理论模型与工程经验模型相结合的建模方式,不仅在计算速度上远远优于以CFD 为代表的数值计算方法,在计算精度上也并未牺牲过多。

图9 系统轴向力曲线Fig.9 Axial force curves of system
APCM 不仅能够展示最终的输出变量,其还能展现系统中的各子模块的计算结果。在图10(a)与图10(b)中,实线表示了系统功率P,其余曲线分别表示涵道推力T、涵道转子推力Tr与涵道外壳推力Ts。根据图10(a),可以得出同一来流速度下,转速越高,涵道外壳推力占总推力比重越大;而同一转速下,来流速度越低,涵道外壳推力占总推力比重越大。涵道外壳推力占总推力比重越大,说明涵道增推效果越明显;反之,在大来流速度小涵道推力下,涵道外壳甚至提供负推力的效果,这是实际飞行中不希望出现的情况。因此,针对飞机巡航速度进行涵道的选型与优化设计是非常有必要的。在图10(b)中,随涵道倾转角度的增大,涵道外壳推力占总推力的比重有所上升,这是由于在涵道入口气流未发生畸变的前提下,涵道相对来流角度越大,来流沿涵道轴向的速度分量越小,从而使涵道增推效应增强,此现象与本文对图10(a)的分析结果相符。另外,涵道推力与转子转速呈二次函数关系,而涵道功率(系统功率)与转子转速呈三次函数关系,因此对于单一涵道而言,为了获取较大的涵道推力需要付出更大的系统功率,这也恰恰证明了分布式电推进系统的优势,通过分布式多动力装置布局,能够有效降低系统功耗、实现能量的最优配置。
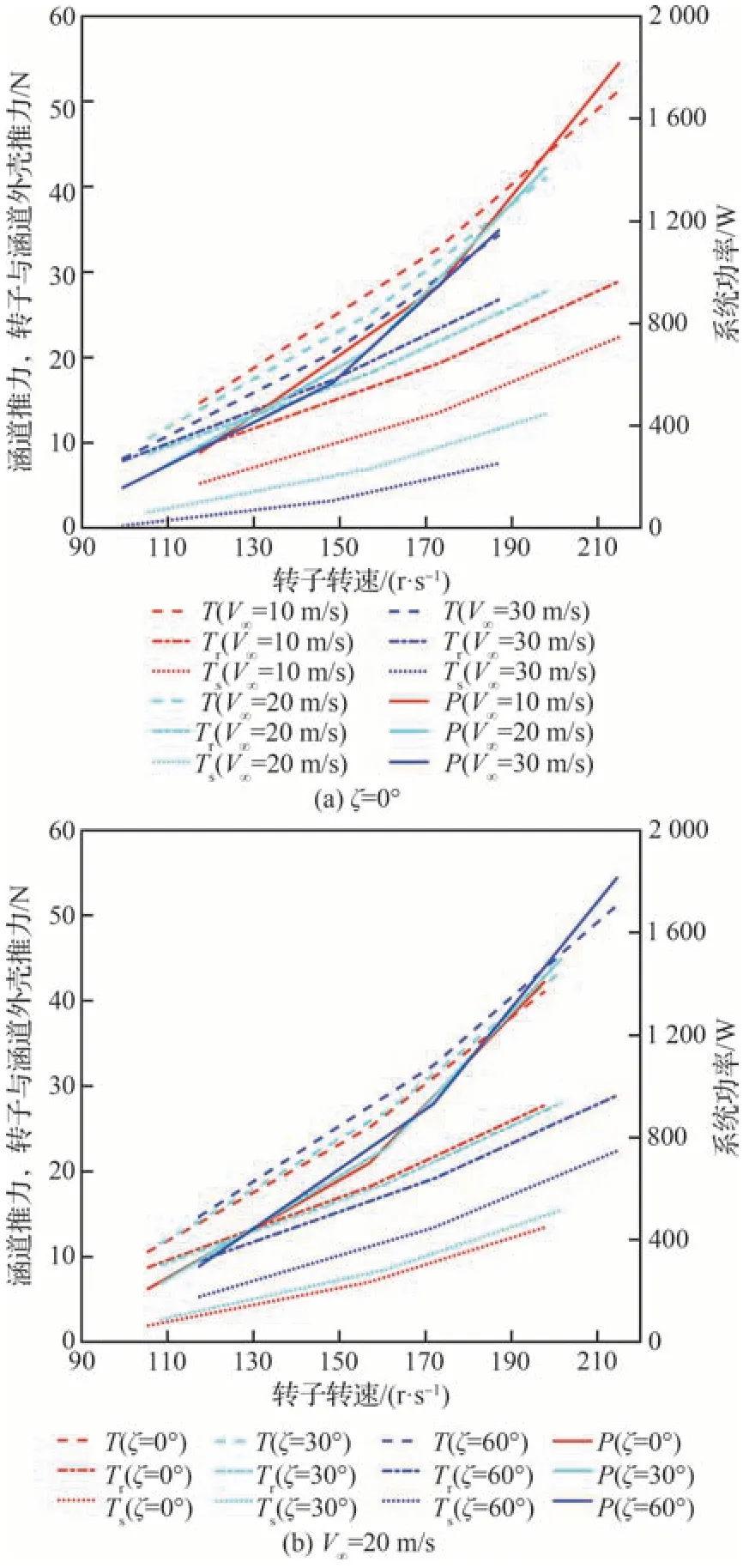
图10 涵道推力与系统功率Fig.10 Pulling force of ducted fan and system power
5 结论
1)本文所提出的矢量电推进系统的气动-推进耦合模型具有实时计算能力,能在极短时间(100 ms)内根据系统输入计算出可靠的输出结果,满足无人机动力学系统与飞行控制系统的实时计算需求,如果通过CFD 数值计算方法往往需要数小时才能完成。
2)气动-推进耦合模型具有描述涵道转子推力与涵道总推力之间定量关系的能力(即随飞行速度减小与转子转速的增大,涵道转子推力占比减小,涵道外壳推力占比增大),可以准确预测涵道各截面气流状态,从而有效修正涵道气动模型与机翼增升模型。
3)气动-推进耦合模型能够准确地估算机翼气动增升效果,针对涵道倾转角度不为0°的情况,本文提出的双圆柱绕流假设可以很好地描述气流诱导与偏转效果。
4)本文主要研究了来流速度、涵道转子转速、倾转角度与迎角对气动-推进耦合模型的影响效果。除了上述分析,还发现了涵道入流方向偏移与机翼焦心后移等现象,为后续研究的展开提供了很好的切入点。在后续研究中,将考虑更多系统设计参数如机翼特征参数,并且进一步研究分布式电推进系统动力单元间气动干扰特性以及布局设计。

